Ambiguity resolution combined with multiple constellations and multiple frequencies proves very effective in reducing Precise Point Positioning convergence time. Such a solution with a 30° mask has a shorter convergence than a float multi-GNSS solution without any obstructions, despite the latter using more satellites.
Precise Point Positioning’s (PPP’s) level of performance is approximately an order of magnitude lower than that of real-time kinematic (RTK), and solutions have a relatively long initial position solution convergence, requiring tens of minutes for a precision of a few centimeters. Among research methods to reduce PPP initial convergence time, ambiguity resolution (AR) has proved effective.
AR takes advantage of additional information that is not used in the classic PPP model: the integer nature of the ambiguities. Indeed, in the classic PPP model, ambiguities are affected by various biases, which make them lose their integer nature. In AR, the biases are extracted from the ambiguities, which are fixed to integers after being estimated as float values. When this process is done correctly, it greatly reduces the convergence time as it eliminates the need to wait for the ambiguities to converge to an integer and can directly fix them to the correct integer.
PPP-AR requires the additional estimation of satellite phase biases, which can be estimated with already-existing ground stations. This makes the results in this article promising as they are achieved without any additional infrastructure, nor any assumption on the density and distribution of the ground infrastructure that is used to generate the necessary phase biases.
The benefit of dual-frequency AR to PPP has been extensively studied and there are clear improvements that come with AR, both in terms of convergence time and accuracy. Most research has focused on the performance of PPP-AR in optimal scenarios (i.e., static geodetic stations, and open skies) to quantify PPP-AR performance. In this article, we focus on the performance of PPP-AR in obstructed environments.
We assess PPP-AR performance in environments such as urban canyons, where many applications seek to improve navigation solutions, and study the benefit of performing AR compared to processing more satellites. Secondly, we study the relevance of AR in a context where tens of satellites from different constellations can be processed simultaneously, as well as the necessity of multi-GNSS processing in a context where AR has proved to improve the PPP performance. As more satellites are launched, will adding satellites keep improving the positioning solution, or is there a limit and, therefore, a necessity to turn to AR as a tool to further improve the PPP performance?
Theoretical Background
Our dual-frequency AR model is based on an uncombined formulation of a Decoupled Clock Model (DCM). In this article, uncombined refers to not forming linear combinations of the measurements, but rather use the raw measurements on each frequency. The model is based on the assumption that the code and phase measurements are not synchronized to the same level of precision and it, therefore, decouples the receiver clocks into a code clock and a phase clock. Doing so removes the datum in the phase measurements from the receiver clock. To restore the phase datum, one satellite is chosen as a reference satellite and its ambiguities are set to arbitrary integer values. This process is referred to as implicit differencing, as all the ambiguities are made relative to the reference satellite without performing explicit between satellite differencing.
All receiver equipment biases and receiver clocks are constellation dependent. Their values are different from one constellation to another due to the presence of inter-system time biases, as well as the constellations being processed by different processing units in the receivers. This situation means that there needs to be as many sets of receiver clocks and receiver biases as there are constellations being processed.
Data and Processing Strategy
To perform the necessary tests and assess the performances of the float and fixed solutions for different constellation combinations and levels of obstructions, a network of 39 worldwide IGS stations was used. The stations were chosen arbitrarily, as long as they provide observations from the four global constellations. They were processed on 7 days between DoY 60 and DoY 66, 2019. The datasets were split into 3-hour sessions, producing over 2000 3-hour-long datasets in total. Figure 1 shows the distribution of the utilized stations. Observations were processed in uncombined mode with ambiguities on both primary frequencies being fixed for GPS (G), Galileo (E) and BeiDou (C). GLONASS (R) was also included in the processing but without ambiguity resolution, as its frequency-division, multiple-access (FDMA) signals make AR challenging.
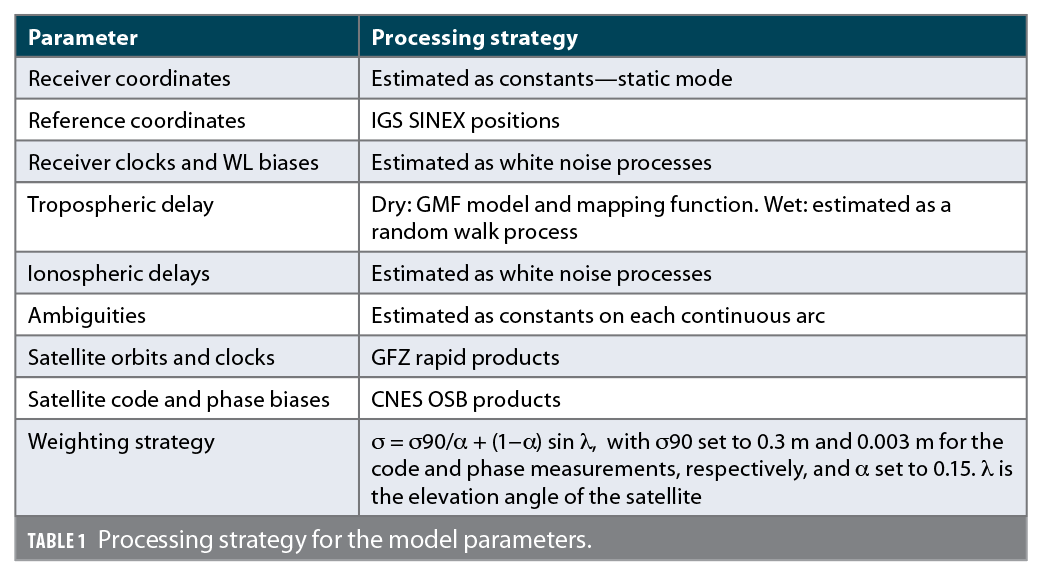
Table 1 shows the processing strategy that was adopted for the different parameters of the model. Besides the estimated parameters, external corrections are used. The satellite code and phase biases, vital for successful PPP-AR, have been corrected for using the CNES Observable-specific Signal Biases (OSB). These biases are provided and applied at the observable level, and they do not require prior knowledge of the method that was used to estimate them on the network side. The OSBs are used together with the GFZ rapid orbits and clocks to maintain compatibility. Both the satellite Phase Center Offset (PCO) and the Phase Center Variation (PCV) are corrected for using the IGS ANTEX file. Other corrections, such as phase wind-up, relativistic effect and Earth rotation are also corrected for following the IERS convention.
The LAMBDA method is used to fix the ambiguities to integer values. First, the float uncombined ambiguities are estimated in a sequential least squares filter. The float ambiguities, along with their covariances, are transformed into narrowlane and widelane ambiguities before being fed to the LAMBDA function. The transformation is optional as the decorrelation step in the LAMBDA method is able to determine the optimal combinations to ensure a high probability of correct fixing. Once the ambiguities are fixed by LAMBDA, they are then used to update the state terms such as the receiver position.
For regular processing without any obstructions, an elevation angle cut-off of 10° is chosen in order to remove satellites with lower measurement quality. Additionally, an elevation angle-dependent weighting scheme is used as highlighted in Table 1. The values that are used for the elevation angle-dependent weighting scheme highlighted in Table 1 were estimated based on a residual analysis of IGS quality data. The obstructions in this paper were simulated by increasing the elevation angle threshold from 10° to 40° in steps of 10°. Although this method of obstruction is not wholly realistic, the main reason behind using it is to increase the Position Dilution of Precision (PDOP) in order to assess how the PDOP affects the PPP position solution both with and without AR.
AR Importance in Multi-GNSS Context
Three constellation combinations are looked into and they are processed both with AR and without AR. The constellation combinations are GPS-only (G), GPS and GLONASS (GR), and GPS, GLONASS, Galileo and BeiDou (GREC). This is to limit the number of solutions as each constellation combination comes with two solutions (float and fixed).
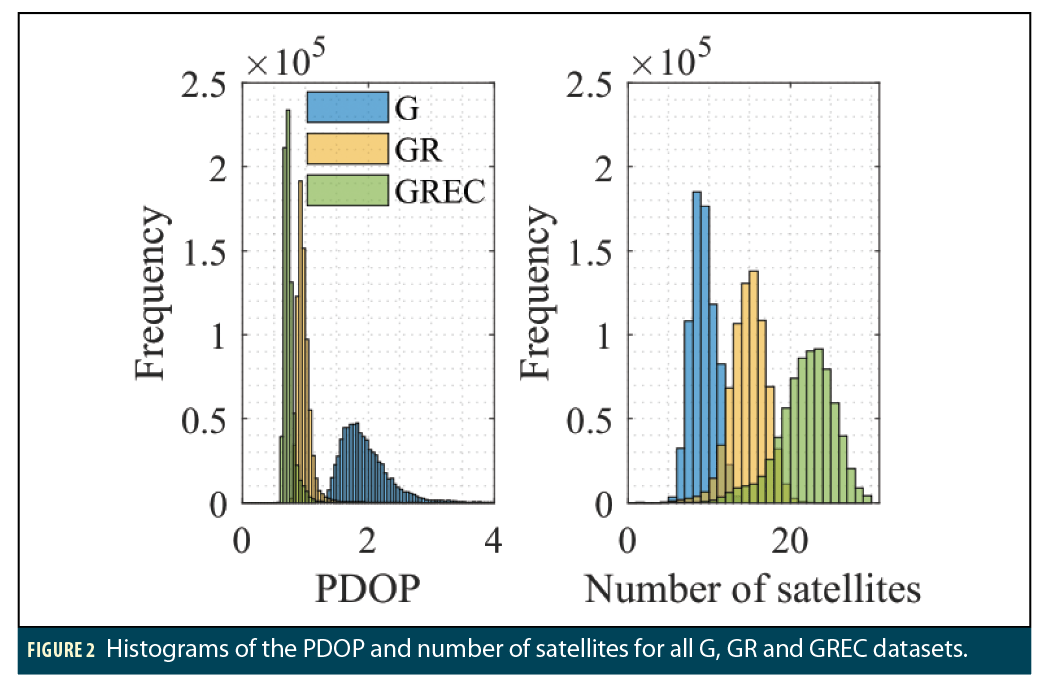
To analyze the impact of the constellation combination on the PDOP and number of satellites, Figure 2 highlights the distribution of the PDOP and the number of satellites for the three chosen constellation combinations. The histograms are generated based on every epoch for all the processed datasets. The bin sizes for the PDOP and number of satellites histograms are 0.05 and 1, respectively.
It is clear from Figure 2 that, as expected, the number of processed satellites increases with the increase in the number of constellations. The average number of satellites in G, GR and GREC is 9, 14 and 22 satellites, respectively. It is interesting to note that the average PDOP for the GREC combination, 0.74, is relatively close to the average PDOP for the GR combination, 0.99, as opposed to the big improvement that adding GLONASS brings to the GPS PDOP of 1.97. This relatively small improvement is despite the fact that adding Galileo and BeiDou to the GR combination adds 7 satellites on average to the positioning solution. The possible reason behind this PDOP behavior is that the satellite geometry from the GR combination is already very good, which means that adding more satellites only improves the satellite geometry slightly, leading to relatively close PDOP—the law of diminishing returns.
On the other hand, the GPS-only configurations have an average PDOP of 1.97, which means that the satellite geometry can be improved to a value closer to 1 through the inclusion of more satellites, i.e., GLONASS.
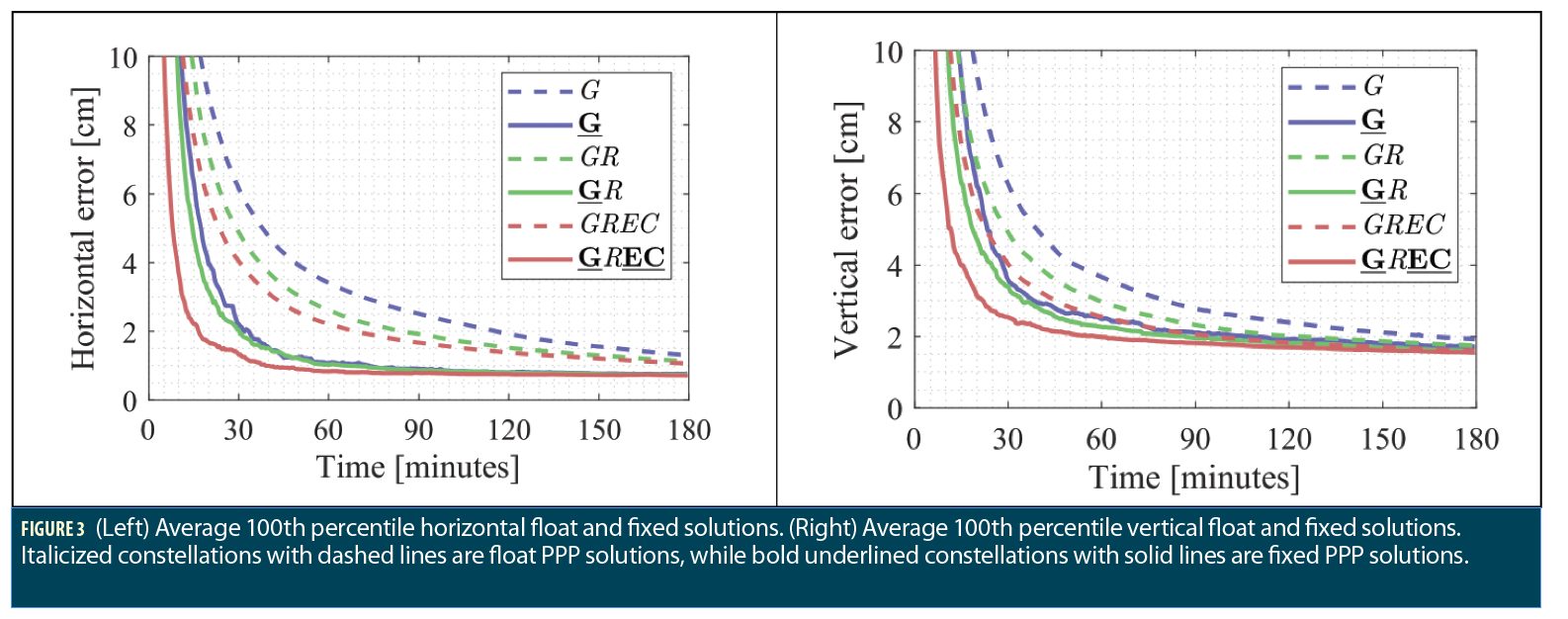
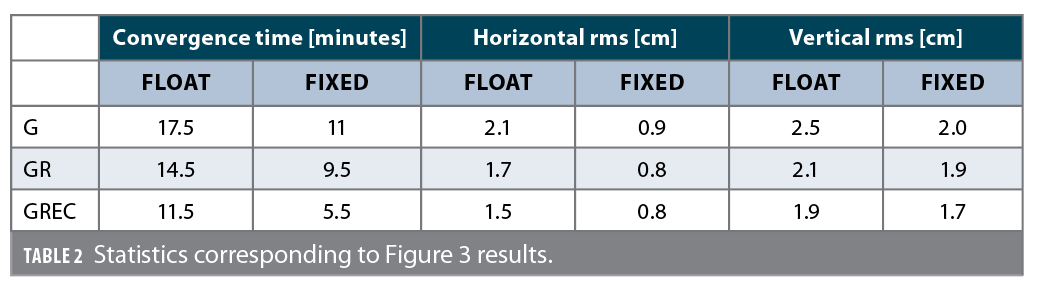
The impact of the PDOP on the PPP solutions can be seen in Figure 3. The figure shows the 100-percentile average based on all datasets for the different constellation combinations. The dashed graph lines represent the float solutions and the solid ones are their fixed counterparts. Table 2 contains the convergence time and rms for each graph in Figure 3. The convergence time is defined as the time it takes for the solution to settle below 10 cm horizontal error or the time at which the horizontal error graph line appears in the figure. The horizontal and vertical rms are computed between minutes 60 and 180 to assess the final accuracies after convergence.
Looking at both Table 2 and Figure 3, it is obvious that AR has a significant impact on solution convergence and accuracy, regardless of the constellation combination. The fixed solution consistently converges faster than the float one and is able to reach higher accuracies. It is interesting to notice that the fixed solutions with fewer constellations can converge faster than float solutions with more constellations. For instance, the fixed G solution converges 3.5 minutes faster than the GR float solution and is able to reach 49% better horizontal accuracies, respectively, even though GLONASS adds an average of 6 additional satellites. The same conclusion holds for the fixed GR solution compared to the float GREC solution. It is worth noting that, in this case, even the GPS- only fixed solution converges half a minute faster than the full float GREC solution, even though the latter has 13 more visible satellites and over half the PDOP of the former. The horizontal accuracies are also smaller in the fixed GPS solution, 0.9 cm, compared to all the float solutions, 2.1 cm, 1.7 cm and 1.5 cm. However, the latter conclusion does not hold all the time, as these results are based on averaged results from multiple datasets.
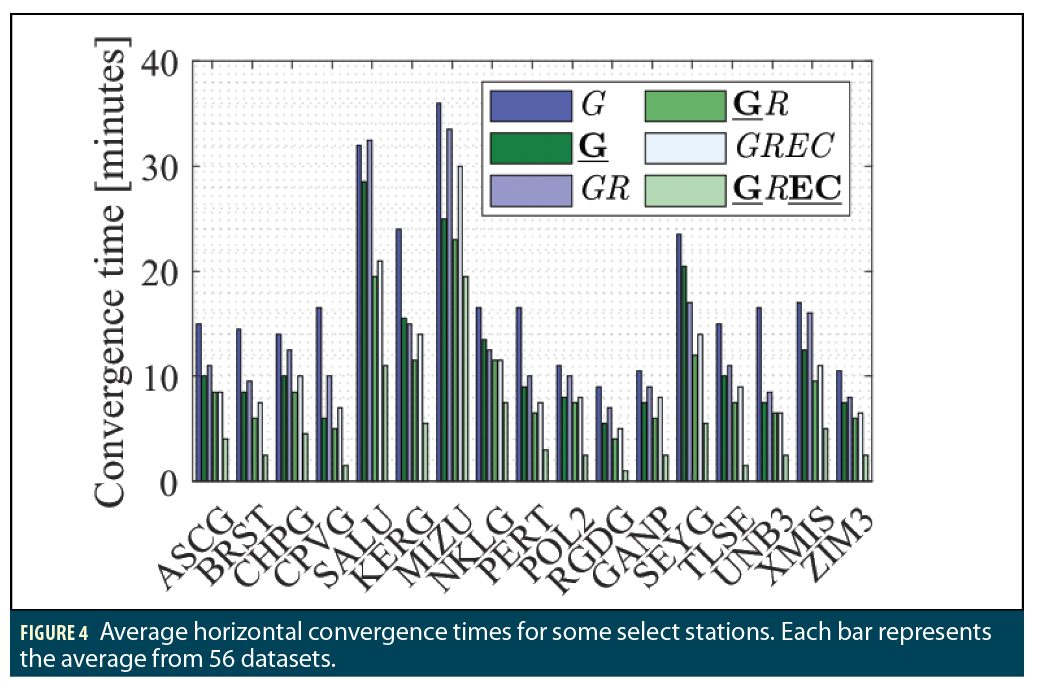
Figure 4 gives examples of the convergence time behavior of some select stations that were used for the generation of the Figure 3 results. For most datasets, a fixed GPS solution converges faster than a float GR solution, and a fixed GR solution converges faster than a float GREC solution. For some datasets, the fixed GPS solutions converge faster than the float GREC solution, but those datasets are exceptions. These results indicate that there can be more benefit to implementing AR on a few select constellations, as opposed to processing more satellites, or even expanding the constellations with more satellites. Naturally, a GREC fixed solution has a better behavior than all other solutions, as it adds robustness to the fixing and greatly reduces the convergence time for all datasets.
Looking at these results, it is obvious that Ambiguity Resolution is a very valuable tool, even with the increasing number of satellites and constellations that the GNSS world is currently witnessing. Performing ambiguity resolution on fewer constellations can lead, in many instances, to a better PPP performance in comparison to processing multiple constellations without any AR. However, that does not belittle the importance of multi-GNSS processing. The previous plots show that performing AR on as many constellations as available leads to improvements to the solutions, making four constellations AR the optimal processing mode. However, these results bring up the question of the importance of multi-GNSS processing in the current AR context: Can processing an ever- increasing number of satellites and constellations lead to ever-improving PPP performance? The following section attempts to answer this question through analyzing the performance with the presence of obstructions.
Multi-GNSS AR in Obstructed Environments
This section builds on the previous section’s conclusion that processing fewer satellites with AR can be more beneficial to the PPP solution than processing more satellites. It tries to assess the dependence of both the float and fixed solutions on the PDOP and the number of satellites through applying obstructions in the form of different elevation angle masks. On top of the unobstructed solution with a 10° elevation mask, three additional solutions are investigated: 20°, 30° and 40° elevation masks.
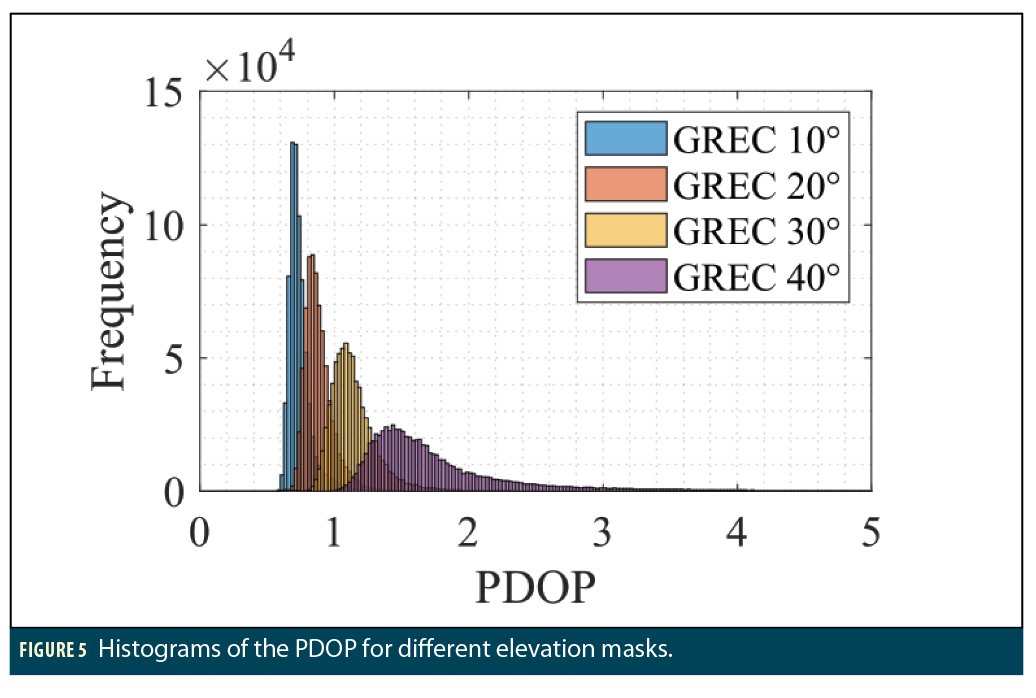
To show the effect of the obstructions on the PDOP, Figure 5 displays distribution of the PDOP for the GREC combination with different elevation masks. The bin size is 0.025 for the PDOP. As expected, as the obstructions are increased through an increase of the elevation angle threshold, the PDOP values become bigger. Note that the Gaussian curves become flatter (smaller peaks and bigger standard deviations) as the elevation angle threshold is increased. This change leads to a bigger variation in the behavior of different datasets as the PDOP takes larger ranges and values.
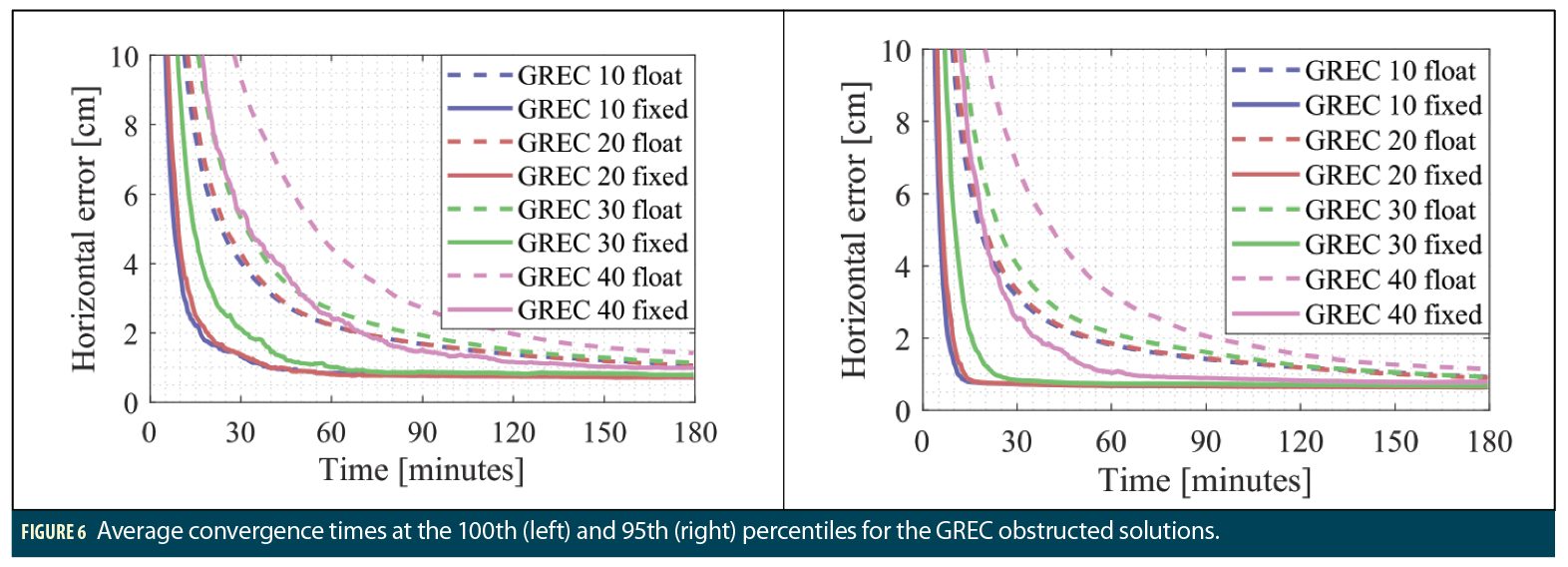
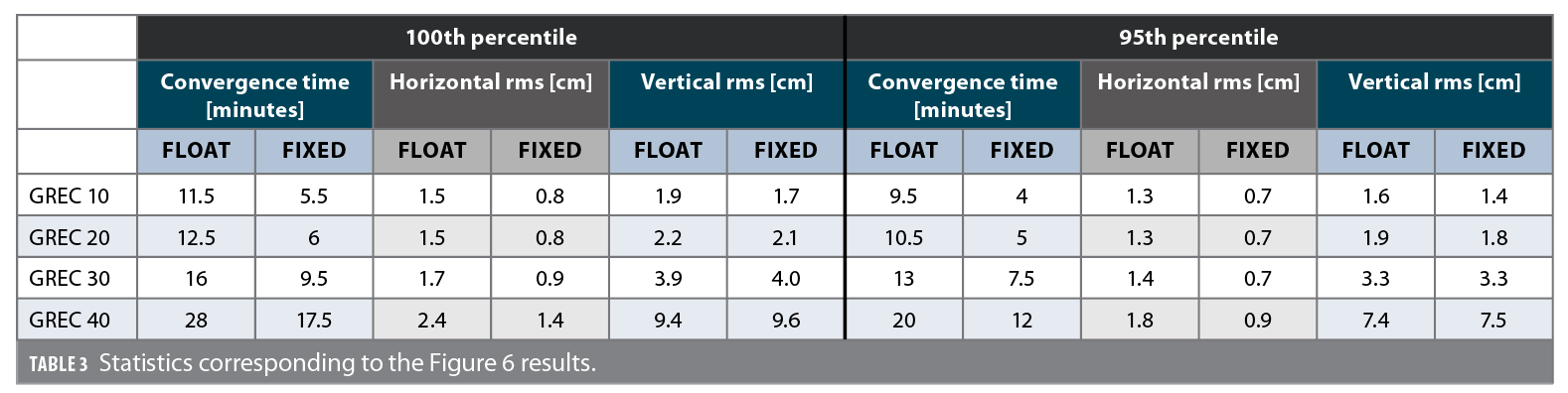
Figure 6 and Table 3 highlight the performance of the float and fixed, obstructed and unobstructed GREC solutions at the 100th and 95th percentiles. As stated earlier, GLONASS has been processed without ambiguity resolution in the fixed GREC solutions.
It is clear from all the results that creating more obstructions leads to both float and fixed solutions taking a longer time to converge. The horizontal accuracies are also affected, but to a lesser extent, as they remain within 1 cm of each other. The biggest difference in the horizontal rms is between the float unobstructed solution, 1.5 cm rms, and the float 40° obstructed solution, 2.4 cm rms—a 0.9 cm difference. The differences between the solutions are more noticeable when it comes to the convergence time and vertical accuracy. For the vertical component, AR doesn’t provide much improvement to the final accuracies, on which the obstructions have a consequent effect. Indeed, while the horizontal accuracies stay within 1 cm between the 10° and 40° elevation cut-offs, the vertical ones see variations of 8 cm, as they almost quintuple from 1.9/1.7 cm to 9.4/9.6 cm.
When it comes to the convergence time, while it is very close for the GREC 10 and GREC 20 solutions (both with and without AR), the effect of the obstructions becomes more evident with the 30° and 40° elevation masks. This result can be explained by looking at the Figure 5 PDOP histogram: GREC 10 and GREC 20 both have relatively close PDOP distributions with means of 0.7 and 0.9, respectively, while GREC 30 and GREC 40 have mean PDOP values of 1.2 and 1.9. The range of PDOP values also increases with elevation thresholds of 30° and 40°, which leads to bigger variations in the solutions.
On a brighter side, it is promising to see that even with at a 30° elevation angle threshold, the fixed solution is able to converge faster than the unobstructed solution, both at the 100th and 95th percentiles. When it comes to the GREC 40 solution, at the 100th percentile, even though there is a big improvement compared to its float counterpart, the solution’s convergence time is only comparable to the float GREC 30 solution. However, it is interesting to note that, at the 95th percentile, the GREC 40 fixed solution is much closer to the GREC 10, GREC 20 and GREC 30 float solutions, being only 2.5, 1.5 and 1 minute away, respectively. The fixed GREC 40 solution on the other hand converges at a time between the GREC 20 and GREC 30 float solutions.
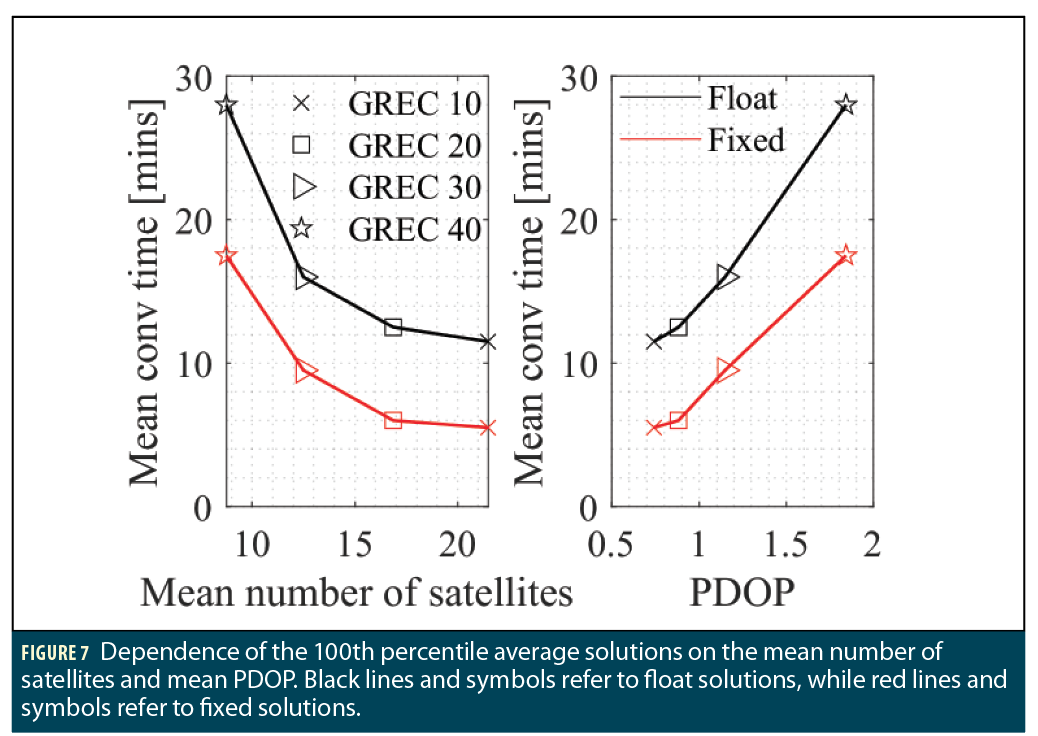
Figure 7 summarizes the dependence of the 100th percentile average solutions on the mean PDOP and the mean number of satellites through a correlation plot. Each mean value is based on the average results of all 2000 processed datasets.
The same conclusion holds that increasing the obstructions increases the PDOP and decreases the number of satellites, leading to longer convergence times. Both the float and fixed solutions follow similar trends, and the improvement that the fixing brings to the float solution seems to be relatively constant, regardless of the number of satellites/PDOP. On the other hand, it seems that the number of satellites has less effect on the convergence time as the former increases. Indeed, having a mean number of satellites of 12.5 instead of 8.7 (around 4 additional satellites) leads to a 43% to 46% decrease in the convergence time for both the float and fixed solutions. These additional 4 satellites lead to a decrease of 0.7 in the PDOP, from 1.8 to 1.2.
On the other hand, although there are almost 3 additional satellites between the GREC 10 and GREC 20 solutions, the PDOP is still similar, and so is the convergence time. Therefore, extrapolating the plot for a higher number of satellites, we can expect the curve to become more and more horizontal, as adding more satellites does not provide much new information or improvement to the satellite geometry, leading to a stagnation of the PPP performance. This plot is important in highlighting the benefits of PPP-AR, as it shows that processing an ever-increasing number of satellites might not be the answer to improving the PPP performance, but it is rather important to look at other techniques to improve it such as ambiguity resolution in which additional information is used in the form of the integer nature of the ambiguities. In that case, the graph gets shifted downwards and leads to improved PPP performance.
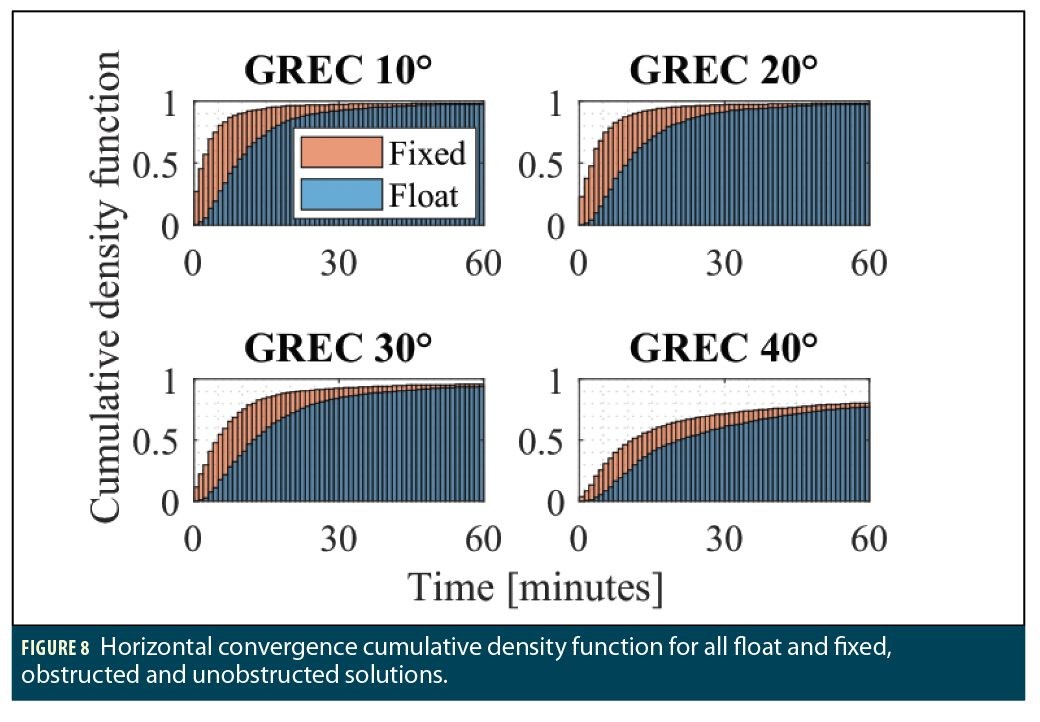
Finally, in order to provide an overview of the performance of the solutions at the dataset level, the cumulative density function of the convergence of all datasets for the eight solutions is shown in Figure 8. The plots show, at each epoch, the percentage of datasets that have converged by then—the convergence being defined as the time it takes for the horizontal error to settle below 10 cm.
Similarly to the previous analysis, the GREC 10 and GREC 20 solutions have similar behavior both in the float and fixed modes as 55% of the float GREC 10 solutions and 90% of the fixed GREC 10 solutions converge within the first 10 minutes, compared to 50% and 88% for the float and fixed GREC 20, respectively. On the other hand, 39% of the float GREC 30 solutions converge in the first 10 minutes, as opposed to 74% in the fixed case. Therefore, the effect of the obstructions becomes more noticeable with the 30° elevation mask although the fixed solutions are still able to perform relatively well.
Unfortunately, that is not the case with a 40° elevation mask, as only 24% of the float solutions and 47% of the fixed solutions converge in the first 10 minutes. Although the number of datasets that were able to converge in the first ten minutes for the fixed GREC 40 solution is comparable to the number of converged datasets for the float GREC 10 solution, that percentage is still relatively low compared to the GREC 10 unobstructed fixed case.
Conclusions
We have analyzed the importance of AR in the current multi-GNSS context, and the importance of multi-GNSS processing in the AR context. Performing AR on fewer constellations can lead in many instances to better PPP performances than float solutions with more constellations. For instance, GPS-AR has been proved to provide better convergence times and accuracies than float GPS + GLONASS solutions, and even, in some instances, than quad-constellation float solutions.
The quad-constellation fixed solution had the best performance out of all solutions. This proves that AR is still very relevant even in the current context with as many constellations and satellites available in orbit as ever.
The second point was analyzed through processing full quad-constellation solutions with different elevation angle masks, leading to different PDOP distributions, which affected both the float and fixed multi-GNSS solutions. An interesting relationship between the number of satellites and the convergence time was found: a decrease in the number of satellites leads to an exponential increase in the convergence time, or, if seen the other way, an increase in the number of satellites leads to an exponential decrease in the convergence time—law of diminishing returns. This exponential trend means that there is a stagnation in the impact of the number of satellites on the PPP performance with around 16 satellites and more on average.
On the other hand, the PPP-AR solution consistently performs better than the float solution regardless of the number of satellites. Therefore, while it is not possible to keep decreasing the PPP convergence time through the processing of more satellites because of the exponential relationship between the two, it is important to use alternative techniques such as AR to further improve the PPP performance. Future work will involve extending the analysis to triple-frequency data as GPS, Galileo and BeiDou can provide three frequencies or more. We expect that this would help the fixed solutions converge faster.
Acknowledgments
The authors would like to thank the IGS (International GNSS Service) for the global network of observation data, GFZ (GeoForschungsZentrum) for the rapid satellite orbits and clocks, CNES (Centre National d’Etudes Spatiales) for the satellite code and phase biases, and York University for research funding.
Authors
Nacer Naciri is a Ph.D. student at York University, Toronto, Canada in the Department of Earth and Space Science and Engineering. He received an engineering degree in aeronautics engineering from ISAE-SUPAERO in France, and an M.Sc. in aerospace engineering from KTH Royal Institute of Technology in Sweden.
Sunil Bisnath is a professor in the Department of Earth and Space Science and Engineering at York University. He received his Ph.D. in geodesy and geomatics engineering from the University of New Brunswick. For 25 years, he has been actively researching GNSS processing algorithms for positioning and navigation applications.






