A set-based urban positioning paradigm.
DANIEL NEAMATI, SRIRAMYA BHAMIDIPATI,
GRACE GAO, STANFORD UNIVERSITY
3D mapping aided GNSS localization provides state-of-the-art urban positioning by leveraging 3D building maps to account for reduced satellite visibility. Shadow matching is at the core of 3D mapping aided GNSS whereby the user matches the signal degradation at the receiver to the predictions from a 3D building map. Unfortunately, symmetries in building geometry yield multiple regions where the user could be located. With set-based techniques, we can fully account for these ambiguous regions and process the GNSS pseudorange information over each region individually to improve localization.
GNSS Shadows in Urban Environments
City dwellers and urban autonomous systems rely on the Global Navigation Satellite System (GNSS) to provide absolute location services. However, urban infrastructure often degrades standalone GNSS systems [1,2], thereby preventing reliable positioning, navigation and timing. Buildings block, diffract and reflect the line-of-sight (LOS) GNSS signals, thus inducing non-line-of-sight (NLOS) and multipath effects. 3D mapping-aided GNSS (3DMA GNSS) localization has gained traction over the past decade with the increasing availability of high-accuracy 3D city models. Shadow matching is a popular technique for 3DMA GNSS [3,4], among others, such as ray tracing [5,6] and machine learning-based GNSS [7]. Chiefly, the GNSS shadow refers to the areas where city infrastructure blocks direct LOS signals from a GNSS satellite. The user refines the location estimate by determining if the user is inside or outside the GNSS shadow, generally using signal features like signal-to-noise ratio. In this way, the user can turn NLOS and completely blocked signals into valuable information for localization. In past Inside GNSS articles, several authors elaborate on the critical role of shadow matching in 3DMA GNSS [8-11].
While shadow matching improves reliable urban positioning, particularly in the cross-street direction, it also suffers from challenges that restrict its performance. A discussion of the challenges in shadow matching is included in [12], with two two key challenges being a) along-street accuracy is often not reliable and b) multiple positions with large scores yield a multi-modal and ambiguous localization. With a denser urban scene, the location ambiguity often worsens.
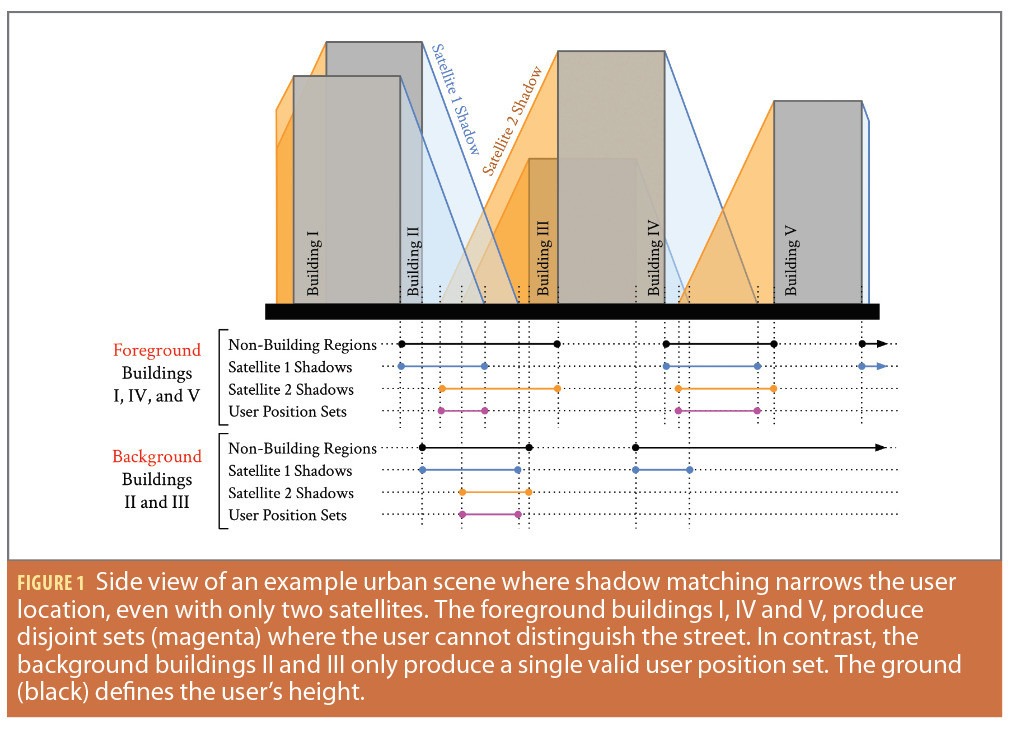
We illustrate these challenges in Figure 1, where we extend the common two-dimensional depiction of shadow matching to a slightly larger scene with two streets and different buildings in the foreground and background. The task of shadow matching is to narrow the user location based on the GNSS shadows. For clarity, we only show the shadows of two satellites. The satellite’s shadow is the color-coded region from the building roofs to the ground where the user would receive a highly degraded (i.e., NLOS) GNSS signal or no signal. If the user is on the street outside and has received an NLOS signal or no signal from both satellites, the magenta segments are the only valid user position sets. With only two moderate-elevation satellites, we significantly narrow the user’s location. However, we have not narrowed the along-street dimension (i.e., foreground and background) and we have multiple disjoint valid user sets, so the localization is ambiguous.
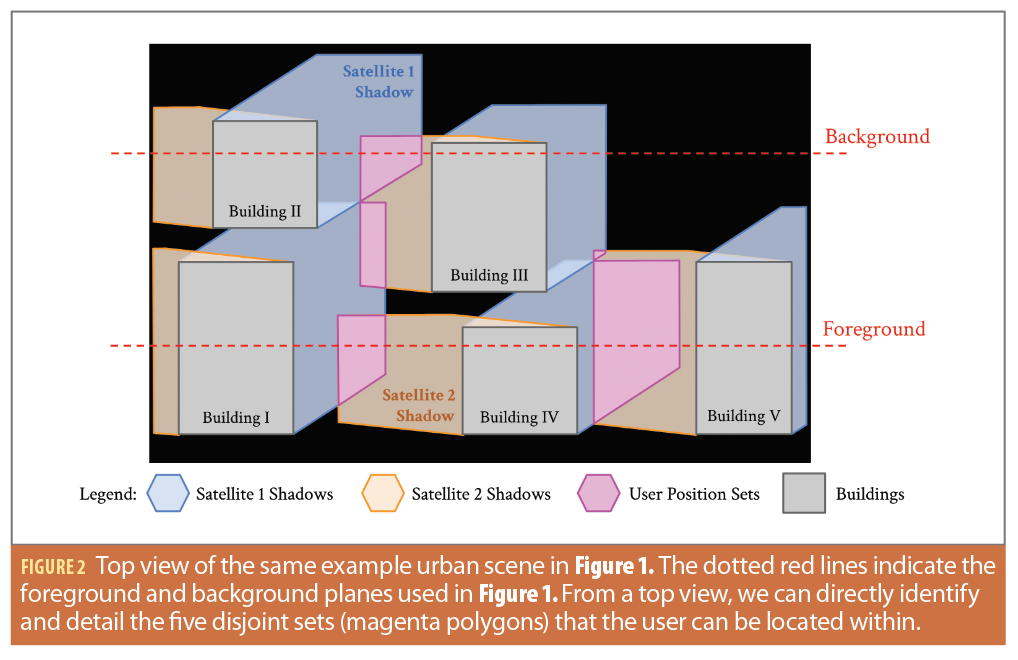
We further illustrate these issues of ambiguous localization in Figure 2 as a top view of the scene. The azimuth distribution of satellites is often helpful to localization, especially in cities where building height is variable and buildings have gaps between structures. In Figure 2, the satellites are roughly 140 degrees separated in azimuth. From the top view, we can fully detail the valid user set as a 2D polygon (magenta). In this example scene, there are five disjoint sets for the user position sets that match the user being on the street outside and having received an NLOS signal or no signal from both satellites. We could further reduce the valid user set into smaller sets with additional satellites. However, we are often left with multiple disjoint regions that match the available GNSS shadow information, especially in the along street direction [13].
One possible strategy for improving shadow matching’s along-street accuracy and reducing multi-modal ambiguities in localization is to fuse shadow matching with GNSS pseudoranges. Several authors pioneered this work in improving the urban position accuracy via weighted integration of shadow matching position solutions with that of likelihood-based 3D-mapping-aided GNSS pseudorange ranging [14-16]. The different integration options are reviewed and analyzed in [16]. These methods were further developed into a multi-epoch grid filtering framework in [17,18], which demonstrated improved along-street and cross-street accuracy.
These works built upon prior shadow matching filtering work, such as [19], that combined shadow matching in particle filter and Kalman filter frameworks to resolve multiple modalities over time.
The Set-Based Positioning Paradigm
While past 3DMA GNSS techniques have been successful, they rely on formulating shadow matching in a grid-based manner, which may not be as suitable as a set-valued approach for some users. As illustrated in Figures 1 and 2, shadow matching can be geometrically posed in the following set-based terms: the user is either in the shadow (which is a 2D set or polygon) or outside the shadow (which is the complement set). Set-based formulations conveniently circumvent the need for a grid of position candidates or discretization of elevation and azimuth angles, which is present throughout the aforementioned grid-based works.
Early works in set-based shadow matching [3, 20, 21] struggled to match the computational efficiency of grid-based shadow matching and handled the buildings on a surface-by-surface basis with raster-based techniques that were difficult to scale to dense scenes. In our prior work [13,22], we independently derived set-based shadow matching and designed a novel set-based technique known as Zonotope Shadow Matching (ZSM). Unlike [20, 21], ZSM formulates the entirety of shadow matching with set-based objects. That is, even the buildings are stored as three-dimensional sets. Using the mathematics of constrained zonotopes, we efficiently compute the shadows online using fast vector concatenation operations.
ZSM then iteratively performs set intersection and subtraction to refine a set-based Area of Interest (AOI), i.e., the extent of the depicted ground (black) in Figures 1 and 2. A more complete discussion of the mathematics is included in [13, 22, 23]. Importantly, ZSM may be the algorithm of choice for users who require changes in scales (e.g., from the large scale of a coarse estimate to the small scale of a refined estimate), both online and offline computational efficiency, set-based continuum localization for downstream processing, and complete shadows in a minimal memory representation. In this way, we endeavor to introduce a new set-based paradigm to shadow matching.
To incorporate the GNSS pseudorange information, we leverage the set-based framework from ZSM to form a set-based method to process the GNSS pseudoranges in our recent work [24]. We then develop an iterative set-based filter that exploits the set-based form of the GNSS pseudoranges.
First, we propose Satellite-Pseudorange Consistency (SPC) objects that use the satellite position and pseudorange measurement to transfer set-based information in the two-dimensional receiver position domain among the satellites. The multipath and NLOS effects are notoriously difficult to efficiently model in urban settings [5,6]. The set-based SPC representation allows an efficient, compact, conservative representation of the uncertainty bounds without performing computationally expensive ray tracing. In essence, we trade off the precision of ray-tracing techniques for a more tractable and conservative set-based approach. As discussed in prior works [12, 15, 16], GNSS pseudoranges are most informative in the along-street direction. Second, we fuse a recent history of pseudorange measurements via an iterative filter. Our strategy shares some conceptual similarities with the hypothesis-domain integration in [15, 16] in that we integrate the information at the hypotheses level. However, we diverge significantly from these works with (1) using set-based projections rather than scoring over a grid, (2) explicitly reducing the mode ambiguity, (3) exploiting the slow shadow change compared to the pseudorange variability, and (4) not requiring an NLOS error distribution (e.g., past works assume skewed normal innovation vectors [16]). Our new method directly addresses the challenges of along-street inaccuracy and multi-modal ambiguity reduction identified by [12]. But, our method also significantly relaxes the requirements on shadow matching initialization, model discretization, and uncertainty quantification, all of which [12] considers important advances to shadow matching robustness for reliable urban GNSS localization.

Set-Based GNSS Pseudorange Processing
Unlike other works in urban localization, we leverage the four-dimensional conic geometry of the pseudorange measurement model to handle the pseudorange measurements in a fully set-based framework. Explorations of the four-dimensional conic geometry are largely constrained to the analytical GPS literature [25-28]. We combine the clock bias, environment bias (e.g., multipath) and additional noise into a single term called the range offset. The satellite-dependent range offset is approximately shared across satellites when the receiver clock bias dominates the range offset, the signal is LOS, or when the biases are similarly positively correlated across satellites. The receiver state reflects both the receiver position and overall range offset.
In shadow matching, we implicitly assume the shadows are cast onto a ground plane, as in Figure 1. As noted in [14], terrain aiding significantly improves urban localization, especially when processing pseudoranges. In terrain-aiding, we constrain the receiver state with information on the terrain model and a rough estimate of the receiver height.
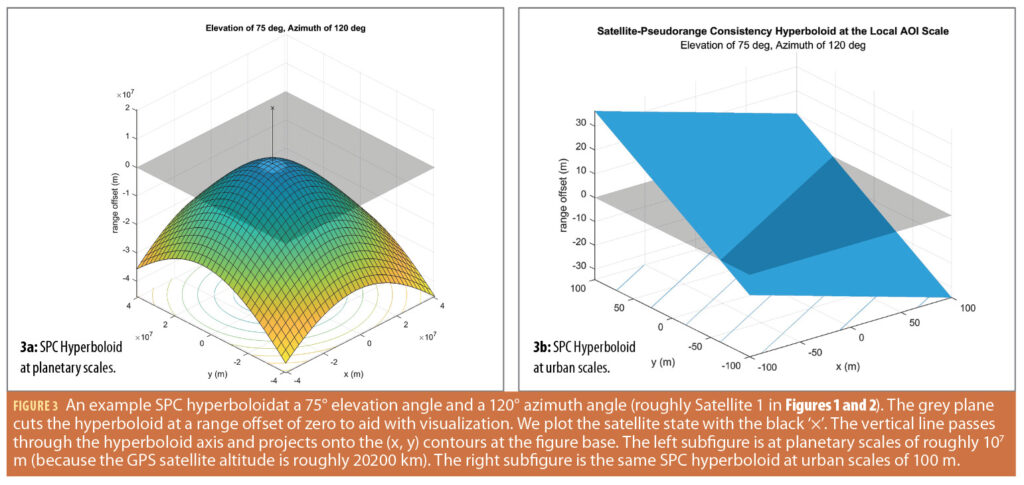
This terrain information restricts the user state, thereby yielding a hyperboloid in the three dimensions. This represents all the receiver states consistent with the satellite position, corrected pseudorange and terrain. We call this the Satellite-Pseudorange Consistency (SPC).
The satellite elevation describes the trade between the horizontal plane of the ground versus the vertical. So, the shape of the hyperboloid changes with the satellite elevation angle where the slopes of the hyperboloid near the peak are more shallow as the elevation increases. We provide an example SPC hyperboloid in Figure 3. The zero range offset plane in Figure 3a illustrates the circle in horizontal position space (x, y) consistent with no range offset between the true range and corrected pseudorange.
At the scales of city blocks, the surface is nearly perfectly planar, even for satellites at high elevation angles (Figure 3b). So, we can linearize the hyperboloid about the center of the AOI. We denote the linearization of the SPC hyperboloid as the SPC plane. More mathematical details are provided in [24].
Iterative Set-Based Filter
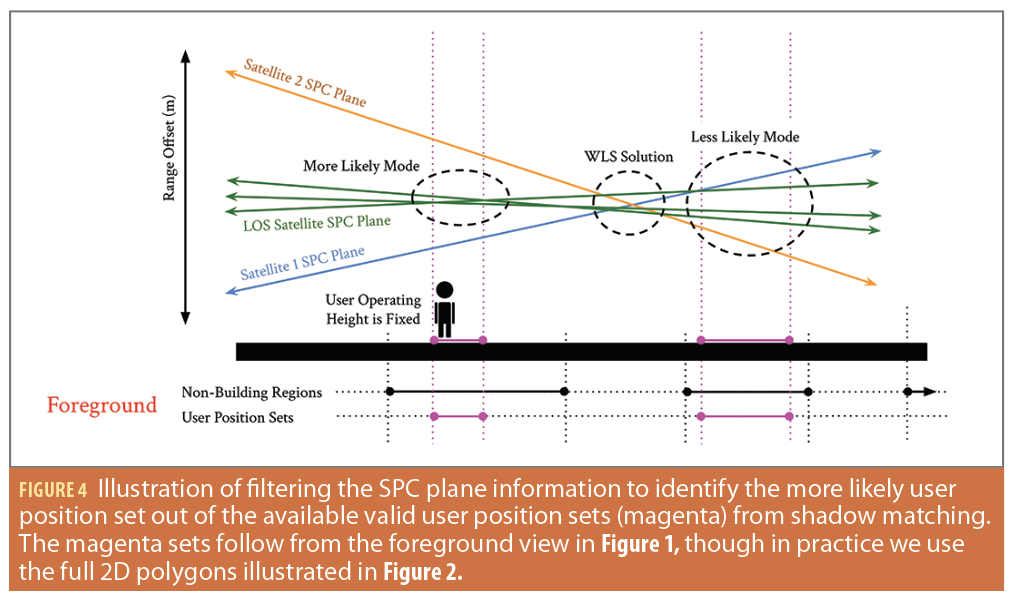
We design a filtering framework that iteratively combines the information from ZSM and the SPC planes. We summarize the core intuition of the filter in Figure 4. We start with a uniform prior belief over the disjoint sets (magenta in Figure 4, matching Figure 1). First, we construct the SPC planes for each GNSS signal while fixing the user operating height. In blue and orange, we include the SPC planes of satellites 1 and 2 in the foreground of Figure 1. We include the SPC planes of three additional LOS satellites (green) for filter illustration purposes. A base WLS solution with terrain-aiding would find the point with minimum distance to the SPC planes, which can be far from the user position in urban settings. In contrast, we leverage the disjoint sets from ZSM to reduce the locations that the user can be. We form a mixture model to fuse information across satellites in the range offset domain. We weigh the satellites with the probability that the satellite is a LOS satellite. We then find the disjoint set where the fused information is most consistent to determine the more likely option of the disjoint sets from ZSM. When a few LOS satellites are present, this is largely where the LOS satellite SPC planes are nearest each other. In Figure 4, the left magenta set is more likely than the right magenta set because the LOS satellite SPC planes are closer and more overlapping in the range offset domain. From there, we iterate over multiple timesteps to better identify that the left set is the correct set for the user location. More mathematical details are provided in [24].
Performance with Real-World Data
We test the impact of both parts of our approach from [24]: (1) the LOS-weighted set-based SPC projections and (2) the iterative set-based filter. We assess the first part by comparing the SPC projections to shadow matching alone (i.e., ZSM). We further assess the first part by comparing the LOS-weighting in the mixture model to the unweighted mixture model. We test the second part of the approach by comparing a single-step filter to the iterative filter. We validate the filter performance with both a small and a large AOI.
1. Experiment platform and LOS classifier
We collected static-user data with the GNSS Logger App at 1 Hz on a Pixel 3 phone in the Financial District of San Francisco. The user is at the curb on Fremont Street north of Mission Street and outside the Salesforce West building.
The user environment is a significant urban canyon with three prominent glass-facade buildings and two prominent buildings with mixed concrete-glass facades, as illustrated in Figure 5. For ease of processing the signals from the GNSS Logger App, we only use GPS L1 signals though the method herein discussed can be extended to multi-constellation and multi-frequency in future works. We use the same 150 s timeseries throughout the analyses.
We trained a probabilistic LOS Classifier in MATLAB using the TU Chemnitz smartLoc dataset [29]. We trained on the Frankfurt Main Tower, Frankfurt West End Tower and Berlin Potsdamer Platz sections. We tested on the Berlin Gendarmenmarkt section. We use logistic regression and only input the C/N0 data in the classifier. The final classifier has a 0.5-probability decision boundary at 34.5 dB-Hz between NLOS (negative class) and LOS (positive class). On the test set, we achieve a true positive rate of 69.8% and a true negative rate of 88.3%. Although the smartLoc dataset uses a ublox receiver, the logistic regression classifier generalizes well to the Pixel 3 phone. Further fine-tuning to adapt to the Pixel 3 phone would strictly improve classification but is outside the scope of this article.
2. Set-based shadow matching results
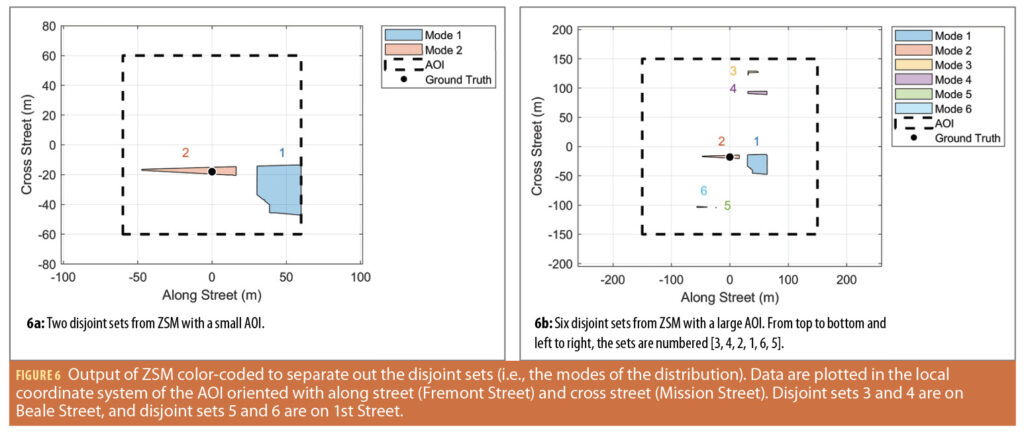
We use the ZSM algorithm detailed in [13, 22] to perform set-based shadow matching. Figure 6 illustrates the results of ZSM for a small AOI (120 m × 120 m in along and cross street directions) and a large AOI (300 m × 300 m in along and cross street directions). We observe two disjoint sets (i.e., a bimodal distribution) in the small AOI case with mode 2 (orange) as the correct mode. We incur six disjoint sets (i.e., six modes in the distribution) when we expand to a large AOI. Standard weighted least squares (WLS) incorrectly predicts mode 1 is the correct mode based on proximity throughout most of the experiment. For the large AOI, WLS incorrectly predicts modes 3, 4 and 5 at select time instances.
3. Set-based location ambiguity reduction
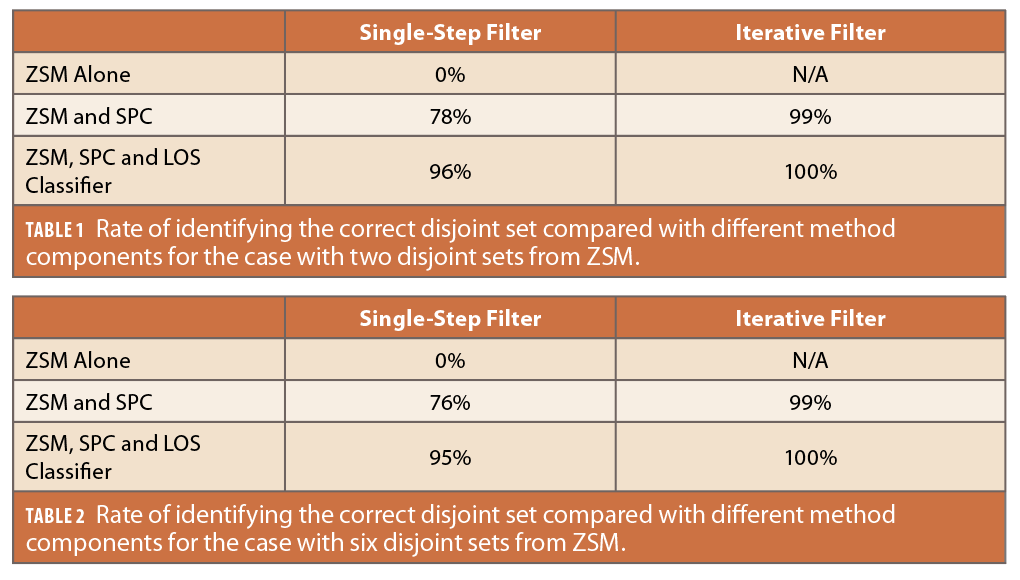
We first analyze how well the method components reduce the localization ambiguity for the case with two disjoint sets (Table 1).
The top performing combination is the proposed method (bottom right corner of Table 1) that starts with ZSM, uses the SPC projections, weights the measurements with the LOS classifier, and iteratively processes the pseudoranges over time.
We correctly arrive at the set with the user’s location in all timesteps with our proposed method for this data set. We also demonstrate how the iterative filter, SPC projections and LOS classifier work together to achieve the sought performance. First, the pseudorange information embedded in the SPC projections is critical in selecting the correct disjoint set. We identify the correct disjoint set in 78% of timesteps (from 0% in the uniform prior with ZSM alone) simply by including the SPC projections, even with a single-step filter. We improve to 96% when querying the LOS classifier to weigh the measurements. If we use an iterative design instead of the LOS classifier, we improve to 99%. Both these options improve the filter by rejecting the spurious NLOS and multipath-ridden outliers either by classification in the former case or by the temporal dispersion of the error in the latter case. We can reap the benefits of both options when we combine them in our proposed method because they work via different mechanisms. With the computational efficiency of the set-based method, the filter calculates the filter updates at roughly 3.7 ms per timestep and is fast enough for real-time operations.
The second case with six disjoint sets is more difficult for the filter as it must reject five incorrect sets in the face of conservative approximations in the SPC projections. Still, we see the filter identifies the correct set in all timesteps for this dataset (Table 2). Indeed, we arrive at similar results to the case with two disjoint sets. As before, the SPC projections are the most significant improvement as we move from an inability to identify the correct set in ZSM alone to identifying the correct set in 76% of the timesteps with the GNSS pseudorange. However, to achieve the sought performance of 100%, we require input from the LOS classifier and the iterative filter design.
The time to evaluate 150 timesteps only increases by roughly 200-300 ms (equivalently, 1-2 ms more per timestep) over the case with two disjoint sets. The method easily scales to larger AOIs with more multi-modal distributions.
Conclusion
We presented a new set-based paradigm for urban positioning. Our method reformulates past 3D mapping-aided techniques with computationally efficient set-based operations. In set-based shadow matching, we can fully represent the GNSS shadows without any discretization to better capture the shadow geometry. However, we retain similar issues of ambiguous locations where shadow matching produces multiple disjoint sets where the user could be located. To remedy this, we presented a fully set-based method to reduce location ambiguities in set-based shadow matching. Our proposed method had two key components: (1) processing GNSS shadows in a way conducive to set-based operations; and (2) iteratively filtering the pseudorange information via set-based operations to identify the most likely disjoint set from shadow matching. We validated our approach on smartphone data collected in the dense urban Financial District of San Francisco. We demonstrated both parts of the ambiguity reduction approach are critical to identifying the disjoint set that correctly matched the user location.
Our method is highly computationally efficient, and we can run the filter in roughly 3.7-5.4 ms per timestep depending on the number of disjoint sets. Given the 1 Hz data collection frequency in smartphones, this computational load is suitable for real-time operations. Our ongoing work includes leveraging higher-fidelity maps, quantifying the impact of classification or map uncertainty on the user’s positioning solution, and studying our set-based urban positioning paradigm in more diverse urban settings.
Acknowledgements
This material is based upon work supported by the National Science Foundation under Grant No. DGE-1656518. We would like to thank Shubh Gupta for reviewing portions of this article. Lastly, we would like to thank the Google Android Location team for free and open-source data processing tools for smartphone GNSS data.
References
(1) Hsu, L.-T. (2017). Analysis and modeling GPS NLOS effect in highly urbanized area. GPS Solutions, 22(1):7.
(2) Zhu, N., Marais, J., Betaille, D., and Berbineau, M. (2018). GNSS position integrity in urban environments: A review of literature. IEEE Transactions on Intelligent Transportation Systems, 19(9):2762–2778.
(3) Groves, P. D. (2011). Shadow Matching: A new gnss positioning technique for urban canyons. NAVIGATION, 64(3):417–430. Groves, P. D. and Adjrad, M. (2019). Performance assessment of 3D-mapping–aided GNSS part 1: Algorithms, user equipment, and review. NAVIGATION, 66(2):341–362.
(4) Wang, L., Groves, P. D., and Ziebart, M. K. (2015). Smartphone shadow matching for better cross-street gnss positioning in urban environments. NAVIGATION, 68(3):411–433.
(5) Miura, S., Hsu, L.-T., Chen, F., and Kamijo, S. (2015). GPS error correction with pseudorange evaluation using three-dimensional maps. IEEE Transactions on Intelligent Transportation Systems, 16(6):3104–3115.
(6) Suzuki, T. (2016). Integration of GNSS positioning and 3D map using particle filter. In Proceedings of the 29th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2016), pages 1296–1304.
(7) Van Diggelen, F. and Wang, J. (2020). Improving urban gps accuracy for your app.
(8) Wang, L., Groves, P., and Ziebart, M. (2013). Urban Positioning on a Smartphone. Inside GNSS, page 44–56.
(9) Irish, A., Iland, D., and Madhow, U. (2015). Urban Localization and 3D Mapping Using GNSS Shadows. Inside GNSS, page 60–66.
(10) Groves, P. (2016). It’s Time for 3D Mapping–Aided GNSS. Inside GNSS – Global Navigation Satellite Systems Engineering, Policy, and Design, page 50–56.
(11) Groves, P., Zhong, Q., Faragher, R., and Esteves, P. (2021). Supercorrelation Plus 3D Mapping-Aided GNSS. Inside GNSS.
(12) Groves, P. D., Wang, L., Adjrad, M., and Ellul, C. (2015). GNSS Shadow Matching: The Challenges Ahead. In Proceedings of the 28th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2015), pages 2421–2443.
(13) Bhamidipati, S., Kousik, S., and Gao, G. (2022). Set-valued shadow matching using zonotopes for 3d-map-aided GNSS localization. NAVIGATION: Journal of the Institute of Navigation, 69(4).
(14) Adjrad, M. and Groves, P. D. (2017). Enhancing Least Squares GNSS Positioning with 3D Mapping without Accurate Prior Knowledge. NAVIGATION, 64(1):75–91.
(15) Adjrad, M. and Groves, P. D. (2018). Intelligent Urban Positioning: Integration of Shadow Matching with 3D-Mapping-Aided GNSS Ranging. NAVIGATION, 71(1):1–20.
(16) Adjrad, M., Groves, P. D., Quick, J. C., and Ellul, C. (2019). Performance assessment of 3D-mapping-aided GNSS part 2: Environment and Mapping. NAVIGATION, 66(2):363–383.
(17) Zhong, Q. and Groves, P. D. (2021). Multi-Epoch 3D-Mapping-Aided Positioning using Bayesian Filtering Techniques. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), pages 195–225.
(18) Zhong, Q. and Groves, P. D. (2022). Multi-Epoch 3D-Mapping-Aided Positioning using Bayesian Filtering Techniques. NAVIGATION, 69(2).
(19) Wang, L. (2014). Kinematic GNSS shadow matching using a particle filter. In Proceedings of the 27th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2014), pages 1907–1919.
(20) Yozevitch, R., Ben Moshe, B., and Levy, H. (2012). Breaking the 1 meter accuracy bound in commercial GNSS devices. In 2012 IEEE 27th Convention of Electrical and Electronics Engineers in Israel, pages 1–5.
(21) Yozevitch, R. and Ben Moshe, B. (2015). A Robust Shadow Matching Algorithm for GNSS Positioning. NAVIGATION, 62(2):95–109.
(22) Bhamidipati, S., Kousik, S., and Gao, G. (2021). Set-Valued Shadow Matching using Zonotopes. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), pages 2373–2390.
(23) Scott, J. K., Raimondo, D. M., Marseglia, G. R., and Braatz, R. D. (2016). Constrained zonotopes: A new tool for set-based estimation and fault detection. Automatica, 69:126–136.
(24) Neamati, D., Bhamidipati, S., and Gao, G. (2022). Set-based ambiguity reduction in shadow matching with iterative GNSS pseudoranges. In Proceedings of the 35th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2022), pages 1093 – 1107.
(25) Bancroft, S. (1985). An Algebraic Solution of the GPS Equations. IEEE Transactions on Aerospace and Electronic Systems, AES-21(1):56–59.
(26) Abel, J. and Chaffee, J. (1991). Existence and uniqueness of GPS solutions. IEEE Transactions on Aerospace and Electronic Systems, 27(6):952–956.
(27) Chaffee, J. and Abel, J. (1994). On the exact solutions of pseudorange equations. IEEE Transactions on Aerospace and Electronic Systems, 30(4):1021–1030.
(28) Grafarend, E. W. and Shan, J. (2002). GPS Solutions: Closed Forms, Critical and Special Configurations of P4P. GPS Solutions, 5(3):29–41.
(29) Reisdorf, P., Pfeifer, T., Breßler, J., Bauer, S., Weissig, P., Lange, S., Wanielik, G., and Protzel, P. (2016). The problem of comparable GNSS results – an approach for a uniform dataset with low-cost and reference data. In Ullmann, M. and El-Khatib, K., editors, The Fifth International Conference on Advances in Vehicular Systems, Technologies and Applications, volume 5, page 8. ISSN: 2327-2058.
Authors
Daniel Neamati is a Ph.D. student in the Department of Aeronautics and Astronautics at Stanford University. He received his bachelor’s degree in Mechanical Engineering, with a minor in Planetary Science, from the California Institute of Technology. His research interests include urban GNSS, geospatial information, autonomous decision-making and risk-aware localization.
Sriramya Bhamidipati is a robotics technologist at the Jet Propulsion Laboratory (JPL). Prior to JPL, she was a postdoctoral scholar in Aeronautics and Astronautics at Stanford University. She received her Ph.D. in Aerospace Engineering at the University of Illinois, Urbana-Champaign in 2021, where she also received her M.S. in 2017. She obtained her B.Tech. in Aerospace from the Indian Institute of Technology, Bombay, in 2015. Her research interests include space robotics, GPS, artificial intelligence and unmanned aerial systems.
Grace Gao is an assistant professor in the Department of Aeronautics and Astronautics at Stanford University. Before joining Stanford University, she was an assistant professor at the University of Illinois at Urbana-Champaign. She obtained her Ph.D. at Stanford University. Her research is on robust and secure positioning, navigation, and timing with applications to manned and unmanned aerial vehicles, autonomous driving cars, as well as space robotics.




