It has been widely demonstrated that GNSS-based localization technologies are vulnerable to signal jamming and spoofing/replay attacks, where a receiver can be either denied positioning or deceived to compute a forged PVT solution. Today, it is possible to spoof a GNSS receiver to any arbitrary location and time in the world with many incidents being reported in the wild.
AANJHAN RANGANATHAN, ADAM BELFKI, PAU CLOSAS NORTHEASTERN UNIVERSITY
A recent work explored the impact of GNSS spoofing on unmanned aerial vehicles (UAVs). UAVs rely on multiple sensor modalities for critical navigation decisions. The study conducted experimental analysis to assess the feasibility and requirements of exerting complete control over a UAV’s movements solely by spoofing GNSS signals. The research described the challenges associated with achieving a comprehensive takeover of a UAV through GNSS spoofing, emphasizing the necessity of intricate manipulations of spoofing signals in real-time to ensure controlled flight without collisions. In other words, while off-the-shelf UAVs remain susceptible to GNSS spoofing attacks, achieving complete control over a single UAV requires real-time manipulation of spoofing signals, necessitating a sensing/actuation loop.
This work looked at the GNSS interference problem in the context of a single UAV. Today, there is growing interest in the use of autonomous swarms of robots in safety- and security-critical applications such as search and rescue missions, emergency support, construction efforts and delivery. Swarms also have significant applications in the military both from a tactical as well as logistic perspective. Precise positioning, navigation and communication systems are fundamental to the operations of these applications and it is unclear how spoofing and jamming attacks on localization systems impact the overall swarm ecosystem. For instance, a spoofing attack on a swarm of unmanned aerial vehicles can potentially lead to swarm collision and collapse or simply displacing its course.
In this article, we take the first step to investigate the vulnerabilities and resilience of swarms to spoofing attacks. Given the increasing adoption of distributed and decentralized algorithms due to their effectiveness against rapidly changing environments and elimination of a central control authority, this analysis focuses on a specific distributed and decentralized swarm architecture with the goal to uniformly distribute a drone swarm across a geographic region, ensuring each drone covers an equal area. This coverage task is essential in a wide variety of swarm missions including tracking, surveillance or simply navigating an area.
We analyze popularly deployed Voronoi tessellations with Lloyd relaxation aiming to understand the attack vectors that a coverage mission can encounter. We evaluate the behavior of swarms to GNSS spoofing attacks using a custom-built distributed swarm simulation framework that includes software like Gazebo, Ardupilot and QGroundControl. We present the key takeaways and offer suggestions for future research opportunities.
Swarm Scenario and Threat Assumptions
In this work, we focus on the impact of GNSS spoofing attack on swarm formation algorithms. We assume an adversary with the ability to generate and transmit GNSS signals. While the attacker’s specific objective could vary widely, ranging from forcing a drone to collide with other drones to creating a surveillance blackout area, we assert the primary goal of the spoofing attack is to force the swarm to behave differently than originally intended. We assume the UAVs fall within the radio range of the attacker and can, therefore, pick up these counterfeit signals. In other words, we assume the adversary has successfully spoofed the UAVs’ GNSS receiver, either through a seamless takeover technique or via a simple non-coherent overshadow attack. The susceptibility of standalone GNSS receivers to spoofing has been thoroughly explored in previous studies. We do not assume the availability of advanced spoofing mitigation countermeasures in these drones, as the cost would significantly impact the swarm’s deployment and operational scalability. We do not consider adversaries capable of injecting forged positions directly over the communication links, as these links generally have cryptographic security measures in place. We do not consider jamming attacks because while they might disrupt communications, the main goal of the attack is to manipulate the swarm into behaving in a specific manner.
Swarm architectures can be categorized as: centralized, decentralized and hybrid. Centralized systems have a single controller that coordinates the swarm, making it efficient but the controller becomes a single point of failure. Decentralized architectures distribute the decision making, thereby enhancing robustness. Hybrid architectures employ a hierarchical system that allows for centralized decision-making and autonomous local actions.
In our scenario, we consider a group of drones tasked with surveilling a specific geographic region, each designated to cover an equal area. To achieve this uniform distribution, the system uses Voronoi tessellation in conjunction with Lloyd’s relaxation. Each drone determines its location using GNSS and broadcasts this position to its peers. Every drone receives the locations of its neighboring drones in real time and computes its Voronoi tessellation based on this localized information. After determining its Voronoi cell, each drone navigates to the centroid of its designated cell and subsequently broadcasts its updated location. Upon receiving these new positions, the drones recalibrate, recompute their tessellations, and adjust again. This iterative process continues until the variance in the area covered by each drone falls below a pre-defined threshold. Once this condition is met, indicating a balanced coverage, the system is considered to have reached a stable state.
Impact of GNSS Spoofing on Swarm Formation
In our analysis, we focus on the decentralized architecture and the critical spatial coverage problem, which is fundamental to nearly every swarm scenario. Take, for example, a swarm of drones tasked with monitoring a large public event—a classic spatial organization challenge. These drones must efficiently scan the area to identify potential security threats or emergencies. Essential to this task is ensuring agents can effectively distribute themselves and coordinate within their environment, making the formation problem paramount in successful drone operations. Although there are several algorithms addressing the spatial organization problem, we focus on Voronoi diagrams and Lloyd’s relaxation algorithm.
Voronoi Tessellation and Lloyd’s Algorithm
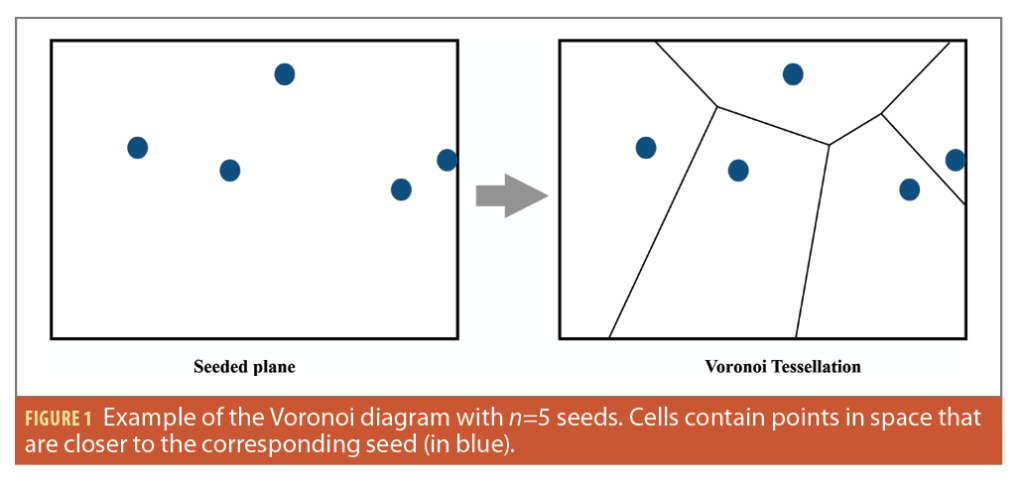
Voronoi tessellation, also known as Voronoi diagram, is a well-known mathematical concept in computational geometry used in various fields. It involves the partitioning of a plane with ‘n’ generated seeds into convex polygons called Voronoi cells with each polygon containing exactly one seed. This arrangement ensures for any given point in a given cell it is the closest to its seed than to any other. One might notice the similarities with coverage algorithms in unmanned vehicle swarms. Constructing the Voronoi diagram involves defining vertices and edges, delimiting each region. Vertices are points with three or more equally distant regions. The fundamental property of Voronoi cells is preserved by drawing edges perpendicularly to the midpoint between every pair of neighboring seeds (Figure 1). Several efficient algorithms have been proposed for constructing Voronoi diagrams leveraging the Delaunay triangulation.
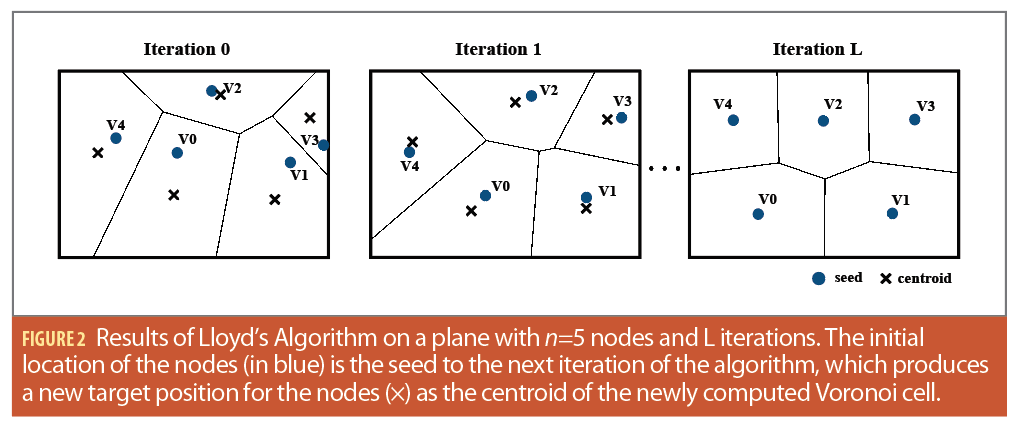
Lloyd’s algorithm, or Voronoi relaxation, is an iterative computational technique for redistributing points evenly in a region and partitioning subsets of Euclidean space into uniformly sized convex cells. After the Voronoi tessellation has been computed for the initial seed locations, Lloyd’s algorithm iteration propagates each seed to the centroid of its corresponding Voronoi cell resulting in more evenly distributed and uniformly shaped Voronoi cells.
This process minimizes variations in cell size and optimizes spacing between points. The algorithm continues iterating until the seed’s position is equal to the centroid, ensuring guaranteed convergence. To expedite convergence, a degree of tolerance can be introduced (Figure 2). The centroid of each Voronoi cell is calculated at every iteration using the vertices of the closed polygonal regions formed by the Voronoi diagram around each seed.
Spoofing Impact on Swarm Spatial Coverage
GNSS spoofing distorts the location perceived by drones. Also, it’s reasonable to assume such spoofing would impact only a subset of a drone swarm. This is largely due to the challenges of spoofing over a broad geographical region that a swarm might occupy. Targeted drones will then estimate and broadcast incorrect locations, leading to flawed positional data being incorporated into the Voronoi tessellation calculations of neighboring drones. The consequences of this are multifaceted. For one, the
algorithm may fail to converge, potentially causing drones to remain in motion for extended durations and depleting their batteries. Furthermore, this can create uneven surveillance patterns, with some drones covering areas too vast for them, leading to surveillance blind spots. If anti-collision measures are absent, drones might even collide. The algorithm’s dynamics become particularly intriguing when multiple drones, affected by spoofing, report identical locations. In such cases, the algorithm has to interpret this as two drones occupying the same spot, introducing additional complexities and potential system discrepancies.
In our analysis, we explore three distinct spoofing strategies to understand their impact on swarm behavior: i) “Fixed Spoofing,” where the false location remains constant throughout the spoofing duration, ii) “Relative Spoofing,” in which the deceitful location is set as a subtle deviation from the drone’s genuine location, and iii) “Random Spoofing,” where the misleading location is chosen arbitrarily.
By examining these strategies, we capture a broad spectrum of potential threats, providing valuable insights into the swarm formation algorithm’s resilience. Naturally, the depth of this study goes beyond these strategies, as several other parameters merit attention for their potential influence on the outcome, such as the choice of the drone targeted, the spoofed location, and the swarm’s physical configuration at the time of the attack. Another important variable is spoofing duration. We would like to highlight the distinction between continuous spoofing, where false signals are sent during the entire algorithm’s operation, and intermittent spoofing. Our initial hypothesis suggests continous spoofing might prevent the algorithm from converging, leaning more toward a denial-of-service attack. Moreover, constant spoofing signal transmission could reveal the attacker’s location, potentially making it an important choice for the adversary. Given these considerations, our analysis focuses largely on the effects of partial spoofing.
Experimental Analysis and Results
Simulation Testbed
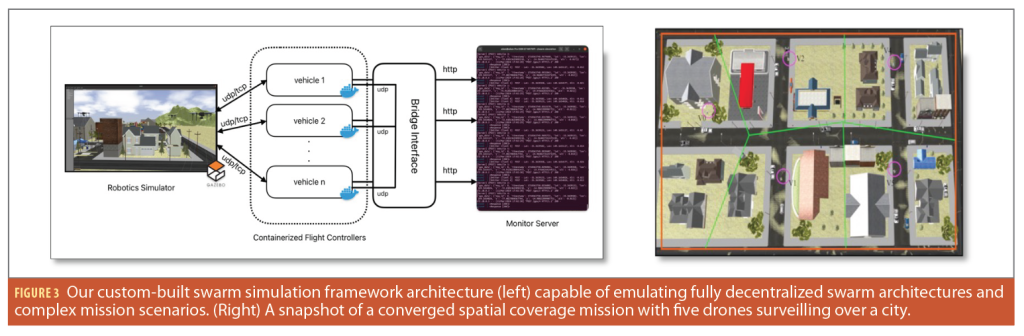
For our experimental analysis, we employ two distinct setups: a custom-built swarm simulation testbed (Figure 3) and a python-based algorithm simulator. Our custom-built swarm testbed can emulate a detailed model for each vehicle, linked to its own autopilot software. We use Docker to keep each vehicle’s software separate, essentially acting like its own computer within the swarm. These vehicles continuously transmit location and mission data to the Monitor server and are all connected through a bridge interface, which lets them communicate with each other and the main computer, truly simulating a distributed and decentralized environment. There’s also a special interface to set up and start simulations, allowing for complex mission planning. This setup includes a mission planner in the flight control systems that can handle detailed multi-layered mission instructions. This testbed allows testing against real-world scenarios and accounting for various environmental factors. The python-based algorithm simulator offers an interactive platform, focusing predominantly on the algorithm’s intricacies. This simulator enables systematic iteration of the algorithm and analysis of the swarm’s behavior, eschewing detailed environmental or drone modeling.
At each iteration, we can choose the spoofed vehicle and the spoofing location, i.e., absolute or relative. Additionally, the simulator can operate in a non-interactive mode, taking in parameters at the start, such as spoofing duration, vehicle ID and spoofing location. A practical simulator feature is its ability to provide visual feedback on how spoofing affects the swarm’s behavior.
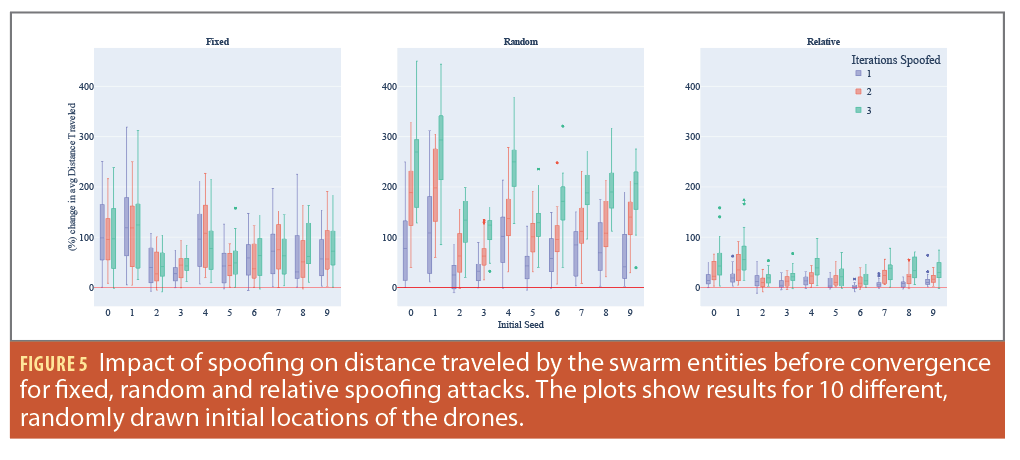
Evaluation Metrics and Results
In our study, we primarily focused on two evaluation metrics: i) the percentage change in the number of iterations required for the algorithm to converge, and ii) the percentage change in the total distance traveled by the drones. For our experiments, we varied the starting positions of the swarm’s drones, referred to as initial seed locations, and applied each of the three spoofing techniques: fixed, relative and random location manipulation. Furthermore, we investigated the consequences of manipulating the location for 1, 2, and 3 iterations of the algorithm’s execution time, considering each initial seed location and spoofing method. It’s noteworthy that each simulation was executed 75 times for every initial seed location. During each run, the drone being spoofed and the exact spoofed location were varied in accordance with the chosen spoofing technique.
Impact on Algorithm Convergence Time
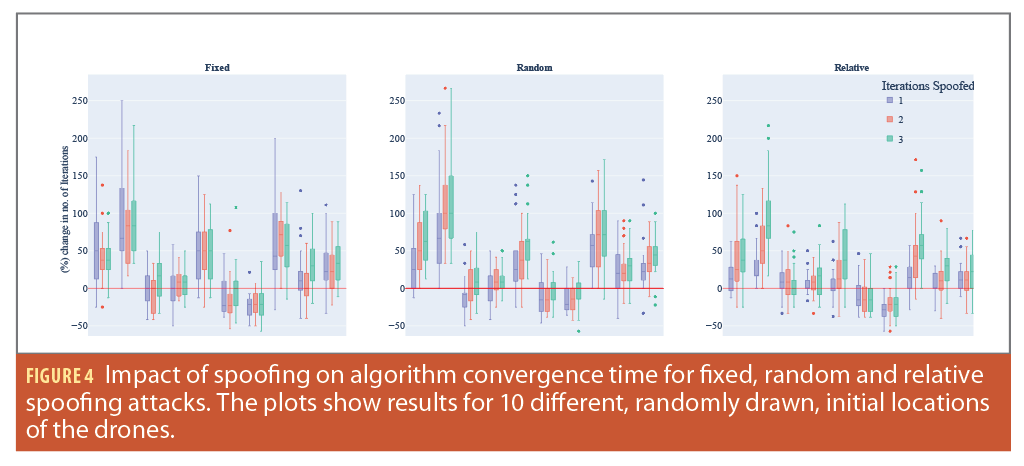
Our analysis results regarding the effects of location manipulation within the Voronoi/Lloyd’s relaxation algorithm for swarm formation is shown in Figure 5. It’s evident that manipulating drone locations does influence the algorithm’s convergence time for all the initial seed locations analyzed. A key highlight from these results is that for certain initial location seeds, spoofing can unexpectedly expedite the algorithm’s convergence. This phenomenon can be attributed to the fact some inherent swarm configurations naturally lead to a prolonged convergence and location manipulation and, in these instances, might inadvertently streamline the process. However, notice this faster convergence might not yield to a desirable formation, and instead one the attacker designed. This presents a potential strategy for adversaries, recognizing and consistently spoofing locations of specific drones in such configurations. It is worth noting that for certain seed locations, the algorithm’s convergence time increased by more than 200%, even with location spoofing limited to a single iteration.
Impact on Travel Distance
In a subsequent analysis, we shifted our focus to evaluate the impact of spoofing location on the distance traveled by the swarm entities. The results, illustrated as a box plot, represent the percentage change in the cumulative distance covered by the entire swarm. It’s observable from the data that spoofing typically results in an extended travel distance compared to the baseline distance in the absence of spoofing.
Notably, certain swarm configurations, when subjected to spoofing, led to a near 400% increase in the distance traveled by the swarm entities, amounting to roughly five times the typical distance. When considering relative spoofing, the impact is more restrained, with the distance traveled not exceeding twice the usual amount. This outcome aligns with expectations, given that relative spoofing introduces only a marginal location offset, as opposed to a more drastic location change.
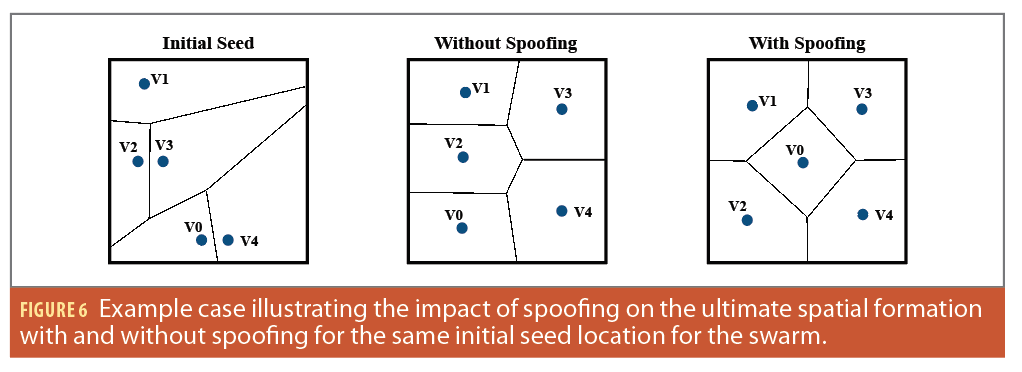
Impact on Final Spatial Organization
In our experimental analysis, we observed the final spatial configuration upon convergence could differ based on location manipulations for specific durations during the algorithm’s execution. As illustrated in Figure 6, the ultimate regions designated to each drone vary, depending on the presence or absence of spoofing. This observation suggests the potential for an attacker to craft and time spoofing signals, aiming to influence the swarm’s spatial orientation post-convergence. For instance, it’s conceivable that a compromised drone might be manipulated to monitor a particular area, thereby inducing a surveillance blind spot. Similarly, an adversary could aim to allocate a vast region to a drone, placing its centroid at a distance from the drone’s surveillance scope, which would result in a coverage gap. Such findings indicate an avenue for further research, exploring the prospect of achieving specific outcomes by merely spoofing the GNSS signals within a swarm.
Conclusion
In our study, we were guided by previous research highlighting the challenges of GNSS spoofing and the nuances of controlling individual UAVs. However, the broader impact of GNSS spoofing on drone swarms remained less explored. Our work sought to understand this area, particularly focusing on the swarm formation algorithms, as formation is an essential precursor to many swarm tasks.
Using our custom-designed simulation frameworks, we examined the effects of GNSS spoofing. Some significant findings include: spoofing led to nearly a 3× increase in convergence time, caused more than a 5× surge in the cumulative distance traveled by the drones, and notably influenced the swarm’s final spatial formation. Moving forward, we need to further explore the practical considerations for adversaries aiming to exploit GNSS spoofing. Additionally, a thorough evaluation of various swarm algorithms against potential adversarial tactics is warranted to develop more robust solutions.
Acknowledgements
This work has been partially supported by the NSF under Awards CISE-2144914, ECCS-1845833, and CCF-2326559. Research was also partially sponsored by the Army Research Laboratory and was accomplished under Cooperative Agreement Number W911NF-22-2-0001. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein.
This article is based on material presented in a technical paper at ION GNSS+ 2023, available at ion.org/publications/order-publications.cfm.
References
(1) Ioannides, R. T., Pany, T., and Gibbons, G. (2016). Known vulnerabilities of global navigation satellite systems, status, and potential mitigation techniques. Proceedings of the IEEE, 104(6):1174–1194.
(2) Amin, M. G., Closas, P., Broumandan, A., and Volakis, J. L. (2016). Vulnerabilities, threats, and authentication in satellite-based navigation systems [scanning the issue]. Proceedings of the IEEE, 104(6):1169–1173.
(3) Borio, D., Dovis, F., Kuusniemi, H., and Presti, L. L. (2016). Impact and Detection of GNSS Jammers on Consumer Grade Satellite Navigation Receivers. Proceedings of the IEEE, 104(6):1233–1245.
(4) Psiaki, M. and Humphreys, T. (2016). GNSS Spoofing and Detection. Proceedings of the IEEE, 104(6):1258–1270.
(5) MIT Tech Review (2019). Ghost Ships, Crop Circles, and Soft Gold: A GPS Mystery in Shanghai.
(6) Sathaye, H., Strohmeier, M., Lenders, V., and Ranganathan, A. (2022b). An experimental study of GPS spoofing and takeover attacks on UAVs. In 31st USENIX Security Symposium (USENIX Security 22), pages 3503–3520.
(7) Kling, M. T., Lau, D., Witham, K. L., Closas, P., and LaMountain, G. M. (2022). System for Closed-Loop GNSS Simulation. US Patent App. 17/662,822.
(8) Abdelkader, M., Guler, S., Jaleel, H., and Shamma, J. S. (2021). Aerial swarms: Recent applications and challenges. Current robotics reports, 2:309–320.
(9) Ranganathan, A., Belfki, A., and Closas, P. (2023). Analyzing the Impact of GNSS Spoofing on the Formation of Unmanned Vehicles Swarms. In Proceedings of the 36th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2023), pp. 3138-3147.
(10) Du, Q., Faber, V., and Gunzburger, M. (1999). Centroidal Voronoi tessellations: Applications and algorithms. SIAM review, 41(4):637–676.
(11) Lloyd, S. (1982). Least squares quantization in PCM. IEEE transactions on information theory, 28(2):129–137.
(12) Tippenhauer, N. O., Popper, C., Rasmussen, K. B., and Capkun, S. (2011). On the requirements for successful GPS spoofing attacks. In Proceedings of the 18th ACM conference on Computer and communications security.
(13) Ranganathan, A., Olafsdottir, H., and Capkun, S. (2016). SPREE: A spoofing resistant GPS receiver. In Proceedings of the 22nd Annual International Conference on Mobile Computing and Networking.
(14) Nighswander, T., Ledvina, B., Diamond, J., Brumley, R., and Brumley, D. (2012). GPS software attacks. In Proceedings of the 2012 ACM Conference on Computer and Communications Security.
(15) Sathaye, H., LaMountain, G., Closas, P., and Ranganathan, A. (2022a). Semperfi: Anti-spoofing GPS receiver for UAVs. In Network and Distributed Systems Security (NDSS) Symposium 2022.
(16) Brambilla, M., Ferrante, E., Birattari, M., and Dorigo, M. (2013). Swarm robotics: a review from the swarm engineering perspective. Swarm Intelligence, 7:1–41.
Authors
Aanjhan Ranganathan is Assistant Professor at Northeastern University, Boston. His research revolves around the security and privacy of wireless networks with a strong focus on autonomous cyber-physical systems and smart ecosystems. He is a recipient of several awards, including the prestigious NSF CAREER award, the outstanding dissertation award from ETH Zurich, the regional winner of European Space Agency’s Satellite Navigation competition, and the Cyber Award from armasuisse (Switzerland’s Department of Defense).
Adam Belfki is a fifth-year undergraduate student at Northeastern University Khoury College of Computer Sciences. He is majoring in computer science with a minor in math and a concentration in artificial intelligence. His research focuses on distributed and decentralized systems with applications in distributed coverage of swarms and blockchain consensus protocols.
Pau Closas is Associate Professor at Northeastern University, Boston. He received MS and Ph.D. degrees in Electrical Engineering from UPC in 2003 and 2009. He also holds a MS in Advanced Mathematics from UPC, 2014. His primary areas of interest include statistical signal processing, robust stochastic filtering, and machine learning, with applications to positioning systems and wireless communications. He is the recipient of multiple awards including the 2014 EURASIP Best Ph.D. Thesis Award, the 9th Duran Farell Award, the 2016 ION Early Achievements Award, 2019 NSF CAREER Award, and 2022 IEEE AESS Harry R. Mimno Award.






