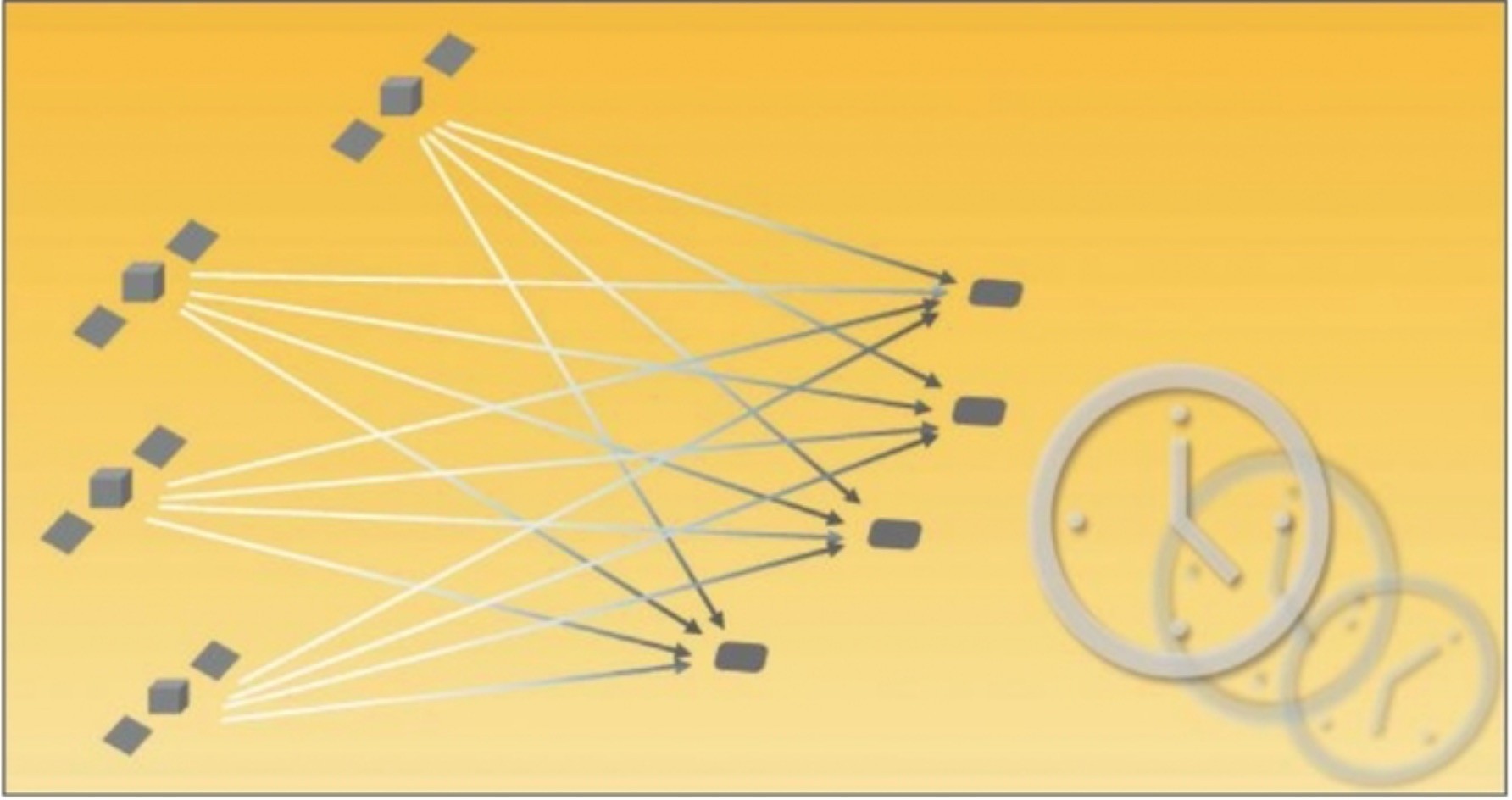
Future telecom, finance and energy sector applications may require time synchronization of tens or hundreds of nanoseconds. A joint time and composite MIMO channel estimation method for indoor receivers can meet these stringent requirements.
GNSS signals used for time synchronization indoors encounter harsh propagation conditions. Wire-based solutions like the precise time protocol (PTP) and commercial solutions based on LEO satellites may be considered as alternative but face other limitations. A solution based on free, open access and globally available GNSS signals, not requiring any additional infrastructure to operate, would be of high interest.
Performance of GNSS indoor timing solutions is driven by the indoor channel propagation conditions. Line-of-sight (LOS) signals may be highly attenuated or completely blocked, and multipath components can introduce significant biases in the timing solution. Commercial timing receivers operating in static indoor conditions may achieve accuracies of the order of hundreds of ns. This limits the direct application of current GNSS receivers to meet the tight time synchronization requirements foreseen in future indoor applications, like small cells for future wireless networks.
To operate in harsh propagation conditions and mitigate the impact of multipath in GNSS receivers, different high-sensitivity architectures and multipath estimation techniques have been proposed, including direct position/time estimators and array-based techniques. These methods still present important limitations in indoor conditions. In particular, high-sensitivity techniques enable the exploitation of GNSS signals in harsh propagation environments, but potentially achieving a limited accuracy. Moreover, trying to estimate multipath components at very low carrier-to-noise density ratio (C/N0) conditions might be very challenging, if not infeasible; and assuming a LOS and one or few multipath components can be far from reality (in practice, diffuse multipath is expected indoors).
Thus, a combination of both high-sensitivity and multipath estimation approaches may be needed to achieve a precise time estimation in indoors.
We present here a joint time and composite multiple-input multiple-output (MIMO) channel estimation approach for static indoor GNSS receivers, featuring an array of antennas. To mitigate the impact of the diffuse (i.e., non-sparse) multipath present indoors, we introduce the concept of composite MIMO channel, targeting the estimation of the aggregated channel contribution of the MN propagation channels (instead of performing individual estimations). To derive a physically plausible and non-sparse channel estimation (required to achieve an accurate and precise estimation of time), Monte Carlo methods assess multiple hypotheses on the structure of the composite MIMO channel. This approach builds on the MIMO-GNSS framework, where multiple GNSS satellites and receiver antennas are jointly exploited for achieving a ubiquitous, accurate and precise PNT solution in harsh propagation conditions.
The MIMO-GNSS Framework
The joint exploitation of the GNSS signals from multiple satellites and/or receiver antennas is not a new topic. Extensive research has been performed in areas like antenna arrays, direct position or collective estimators, and collaborative positioning. Nevertheless, these techniques still face limitations in harsh propagation conditions, and the signal models considered, in particular for antenna arrays, may sometimes be more adequate for mild or controlled conditions than for urban or indoor conditions. Thus, there is still room for improving the exploitation of the transmission and/or reception diversities available.
The MIMO-GNSS framework exploits signal models that allow the robust application of the derived MIMO estimators in realistic harsh propagation conditions. Since the actual signal propagation conditions faced by GNSS receivers can be in practice very complex, simplified signal models allowing the derivation of improved position and/or timing accuracies will be in general targeted.
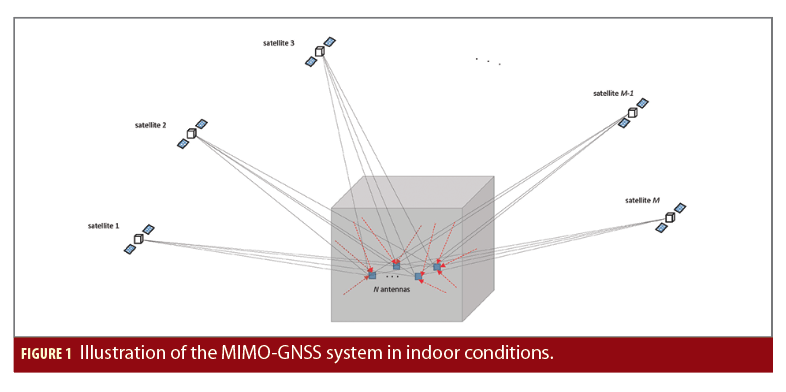
The MIMO-GNSS system for an indoor user is illustrated in Figure 1, where M GNSS satellites and N receiver antennas are considered. Both LOS signals (potentially attenuated or blocked) and multipath components are illustrated. The exploitation of the MIMO-GNSS system has been proposed by the authors for achieving robust unambiguous positioning with high-order BOC signals and for taking advantage of spatial diversity in collaborative positioning. The joint exploitation of all the signals received via multiple antennas allows to improve the ambiguity resolution problem when BOC signals are used thanks to the processing gain and diversity introduced; and allows to improve the positioning accuracy of indoor and/or urban receivers thanks to the better propagation conditions of some of the distributed receivers used in the collaborative solution. In both cases, the usage of a simplified signal model without considering the estimation of the multipath components has shown to be not only appropriate in terms of performance achieved and adaptability to different user scenarios, but also a very convenient approach to reduce the computational burden of the derived solutions. Nevertheless, when a single receiver with multiple antennas is operating indoors, not considering the estimation of multipath results in a biased estimation of time. Based on this, the impact of fading and multipath is proposed to be mitigated in the indoor timing solution via the estimation of a composite MIMO channel embedding the aggregated contribution of all the propagation channels.
Indoor Timing: Signal and System Model
Let us consider a system consisting of a static receiver with N antennas in indoor conditions, all referenced to the same receiver clock; and M GNSS satellites from a certain constellation transmitting navigation signals at a certain carrier frequency and with equivalent correlation properties. Let us assume now that the receiver’s position, the navigation data, and the baseline between each of the N antennas and the receiver’s phase center is known a priori; and that the receiver has performed a coarse clock bias and drift estimation ( and
, respectively) based on state-of-the-art techniques, with
potentially biased due to the impact of the indoor channel. Based on this, the objective now is performing a fine estimation of the receiver’s clock bias (i.e., of the receiver’s time) mitigating as much as possible the impact of the indoor channel.
In general, diffuse multipath with an exponential power delay profile (PDP) of the multipath components is expected in indoor conditions. The LOS signals expected to be received (at least, ideally) from the GNSS satellites are aligned in the clock bias domain (marking the time reference), while diffuse non-LOS (NLOS) multipath components are received with a delay with respect to this time reference to be estimated. This holds true when assuming the receiver’s position and the baseline between antennas are known, as considered herein. In the following, and given the difficulty in practice to model the actual diffuse multipath, let us approximate the LOS and multipath signal components as D components at D discrete time-delays uniformly distributed (with a time-delay resolution Tδ), covering the indoor channel delay spread. Let us also exploit the dependence of the received signal with the clock bias (estimation targeted to be improved), and omit for simplicity the dependence with the clock drift, position, and baseline between antennas (estimated or known a priori). Assuming that the complex amplitudes, time-delays and frequency-shifts of the signal components received are constant during the observation time TsK (note that, in practice, the variations of the time-delays and frequency-shifts can be compensated based on the a priori known or estimated receiver’s position and clock drift), we can approximately model the vector containing a snapshot of K samples (for a sampling period
) of the signal received by the nth antenna of a static GNSS receiver as
where gathers the complex amplitudes for the M LOS contributions;
gathers the complex amplitudes for the M NLOS multipath contributions for the d-th discrete time-delay;
is the complex noise vector (with
); and
is the basis function matrix for the d-th discrete time-delay, which is composed by the M basis function vectors. The m-th basis function vector is defined as
, with the basis function bm
(t-τm,n,0 (δt)–dTδ)exp{j2πfm,n,0t}, where τm,n,0 and fm,n,0 are the time-delay and frequency-shift, respectively, for the LOS signal propagation ray of the m-th satellite received by the n-th antenna; and gm is the complex baseband model of the modulated signal transmitted by the m-th GNSS satellite.
Considering now the later exploitation of the structure of the diffuse channel in the clock bias estimation, let us define the vector containing the coefficients of the composite MIMO channel gathering the aggregated power contribution of the MN propagation channels, such that
is the d-th coefficient of the composite MIMO channel vector. Note that the coefficient h0 corresponds to the contribution of the LOS components, marking the actual receiver’s clock bias to be estimated. The composite MIMO channel gives a measure of the aggregated PDP for the MIMO channel. Each of the coefficients of the composite MIMO channel (one per time-delay) can be considered to follow an arbitrary and unknown probability density function (PDF) which in practice is going to be highly dependent on the indoor environment surrounding the receiver. Indeed, the PDF per coefficient depends on the MN signal contributions received for the corresponding time-delay, with potentially different exponential PDPs for the MN indoor channels, and different attenuations of the LOS components.
MIMO-MLE Time Estimation (Intermediate Estimation)
Under the assumption of only LOS signals being received, we can use the MIMO-MLE to start exploiting all the signals of the MIMO-GNSS system for positioning and collaborative positioning. In this way, the coarse clock bias estimation can be refined, deriving an “intermediate” estimation
of the clock bias as the optimization problem:
where is referred to as the estimated composite MIMO cross-correlation function evaluated for the receiver’s clock bias δt, and ς is a threshold defining the search space around
(expected to be of the order of tens or hundreds of ns, depending on the quality of
).
can be derived as
with the cross-correlations for each of the receiver’s antennas defined as , and
. In practice,
can be approximated as an identity matrix in order to simplify the estimator in (3). Thus, an intermediate clock bias estimation can be obtained based on the coarse clock bias estimation and on the output of the receiver’s correlators by exploiting a multi-correlator architecture. Still, this intermediate estimation can be biased by the impact of the indoor channel, as introduced earlier and will be shown in the simulation results, so the composite MIMO channel estimation is introduced in the time estimation problem in the next section.
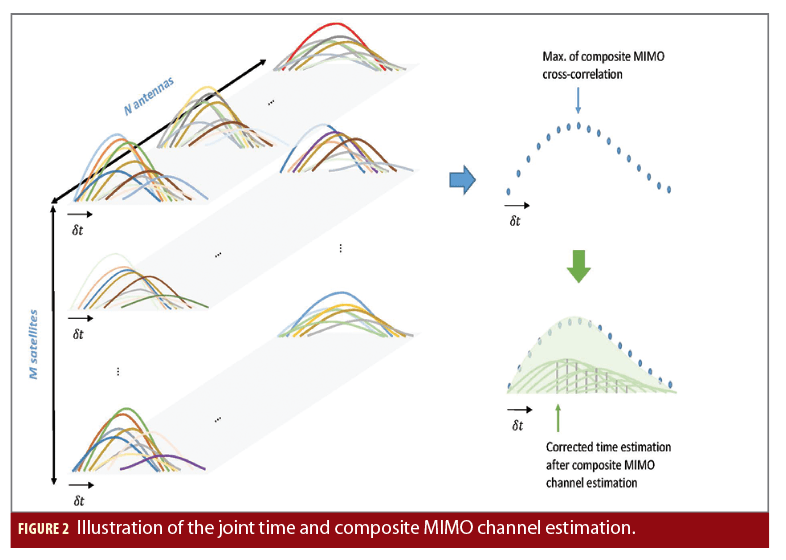
Joint Time and Composite MIMO Channel Estimation (MIMO-JTC Estimator)
The first coefficient of the composite MIMO channel marks the common time-delay of the ideally expected MN LOS signals and, therefore, the receiver’s clock bias. This is the basic concept exploited in the following. It is to be noticed that, due to the impact of the indoor multipath, the first coefficient is expected to be at a certain offset from the maximum of the composite MIMO cross-correlation function (from which the intermediate clock bias estimation
is derived, as shown earlier). Indeed, if no offset would be expected, it would make no sense in the first place to estimate the composite MIMO channel (i.e., the MIMO-MLE would be enough). Taking into account the estimation of the composite MIMO channel using as reference
, the fine clock bias estimation
can be derived as
=
, with
to be jointly estimated with the composite MIMO channel. The joint time and composite MIMO channel estimation is illustrated in Figure 2.
The estimation of the coefficients of the composite MIMO channel is solved as a multi-hypothesis estimation problem in which Nl different PDF assumptions are assessed. Under the l-th hypothesis, the coefficients of the composite MIMO channel are considered to follow the arbitrary set of PDFs
, with pl,dthe PDF for the l-th hypothesis and the d-th coefficient. Based on the previous assumptions, the joint estimator of h and β for the l-th hypothesis can be defined as the solution to the constrained optimization problem:
where , is the miss-modeling error for the composite MIMO channel, which is derived based on the model of the composite MIMO cross-correlation vector Ψ for the h and β assessed, and the estimated composite MIMO cross-correlation vector
(which is uniformly sampling, with a time-delay resolution Tδ, the composite MIMO cross-correlation function Λ(δt) at Q clock bias values, being centered at the intermediate clock bias estimation
, such that
=
; and
constrains the values evaluated for the integer offset β (in total,
values evaluated) based on the expected error of the intermediate clock bias
. In the following, the estimator based on (4) is referred to as the MIMO-JTC estimator, where the estimated values
and
correspond to the hypothesis that minimizes
, out of the Nl PDF hypotheses assessed.
The MIMO-JTC estimator has no analytical solution, so it is proposed to be solved via the application of Monte Carlo methods. In particular, the coefficients of the composite MIMO channel vector h are treated as random variables drawn from the corresponding PDFs (with Nc Monte Carlo runs assessed for each coefficient in each of the NlPDF hypotheses). This approach targets to ensure the derivation of a physically plausible channel estimation (with diffuse multipath components with a certain PDP), avoiding sparse channel solutions with few dominant components (as may be obtained when applying e.g., iterative approaches like SAGE-based algorithms). Additionally, the application of Monte Carlo methods allows a much more efficient implementation than grid-search methods, considered non-practical in the estimation problem treated herein. For the definition of the PDFs, the exponential PDP expected in general for each pair satellite-antenna can be exploited. A simplified PDF model can be used in order to deal with different indoor scenarios and propagation conditions between the MN indoor channels. In particular, under the l-th hypothesis we can define pl,d , where
, d=0,…,D-1, with ηl≥0 the decay rate. With this approach the constraint in the optimization problem in (4) is in practice bounding the set of values that can be considered for each discrete time-delay. Despite the simplicity of this model, this approach allows to substantially improve the clock bias estimation accuracy with respect to the MIMO-MLE estimator, as will be shown later on. Moreover, this model can be adjusted to different indoor conditions by considering different decay rates and/or delay spreads.
Alternative Exploitation of the Spatial Correlation of the Multipath Components (MIMO-JTCC Estimator)
In order to directly exploit the spatial correlation of the multipath components, an alternative joint estimator of h and β can be defined. In this estimator, referred to as the MIMO-JTCC estimator, the composite MIMO channel is derived by minimizing the correlated multipath miss-modeling errors between all the antennas. For the candidate composite MIMO channel vector h being assessed (obtained based on the PDFs pl,d, as for the MIMO-JTC estimator), a multipath miss-modeling error per antenna is to be estimated (similar as for the miss-modeling error for the composite MIMO channel
in (4), but in this case per antenna). Based on
, we can derive a spatial covariance matrix
=
, with
=
…
. The departure from diagonal of
gives a measure of the presence of spatially correlated multipath components not being modeled by the candidate composite MIMO channel vector h. Based on this, in the MIMO-JTCC estimator,
and
correspond to the hypothesis that minimizes
out of the Nl PDF hypotheses assessed, with
measuring the departure from diagonal of
.
Implementation Aspects
The MIMO-MLE, MIMO-JTC and MIMO-JTCC estimators can be derived based on the correlation samples for each satellite-antenna pair; and do not require the array of antennas to be phase-calibrated. Therefore, they are well suited for their implementation at post-correlation level in multi-correlator tracking architectures; and for their application to low-end arrays of antennas. The MIMO-MLE targets the refinement of the coarse clock bias estimation performed by state-of-the-art timing solutions. And the MIMO-JTC and MIMO-JTCC estimators are refining the MIMO-MLE estimation
. Although computationally more demanding than the MIMO-MLE, the MIMO-JTC and MIMO-JTCC estimators will provide the ultimate timing performance by considering the estimation of the composite MIMO channel. Moreover, if we take advantage of the relatively slow temporal decorrelation of the indoor channel expected in general for static GNSS receivers, the proposed estimators can be applied at snapshot level with a certain duty cycle, allowing to limit the computational burden. Additionally, this may also allow the remote processing of the signal snapshots in the Cloud, offloading the local receiver from the processing required by the proposed estimators, while allowing to refine the coarse clock bias estimations. The processing of multiple snapshots may also allow the better modeling of the indoor channel, as well as the exploitation of the indoor channel signature for other applications (e.g., for spoofing detection).
Simulation Results
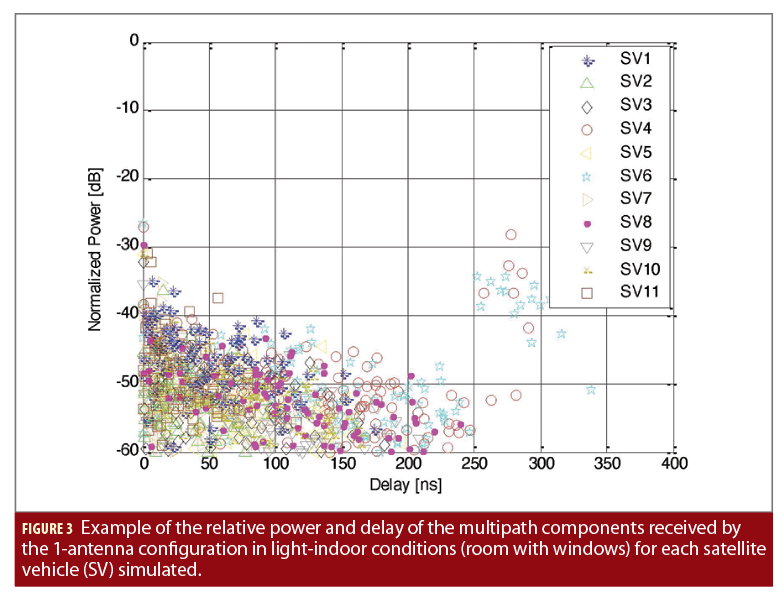
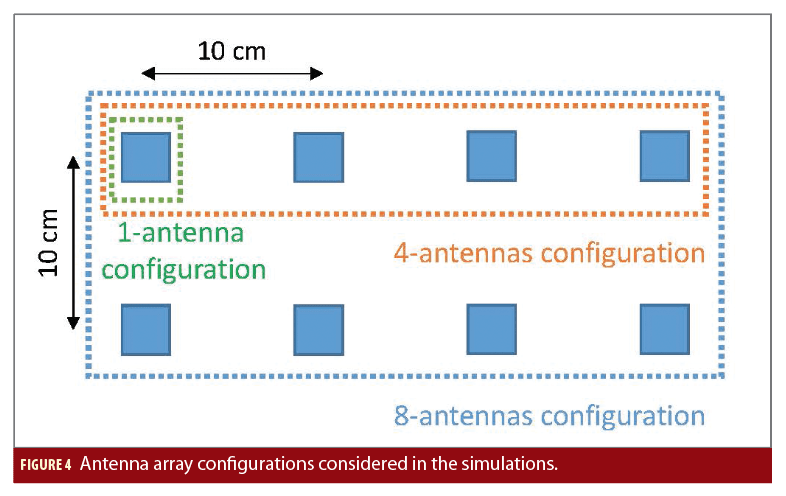
The wideband satellite-to-indoor channel model in the Recommendation ITU-R P.681 has been used to assess the performance of the MIMO-MLE, MIMO-JTC and MIMO-JTCC estimators. Indoor conditions (i.e., a room without windows, with only NLOS signals received), and light-indoor conditions (i.e., a room with windows) have been simulated. Fig. 3 shows an example of the normalized power and delay of the LOS and multipath components simulated. A static receiver with 1, 4 and 8 antennas in the array configuration shown in Fig. 4 is considered. A conventional weighted least squares (WLS) solution is derived as reference for the single-antenna configuration. A single GNSS constellation in a representative geometric configuration transmitting BPSK(1) signals in L1 is considered, together with a receiver with a bandwidth of 5 MHz. For the MIMO-JTC and MIMO-JTCC estimators, only 2 PDF hypotheses considering different channel delay spreads are assessed (i.e., Nl=2), and 10 Monte Carlo runs are considered for each of the two hypotheses (i.e., Nc=10) in order to limit the computational burden of the implemented solutions.
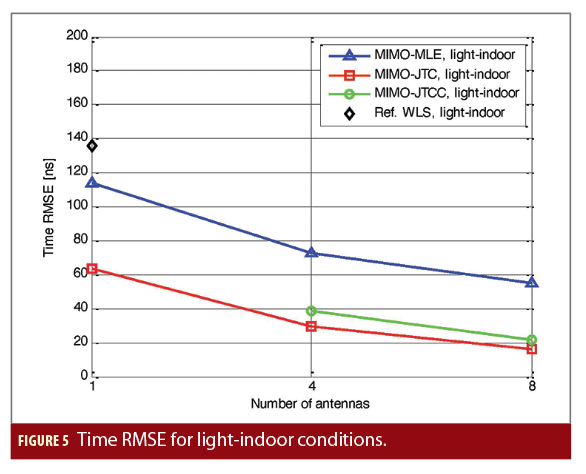
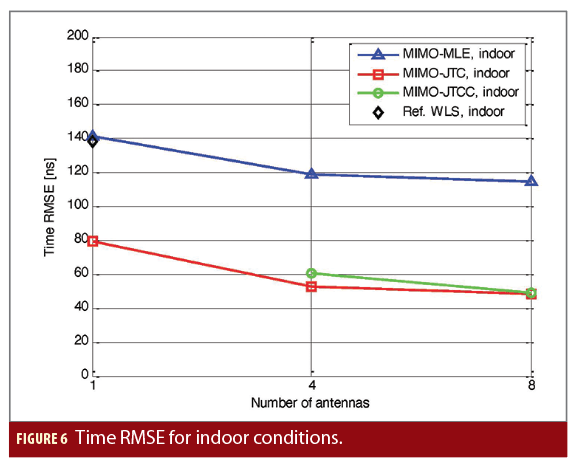
Figures 5 and 6 show the root-mean-square error (RMSE) of the time estimation obtained by the proposed estimators in light-indoor and indoor conditions, respectively, as a function of the number of antennas exploited in the receiver. As can be shown, the spatial diversity introduced by multiple receiver antennas results in an improved timing accuracy for all the proposed estimators. The MIMO-MLE in the single-antenna configuration, corresponding to the conventional direct time estimator (DTE), improves the timing accuracy with respect to the reference WLS solution in light-indoor conditions, while obtaining similar results in indoor conditions. This shows that the DTE solution is not enough to improve the timing accuracy indoors. Thanks to the estimation of the composite MIMO channel, the MIMO-JTC estimator in the single-antenna configuration achieves an important improvement of the timing accuracy with respect to the MIMO-MLE. When 4 and 8 antennas are exploited, the MIMO-JTC and MIMO-JTCC estimators outperform the MIMO-MLE, with the MIMO-JTC estimator obtaining slightly better results than the MIMO-JTCC estimator in all cases. The results obtained show that the simplified hypotheses considered to constrain the estimated composite MIMO channel to physically plausible values are enough to improve the timing accuracy in indoor conditions (even with a relatively low number of Monte Carlo runs used).
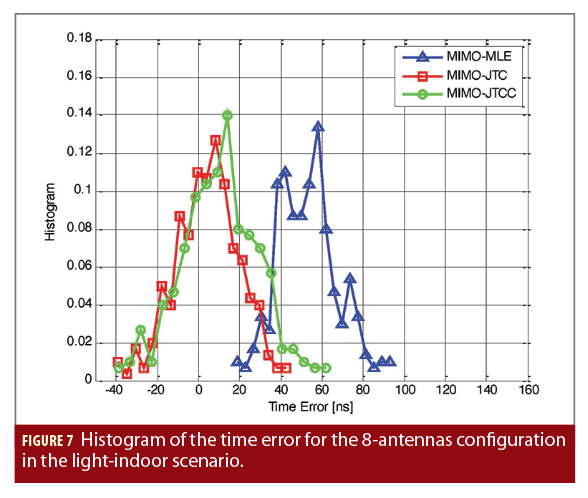
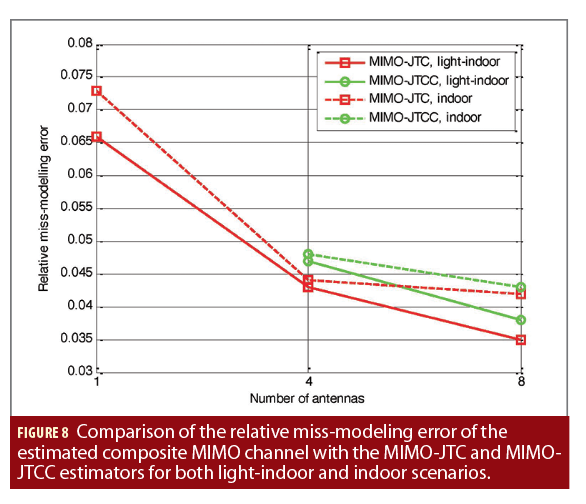
Figure 7 shows a comparison of the histogram of the time error obtained with the MIMO-MLE, the MIMO-JTC and the MIMO-JTCC estimators for the 8-antennas configuration in light-indoor conditions. As can be observed, the MIMO-JTC and MIMO-JTCC estimators reduce the bias introduced by the channel with respect to the MIMO-MLE. This clearly shows the benefit introduced by the estimation of the composite MIMO channel. It can be also observed that the dispersion of the errors is slightly lower for the MIMO-JTC estimator than for the MIMO-JTCC estimator, explaining the lower time RMSE obtained. This can be further explained by the relative miss-modeling errors of the estimated composite MIMO channel obtained for both estimators, as shown in Figure 8. As can be observed, lower channel estimation errors are obtained for the MIMO-JTC estimator than for the MIMO-JTCC in both light-indoor and indoor conditions; and these errors are lower in light-indoor conditions than in indoor conditions, and when the number of antennas increases. These results indicate that the contribution of multipath components spatially not correlated cannot be neglected in the problem. Thus, focusing only on the minimization of the impact of the correlated multipath components between antennas does not result in the best performance (at least for the indoor conditions simulated). Therefore, it appears to be more beneficial to exploit the spatial diversity for improving the equivalent signal-to-noise ratio (SNR) conditions in which the joint composite MIMO channel and time estimator operates, as it is done in the MIMO-JTC estimator.
Conclusions
The indoor time synchronization problem in the MIMO-GNSS framework has been reviewed. The joint time and composite MIMO channel estimation approach implemented in the MIMO-JTC and MIMO-JTCC estimators has shown to outperform the MIMO-MLE in indoor conditions. Moreover, the benefits introduced by the exploitation of spatial diversity indoors have been shown. Timing accuracies below 50 ns (RMSE) are shown to be feasible to be achieved indoors, being the proposed estimation approach an appealing solution for future applications with tight time synchronization requirements like indoor small cells for future wireless networks.
Disclaimer and Acknowledgments
The views presented in this article represent solely the opinion of the authors and not necessarily the view of ESA. This article is based on the material presented in J. A. Garcia-Molina, “GNSS Signal Processing and Spatial Diversity Exploitation,” Ph.D. Thesis, Barcelona, February 2020; and J. A. Garcia-Molina, “Method and Apparatus for Performing Joint Channel and Time Estimation in a GNSS Receiver,” International Patent Application No. PCT/EP2018/063660, WO2019223870A1, May 2018.