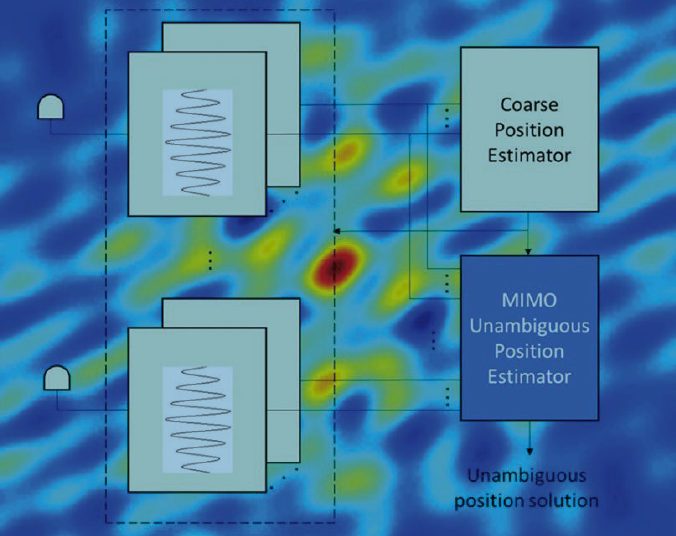
The joint exploitation of meta-signals received from multiple GNSS satellites, and from one or multiple antennas, can achieve high-accuracy PNT solutions in harsh propagation conditions.
The achievement of highaccuracy PNT solutions in harsh propagation conditions is still a challenging problem. Although carrier-based positioning solutions like PPP or RTK can perform very well in mild propagation conditions (e.g., open-sky conditions), the exploitation of carrier-phase observables in urban conditions is not an easy task. Things get even worse indoors. In these harsh propagation scenarios, code-based pseudoranges may still be exploited by GNSS receivers, at the cost of lower PNT accuracies being achievable, with positioning accuracies from few meters to up to tens of meters.
To overcome these limitations, the so-called meta-signal processing of two or more GNSS signal components transmitted in different carrier frequencies may be exploited for deriving high-accuracy code-based pseudoranges. Similar to the case of BOC signals, a narrower main correlation peak than those of the original signals is obtained for the meta-signals, producing a better code-phase estimation. But this is introduced at the cost of multiple correlation peaks appearing in the autocorrelation function. Thus, meta-signal processing implies a potential ambiguity in the code pseudoranges derived, in particular in harsh propagation conditions with low C/N0 conditions, where it can be difficult to distinguish between main and side correlation peaks.
The application of meta-signal processing is of particular interest in propagation conditions in which carrier-based PNT solutions are no longer robust (i.e., for low C/N0 conditions and fading/multipath conditions). Thus it is fundamental to deal with the ambiguity problem in order for the meta-signal processing to provide an actual benefit in the derivation of the PNT solution. For this purpose, the multiple-input multiple-output (MIMO) GNSS framework, already proposed for the unambiguous positioning with high-order binary offset carrier (BOC) signals, can be generalized for the exploitation of meta-signals. This generalized MIMO processing approach consists in the joint exploitation of multiple signals in different carrier frequencies, received from multiple GNSS satellites via one or multiple receiver antennas.
Although a MIMO estimator involves a higher complexity of the PNT solution with respect to state-of-the-art techniques, it can enable the derivation of instantaneous high-accuracy solutions in urban and even indoor conditions. Moreover, it can be shown to be applicable to snapshot and duty-cycling processing approaches. It can also be based on multi-correlator receiver architectures where the MIMO estimator is used to enable an unambiguous PNT solution.
Meta-signal Processing
The meta-signal processing approach was introduced originally by J. L. Issler et alia (see Additional Resources) as a way to achieve high-accuracy code pseudoranges based on the joint processing of two signal components at different carrier frequencies, following the main idea of E5 AltBOC processing, and, in general, of BOC processing. In general, we can consider as meta-signal processing the joint exploitation of two or more signal components. While two components may be exploited to maximize the Gabor bandwidth of the resulting meta-signal, additional signal components may be exploited to obtain an autocorrelation function with better false-lock probability properties. For the case of two signal components, the meta-signal autocorrelation function as a function of the code delay τ can be approximated as
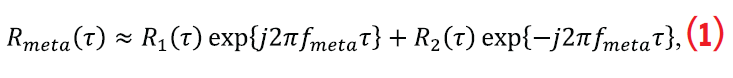
where R1(τ) and R2(τ) are the autocorrelation functions of the signal components used, with carrier frequencies f1 and f2, respectively, and f1>f2; and fmeta is the so-called meta-signal sub-carrier frequency, defined as fmeta=| f1-f2 |/2.
Thus, the selection of the signal components used defines the number of correlation peaks, and their relative power and code delay separation with respect to the main correlation peak. Additionally, due to the potentially different power and/or spectrum of each of the signal components forming the meta-signal, in general the meta-signal autocorrelation function can be complex.
Although a promising approach to achieve high-accuracy PNT solutions, meta-signal processing introduces new problems to deal with. First of all, the two or multiple signal components must be processed maintaining the higher accuracy provided by the frequency separation between them, as obtained from the application of the ideal matched filter to the resulting wide-band signal. For the case of two signal components in some typical receiver architectures, this can be seen analogous to the tracking of the sub-carrier of BOC signals to derive accurate pseudorange estimations.
Additionally, eventual data and/or secondary/overlay codes modulated onto the individual signal components must be wiped off as part of the process. Moreover, the processing of signal components at different or very different carrier frequencies can introduce the need to compensate for the appearance of different delays for each of the signal components due to hardware delays (introduced by the receiver and/or the satellite) and/or ionospheric delays.
The potential different powers and/ or spectrums of each of the signal components also produces the need to deal with complex cross-correlation functions. Finally, meta-signal processing introduces an ambiguity problem in the code pseudorange estimation due to the appearance of multiple correlation peaks in the autocorrelation function, as introduced earlier.
The rest of this article focuses on this ambiguity problem, which has been a challenging problem for many years in the case of high-order BOC signals, and must be dealt with as well in the case of meta-signals to fully exploit the higher accuracy provided. As example of meta-signal processing for the case of Galileo, Figure 1 illustrates the cross-correlation function obtained for Galileo E5 processing (E5a–Q+E5b–Q, with a bandwidth of 50∙f0 MHz; f0=1.023 MHz) and for the meta-signal processing of E5b–Q+E6–C (with a bandwidth of 85∙f0 MHz).
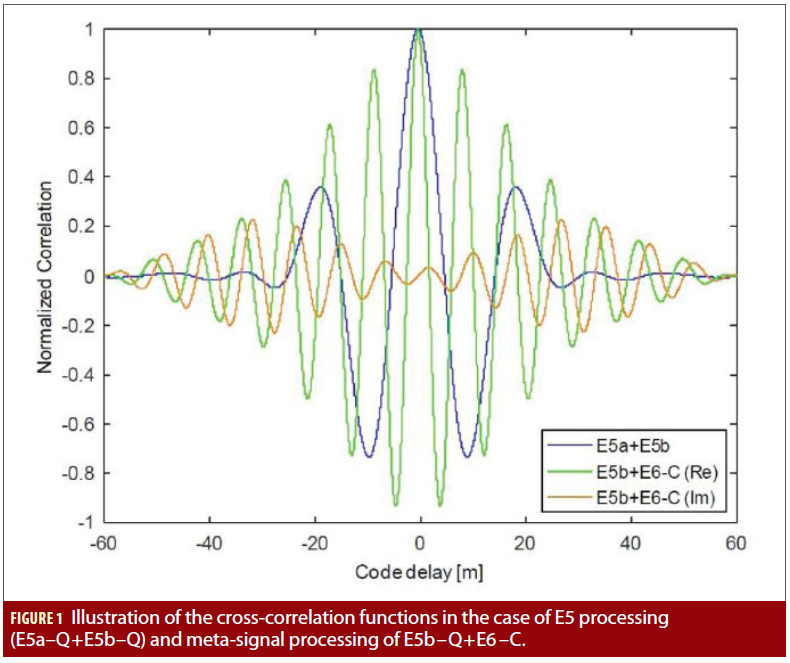
As can be seen, the meta-signal processing of E5b–Q and E6–C introduces a sharper main correlation peak than for E5 processing (which results in better code accuracies being achieved), as well as multiple side correlation peaks close, in power and code delay, to the main correlation peak (which introduces a non-negligible ambiguity problem to be dealt with).
MIMO-GNSS Processing with Meta-signals
The MIMO-GNSS processing targets the join exploitation of GNSS signals from multiple satellites and/or multiple receiver antennas for achieving a ubiquitous, accurate and precise PNT solution in harsh propagation conditions (see J.A. Garcia-Molina 2020 in Additional Resources). This joint exploitation of multiple signals is performed in the position and/or time domain, equivalently to direct position/time or collective estimators in the case of single-antenna receivers.
The application of the MIMO maximum likelihood estimator (MIMOMLE) for the derivation of unambiguous position solutions has shown promising results when high-order BOC signals are exploited (see J.A. Garcia-Molina et alia 2019 in Additional Resources). Similarly, the MIMO processing can be applied to the unambiguous exploitation of meta-signals to achieve high accuracy PNT solutions. In this case, the ambiguity problem can be treated directly in the position domain (and/or in the time domain) instead of at pseudorange level.
This means that, instead of trying to identify separately which one is the main correlation peak for each WORKING PAPERS of the meta-signals being exploited, the target is to directly identify in the position domain the local maximum corresponding to the main correlation peaks (i.e., corresponding to the actual position of the receiver). Thanks to the different geometries of the GNSS satellites with respect to the receiver (i.e., to the transmission diversity), this allows a more robust unambiguous positioning.
Note that the contributions of the main correlation peaks in the position domain are aligned for the actual receiver’s position, while the contributions of the side correlation peaks are not necessarily aligned for other positions being assessed. Therefore, the difference of magnitude between the global maximum and the local maximums in the position domain is expected to be in general larger than the difference between the main correlation peak and the side correlation peaks in the cross-correlation function of the individual signals. Figures 2 and 3 illustrate the contribution of the multiple signals in the horizontal position domain for the case of E5 processing and for the meta-signal processing of E5b– Q+E6–C, respectively.
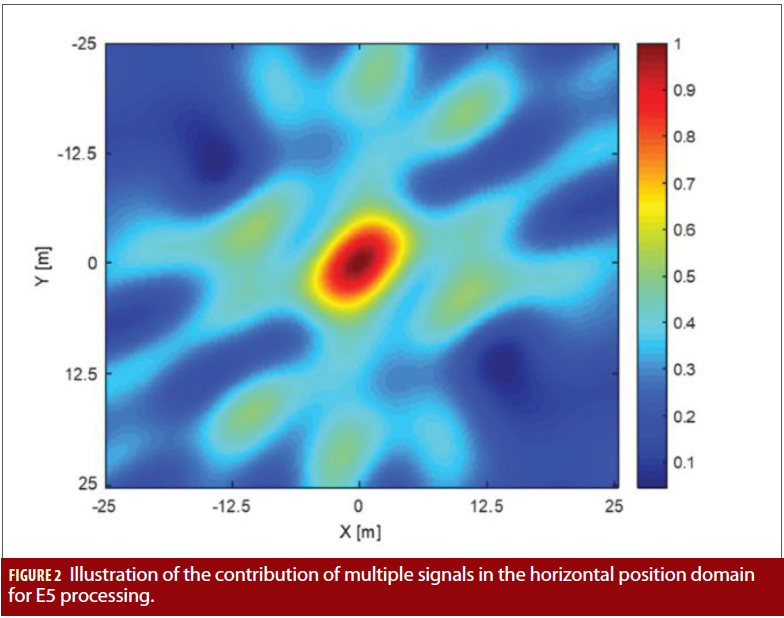
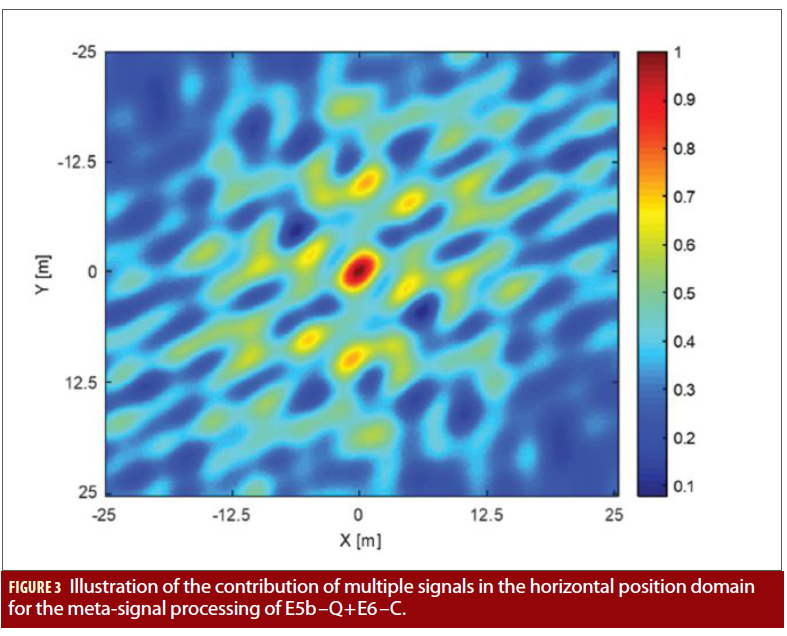
As in the case of high-order BOC signals, the unambiguous positioning problem with meta-signals is proposed to be treated as a fine estimation problem in which a coarse position solution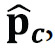 
is a priori available (e.g., a position solution derived based on potentially ambiguous pseudoranges estimated with conventional tracking techniques, or derived based on pseudorange estimations for one of the individual signals). This allows bounding the estimation problem, drastically reducing the complexity of the implementation of the MIMO-MLE with respect to the typical exploitation of direct positioning and collective detection techniques. It also allows application of the MIMOMLE based on state-of-the-art multi- correlator architectures. Considering a MIMO system with M satellites and N antennas, with Po the receiver’s phase center position to be estimated and 
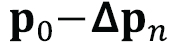defining the position of each of the receiver’s antennas, the MIMOMLE can be derived as the constrained optimization problem
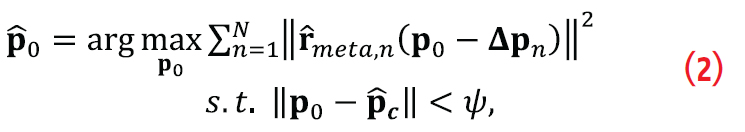
where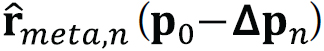 
contains the M estimated meta-signal cross-correlation samples (one per satellite) for the current evaluated position po and the nth antenna; and ψ bounds the search area around .
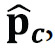Due to the high accuracy provided by the meta-signals (which can be in the order of, or below, the separation between the receiver’s antennas), the narrowband array model typically used with arrays of antennas is not considered by the MIMO estimator, which explains the introduction of ▵pn. Moreover, the estimator does not target the spatial filtering of the colored noise that may be introduced by multipath, since the meta-signal processing by itself is a way to deal with multipath (and, in any case, the spatial filtering of multipath in harsh propagation conditions is a challenging problem in practice).
The proposed solution assumes that the cross-correlations between the GNSS signals from different satellites can be considered approximately null, which simplifies the optimization problem. In the case of a single-antenna receiver, the multiple-input single-output (MISO) MLE is derived as for the MIMO-MLE with N=1.
Consider now a receiver with a multi- correlator architecture, such that a partial or complete uniform sampling of the cross-correlation function for each satellite and antenna is performed with enough resolution (i.e., enabling the reconstruction of the cross-correlation function for the bandwidth exploited). Assume that the prompt correlation samples are driven by the coarse position 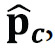, and that a continuous cross-correlation function 
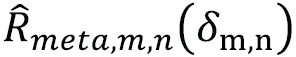is derived per satellite and antenna by interpolation of the corresponding estimated cross-correlation samples (with 
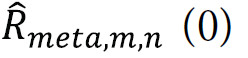corresponding to the prompt correlation sample). In this case, can be derived for each evaluated position as = 
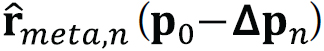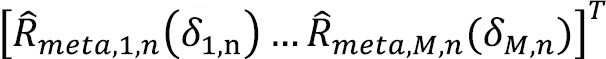, with 
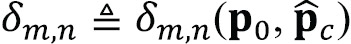the expected pseudorange difference for the mth satellite and nth antenna introduced by the change in position from 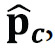to .
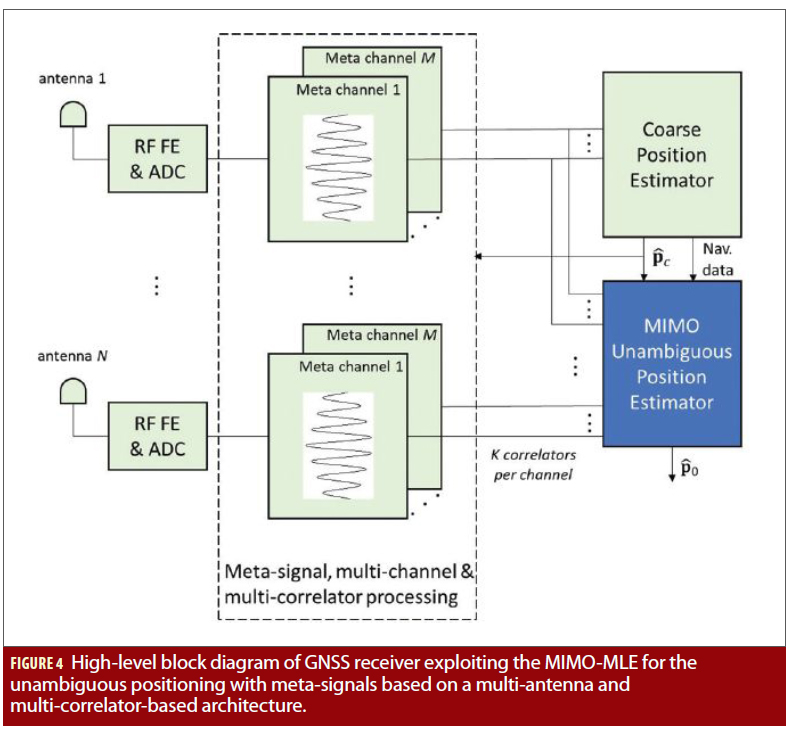
Figure 4 shows the high-level architecture of a multi-antenna and multi-correlator- based GNSS receiver exploiting the MIMO-MLE for the unambiguous positioning with meta-signals. This architecture can be easily adapted to the single-antenna case, in which case the MISO-MLE is to be used for the unambiguous positioning.
Meta-signal Performance
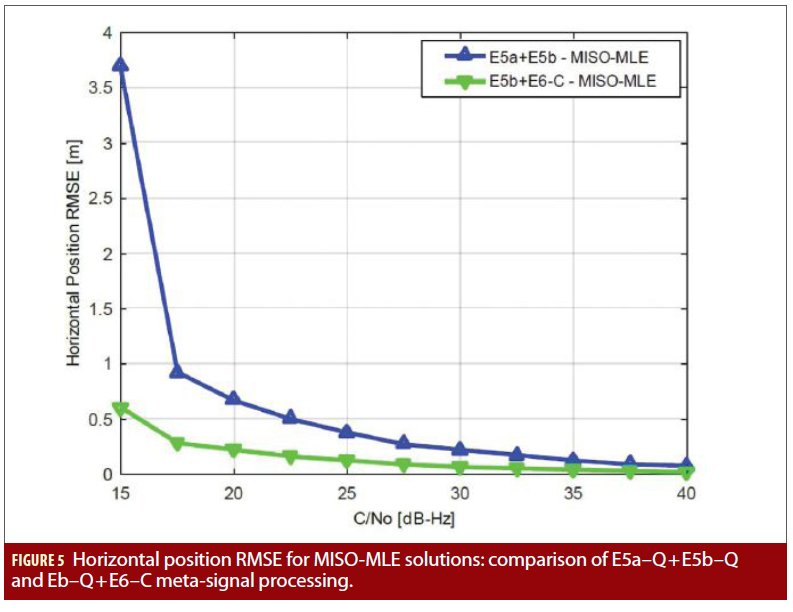
Let us start looking at the positioning performance provided by meta-signal processing by comparing the horizontal position root mean square error (RMSE) achieved by the processing of Galileo E5 (E5a–Q+E5b–Q) and the meta-signal processing of E5b–Q+E6–C, as shown in Figure 5. In both cases, a single-antenna receiver exploiting the MISO-MLE estimator is considered and the results are shown vs. the C/N0 (assumed equivalent for all the satellites for simplicity) when considering a coherent integration period of 100 ms. The scenario considers a horizontal dilution of precision (HDOP) equal to one, and no additional system or atmospheric errors are introduced. As expected, the meta-signal processing of E5b–Q+E6–C allows a substantial improvement of the achieved accuracy with respect to E5 processing (e.g., for 25 dB-Hz, the horizontal position RMSE for E5 processing is around 0.4 m, while it is around 0.1 m for the meta-signal processing of E5b–Q+E6–C).
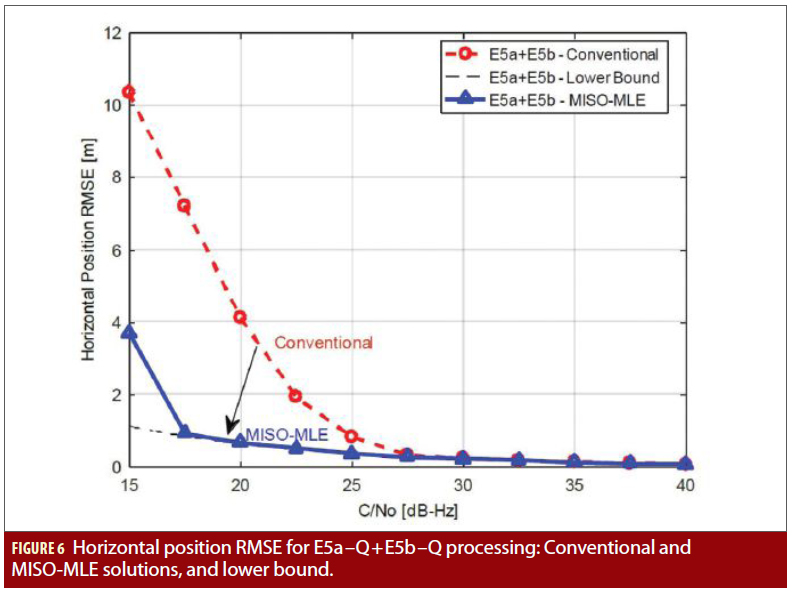
The previous results show what we can achieve with meta-signal processing when the meta-signals are jointly exploited in the position domain by the MISO-MLE (or by the MIMOMLE in the case of multiple antennas), dealing with the ambiguity problem in the position domain. But in case a conventional processing approach is considered (i.e., the receiver is dealing with the ambiguity problem at ranging level for each meta-signal and performing the position solution based on the derived pseudoranges) the result obtained is different. To show this, the MISO-MLE solution is compared to a conventional processing approach in which the MLE at pseudorange level (based on a multi-correlator architecture) is applied to solve the ambiguity for each meta-signal.
Figure 6 shows the comparison of the horizontal position RMSE for the case of E5 (E5a–Q+E5b–Q) processing, while Fig. 7 shows the results for the meta-signal processing of E5b–Q+E6–C. For the case of E5 in Figure 6, the conventional solution attains the lower-bound of the position error down to around 27 dB-Hz (resulting in errors above the meter below around 25 dB-Hz), while the MISO-MLE attains the lower-bound down to around 17 dB-Hz (with errors below the meter down to around 17 dB-Hz).
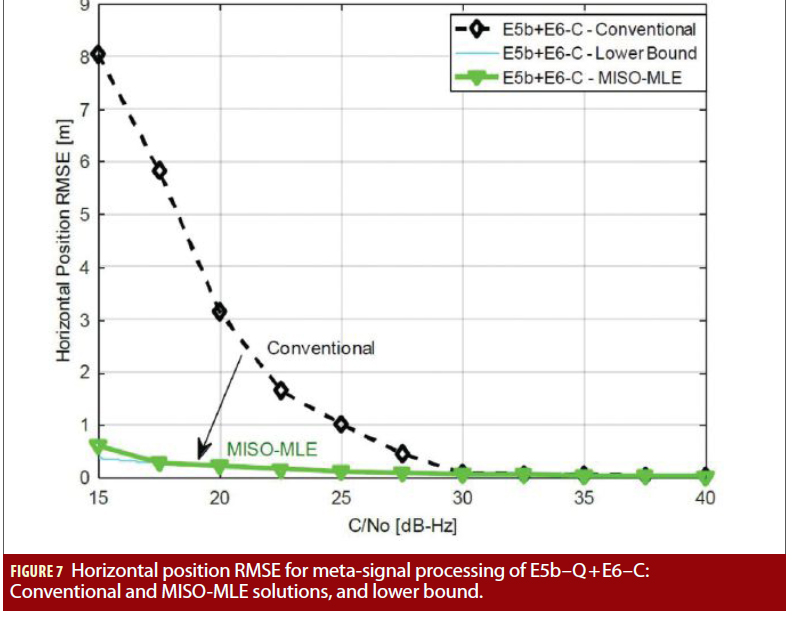
The performance degradation of the conventional solution with respect to the MISO-MLE (and with respect to the lower bound) is introduced by the higher impact of the false-locks when the ambiguity resolution is performed at pseudorange level. This shows that low C/N0 conditions are enough to introduce problems with the ambiguity resolution and limit the actual benefit introduced by meta-signal processing in conventional receiver architectures.
Similar conclusions are obtained from the meta-signal processing of E5b–Q+E6–C in Figure 7. In this case, the conventional approach starts suffering the impact of false-locks below around 30 dB-Hz. In this case the side correlation peaks of the meta-signal autocorrelation function are very close in power and code delay to the main correlation peak, as shown in Figure 1, so the impact of false locks in the conventional solution is important. On the contrary, the MISO-MLE is able to deal with the ambiguity problem down to around 17 dB-Hz, achieving errors below the meter down to 15 dB-Hz.
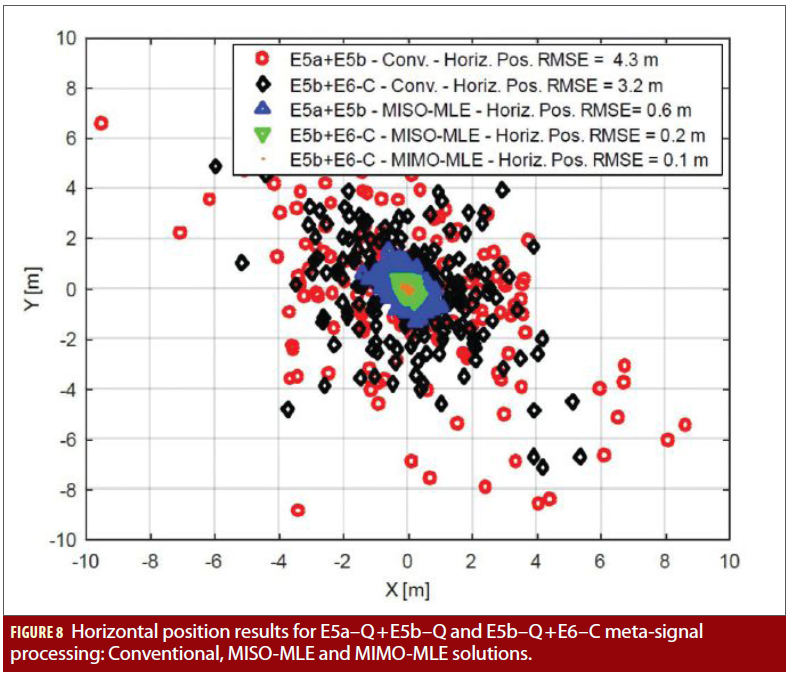
A comparison of the horizontal position results obtained for the conventional approach, the MISO-MLE, and the MIMO-MLE (with 4 antennas) is shown in Figure 8 for low C/N0 conditions (20 dB-Hz). Looking in particular to the meta-signal processing of E5b– Q+E6–C, the horizontal position RMSE for the conventional approach is around 3.2 m; for the MISO-MLE the position error goes down to 0.2 m; and it goes down to 0.1 m when the MIMO-MLE is exploited to deal with the unambiguous processing of the meta-signals.
Conclusions
The ambiguity problem must be dealt with for meta-signal processing to provide an actual benefit in the derivation of PNT solutions in harsh propagation conditions where low C/N0 conditions are present. This is proposed to be performed directly in the position domain, exploiting the MISO-MLE and MIMOMLE meta-signal solutions. This allows improving the unambiguous positioning with meta-signals with respect to the usage of conventional ambiguity resolution techniques at ranging level.
Further work is to be performed, in particular for indoor conditions, where the MISO-MLE and MIMO-MLE meta-signal solutions are expected to enable the achievement of sub-meter accuracies. This can be extended as well to timing applications, where meta-signal processing is also considered of high interest.
Authors
J. A. García-Molina is a radio navigation engineer at the European Space Agency (ESA), where he leads the Galileo 2nd Generation (G2G) Signal- In-Space Team and G2G receiver design activities. He also leads R&D projects and internal research activities on signal processing techniques for positioning and timing in harsh propagation conditions. He actively participates in the EU’s Compatibility, Signal and Interoperability working group, and represents ESA in the European GNSS Interference Task Force. His research interests include MIMO-GNSS signal processing for indoor/urban positioning and timing, Cloud-GNSS and collaborative signal processing, acquisition and fasttime- ambiguity-resolution signals, and unambiguous estimation of high-order BOC signals and meta-signals.
