GNSS positioning is premised on the idea that the satellite positions are known, or can be calculated. Errors in the computed satellite position will manifest as ranging errors that degrade the positioning accuracy.
It is important, therefore, to ensure satellite orbit calculations are as accurate as possible. As discussed in this article, Earth rotation plays a key role in this regard but surprisingly few references on orbit calculation actually mention its affect explicitly or how to compensate for it. Don’t fret, however, the correction is certainly applied or positioning accuracy would be much worse than is currently attained.
Reference Frames
Earth rotation is important because of the choice of reference system in which orbital calculations are performed. In particular, GNSS orbits — either from the broadcast orbital models or precise post-mission estimation — are parameterized in an
Earth-Centered Earth-Fixed (ECEF) coordinate frame such as the WGS84 reference frame used for GPS.
A common definition of an ECEF frame is one whose z-axis is the rotational axis of the Earth (pointing north), whose x-axis is in the equatorial plane and includes the median passing through Greenwich, and the y-axis completes the frame (typically in a right-handed sense). By definition,such a frame rotates with the Earth and is thus time-varying in inertial space with a period of 24 hours.
In the context of satellite position computations, this means that satellite locations can be computed at any given time, in an ECEF coordinate frame that is valid at that same time.
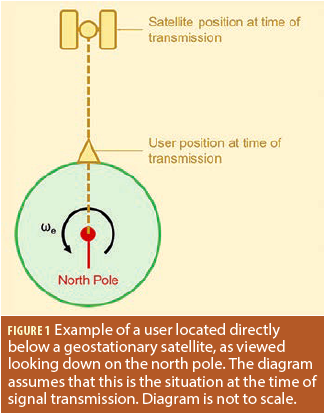
An easy way to visualize this point is to consider an ideal geostationary satellite whose position relative to the Earth does not change over time — orbital parameters or orbital files would always yield the same coordinates for the satellite.
Effect of Earth Rotation
So where does Earth rotation enter the picture? Well, precisely from the fact that the time at which a satellite transmits a signal, and the time a receiver receives that signal differs. Between the time of transmission (tt) and the time of reception (tr) — roughly 70 milliseconds (give or take few milliseconds) for medium-Earth orbiting (MEO) satellites — the Earth has rotated by ωe . (tr – tt), where ωe is the rotation rate of the Earth.
To illustrate the effect of this, we return to our idealized geostationary satellite. We further consider a user located directly below the satellite. Figure 1 shows this situation looking down on the north pole. To simplify later discussions, we consider this figure to apply at the time of signal transmission.
Since the orbital radius of a geostationary satellite is known (approximately 42,164 kilometers) and the radius of the Earth is known (approximately 6,371 kilometers) the separation of the user and satellite at any given instant is constant and can be easily computed.
Now consider Figure 2, which shows the same figure but also includes the location of the user and satellite at time of signal reception. Because of Earth rotation, the signal travels the path denoted by the blue line, which is obviously longer than the instantaneous separation of the satellite and user. This is the path in inertial space (ignoring the Earth’s orbit around the sun for simplicity).
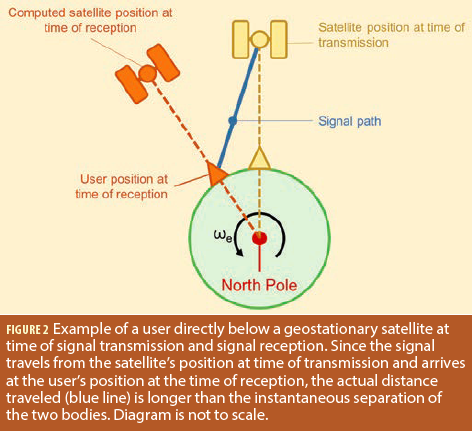
The problem, however, is that because orbits are parameterized in an ECEF frame, the computed position of the satellite will still be directly above the user. This leads to a situation where the true signal path and the computed signal path differ. Unless accounted for, this difference will manifest as a ranging error in the receiver’s position engine, which computes the difference of the measured and predicted signal paths (i.e., ranges). The magnitude of the position error depends on the number and distribution of satellites, as well as user latitude. As an example, in Calgary, Canada, ignoring Earth rotation results in a shift in the estimated user position of about 20 meters, primarily in the east/west direction.
Before moving on, although we used the example of a geostationary satellite, the exact same effect applies to non-geostationary orbits as well. The main difference is that the satellite positions in Figures 1 and 2 would not necessarily be directly above the user, and the distance between the user and satellites, projected into the equatorial plane (which is shown in Figures 1 and 2), will vary with time as satellites move along their orbits. The good news is that regardless of the orbit, the method of compensation is the same.
Simple Solution
To remove the discrepancy between the measured and computed signal paths, we need to compute the ECEF position of the satellite at the time of transition in the ECEF frame at the time of signal reception. Fortunately, this is easily accomplished by realizing that the two coordinate frames are related by a rotation about the z-axis.
Mathematically, we can write
![]()
where is a position vector at the subscripted time (or frame), and R3 (ωe . (tr – tt)) is the rotation matrix about the z-axis by the angle subtended by the Earth rotated during signal propagation.
Applying the transformation in (1) yields the position of the yellow satellite in Figure 2, which allows for the proper computation of the (orange) user position.
The astute reader might be wondering how the propagation time is computed. This can be found by iterating to a solution: first, assume an initial distance between the user and satellite (e.g., 70 milliseconds); then compute the satellite position using this assumed distance (for Earth rotation compensation); use the approximate user position to re-compute the range to the satellite; and finally use this range to compute the satellite position.
The accuracy of the user position in the iteration is not typically a problem. The reason is because, even with a position error of 10 kilometers, the worstcase propagation time error would be 33.3 μs (i.e., 10 km / 3e8 m/s). Multiplying this by Earth rotation rate (~7.3e-5 rad/s) yields an angular error of about 2.4 nanoradians. Even over an orbital radius of 26,000 kilometers (assuming a MEO orbit), the orbital error is less than a decimeter. Then, of course, after the first epoch, the position error is typically several orders of magnitude smaller making the effect of user position error negligible.
Summary
This article has shown why Earth rotation needs to be accounted for when computing satellite coordinates for GNSS applications. The compensation is simple but crucial steps for obtaining the highest possible positioning accuracies.