TRANSIT on Steroids: Doppler-Based GNSS Meets Large LEO Constellations

An experienced GNSS colleague, soon to be inducted into the National Academy of Engineering, insisted that she had looked into that and found that it does not work. The proponent was not dissuaded. The moderator of the meeting, a potential funder with deep pockets, seemed to like the GNSS newbie’s enthusiasm and awarded him a contract. He hedged his bets, however, by asking this paper’s first author to do some analysis.

This was not our author’s first LEO/Doppler-nav rodeo. He had been one of the chief analysts of the High-Integrity GPS (iGPS) project as a founding member of Coherent Navigation. That project had as its goal exploiting accumulated delta range from Iridium L-band signals in order to augment GPS. Recall that accumulated delta range equals beat carrier phase multiplied by nominal wavelength, and that beat carrier phase equals the (negative) time integral of carrier Doppler shift. Iridium signals use time-division and frequency-division multiple access. Carrier Doppler shift is the most reliable observable, and beat carrier phase is reconstructed by a process that involves cycle-slip estimation during each 81.72 msec dead-time interval between 8.28 msec signal bursts.

The iGPS project sought to do several important things, some military, some commercial. It had some successes. None of them involved stand-alone navigation based purely on Iridium signals. Rather, it always sought to use Iridium signals in concert with GPS signals in ways that would leverage the advantages of each.

A spin-off of the iGPS project had different ideas. It was never exactly clear why Boeing, the iGPS prime contractor, set up an independent effort to do stand-alone navigation based on Iridium signals. Perhaps the company wanted to hedge its bets in case the aggressive goals of the main iGPS program proved too ambitious. In hindsight, Boeing’s spin-off decision proved wise. The main iGPS program was cancelled; Coherent Navigation was absorbed by Apple without reducing any LEO-based GNSS technology to operational practice. The spin-off survived to become Satelles, Inc. Today it offers a viable product based on stand-alone Iridium Doppler- and pseudorange-based navigation.

Satelles’ success does not contradict the rising NAE member’s misgivings about LEO navigation. Satelles claims 20 m accuracy for a static receiver [1]. If motion is involved, then things deteriorate, as our first author knows from experience, even when using an inertial navigation system (INS).

The problem with navigation based on one LEO satellite is geometric dilution of precision (GDOP). This becomes clear if one considers accumulated delta range, which is nominally equivalent to Doppler shift in its ability to provide navigation information. Suppose one makes the optimistic assumption that the accumulated delta range bias can be estimated exactly without degrading the navigation solution. Then the accumulated delta range becomes like pseudorange. As a satellite traverses the sky, it sweeps out a range of locations relative to the receiver. A non-infinite GDOP results only if the multiplicity of locations of the satellite during the pass produces a good geometry. This does not happen.

If the Earth did not rotate, then the satellite-to-receiver direction vectors would all lie in a single plane, and GDOP would be infinite. The Earth’s rotation prevents this, but the resulting GDOP values can be in the hundreds. On paper, this GDOP value can be reduced by taking a large number of samples N, which introduces a 1/√N effect, but measurement error correlations act to blunt the beneficial impact. The precision of beat carrier phase data helps somewhat, but the need to estimate the beat carrier phase bias adds further degradation. Position estimation for a static receiver is possible, as Satelles has demonstrated, but receiver clock drift during a satellite pass makes for complications.

If the receiver is moving, then navigation becomes much more challenging, and accuracy degrades. This happens even when INS data are used to augment the LEO data. The optimistic GNSS novice in the debate planned to use an INS to make things work well for a moving receiver, as did the iGPS program. “Use an INS” seems to be a one-size-fits-all panacea for radio-navigation systems that suffer from poor observability. Sometimes it works, but the incorporation of INS data offers challenges. Even with a very stable INS, there is the added problem of estimating initial velocity, initial attitude, especially yaw, and INS biases.

With a perfect INS (zero velocity and angular random walk, zero bias drift) and a nearly perfect clock (initial frequency uncertainty of 10-9 seconds/sec with zero frequency drift) the per-axis RMS position errors can exceed 40 m after a 10-minute satellite pass. For a realistic INS and receiver clock, the per-axis navigation errors can exceed 1 km RMS. Addition of pressure altimeter and magnetometer data may reduce RMS per-axis errors to several hundred meters. If the navigation system sees multiple satellites often enough, especially in more than one orbital plane, then accuracy improves markedly.

Enter Large LEO

The advent of large LEO constellations is a game-changer. They could remove the drawbacks of LEO-based navigation in general and Doppler-based navigation in particular. A key feature of large LEO constellations is their potential to allow simultaneous measurement of Doppler shifts from a large number of satellites. In order to understand why satellite number is important, consider the form of the following carrier Doppler shift measurement model:

The quantity λ is the nominal carrier wavelength, Dj is the measured carrier Doppler shift from the jth satellite, is the unit direction vector pointing from that satellite to the receiver, is the receiver velocity, is the satellite velocity, δj is the satellite transmitter clock offset, Tj is the true satellite transmission time, δRis the receiver clock offset, TR is the true receiver time, is the neutral atmosphere delay (mainly due to troposphere), is the time-equivalent ionospheric carrier phase advance, and is a term that arises due to Earth rotation during signal propagation.

This equation, or one very much like it, is normally used to estimate receiver velocity and receiver clock offset rate based on carrier Doppler shift from 4 or more satellites if one already knows receiver position and clock offset δR from a pseudorange solution. Often the neutral atmosphere and ionosphere terms are neglected during velocity estimation.

The dependence of the terms , , and on position and receiver clock offset δR is a liability when using carrier Doppler shift for velocity estimation, but it is an asset when using Doppler shift for determining and δR. The challenge for position estimation based on Doppler shift is the inability to estimate it independently of velocity. In fact, one must estimate all 8 unknown elements of the vector simultaneously if carrier Doppler shift is the only observable. This requires the measurement of carrier Doppler shift from a minimum of 8 satellites, just as pseudorange-based navigation requires the measurement of pseudorange from 4 or more satellites in order to estimate and δR simultaneously.

Such a scheme was unthinkable in the past, even in the recent past. No LEO constellation could guarantee simultaneous visibility of 8 or more satellites. TRANSIT only afforded one visible satellite at a time, and had visibility gaps [2]. Iridium can only guarantee that one satellite is visible at all times. A typical receiver can see two satellites about once every 10 minutes, and two satellites are visible nearly all the time if the receiver sits equidistant between two orbital planes. The latter situation might give rise to simultaneous visibility of 3 or 4 satellites once every 10 minutes or so. No Iridium receiver will ever see 8 satellites simultaneously, except near the Earth’s poles.

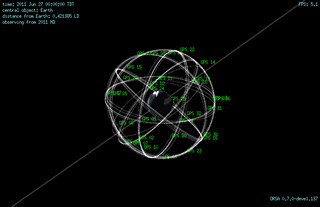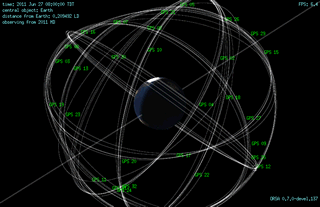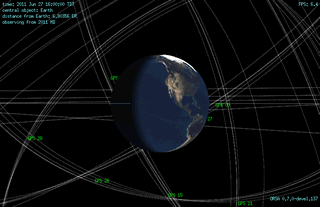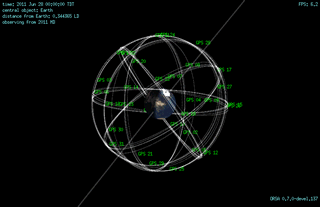
The planning and launch of large LEO constellations such as OneWeb, Starlink, and Kuiper have changed all of this. These constellation designs consist of nearly a thousand to several thousand LEO satellites. Although each satellite is visible to a smaller portion of the Earth than a typical MEO GNSS satellite, there are enough of them to make up for the per-satellite coverage loss. A proposed version of OneWeb’s initial 720-satellite constellation, depicted in Figure 1, will offer simultaneous visibility of 20 or more satellites above a 7.5° elevation mask worldwide. A proposed version of Starlink’s final constellation will yield a minimum of 81 visible satellites above a 7.5° elevation worldwide. These numbers make the use of carrier Doppler shift feasible.

One might consider pseudorange-based navigation from large LEO constellations, but there are two reasons why the sole use of carrier Doppler shift is attractive. First, Doppler shift navigation is less sensitive to transmitter clock errors. It is sensitive only to transmitter clock frequency knowledge errors, and it might be tolerant of errors on the order of 10-11 sec/sec. This obviates the need for atomic clocks. The system could work with good quartz oscillators on the satellites and without GPS disciplining. Second, Doppler shift navigation does not require the satellites to broadcast precise ranging codes. The only signal requirements are (a) that modulated data can be wiped off by the receiver to allow measurement of Doppler shift, and (b) that the receiver be able to distinguish signals from different satellites.

Giving up on pseudorange might seem unwise because of the robustness of pseudorange point solutions. There is no need for any dynamic model, any INS data, or any other data when implementing standard GNSS pseudorange point solutions. A simple Gauss-Newton nonlinear least-squares solver of 4 or more pseudorange equations for the 4 unknowns in yields a reliable navigation fix.

Surprisingly, the same holds true for Doppler-based navigation that uses the equation given above. It too admits point solutions via nonlinear least-squares solution of a system of 8 or more carrier Doppler shift equations for the 8 unknowns in . The needed calculations are more complex than for the pseudorange equations, but they can be implemented with a reasonable amount of effort. The details of how this is done and simulation test results for a point-solution algorithm are presented in [3].

Performance Evaluation

A key question about this concept is its potential accuracy, which can be characterized by the point solution batch filter’s computed covariance matrix. For a pseudorange point solution, a simplified approximation of the corresponding error covariance matrix leads directly to the concept of GDOP as an accuracy metric. There exists a 4×4 non-dimensional geometry matrix whose trace’s square root equals GDOP. The error covariance matrix for the estimate equals the product of this geometry matrix and the variance of the pseudorange measurement error.

Covariance analysis of LEO/Doppler-based navigation systems typically does not admit a simple GDOP metric. When using an INS and a time series of data, there is much more going on than the simple geometry of the line-of-sight vectors from the satellites to the receiver. Estimation practitioners do not like being asked, “What is GDOP?” in such situations, but the question does get asked. It is unanswerable, and the naiveté of the questioner precludes the possibility of explaining why.

For a Doppler-only point solution, however, the question can be asked and answered, but it presents more of a challenge than for a pseudorange point solution. The answer employs an approximation of the point solution’s error covariance matrix [3]. The key equation for developing a sensible GDOP metric is a linearized approximation of the Doppler shift measurement model. It yields the following relationship between measurement errors and estimation errors:

where N is the number of satellites, ΔDj is the Doppler shift measurement error for the jth satellite, Δ is the position error, ΔδR is the receiver clock offset error, Δ is the velocity error, and is the receiver clock offset rate error. The N×8 non-dimensional “geometry” matrix in this equation is

It uses the following two factors to nondimensionalize its first 4 columns:

The quantity γ has units of radians/sec and is the maximum possible magnitude of the angular sweep rate of a line-of-sight unit direction vector as viewed by a receiver on the surface of a non-rotating Earth if the satellite is in a circular Keplerian orbit with a semi-major axis . The quantity RE is the Earth’s radius. The quantity η has units of m/sec2. It is the maximum possible range acceleration due to satellite motion between a receiver on a non-rotating Earth and a satellite in a circular Keplerian orbit of semi-major axis .

The 8 elements of the vector of estimation errors on the right-hand side of the linearized Doppler shift error equation, , all have units of m/sec, as does the vector of range-rate-equivalent Doppler shift measurement errors on the left-hand side of the equation, . If the carrier Doppler shift measurement errors are uncorrelated and if they all have the common variance , then a good approximation of the filter’s computed estimation error covariance matrix for is . A sensible GDOP for this system is

The corresponding estimation precisions are meters for the components of , seconds for meters/sec for the components of , and seconds/sec for .

This GDOP analysis indicates several important properties that are needed for good system accuracy. A low GDOP is important for all of the estimated quantities’ accuracies. A large γ, i.e., a large maximum possible angular sweep rate of the satellite-to-receiver line-of-sight vectors, is important to this concept’s position accuracy. A large η, i.e., a large maximum possible range acceleration between the satellite and the receiver due to satellite motion, is important to the method’s clock offset accuracy. Examination of the matrix demonstrates the importance of good line-of-sight vector geometric diversity in order to have a low GDOP, as for traditional pseudorange-based GDOP. In fact, the last 4 columns of the matrix are identical to the entire GDOP matrix of a pseudorange analysis. These columns, however, apply to the velocity and clock offset rate terms when using carrier Doppler shift measurements. The first three columns of indicate the importance of the geometric diversity and magnitudes of the line-of-sight vector’s time derivatives, for j=1,…,N. The fourth column indicates the importance of large magnitudes and a diversity of signs for the satellite-motion-induced part of the range acceleration between the satellite and the receiver. Figure 2 depicts example satellites, their orbits, their vectors, and their vectors.

Figure 3 shows the GDOP latitude/longitude map for a possible version of the final Starlink constellation. The caption lists the average γ and η values for this map. Averages are needed because there is a range of the semi-major axes for the orbits and because differing RE values apply to different points on the WGS-84 ellipsoid. GDOP is less than 2 everywhere on the globe. For a range-rate-equivalent Doppler-shift measurement error standard deviation of 0.01 m/sec, the achievable estimation precisions are better than 0.01×2⁄0.006=3.3 m for position, 0.01×2⁄37=0.00054 sec for clock offset, 0.01×2=0.02 m/sec for velocity, and 0.01×2⁄c=6.7×10-11 second/sec for clock offset rate.

Reference [3] plots GDOP for other constellations. A version of OneWeb suffers from poor GDOP (too large) near the equator and in mid-latitude regions if the 18 near-polar orbital planes are grouped with all of the ascending nodes on one side of the Earth and all of the descending nodes on the other side. There is poor geometric diversity of the line-of-sight rate vectors for j=1,…,N in regions where a receiver sees only south-going or north-going satellites, and GDOP suffers.

These accuracy numbers and the overall GDOP analysis have been verified through application of a batch filter to simulated Doppler shift data [3]. One simulation test has examined the impact of ephemeris errors that produce errors in the filter’s versions of the satellites’ positions, velocities, and transmitter clock frequency offsets. It considered per-axis RMS satellite position errors of 2 m, per-axis RMS satellite velocity errors of 0.002 m/sec, and RMS satellite clock offset rate errors of 3.3×10-11 seconds/sec. The resulting position error magnitudes for 100 Monte-Carlo simulation cases were 2.3 m RMS and 5.4 m peak. The velocity error magnitudes were 0.013 m/sec RMS and 0.044 m/sec peak. The clock offsets were 0.33 msec RMS and 0.90 msec peak.

The GDOP analysis and the batch filter results on simulated data both indicate absolute navigation performance similar to that of current pseudorange-based GNSS. The only significant difference is the accuracy of the estimated clock offset δR. Its precision is slightly better than 1 msec. This is at least 4 orders of magnitude worse than for pseudorange-based GNSS. The poor clock accuracy stems from the fact that clock offset is observable only because of satellite motion, not because it is tied to precise atomic clocks onboard the spacecraft.

In theory, one could use current MEO GNSS satellites to implement this navigation concept. In practice, the accuracy would be poor. The values of GDOP might be reasonably low, but the scaling parameters would be on the order of γ=2×10-4 rad/sec and η=0.2 m/sec2. A GDOP equal to 1 and a measurement error standard deviation of 0.01 m/sec would yield a position precision of 0.01×1⁄0.0002=50 m and a clock offset precision of 0.01×1⁄0.2=0.05 sec.

Advantages

There are three significant advantages to the proposed scheme. First, it might be able to operate with hardly any modifications to the planned large LEO constellations. There would be no need to fly atomic clocks aboard the spacecraft. It may be possible to exploit their downlink communication signals for navigation with little or no modification, as is done by Satelles with the Iridium downlink signals.

A second advantage is the nearness of the satellites to the users. It might enable higher received power levels that would reduce the potential impact of intentional and unintentional interference. A third advantage is the relatively inexpensive nature of the individual satellites that comprise each constellation. The replacement and upgrading of satellites could happen over a shorter average cycle, which would make the concept more adaptable.

Alternative Approaches

There are alternative ways that one might employ a large LEO constellation for navigation. One might develop a hosted payload that carried an atomic clock and a dedicated navigation signal transmitter. It could provide both pseudorange and carrier Doppler shift. In that case, standard navigation methods could be used instead of the new one proposed here.

One might use this basic concept, but have the navigation filter process accumulated delta range rather than carrier Doppler shift. In theory, such an approach should yield similar performance. In practice, it might be more difficult to use accumulated delta range as the primary observable. It may not be practical to broadcast a useable downlink signal continuously. Any attempt to reconstruct accumulated delta range would require the estimation of cycle slips during signal dead times.

Furthermore, accumulated delta range bias estimates tend to drift with time if not used in a single- or double-differenced context. The needed filtering techniques to compensate for such drift would make the system more complicated, and its performance might not exceed that of a Doppler-shift-based approach.

Some researchers have considered LEO satellite signals as a means of augmenting navigation signals from existing MEO GNSS, e.g., see [4]. This particular reference considers the ability of LEO signals to aid signal integrity analysis. Other efforts have considered the possibility of greatly reducing the initial convergence time of high precision in PPP if signals from one or more LEO satellites are available [5].

What To Do Next

There are a number of open questions about this concept. The most pressing question concerns signal availability. Although many satellites will be visible to any given receiver, their downlink signal beams (OneWeb) or their focused spot beams (Starlink) will not all be visible. It is likely that only one satellite at a time for each constellation will transmit a signal to any given point on the Earth’s surface. This is a sensible downlink communication strategy that conserves satellite transmission power and information bandwidth. Therefore, work needs to be done to figure out how to receive signals from many other satellites.

Some constellations’ FCC filings indicate that their satellites will carry omnidirectional command and control beacons. One solution to the signal availability problem would be to send periodic downlink bursts through such a beacon. Another possible technique might exploit weak signals in antenna side lobes. The main beam of a downlink signal will be very powerful in order to support high data throughputs. Therefore, it may be possible to receive such signals in side lobes, especially if small segments of them have known pseudorandom modulation patterns that can be used to achieve significant processing gains.

Another possible approach is to accept the limited signal available from any given constellation and to fuse Doppler data from multiple constellations with the help of an INS [6].

Any workable system is likely to involve a thousand or more satellites with perhaps dozens or more of their signals being received simultaneously. This presents a multiple access challenge. A practical multiple access signal modulation scheme will need to be developed.

There would be a need to distribute satellite ephemeris data and clock frequency offset data to user receivers. This information would have to be determined from some sort of ground control segment. The constellation owner could operate the segment and perhaps already is planning to do so. If the constellation owner was cooperative, then the constellation’s downlink signals could be used to disseminate this information too. Even with an uncooperative constellation owner, however, it should be possible to deduce and disseminate the needed information.

This system could probably work with short signal bursts and longer interleaved dead times. Such an approach might reduce the challenges of designing multiple access signals. Another advantage would be a large reduction in the average downlink transmission power requirement.

The one weak point of this concept is the “T” part of PNT. Receiver clock offset precision is only sub-millisecond, not sub-microsecond or better, as with current pseudorange-based GNSS. It might be possible to equip a small subset of a constellation’s satellites with atomic clocks and ranging signals. If just one such satellite were visible to each point on the surface of the Earth, then sub-microsecond timing accuracy might be achievable.

It would be good to start testing this concept or components thereof soon. One possible way to test it would be to use the Iridium constellation and to place the test receiver at a very high latitude where many Iridium satellites are visible simultaneously. The experiment would involve 8 or more simultaneously visible satellites broadcasting special L-band downlink signals that had modulations which admitted good multiple access signal processing at the receiver. Perhaps Satelles could arrange for such a test. We would like to be there if it happens, provided it is not too cold and that we have adequate clothing and protection from polar bears.

References

(1) Anon., “Satellite Time & Location Signals, 1000 Times Stronger than GPS,” Satelles, Inc., available online at: https://www.satellesinc.com/wp-content/uploads/pdf/Satelles-White-Paper-2019.pdf, 2019 (accessed 24 Oct. 2020).

(2) B. Parkinson, “Introduction and Heritage of NAVSTAR, the Global Positioning System,” in Global Positioning System: Theory and Applications, B. Parkinson and J. Spilker, Eds. Washington: AIAA, 1996, pp. 3–28.

(3) M.L. Psiaki, “Navigation using Carrier Doppler Shift from a LEO Constellation: TRANSIT on Steroids,” Proc. ION GNSS+ 2020, Virtual, Sept. 2020, pp. 3027-3045.

(4) D. Racelis, P. Pervan, and M. Joerger, “Fault-Free Integrity Analysis of Mega-Constellation-Augmented GNSS,” Proc. ION GNSS+ 2019. Miami, FL Sept. 2019, pp. 465–484.

(5) H. Ge, B. Li, M. Ge, N. Zang, L. Nie, Y. Shen, and H. Schuh, “Initial Assessment of Precise Point Positioning with LEO Enhanced Global Navigation Satellite Systems (LeGNSS),” Remote Sensing, Vol. 10, No. 984, 2018, pp. 1-16.

(6) B. McLemore and M.L. Psiaki, “Navigation Using Doppler Shift from LEO Constellations and INS Data,” Proc. ION GNSS+ 2020, Virtual, Sept. 22-25, 2020, pp. 3071 – 3086.

Authors

Mark L. Psiaki, is professor and Kevin T. Crofton Faculty Chair of Aerospace and Ocean Engineering at Virginia Tech, and professor emeritus of mechanical and aerospace engineering at Cornell University. He holds a Ph.D. in mechanical and aerospace engineering from Princeton University.

Brian McLemore is a Ph.D. student of aerospace engineering at Virginia Tech. His research interests include GNSS digital signal processing and estimation and filtering.