Link-Layer Coding: A Way to Speed-Up Nex-Gen GNSS

The time-to-first-fix (TTFF) is the time that a GNSS receiver takes to make available for the first time from switch-on an indication of the user position. Smaller TTFFs have become a premium performance metrics for any receiver, particularly as smartphones, tablets and location-based services have expanded so rapidly.

The TTFF depends on a number of factors, some specific to receiver design, others depending on the particular conditions the receiver operates in (urban canyon, indoors, foliage, etc.). Still others depend on GNSS system design. Concentrating on the last factor, when GNSS is the only means to obtain user position, reliable and fast decoding of the navigation data message is mandatory. Robustification of the navigation message is usually achieved through coding/interleaving solutions at the physical layer, but the particularly harsh environments just mentioned may require more.

All operational GNSSs organize the diverse messages in a hierarchical structure and broadcast them in a carousel fashion, repeatedly transmitting the same navigation message a certain number of times before updating. The navigation message is divided into frames, which in turn may be further divided into sub-frames and so on. Here we refer to a page as the smallest unit of the navigation message handed to the Navigation Signal Generation Unit (NSGU) aboard the satellite. Each page, before being coded with a Forward Error Correction (FEC) (or channel) code, is supplemented with a further Cyclic Redundancy Check (CRC) whose aim is to allow the receiver to check on the integrity of the coded page.

When a page passes the CRC in the receiver, it is immediately handed over to the link layer (the upper layer of digital processing in the receiver) for further processing. When the CRC fails, the page is affected by errors, and consequently it is discarded. In the latter case, the receiver must wait for the next re-transmissions of the message in the carousel to be able to retrieve the lost pages. In harsh environments, the fraction of lost pages is not negligible. This may considerably increase the time necessary for the receiver to recover all the message pages from the start of reception and may ultimately strongly affect the TTFF.

To better protect the integrity of pages in adverse conditions, we propose the use of a relatively novel technology, link-layer coding (LLC). Its rationale is that the diverse pages are processed at the link layer by the formatter of the navigation message before being delivered to the NSGU. This encoding is not just the carousel repetition found in GNSSs today; it is a smarter encoding strategy that takes place at the link layer.

Channel- and Link-Layer Coding

Channel codes, a.k.a. FEC codes, is a technique to protect digital data against noise, distortion, and interference perturbing the GNSS signal. Such technology, commonplace in wireless communications from the ’70s, is one of the flagship technologies of modern Galileo and modernized GPS, as opposed to legacy GPS. To make it as simple as possible, if we want a block of K information bits of a navigation message to be more robust, we can just append a number of additional redundant bits, the so-called parity-check bits, derived through modulo-2 additions of subsets of our original K ones, thus obtaining a length-N codeword (N > K), which will aid the receiver locating and correcting possible errors that are caused by transmission noise. The above description refers to a systematic code, where the source bits appear unchanged in the codeword. The resulting coding rate, i.e., the ratio between the number of information bits before encoding to the number of coded bits afterwards, is rc = K/N.

In actual systems like Galileo or modernized GPS, the channel codes used at physical layer are sophisticated examples of channel codes. As physical-layer code, Galileo uses a convolutional code with Viterbi decoding, and modernized GPS uses Low-Density Parity Check (LDPC) codes. The latter will be a fundamental component of our novel idea of LLC codes that we will describe later on.

In some cases, the parity-check bits can only be used to detect the presence of errors in the received codeword, without doing anything to correct them. This is precisely the case of the CRC that is appended to each message page of any GNSS. If some error is detected, then the page that is affected by that error is just discarded or erased, and it is not used by the receiver.

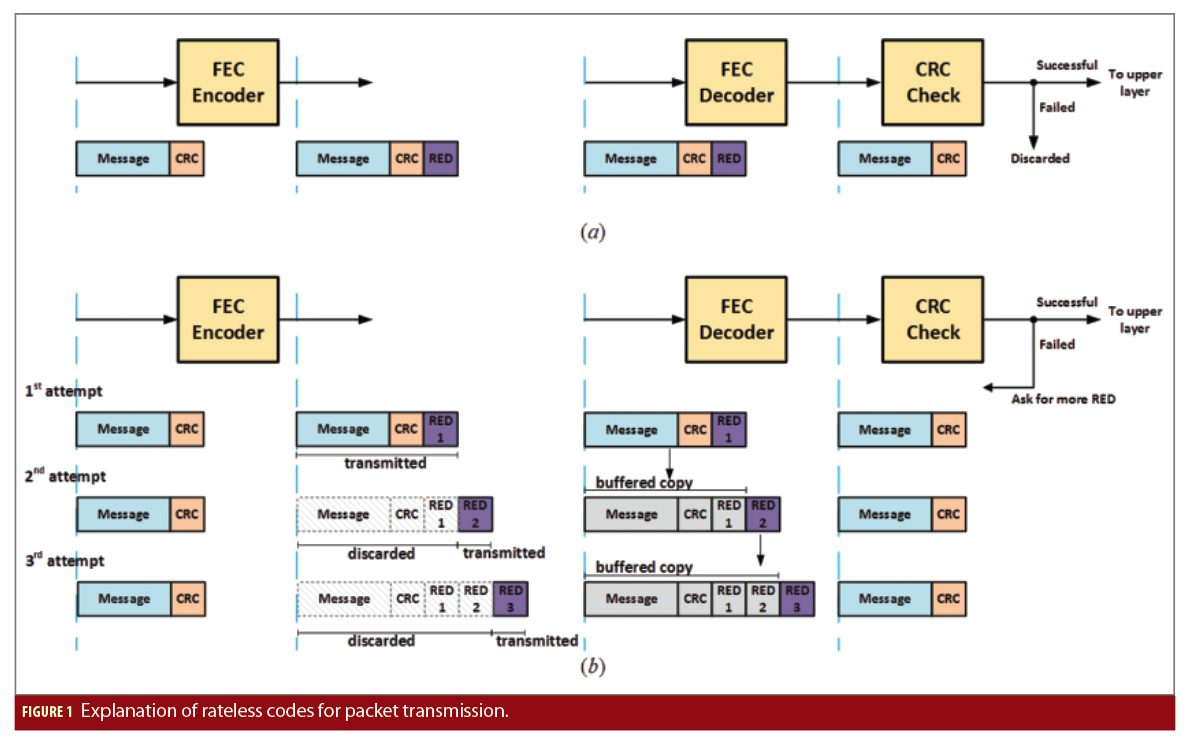
Let us now come to LLC and rateless codes. Let us refer to conventional packet data communications and assume for the moment that a low-capacity feedback channel is available between the receiver and the transmitter. After CRC insertion and physical-layer encoding, the overall format of a packet is shown in Figure 1(a), left. In spite of the capability of the channel code, it may happen that some residual errors are present on the packet after channel decoding, so that the CRC in the receiver fails and the packet is erased. The usual remedy to this situation is a request by the receiver, sent back on the feedback channel to the transmitter, to send out the packet again.

The idea of rateless codes is the following: instead of retransmitting the whole packet, with a waste of capacity and time, the transmitter just sends out more redundancy bits, in the hope that they will allow removal of all residual channel errors and grant successful recovery of the packet. Several rounds of transmissions of additional redundancy bits can take place, until the packet is recovered. The final rate of the code is therefore not known in advance, and this is why this kind of coding is called rateless. Rateless coding is more efficient (albeit more complicated for the receiver) than simple retransmission request.

What if no feedback channel is available, as in broadcasting and in GNSS? We can imagine an endless source of parity bits, a “fountain” of redundancy to tame the thirst for clean bits of the receiver, the ultimate form of rateless encoding (Figure 1(b)). In such a theoretical approach, called fountain coding, the receiver tries to decode the packet as soon as it receives a few parity bits; if the attempt is not successful, it goes on with further parity bits until all errors are removed. With fountain coding, there is no retransmission request since every receiver will get out of the fountain the amount of redundancy it needs. Of course, the fountain is not endless in the practice, there is always a limit on the amount of water (i.e., of parity bits) that is spilled out.

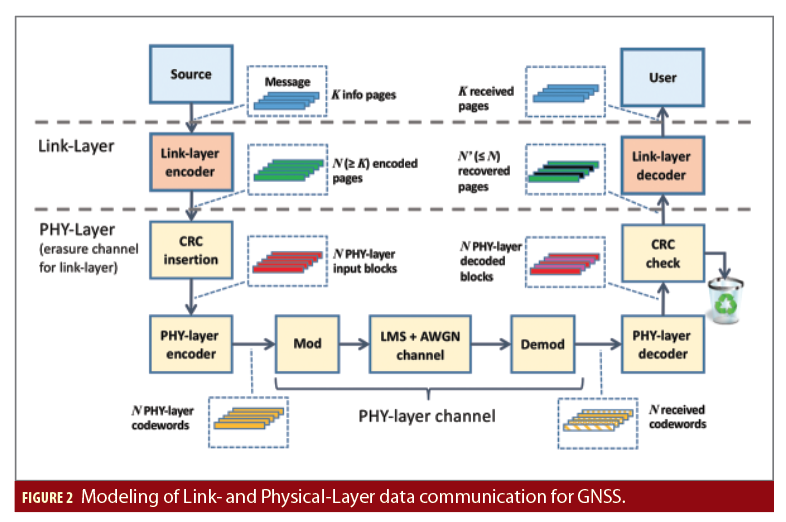
Fountain codes are the basis of standard LLC that we propose to apply to GNSS. The overall appearance of the resulting data-link model that encompasses both the physical and the data-link layer is depicted in Figure 2. As is seen, the digital message to be transmitted (our overall navigation message) is composed of K equal-sized information pages. Each page is first processed by the link-layer encoder (whose operation and scope we will discuss in a moment), which adds a first layer of redundancy and produces N ≥ K link-layer coded pages. The coded pages undergo insertion of the CRC, physical-layer encoding, modulation (which may include spectrum spreading) and, eventually, radio transmission on a Land-Mobile Satellite (LMS) channel. After radio propagation, the radio signal is synchronized and demodulated in the receiver, then the digital message is decoded and CRC-checked. If the check is successful, the corresponding page is correctly retrieved and handed over to the link-layer decoder, otherwise it is erased. For this reason, the link layer sees a so-called Page Erasure Channel (PEC), in that each page in the message is either correctly received or entirely discarded.

In current GNSSs, the K pages composing the navigation message are transmitted in carousel fashion a predefined number of times ρ before being updated. For example, the Galileo I/NAV message for the almanac is composed of K = 48 pages by 2 seconds each, organized in 2 pages per sub-frame, with a carousel transmission consisting of 24 sub-frames (transmitted in a total of 720 seconds). Instead, for GPS L1 C/A, the same message is composed of K = 50 pages (almanac and other constellation information), transmitted in 2 pages per frame, with a carousel consisting of 25 frames.

LLC Application to Next-Gen GNSS

We now examine properties of the navigation message that make it intrinsically amenable to the application of LLC, but that also require some caution when designing such codes:

• The LLC coding rate can be very low, and even become vanishingly small, since the navigation message (e.g., almanac) may not change over several days (think of simple carouseling).

• Reception is asynchronous, i.e., the receiver starts receiving at any time without specific reference to the start of the message (carousel).

• Certain types of messages are transmitted by multiple satellites, so that the LLC scheme becomes an instance of network coding (extension of transmission diversity).

• The message size K (in pages) is typically small-to-medium, ranging from a few tens to a few hundreds. This fact advocates caution when designing an LLC scheme based on the typical design rules, which are often conceived on the contrary for large block lengths and therefore make use of asymptotic properties that may not hold here.

• Unlike many applications, in which the block erasure probability is the performance parameter of interest, the main figure of merit for GNSSs is the time-to-retrieval (TTR), i.e., the time that the receiver takes to retrieve the message part under consideration, so that the typical design rules for LLC must be revised in order to keep into account this shift in the perspective.

In our research geared towards the design of new-generation GNSSs, we specifically focus on three different LLC schemes whose performance will be assessed in:

• Trivial carousel transmission;

• Low-rate fountain code (the current state-of-the-art of LLC) without any carousel transmission;

• Short-block rate-rc code cascaded with (low-rate) carousel transmission–our novel solution wherein the short-block code is an LDPC not on bits, but on pages.

FOUNTAIN CODES. Fountain (or rateless) codes were originally designed to allow efficient and asynchronous broadcast in wireless communication networks. In general, a fountain encoder is an algorithm that, given a size-K binary information block, produces a potentially endless stream of encoded symbols c0, c1, …, where each ci is a linear parity-check bit, whose check equation has randomly chosen coefficients (i.e, the parity bit is the XOR of a random subset of the information bits). Moreover, different checks are chosen independently of each other, according to a predetermined probability distribution. The most important classes of Fountain codes are Luby-Transform (LT) codes and Raptor codes.

For LT codes, the parity checks are derived in the following way:

• The degree of the linear check (i.e., the number of bits to be XORed), ranging from 1 to K, is randomly drawn according to a certain optimum probability distribution Ω. Call d the resulting degree for a certain parity check.

• The set of d input (information) symbols that contribute to the check (i.e., those that are to be XORed) are chosen uniformly at random in the input block.

As is apparent, a given LT encoder is characterized by the two parameters (K, Ω). For a given value of K, a good choice of Ω is the so-called robust soliton distribution. Using such probability distribution in the definition of the check equations, we are guaranteed that the LT decoder will successfully decode any codeblock with probability 1−δ as soon as K+ 2s log(s/δ) encoded symbols are received, where s is a design parameter. The pattern of random extractions used by the encoder to generate the parity symbols has to be known by the decoder too, so that checks are actually performed according to a pseudo-random number generator whose initial seed is agreed between encoder and decoder.

Because of near-optimal performance, Raptor codes have become the state-of-the-art Fountain coding technique. A Raptor encoder can be described as the serial concatenation of an outer, “classical” (i.e., fixed-rate) FEC encoder and an inner LT encoder as above. The introduction of the precoder avoids the real bottleneck in the performance of an LT code. Indeed, LT-encoded message symbols become progressively more and more difficult to recover, requiring more and more check symbols to be received. If we cascade an outer code with the LT code, we do not actually need to LT-decode all the message symbols, since the outer decoder will anyway fix the remaining erasures thanks to the (small) added redundancy.

The systematic Raptor code for multimedia broadcast and multicast services (MBMS) over 3G cellular networks was designed to be simple and to work well for relatively short blocks, ranging between 500 and 8196, so it is worth of consideration. In that scheme, precoding is organized in two phases: the first stage makes use of a regular systematic LDPC code that adds S parity check symbols to the original K input symbols. The second stage is somewhat similar to a Hamming code and provides further H symbols. The precoder output is therefore composed by N=K+S+H intermediate symbols and undergoes LT encoding.

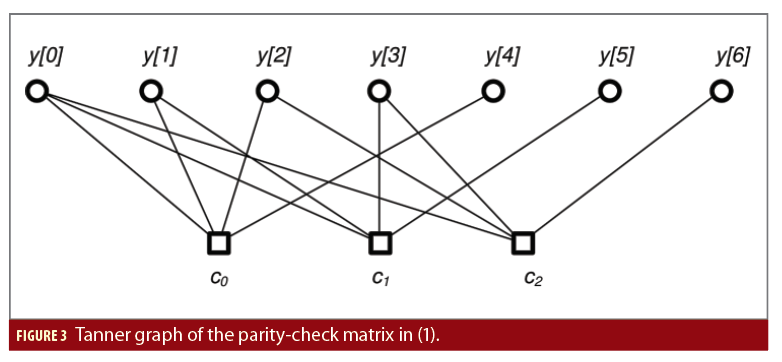
LOW-DENSITY PARITY-CHECK CODES. LDPC codes are conceptually very simple and belong to the vast class of parity-check codes. Like any such code in fact, an (N, K), rate rc = K/N binary LDPC code is characterized by its (N−K)×N binary parity-check matrix H, the only peculiarity being that such matrix is sparse or low-density, i.e., it has a very small number of “ones”. The code may be also characterized by its Tanner graph, which is the bipartite graph whose incidence matrix is H. Specifically, the Tanner graph is composed by N variable nodes (VNs), each of which corresponds to a different column of H, and by N−K check nodes (CNs), corresponding to the rows of H. The graph has got an edge connecting the j-th VN and the i-th CN if and only if the (i, j) element of H is 1. For example, if our parity-check matrix is

then its corresponding Tanner Graph is shown in Figure 3.

When the LDPC code is used on the erasure channel, the decoder input is a received codeword y with length N, wherein some of the (coded) symbols are erased, while the non-erased symbols are received correctly. To decode an LDPC code on the erasure channel, we have essentially two options: either message-passing (MP) or maximum-likelihood (ML) decoding.

The MP decoder works on the abovementioned Tanner graph of the code as follows. Each received symbol is assigned to the corresponding VN in the graph. Then, the CNs that are connected to a single erased VN can be immediately used to recover the value of such VN: the checksum of the node has in fact to be equal to zero, and so the erased value can be reconstructed. If the recovered VN was connected to another CN with two erasures, then we can un-erase another symbol, and so on in an iterative fashion. This VN recovery is repeatedly performed in several iterations until the MP decoder stops, either when there are no erasures left (and in this case decoding is successful), or when all CNs that are connected to remaining erasures are connected to at least two of them. In the latter case, the decoder gets stuck and decoding is not successful.

The ML decoder is optimal in the sense that it minimizes the probability of decoding failure, and for the erasure channel boils down to solving a linear system, which entails an increase of computational complexity with respect to the MP decoder. A suitable trade-off between performance and complexity is the hybrid MP/ML decoder. The idea is very simple: after receiving the channel output, low-complexity MP decoding is performed first. If decoding is not successful, which means that some erased VNs were not recovered, an ML decoder is further applied to try and recover such residual erasures. While the performance of the hybrid decoder is the same as that of ML decoding, its complexity is in between that of the (simple) MP decoder and that of the (complex) ML one.

In our application of LLC to our case of reference (Galileo I/NAV), variable nodes correspond to message pages. An ad-hoc design has been devised to obtain LDPC codes with good TTR performance. The design procedure consists in standard LDPC code design for erasure probability minimization, cascaded with an optimal code permutation search, which produces
close-to-optimal TTR performance.

What Can We Gain from LLC?

We present now some performance results of the described LLC schemes, evaluated by simulation on a synthetic Land-Mobile Satellite (LMS) channel. Our main performance metrics will be the average TTR as a function of the line-of-sight (LOS) signal-to-noise ratio (SNR) C/N0, in dBHz, of the LMS channel, i.e., the value of the SNR we would get in the same propagation conditions but in the absence of the LMS channel attenuation due to shadowing and fading.

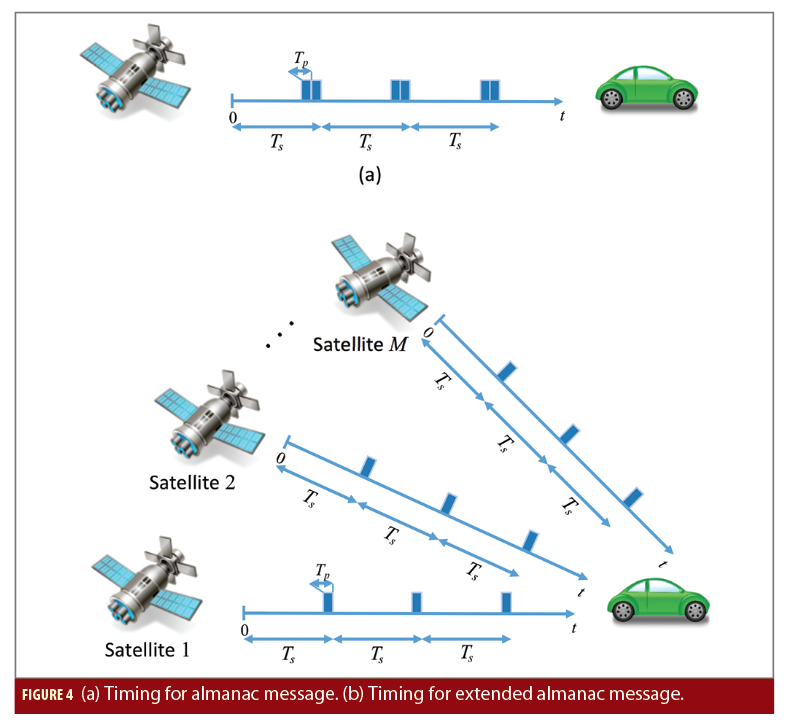
Our first result is simple: there is very little to gain by the application of LLC to short messages like CED data. We state this without the need to support it with any quantitative data since it is quite intuitive. On the contrary, we found considerable gain for two different types of long messages: the first one is just the current Galileo I/NAV almanac, composed as we already mentioned by K=48 pages, and assuming single-satellite reception. In each subframe of duration TS=30 s, there are two consecutive pages (of duration TP=2 s) carrying the almanac message, as shown in Figure 4(a).

The second message format is a hypothetical extended almanac made of K=192 pages to be disseminated through Galileo I/NAV, assuming multi-satellite dissemination from M satellites (as is the case today for the almanac). We suppose that in each 30-s subframe, there is a single transmitted 2-s page, and that all satellites are synchronized, as shown in Figure 4(b). For carousel-based schemes, we impose suitable offsets on the carousel starts for each satellite in order to optimize the TTR.

The set-up of the simulations is the following: the physical-layer code is the Galileo I/NAV con- volutional code, with optimal Viterbi decoding. Perfect synchronization and LMS channel estimation is assumed. The received LOS C/N0 takes also into account an elevation-dependent antenna gain. The different options in terms of LLC are:

• Legacy carousel;

• Ideal LLC, i.e., a scheme able to recover the message as soon as any K encoded pages are correctly received;

• LT code with robust soliton distribution and s ≈ K;

• MBMS standard Raptor codes;

• Two different rate-1/2 LDPC codes of lengths N=96 and N=384, respectively, cascaded with carouseling.

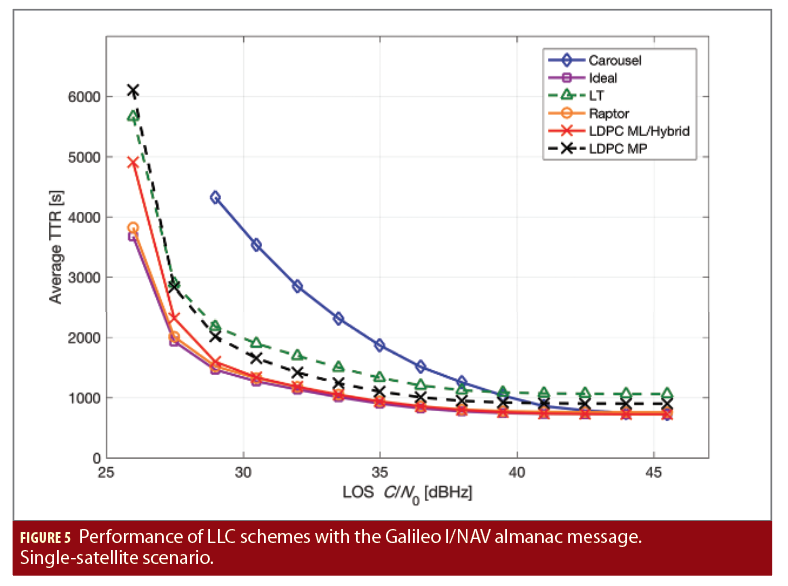
Figure 5 shows the average TTR for the different LLC techniques in the case of the almanac message. The LMS time series was obtained by simulating a model for an elevation of 25°, an urban environment, and a user speed of 5 km/h. The sampling time is about 97 Hz, while the time series duration is equal to 30 hours. The solid lines refer to LLC schemes with ML/hybrid decoding, while the dashed lines refer to LLC schemes with MP decoding.

The Raptor code has a performance very close to ideal (4–5% degradation), and substantially outperforms the carousel scheme for C/N0 lower than 40 dBHz. On the contrary, the average TTR curve for the LT code incurs a penalty of about 45–50% with respect to the optimal performance. The LT code suffers from the lack of precoding and the use of an MP decoder, which is definitely sub-optimal with short blocklengths compared to the ML decoder of the Raptor code. Our novel rate-1/2 LDPC code (with the ML/hybrid decoder) exhibits a very good performance above 30 dBHz, with a sizable degradation below. The black dashed curve depicts the performance for the LDPC Code with MP decoding. The corresponding TTR is larger by about 15–25% with respect to the hybrid/ML decoder.

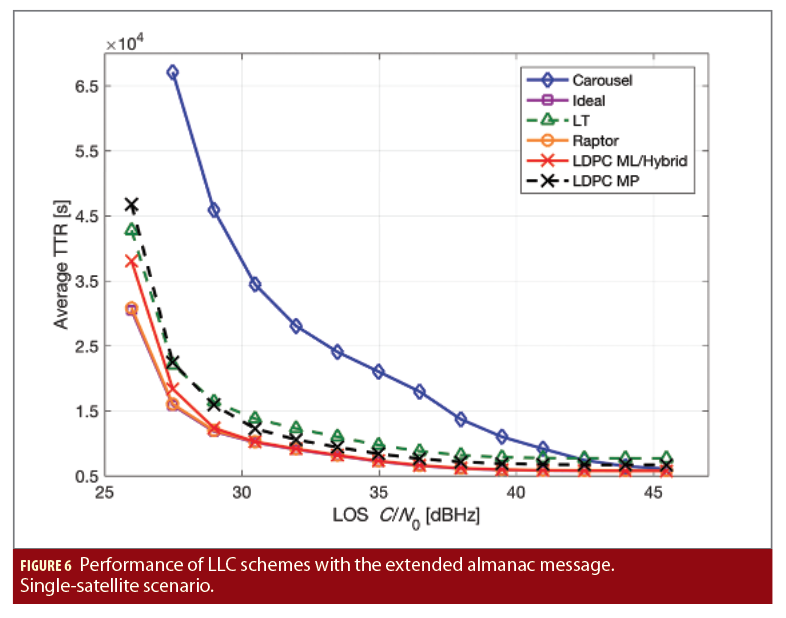
The same kind of performance is shown in Figure 6 in the case of the Galileo I/NAV extended almanac and for the same scenario. The hierarchy between the curves is the same as in the previous case, but the differences are enhanced, because of the larger message length.

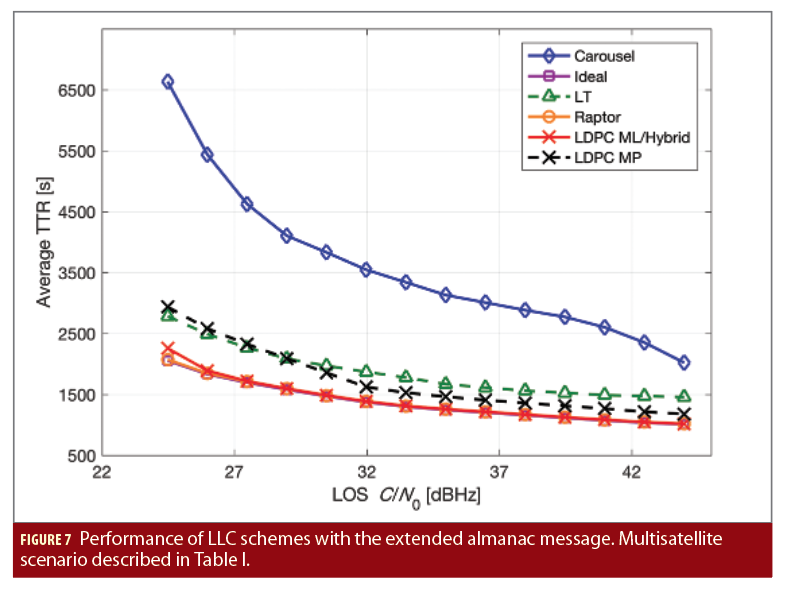
We then move to a multisatellite scenario. In particular, we considered the well-known 2-state semi-Markov model for the LMS channel, and create a multisatellite time-varying constellation with the parameters defined in Table 1. Within a 3-hour simulation time, the 6-satellite constellation takes six different elevation-azimuth combinations, each lasting for half an hour. In Figure 7, we show the average TTR for the extended almanac. Again, the Raptor code is a very good approximation of ideal LLC, while the LT code has a fixed penalty, for all C/N0 values. Regarding the carousel-based schemes, our novel rate-1/2 LDPC code, when ML decoding is employed, largely outperforms the carousel, and has close-to-optimal performance above 27 dBHz.

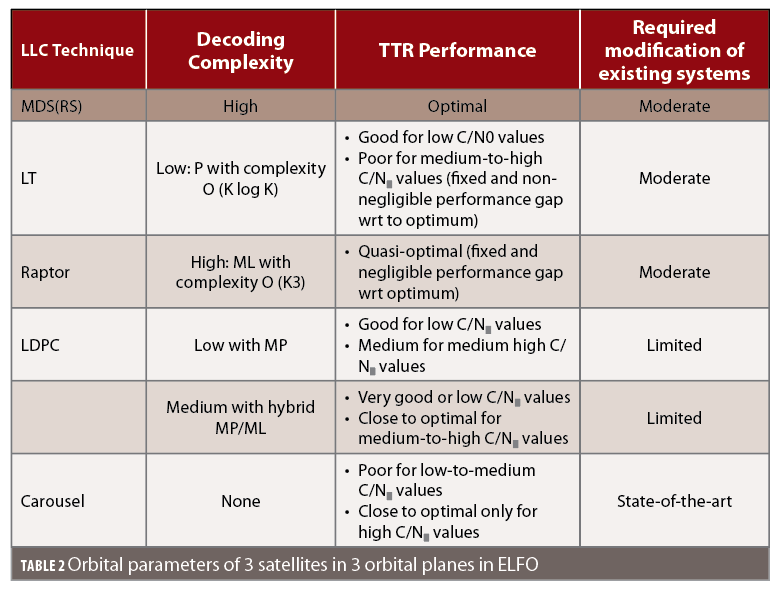
To summarize, Table 2 shows a comparison of several LLC techniques under different points of view. The first row refers to maximum-distance separable (MDS) codes, a class of which Reed-Solomon (RS) codes are a subclass. These codes are characterized by ideal performance, but also by a rather large decoding complexity, since they are nonbinary codes with algebraic decoding.

As a final performance evaluation, we show some semi-analytic results obtained after a theoretical analysis of LLC paired with simulation of the LMS channel. The theoretical model needs to know the values of the page erasure rate (PER) for the different sections of the message. From this input, it derives the average TTR of the receiver. In our evaluation, the PER values were obtained from the detailed simulation of a physical-layer LMS channel applied to the GALILEO I/NAV message, then we exported the resulting statistics in term of PER to our theoretical link-layer model. We call this abstraction.

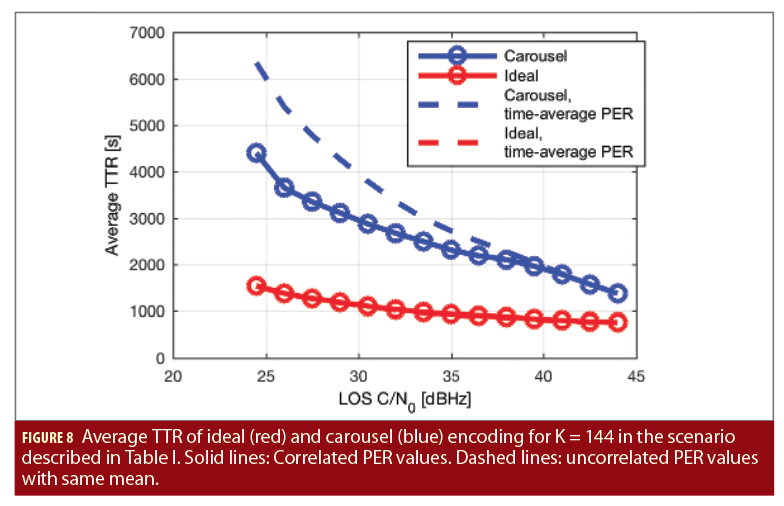
The PER vector p is obtained by decoding the received physical-layer codewords of Galileo I/NAV with an optimal Viterbi decoder, for the 64-state, rate-1/2 convolutional code. The input length of the physical-layer code is equal to 120 information bits and TP = 2 s. The message size is equal to K = 144 pages. The arrival time of the i-th coded page, i = 0, 1, …, is given by

where ∆ = 30 s, which means that, for a given satellite, pages are equi-spaced and that the different satellites are synchronized. Finally, the reception start time is uniformly distributed over the whole simulation time window (with the PER vector wrapped around whenever there is need for a transmission tail).

Figure 8 shows the simulation results in terms of average TTR as a function of LOS C/N0, in the same 6-satellite scenario of Table 1. Carousel encoding results in a TTR that is two to three times the TTR for ideal encoding. We also plotted (dashed curves) the analytic expression of the TTR when the actual, time-varying PER vector is replaced by its corresponding time-average over the entire simulation. While for ideal encoding this results in a negligible error, the difference for carousel encoding is large for low C/N0 values only. In particular, approximating the PER vector with its long-term mean results in an overestimate of the actual TTR performance. A heuristic way of explaining the fact that carousel encoding seems to take advantage of the channel memory, at least in the considered scenario, is the following. Erasures happen in bursts, as well as successful receptions. If in both cases the average burst length is equal to B, we can roughly say that the channel looks like a memory-less channel for a message with length K/B. This effective reduction in the carousel length proves beneficial when the average PER is large enough.

Summary, Conclusions and Perspectives

We have shown how to effectively apply the well-known notion of link-layer coding to the specific issue of the protection of GNSS navigation messages. Considering as our reference study case the Galileo I/NAV message, we have shown that the use of simple link-layer codes provides considerable reduction in the time that the GNSS receiver needs to correctly receive and decode the navigation message, with respect to the case of current plain carousel transmission. We have also shown that the performance of simple and practical LLC schemes, like our novel ad hoc page-level LDPC code, is very close to that of an ideal LLC performance. The performance improvement is really considerable in all of those impaired situations (urban canyon, indoor reception, strong shadowing by trees) wherein current decoding times are really prohibitive, especially for long messages such as almanac and extended almanac data.

In addition, the adoption of such technology can have minimum impact or can even be totally transparent to the space segment of current GNSSs—they could be upgraded by a simple redefinition of the navigation message structure. Concerning user receivers, new chipsets would need the addition of the LLC decoder to be able to actually exploit the benefits of the new technology. A partial exploitation of LLC encoded messages could be obtained with the use of systematic codes, for which part of the codeword coincides with the uncoded message. In such a case, a receiver without link-layer decoder could retrieve the message, provided that it knows where the systematic pages are located within the transmission frame.

In conclusion, more work will be needed to test and validate different coding schemes in different scenarios, as well as to exploit practical implementations of it. Nonetheless, we believe that future generations of GNSSs (and possibly, modernization of current ones) will greatly benefit from the adoption of this technology.

Acknowledgment

This research was developed within the framework of ESA-funded projects ADVISE and GNSS end-to-end. The content of the present article is research reflecting solely the authors’ view and by no means represents the official ESA view or the one from Galileo or EGNOS Project Offices.

Authors

Alberto Tarable received his Ph.D. degree from Politecnico di Torino. He holds a research position at the Institute of Electronics, Information Engineering and Telecommunications (IEIIT) within Italy’s National Research Council. His main research topics have encompassed most aspects of the physical- and MAC-layer design of communications, such as channel coding, MIMO systems, phase-noise channels, multiuser receivers.

Riccardo Andreotti received a Ph.D. in information engineering jointly from the University of and the Université Catholique de Louvain, Belgium. He currently works with with MBI in the research and development team on topics related to the air-interface of satellite communication systems.

Marco Luise is a professor of telecommunications at the University of Pisa. He is the co-founder of the International Journal of Navigation and Observation and an IEEE Fellow. His main research interests lie in the broad area of wireless/satellite communications and positioning.

Francesca Zanier received her Ph.D. from the University of Pisa, Italy. She is currently a radionavigation system engineer at the European Space Agency, ESTEC. Her primary areas of interest include signal processing, estimation theory, GNSS receivers, and signals and navigation applications.

Stefano Cioni received his Dr.-Ing. degree in telecommunication engineering and Ph.D. from the University of Bologna respectively. He is currently a telecommunication systems engineer at the European Space Agency within the Radio Frequency Systems, Payload and Technology Division. He is a senior member of the IEEE Society.