Q: How do you use GNSS to compute the attitude of an object?
A: GNSS technology is used to support a wide range of position, velocity and time applications across numerous platforms. One of the lesser-known applications of GNSS is its ability to determine the attitude, or orientation, of an object. Such systems can be made to be quite small and can yield accurate solutions that operate in virtually any environment in which GNSS satellite visibility is reasonable. The only requirement from a GNSS receiver perspective is that the receiver be able to provide reliable carrier phase measurements.
This article begins with a brief summary of how the attitude of a vehicle is determined and then explains how GNSS can be used. It wraps up with a brief discussion about attainable accuracies.
Attitude Determination
Attitude determination is the process of determining the rotation angles that relate two different coordinate frames. Although any two coordinate frames can be used, we herein consider the rotation between a local-level frame (e.g., North, East, Up or East, North, Down, etc.) and the body frame. The body frame is a frame attached to the object (“body”) whose attitude is desired (an example body frame is given later).
With this in mind, we present the following key relationship
r⃗l = Rlbr⃗b (1)
where r⃗ is a vector parameterized in the local-level (superscript l) or body (superscript b) frame and Rlb is the rotation matrix (or direction cosine matrix) from the body frame to the local-level frame.
The rotation matrix between any two frames can be defined using three consecutive rotations about the three coordinates axes — these are called Euler angles. For the case under consideration, since one of the frames is the local-level frame, the Euler angles can be expressed as familiar roll, pitch and azimuth angles.
To compute the rotation matrix, one needs to know or measure at least two vectors in each coordinate frame. These vectors could be anything including velocity, rotation rates, etc., as long as they are non-collinear (i.e., not parallel). It is possible to use a single vector, but then you cannot determine all three Euler angles; more on this later.
GNSS Attitude System Setup
For GNSS attitude determination systems, the vectors used in equation (1) are relative position vectors. The question, of course, is: where do these come from?
Before answering this question, let’s clarify what constitutes a GNSS attitude system. To determine the full attitude, at least three GNSS receivers are needed. The only other requirement is some software to process the data from these receivers.
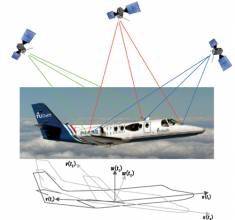
Returning to the question that opened this section, the body frame vectors are defined by the location of the receivers (actually the antennas; denoted A ‒ C) on the object whose attitude is desired. Assuming a three-antenna system, a common (if not easy to understand) configuration is to mount the antennas such that two antennas fall along the direction of travel, and the third one is 90 degrees offset. One possible setup is illustrated in Figure 1 (see inset photo, above right) for the case of a road vehicle.
Once installed, the body frame coordinates are defined by measuring the position of the antennas relative to the coordinate frame of the vehicle. The coordinate frame of the vehicle can be arbitrarily defined but is usually selected such that one axis is along the direction of travel, one lateral to the direction of travel, and the third axis completes on orthogonal frame (e.g., forward, right, down).
As might be expected, these same vectors in the local-level frame are determined from GNSS measurements. Once computed, the rotation matrix between the body and local-level frames can then be determined. Both of these steps are accomplished by the processing software and are discussed in the next section.
Data Processing
As mentioned, the inter-antenna vectors in the local-level frame are computed from GNSS. For an N-antenna system, only N-1 independent vectors need to be solved. Although not required, this is commonly done by selecting one antenna/receiver as the “base” and then computing the vector to each of the other antennas/receivers in the system.
Continuing with the three-receiver example in Figure 1, we select antenna A as the base and compute vectors ray AB and ray BC. Of course, if there are other antennas, the vector from Point A to each point would also be computed.
To be more specific, the inter-receiver vectors are computed using standard differential carrier phase processing. Because the inter-antenna spacing is typically limited to a few meters, the spatially-correlated orbit, ionosphere and troposphere errors are virtually zero. This dramatically simplifies the ambiguity resolution process, since the only errors that need to be handled are multipath, noise and antenna phase center variation, which are generally small, as discussed later.
It is also possible to use the known baseline length between the receivers (as measured in the body frame), or any a priori attitude information to make the ambiguity resolution process even more robust.
Some of you might be wondering why I have not mentioned the requirement for a base station. The reason is precisely because we are estimating relative, not absolute, position vectors. By definition, differential data processing yields a relative position vector. If the location of the base station is known in an absolute sense — this is the most common use of a base station — then the resulting solution of the rover is also absolute.
For attitude determination, absolute location is not important. As such, the location of the base receiver (Point A in the above example) can be computed from a standalone (single point) solution. Even absolute positioning errors of 100 meters (which would be extremely large if the carrier phase data needed for attitude determination is still available) will be buried by the other errors in the system, and thus can be ignored.
The only other effect that might be important here is the timing accuracy of each receiver. As discussed in the March/April 2011 GNSS Solutions column, “GNSS Receiver Clocks,” a relative timing error of Δt between the receivers will result in a relative position error of s · Δt, where s is the speed of the vehicle. Assuming a timing error of 2 milliseconds (most receivers limit timing errors to ±1 milliseconds) and a vehicle traveling at 100 kilometers per hour, the relative positioning error would be approximately 5.6 centimeters. As discussed below, this would dominate the error budget and would therefore have to be properly accounted for.
The outputs of the GNSS processing are the vectors in the local-level frame; these can be computed directly in that frame or can be computed from vectors in an Earth-Centered Earth-Fixed (ECEF) frame. Mathematically, this is written as
r⃗GNSS = r⃗l + n⃗GNSS
= Rlbr⃗b + n⃗GNSS (2)
where r⃗GNSS is the GNSS-derived vector in the local-level frame, n⃗GNSS is the measurement noise, and equation (1) was used to get from the first to second line. Equation (2) is written in parametric form and can thus be used as input to any standard least-squares or Kalman filtering estimation algorithm to estimate the Euler angles embedded in Rlb.
Two-Antenna Systems
Until now, we have only considered systems consisting of three or more receivers in order to estimate the full attitude of an object. However, two-receiver systems can be used to estimate rotations orthogonal to the vector connecting the two antennas.
The most common two-receiver system is one where the two receivers are set up parallel (or orthogonal) to the direction of travel. This allows for estimation of the azimuth and pitch (or roll) of the vehicle; the third angle is unobservable.
Expected Accuracy
As discussed above, the GNSS measurement errors are limited to multipath (2‒3 centimeters), noise (less than 1 millimeter) and phase center variation (1‒2 centimeters or less) (all values quoted as one standard deviation values). Assuming the measurement geometry is reasonable (HDOP ≈ 1 and VDOP ≈ 1.5), the main factor affecting accuracy is the length of the inter-antenna vectors.
To illustrate, let’s consider a two-receiver system with the understanding that there is an analogous relationship for three-plus receiver systems. Specifically, for the setup in Figure 2 (see inset photo, above right), for an inter-receiver separation of d, the pitch (ϕ) and azimuth (α) can be computed as
(see inset photo, above right for equations)
where σEIN is the North/East relative positioning uncertainty, σU is the vertical relative positioning accuracy, and dh is the horizontal distance between the receivers. In other words, the longer the inter-receiver separation the better the attitude accuracy.
To give some numbers, for the lower- end measurement errors and DOP values listed at the start of this section, and nominal horizontal receiver separation of 1 meter, the pitch and azimuth accuracy would be 1.3 and 1.9 degrees, respectively. This is a one-off accuracy estimate and further filtering/ averaging would yield even better performance.
Summary
This article has given an overview of how GNSS can be used to determine the attitude of an object. Although reliant on ambiguity resolution, the short baselines involved make the process quite robust. The result can be highly accurate attitude estimates that can be applied to a wide range of applications.