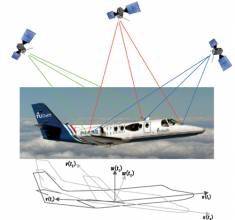
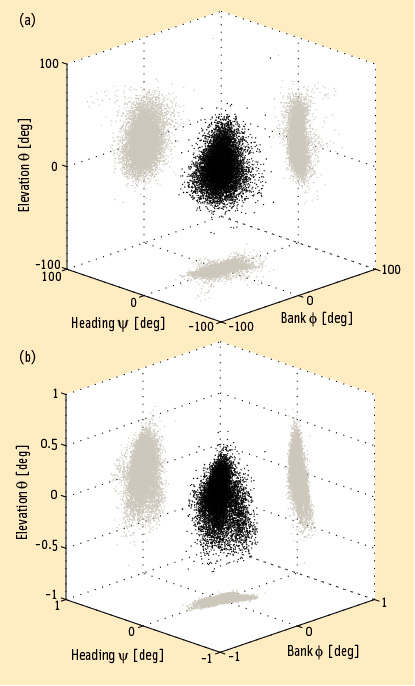
 FIGURE 1: Heading, bank and elevation angles of an actual platform carrying two perpendicular two meter-long baselines. The attitude solutions are shown for both the derived, or float, measurements (top), as well as the carrier phase-based, or fixed, measurements obtained after having correctly resolved the integer ambiguities (bottom). Precision differs between the methods by two orders of magnitude. Gray dots represent the two-dimensional projections on each of the three coordinate planes.
FIGURE 1: Heading, bank and elevation angles of an actual platform carrying two perpendicular two meter-long baselines. The attitude solutions are shown for both the derived, or float, measurements (top), as well as the carrier phase-based, or fixed, measurements obtained after having correctly resolved the integer ambiguities (bottom). Precision differs between the methods by two orders of magnitude. Gray dots represent the two-dimensional projections on each of the three coordinate planes.Working Papers explore the technical and scientific themes that underpin GNSS programs and applications. This regular column is coordinated by Prof. Dr.-Ing. Günter Hein, head of Europe’s Galileo Operations and Evolution.
Two or more GNSS antennas mounted on one platform may be used as a viable attitude-sensing tool. Although less precise than other sensors, GNSS-based attitude determination is relatively inexpensive and, most importantly, drift-free, unlike inertial sensors.
The orientation of a body with respect to a given reference frame can be estimated by employing two or more antennas. Precise baseline estimates are made available by processing incoming GNSS signals. These can be directly translated into angular estimations of attitude, the accuracy of which depends primarily on two factors: GNSS observation quality and the length of baselines between antennas on a platform.
Often one has no control over the latter, because the size and geometry of the platform limit the maximum distance at which the antennas can be placed. Thus, the challenge of obtaining precise angular estimates relies on observation accuracy.
Although GNSS code observations may be used to derive an attitude solution, we generally prefer not to rely solely on these measurements, because for most applications code-based accuracy is inadequate. Alternatively, carrier phase–based position solutions are two orders of magnitude more accurate; however, exploiting carrier phase observations is not a trivial problem.
Only the fractional part of the incoming GNSS phase signal can be detected, making the phase ambiguous by an integer number of full cycles. Correct integer values must be determined by resolving these ambiguities in order to use the carrier phase observations in the attitude estimation process.
Figure 1 (see inset, above right) illustrates the large difference that occurs between code-based, or float, and carrier phase-based, or fixed, attitude solutions using a two-meter static baseline. Only the fixed phase-based solution is capable of sub-degree accurate angular estimations, an improvement of two orders of magnitude compared to the float solution.
Given a matrix of baseline coordinates B and a matrix of local baseline coordinates F relative to the platform, estimating the platform attitude is found using the orthonormal rotation matrix R that transforms B into F, with B = RF. This general formulation applies to any attitude sensor that relies on baseline observations to derive the platform orientation.
GNSS-based attitude estimation is based on the same working principle: processing code and phase observations to yield baseline estimates, which are then used to estimate the attitude angles. However, instead of using the traditional sequential approach that de-couples ambiguity resolution and attitude determination into two steps, we formulate the estimation problem in order to solve the integer and attitude estimation problems in an integral manner.
To do this, we first formulate the proper functional GNSS attitude model, as will be shown in the following section, then solve it with a new attitude-ambiguity estimation procedure, using the principles of Integer Least Squares (ILS). The method solves for the integer ambiguities by including the whole set of geometric constraints relative to the local baseline frame.
In this way we can achieve a significant improvement in ambiguity resolution performance, although at a computational price: this constrained ILS method is inherently more complex than unconstrained ILS implementations, such as the popular Least-squares AMBiguity Decorrelation Adjustment (LAMBDA) method.
In order to reduce the ILS method’s computational expense, we have developed efficient and numerically fast search algorithms to search for the integer minimizer. We will present results from two flight tests and compare the capability of both the unconstrained LAMBDA and the MC-LAMBDA attitude determination methods.
This novel formulation of the attitude-ambiguity estimation problem can be used to enhance relative positioning solutions, of particular importance for formation flying applications. We discuss these results in the final section.
The GNSS Attitude Model
We cast the set of double-difference (DD) GNSS code and phase observations obtained by tracking n + 1 satellites on a single frequency into a linear(ized) model,
E(y) = Az + Gb; z∈Zn, b∈R3
D(y) = Qyy
where, E(·) is the expectation operator, y is the vector of DD code and phase observations, z is the vector containing the n unknown integer-valued ambiguities, and b is the vector of real-valued baseline coordinates. We limit our treatment to single-epoch scenarios.
. . .
Multivariate Constrained Integer Least Squares
The GNSS attitude model can be solved in the context of the ILS theory. The solution follows two steps: float estimation and attitude-ambiguity estimation.
. . .
MC-LAMBDA: Fast Implementation of Constrained ILS
We devised a fast numerical approach . . . based on the LAMBDA method by exploiting two properties of the cost functions.
First, similar to what is done in the standard, unconstrained LAMBDA method, the ambiguities are decorrelated. This partially mitigates “halting” problems, by reducing the set of independent integer ambiguities which are not contained in the search space, given any initial set of independent integer ambiguities.
Then, in place of the extensive search algorithm, we implement an alternative method based on approximating functions that are easier to evaluate than C(Z).
. . .
A Comparison of Attitude Estimation Algorithms
. . .
An analytical solution has been known since the 1960s only for a diagonal matrix . . . a case known as Wahba’s problem. Various numerically efficient methods have been proposed to solve for Wahba’s problem, such as the QUaternion ESTimator (QUEST), the Fast Optimal Attitude Matrix (FOAM), the EStimator of the Optimal Quaternion (ESOQ) or the Second ESOQ (ESOQ2) algorithms.
Although fast, these methods only approximate a solution…
Application Example: Aircraft Attitude Determination
The newly developed MC-LAMBDA method is being tested on a wide range of platforms, while varying antennas/receivers grade, constellation availability and quality, and platform dynamics. The most interesting test results obtained to this date have been from applying this method to data collected on a flying platform.
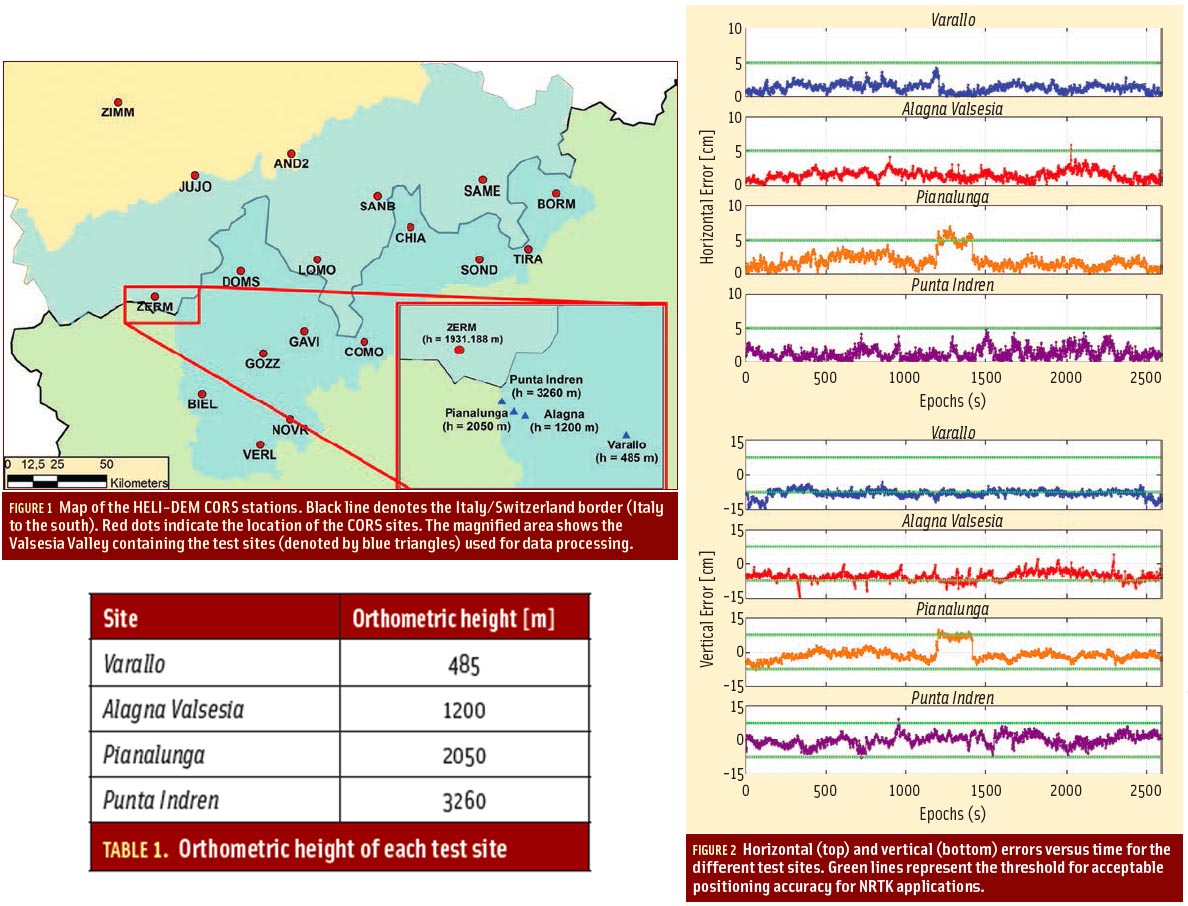
Several flight tests have been performed aboard the Cessna Citation II PH-LAB. This is an aircraft owned and operated jointly by the Delft University of Technology (DUT) and the Dutch Nationaal Luchten Ruimtevaartlaboratorium (NLR, National Aerospace Laboratory) that is equipped with various test systems and facilities, including a selection of GPS antennas.
The first flight analyzed took place on June 2, 2005, in the north of The Netherlands, using a single GNSS receiver connected to three antennas: one placed on the middle of the fuselage, and two L1 antennas — one placed at the end of the left wing and the other on a boom on the nose. The receiver logged one-hertz data during the flight test, between 11:42 and 13:20 UTC (Coordinated Universal Time).
. . .
Attitude-Bootstrapped Improved Relative Positioning
The MC-LAMBDA method, described in the previous section, can be used in other ways, for example, to improve relative positioning in the formation flying.
Traditionally, in multi-platform missions, such as formation flying and rendezvous, the GNSS-based attitude determination and relative positioning problems are treated independently. Recent research has shown that multi-antenna data can also be used to enhance the relative positioning between the platforms.
This approach makes use of an approximation of the ILS by first solving the attitude determination problem for each individual platform with the MC-LAMBDA method and then to use its solution to improve the baseline estimation so that the bootstrapped solution can find the baseline between platforms. This integrated approach is coined attitude-bootstrapped relative positioning.
. . .
Conclusion
We have introduced a new method of GNSS-based attitude determination. Instead of following the classical approach of first estimating the baselines from carrier phase observations and then estimating the attitude matrix, the new MC-LAMBDA method has the orthonormal constraints of the attitude matrix incorporated into the ambiguity objective function from the start.
As a result the a priori geometric information is properly weighted in the ambiguity objective function and provides guidance for the search of the integer minimizer. The increased complexity is tackled by means of easy-to-use bounding functions, which allow for an efficient and fast numerical solution.
By tightening the relation between the attitude and the ambiguity estimation problems, the new method is capable of maximizing the probability of successful integer ambiguity resolution, while making epoch-by-epoch precise attitude solutions available in a timely manner.
The novel ambiguity-attitude estimation method can also be employed to enhance a relative positioning solution between a number of platforms with multiple antennas. When flying multiple platforms in formation, each carrying a number of antennas, reliable ambiguity estimation for the baselines at each platform implies higher redundancy in the inter-platform baseline measurements. This allows for higher probabilities of correctly fixing the ambiguities between the different platforms and more precise baseline estimates.
For the complete story, including figures, graphs, and images, please download the PDF of the article, above.
Acknowledgements
Peter Teunissen is Federation Fellow of the Australian Research Council (project FF0883188). This support is gratefully acknowledged. The research of Sandra Verhagen is supported by the Dutch Technology Foundation STW, applied science division of NWO, and the Technology Program of the Ministry of Economic Affairs. The GAIN experiment team, a mutual cooperation between chairs of Control and Simulation, Physical and Space Geodesy and Mathematical Geodesy and Positioning at TU Delft is acknowledged for the pleasant cooperation during the flight tests. This work is supported by the Australian Space Research Program GARADA project on SAR Formation Flying.
Additional Resources
[1] Buist, P. J., and P. J. G. Teunissen, G. Giorgi, and S. Verhagen, “Multi-Platform Instantaneous GNSS Ambiguity Resolution for Triple and Quadruple Antenna Configurations with Constraints,” International Journal of Navigation and Observation, vol. 2009, Article ID565426, doi:10.1155/2009/565426, 2009
[2] Buist, P.J., P.J.G.Teunissen, G.Giorgi, S.Verhagen, “A Vectorial Bootstrapped Approach for Integrated GNSS-based Relative Positioning and Attitude Determination of Spacecraft,” Acta Astronautica, 68(7-8): 1113-1125, DOI: 10.1016/j.actaastro.2010.09.027. (2010)
[3] Buist, P.J., and P.J.G. Teunissen, G. Giorgi, and S. Verhagen, “Multivariate Bootstrapped Relative Positioning of Spacecraft Using GPS L1/Galileo E1 Signals,” Advances in Space Research, 47(5): 770-785 Scientific applications of Galileo and other Global Navigation Satellite Systems – II, DOI: 10.1016/j.asr.2010.10.001, 2010
[4] Cheng Y., and M. D. Shuster, “Robustness and Accuracy of the QUEST Algorithm,” Advances in the Astronautical Sciences, 127:41-61, 2007
[5] Giorgi, G., and P. J. G. Teunissen, S. Verhagen, and P. J. Buist, “Integer Ambiguity Resolution with Nonlinear Geometrical Constraints”, Proceedings of the VII Hotine-Marussi Symposium on Mathematical Geodesy, Rome, Italy, 2009
[6] Giorgi, G., and P. J. G. Teunissen, “Carrier Phase GNSS Attitude Determination with the Multivariate Constrained LAMBDA Method,” Proceedings of the 2010 IEEE-AIAA Aerospace Conference, Big Sky, Montana, USA, Paper 1103, 2010
[7] Giorgi, G., and P. J. G. Teunissen, S. Verhagen, and P.J. Buist, “Instantaneous Ambiguity Resolution in GNSS-based Attitude Determination Applications: the MC-LAMBDA Method,” Journal of Guidance, Control and Dynamics, accepted for publication, April 2011.
[8] Markley, F. L., and D. Mortari, “How to Estimate Attitude from Vector Observations,” presented at AAS/AIAA Astrodynamics Specialist Conference, Paper 99-427, 1999
[9] Teunissen, P. J. G., and A. Kleusberg, GPS for Geodesy, Springer, Berlin Heidelberg New York, 1998
[10] Teunissen, P. J. G., “Integer Least-Squares Theory for the GNSS Compass,” Journal of Geodesy, 84(7):433-447, 2010
[11] Teunissen, P. J. G., and G. Giorgi and P. J. Buist, “Testing of a New Single-Frequency GNSS Carrier-Phase Attitude Determination Method: Land, Ship and Aircraft Experiments,” GPS Solutions, 15(1):15-28, 2010
[12] Teunissen, P. J. G., “Mixed Integer Estimation and Validation for Next Generation GNSS,” Handbook of Geomathematics, Edited by W Freeden et alia, Part V, 1101-1127, 2010
[13] Wahba, G. “Problem 65-1: A Least Squares Estimate of Spacecraft Attitude,” SIAM Review, 7(3): 384–386, 1965