Q: How do you compute a relative position using GNSS?
A: In many applications the absolute position of an object is less important than the relative position to other objects in the vicinity. An obvious example is a collision avoidance system, wherein the proximity of nearly vehicles is much more important than whether the vehicles are located on street “X” or “Y.”
Q: How do you compute a relative position using GNSS?
A: In many applications the absolute position of an object is less important than the relative position to other objects in the vicinity. An obvious example is a collision avoidance system, wherein the proximity of nearly vehicles is much more important than whether the vehicles are located on street “X” or “Y.”
Although many sensors can be used for determining relative position — for example, radar, lidar, vision and ultra-wideband — GNSS can also be used. In fact, as will be shown later, any form of differential GNSS processing is a form of relative positioning. This includes GNSS attitude determination, vehicle-to-vehicle (V2V) and, vehicle-to-infrastructure (V2I) applications.
Standalone Positioning
Before looking at the relative positioning problem, let’s quickly review the idea of absolute positioning.
The pseudorange to a satellite measured from receiver “a” is given by
Ρ = ρa + ba + εa (1)
where ρ is the geometric range between the receiver and the satellite, b is the receiver clock bias, and ε is the composite measurement error. The geometric range term is a function of the position of the satellite, ⃗rs, and receiver, ⃗ra, and thus equation (1) can be written more explicitly as
Ρ = ρa(⃗rs, ⃗ra) + ba + εa (2)
The geometric range term is a nonlinear function of the desired receiver position, ⃗ra, and can be approximated by linearizing around the current best estimates of the position, ⃗̂ra, as follows
δ
ρa(⃗rs, ⃗ra) ≈ ρa(⃗rs, ⃗̂ra) + ⃗uaTδ⃗ra (3)
where δ⃗ra is the error in the current estimate of the receiver position such that ⃗ra = ⃗̂ra + δ⃗ra. The unit vector, ⃗ua, is defined as
Equation (4) (see inset photo, above right, for equations)
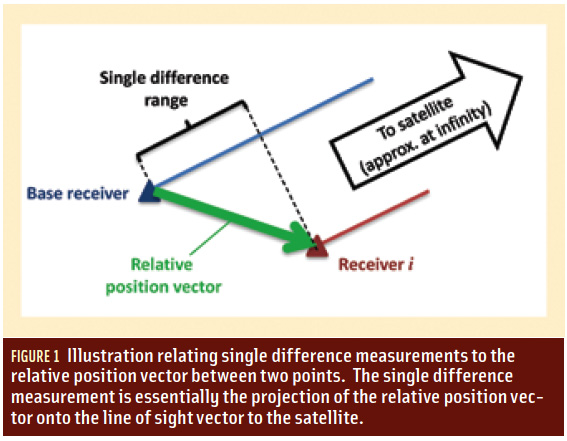
Strictly speaking, this unit vector should be computed from the estimated position vector (i.e., replace ⃗ra with ⃗̂ra), but given the large distances to the satellites and the typically small magnitude of δ⃗ra (we will revisit this point later), the differences can be neglected and the simplified notation, adopted. Figure 1 (see inset photo, above right) illustrates the relationship between the relevant vectors.
Substituting equation (3) into equation (2) and performing some simple algebra gives
Equation (5)
The matrix notation is included to illustrate how the left-hand side can be expressed as a function of the unknowns δ⃗ra and ba for a single satellite. However, by combining observations from multiple satellites, equation (5) forms the basis for computing a recursive least-squares estimate of unknown parameters.
Before moving on, it is worth noting that equation (5) is only a function of the absolute position (error) of the receiver. Correspondingly, standalone positioning is a form of absolute positioning. In the next section, we contrast this case with case of differential positioning.
Differential Positioning
As is well known, differential positioning involves two receivers. Although one receiver — typically called a base station/receiver — is commonly assumed to be located at a known point, this is not a requirement. The following development starts with the case where both receiver positions are unknown. Once this is explored, we will discuss the special case of a known base station position.
Assuming receivers a and b measure pseudoranges at the same time, the between-receiver single difference pseudorange can be written as
ΔΡab = Ρa − Ρb
= ρa(⃗rs, ⃗ra) − ρb(⃗rs, ⃗rb) + Δbab + Δεab (6)
where Δ(•) is the between-receiver single different operator. Using the expansion from equation (3) (with appropriate substitutions for the receiver subscript) and bringing the geometric range estimates to the left-hand side of the equation gives
δΔΡab = ΔΡab − [ρa(⃗rs, ⃗̂ra) − ρb(⃗rs, ⃗̂rb)]
= ⃗uaTδ⃗ra − ⃗ubTδ⃗rb + Δbab + Δεab (7)
With reference to equation (4) and Figure 2 (see inset photo, above right), the unit vector associated with receiver “b” can be written as
Equation (8)
where Δ⃗rab is the relative position vector between receivers “a” and “b.” Substituting this into equation (7) and rearranging gives
Equation (9)
where δΔ⃗rab is the error in the current best estimate of the relative receiver vector. In other words, differential processing provides a direct estimate of the relative position (error), not the absolute position.
Relative versus Absolute Differential Positioning
Let’s return to the idea of a base station receiver at a known location. Assuming receiver b to be the base station, the δ⃗rb term is zero and thus δΔ⃗rab = δΔ⃗ra. Equation (9) then reduces to
δΔΡab = ⃗uaTδ⃗ra = Δbab + Δεab (10)
which is similar to equation (5) in that the terms on the right hand side are only a function of the absolute position (error) of receiver “a.”
The other differences are that we now estimate the relative clock error between the receivers (which is usually treated as a nuisance parameter) and the errors are reduced compared to the standalone case, which, of course, is the main motivation for differential processing.
Most people will be familiar with this approach to differential processing and, not surprisingly, we frequently hear claims that “differential techniques are used to compute the absolute position.” However, the key point is that absolute positioning is a special case of relative positioning in which the base station coordinates are known in an absolute sense.
However, scenarios exist in which the base station coordinates are not known. For such cases, we need to consider all terms in equation (9). To this end, the second term on the right-hand side of equation (9) is effectively an additional error that arises if/when the base station coordinates are incorrect. In most cases, this error is negligible because the denominator is so large — roughly 20,000 kilometers — compared to the numerator.
In particular, for applications such as V2V, V2I and GNSS attitude determination, the inter-receiver distances are generally small, typically less than a few hundred meters. Furthermore, even if the base station position is determined using standalone positioning techniques, the resulting error will almost always be less than 100 meters.
Even if one pessimistically assumes the base station error and the inter-receiver distance are both one kilometer, the second term in equation (9) has a maximum possible value of about five centimeters [= (1 km)2 / 20,000 km], which is quite small (at least for pseudorange measurements).
Where the effect of base station error can become a problem is when very large inter-receiver distances are considered. A few examples of this are included in the M.Sc. thesis by C. Tang (“Accuracy and Reliability of Various DGPS Approaches”, May 1996, University of Calgary, UCGE Report No. 20095, available here).
Summary
The key takeaway from this discussion is that differential processing of GNSS data ultimately produces an estimate of the relative position of the two receivers involved. Only if the base station coordinates are known in an absolute sense are the coordinates of user receivers also absolute in nature.
Another point worth noting is that although the foregoing mathematical development focused on the use of pseudorange measurements, the same development also applies to carrier phase data. The main difference in the latter case is that the carrier phase ambiguity terms need to be included.
Also, because the carrier phase measurement errors are smaller than those of the pseudorange (in terms of noise and multipath), carrier phase processing is a bit more sensitive to base station positioning errors.
We should also note that, even though carrier phase process often uses double differencing techniques, the between-satellite difference does not negate any of the above development.