A look at recent testing and the advantages of using KF tracking to process GNSS meta-signals.
Daniele Borio European Commission, Joint Research Centre (JRC), Melania Susi Topcon Positioning Systems Inc.
Several Global Navigation Satellite System (GNSS) receivers now support at least two frequencies. This includes the availability of dual-frequency measurements from smartphones capable of processing both L1 and L5 frequencies. Effective signal processing from different frequencies is still an active research field with implications both at the transmitter and receiver sides. The second-generation Galileo signals may include a new component into the L1/E1 frequency band, denoted as E1D. While E1D should be shifted at a Radio Frequency (RF) different from the L1 center frequency, its selection will also depend on a receiver’s ability to fully exploit the benefits of signals from different frequencies.
A promising approach to simultaneously deal with signals from different frequencies is based on the so-called meta-signal concept [1] where components from different frequencies are treated as a single entity characterized by common parameters. Recent work from the authors [2] shows that components from two different RFs can be effectively represented using bicomplex numbers. Such representation, which is briefly reviewed in the article, allows the isolation of the three components: a code, a carrier and a subcarrier term. These components can be effectively tracked using a triple-loop architecture, which can benefit from the introduction of a Kalman Filter (KF) exploiting the fact that related dynamics are experienced by the code, carrier and subcarrier components. Moreover, a KF can significantly improve receiver performance under dynamic conditions. This is mainly due to the dynamic model embedded in the KF.
This article, which is based on a recent work of the authors [3], describes the KF tracking architecture developed for GNSS meta-signals using bicomplex numbers. Tests performed under dynamic conditions show the benefits of this type of approach.
Bicomplex Signal Representation
In previous work from the authors [2], it was shown that two GNSS signals modulated into two different RFs can be effectively expressed as the real part of the product of three terms: a code component, a complex carrier and a subcarrier term:
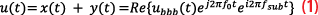
In Equation 1, x(t) and y(t) are the RF signals, which form the sideband components of u(t), the final GNSS meta-signal. f0 and fsub are the center and subcarrier frequencies of u(t) and are obtained as the average and semi-difference of the RFs of the two sideband components, respectively.
Representations (Equation 1) is possible only using bicomplex numbers, which are a four-dimensional extension of complex numbers characterized by two imaginary units, i and j, which square to -1, and a hyperbolic unit, k, which squares to 1 [4]. ubbb(t) is the bicomplex baseband representation of u(t), which is obtained by combining the (complex) baseband representations of x(t) and y(t). Additional details on the bicomplex representation of a GNSS meta-signal can be found in [2].
Signal representation (Equation 1) has fundamental implications for processing a GNSS meta-signal. Indeed, it implies the three components in product (Equation 1) can be processed using three independent tracking loops: a Delay Lock Loop (DLL), a Phase Lock Loop (PLL) and a Subcarrier Phase Lock Loop (SPLL). Each loop tracks one of the three factors isolated in the product in Equation 1. This is a direct extension of standard receiver processing where an additional loop, used to track the subcarrier component, is introduced. The SPLL aligns in phase the power received from the two sideband components leading to a form of coherent signal combining.
In the previous work from the authors [2], the triple-loop tracking architecture was implemented and tested using Galileo AltBOC signals collected with a Software Defined Radio (SDR) front-end. The three loops featured dedicated discriminators operating on the bicomplex correlators obtained by jointly processing the input samples from x(t)and y(t), which were used to reconstruct ubbb(t). Each loop operated independently using separate loop filters. While the advantages with respect to separate sideband processing were clearly demonstrated, this type of architecture does not exploit the relationship between the different Doppler frequencies estimated by the three loops. Moreover, performance can be further improved by assuming a dynamic model describing the time evolution of the different system parameters. For this reason, a KF tracking loop is developed and analyzed.
Triple-Loop Kalman Filter Tracking
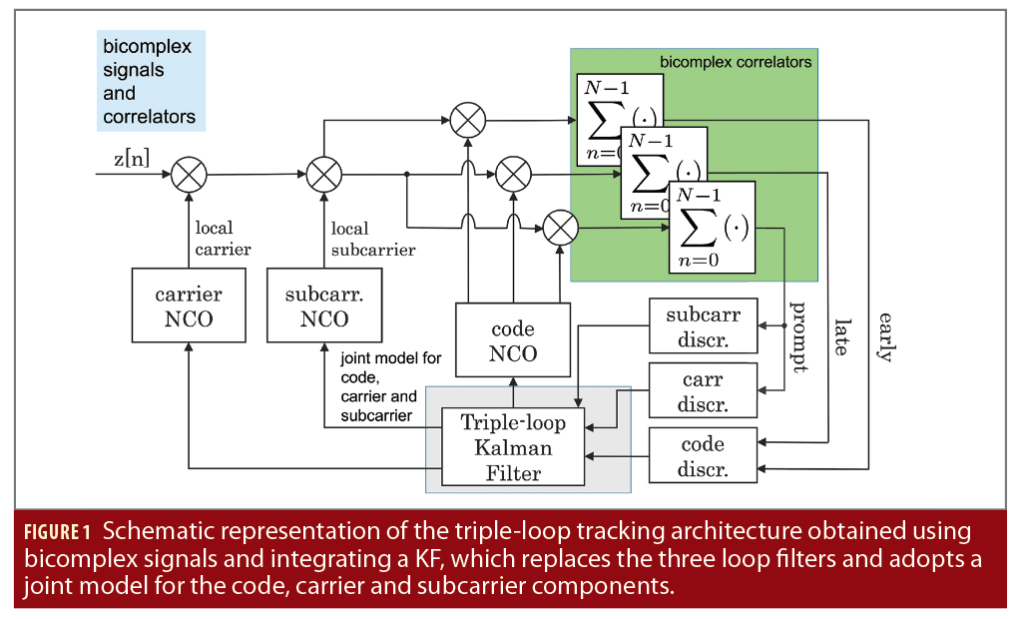
A schematic representation of the triple-loop architecture obtained using bicomplex numbers and a single KF is provided in Figure 1. The input samples, z[n], are a baseband bicomplex representation of the digital signals obtained from the sideband components, x(t) and y(t). In particular,

where ybb[n] and xbb[n] are the complex baseband samples obtained from x(t) and y(t) and e1 and e2 are defined as

In the previous equation, k is the hyperbolic bicomple unit. e1 and e2 are orthogonal and idempotent and their properties are useful to reduce the complexity of bicomplex number operations. Note that ybb[n] and xbb[n] are affected by residual delays and Doppler frequencies, which are estimated by the three loops depicted in Figure 1. z[n] is correlated with local replicas of the incoming signal codes and carrier and subcarrier components. In this way, three bicomplex correlators are obtained: the early, prompt and late correlators. They are processed by the code, carrier and subcarrier discriminators that provide as output noisy estimates of the residual code, carrier and subcarrier errors. Unlike previous work, where three independent loop filters were used, a single KF is adopted in this case to provide the Doppler estimates used to drive local code, carrier and subcarrier generation.
The KF implemented features a five-dimensional state vector:
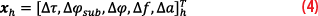
where h is the time index and Δτ, Δφsub and Δφ are the code delay, subcarrier and carrier errors, respectively. Common Doppler frequency and acceleration errors, Δf and Δa, are also considered. Equation 4 is a direct generalization of the state vectors used in KF tracking loops operating on a single signal. In this case, an additional state, Δφsub, has been included in the KF state vector.
The state vector is propagated in time using the following dynamic model

where A is the state transition matrix defined as

where βcode is the ratio between the code and carrier nominal frequencies. βsub is the ratio between the subcarrier and carrier nominal frequencies and Tc is the coherent integration time and update rate of the loop.
wh is a noise vector modeled as white and Gaussian. The covariance matrix of wh depends on several factors including the signal line-of-sight acceleration, code-carrier and subcarrier-carrier divergences and the properties of the local oscillator of the front-end used to down-convert and digitize the input signal x(t) and y(t). Details on the construction of the covariance matrix associated to wh can be found in [3].
The predictions made by the KF using Equation 5 are corrected using the three discriminator outputs that are grouped into the observation vector:

where Dcode, Dsub and Dcar are the code, subcarrier and carrier discriminator outputs. Also, in this case h denotes the time index.
The observation vector is related to the state vector by the following observation model:

with

In Equation 8, vh is the observation noise vector: it is assumed zero mean and Gaussian with independent components. The covariance matrix of vhis determined by the variances of the discriminator outputs, which can be found in [3].
Experimental Setup
The KF triple-loop architecture has been implemented in a custom Python software receiver able to jointly process signals from two different frequencies.
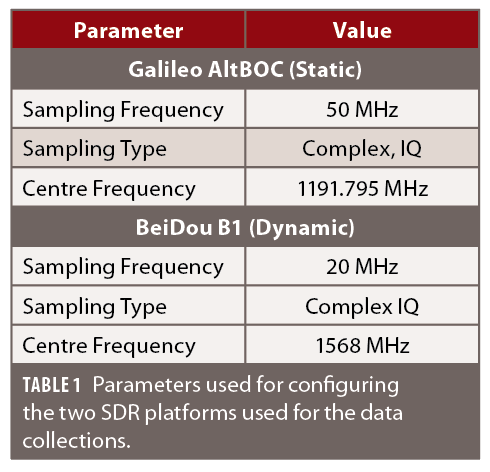
Several tests were conducted to verify the effectiveness of the KF architecture developed. Both static and dynamic conditions were considered. The same datasets authors analyzed in previous work are considered for the static tests. Specific focus is given to the AltBOC modulation, which was collected using a wide-band SDR front-end configured according to the parameters reported in the upper part of Table 1.
The effectiveness of meta-signal KF filtering under dynamic conditions was studied through dedicated data collections performed using a low-cost SDR front-end mounted inside a car. Views of the experimental setup adopted for these tests are shown in Figure 2. The left part of the figure shows the interior of the car with the SDR platform, and a mass-market receiver adopted to collect reference data. Both devices were connected to a laptop and to a patch antenna mounted on the roof of the car. The right part of the figure provides a view of the place selected for the experiment: a long road in an industrial zone close to Turin, Italy. The driver performed several loops along this road reaching speeds around 50 km/hour. Buildings on both sides of the road introduced multipath and other propagation effects.
The dynamic tests focused on the BeiDou B1 meta-signal obtained by combining the BeiDou B1I and B1C components. These components have different spectral characteristics and are received with different power levels. In this respect, the BeiDou B1 combination is one the most general forms of GNSS meta-signals without any specific structure or symmetry. The parameters adopted for configuring the low-cost SDR front-end used for tests are reported in the bottom part of Table 1. A center frequency of 1,568 MHz was selected as it is also at the middle of the center frequencies of the B1I and BIC components, which are 14.322 MHz spaced apart. It is noted that this frequency is the nominal value used to configure the SDR platform. It is well-known that in such low-cost devices a slightly different frequency is actually used for the signal down-conversion [5]. Without proper compensation, the difference between the nominal value and the actual center frequency adopted by the device will lead to a residual Intermediate Frequency (IF), which, in turn, can prevent proper KF tracking loop operations. For this reason, the residual IF was estimated and taken into account in the actual implementation of the KF tracking loop.

Experimental Results
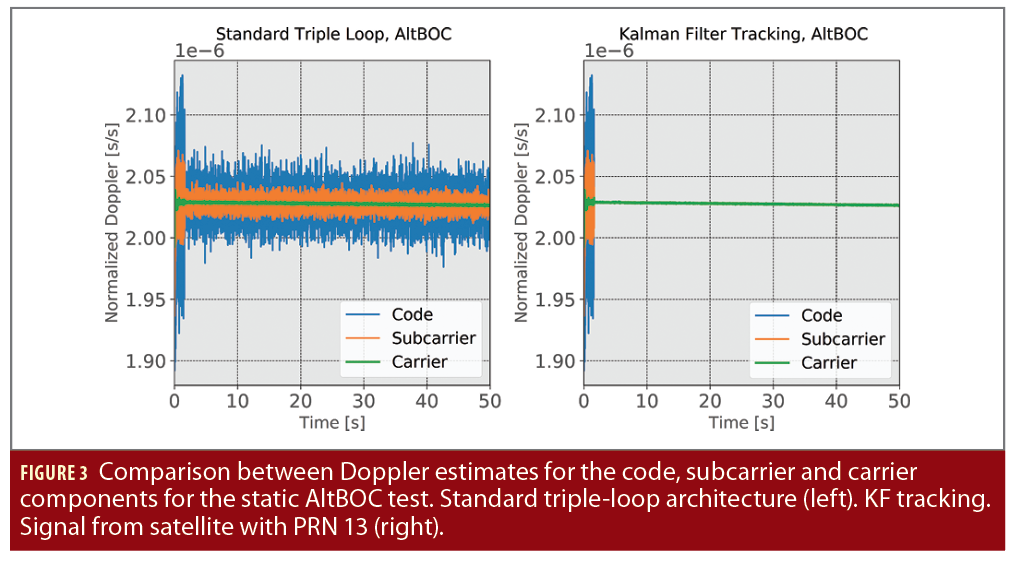
Results obtained for the static dataset with AltBOC signals are considered at first. Figure 3 provides a comparison between the Doppler estimates obtained using triple-loop architectures with standard loop filters and with the KF approach. The two cases are considered in the two parts of the figure. In each part, the code, subcarrier and carrier Doppler estimates are provided, and each component is
normalized by its nominal rate. The results obtained using separate loop filters are shown in the left part of the figure. A third order PLL with a 15 Hz bandwidth was considered along with a second order DLL and SPLL with 2 and 3 Hz bandwidths, respectively. An integration time of 5 ms is adopted after secondary code synchronization. Under static conditions, the standard triple-loop architecture is able to effectively track the different signal components, which overlap justifying the adoption of a KF with single Doppler frequency and acceleration states. KF tracking is analyzed in the right part of Figure 3. After an initial transient, where standards Frequency Lock Loop (FLL)/PLL are used to achieved frequency and phase lock conditions, KF operations are started. A single estimate for the three Doppler components is obtained as it clearly emerges from the right part of Figure 3. The case of signal from the satellite with Pseudo-Random Number (PRN) 13 is considered.
The use of joint Doppler states does not affect lock conditions as it clearly emerges from the analysis of the Carrier-to-Noise power spectral density ratio (C/N0) provided in Figure 4. The C/N0 has been estimated considering the ability of triple-loop architectures to align in phase the signals and correlators from the two sidebands. The C/N0 is used here as a lock indicator showing the SPLL’s ability to effectively align in phase the two sideband prompt correlators. In this case, the two loop architectures achieve similar performance and practically identical C/N0 values are found in the two cases. This is expected as the real advantages of a KF tracking loop are found under dynamic conditions. A static scenario has been considered mainly to preliminary check the proper functioning of the implemented KF tracking loop.
During the dynamic test, a total of 10 BeiDou satellites were visible. Three of them, the ones with PRN 11, 12 and 13, broadcast only the BI1 component and thus are not considered. The signals from satellite PRN 37 were very weak and received in a discontinuous way. While it was possible to acquire them, stable tracking was never achieved with any of the methods implemented. For this reason, only the remaining six signals are considered. The C/N0, obtained for the different BeiDou B1 meta-signals, is depicted as a function of time in Figure 5. Satellites with PRN 34, 42 and 43 have high-elevations and are only marginally impacted by buildings. Periodic drops in the C/N0 of the signal from satellite PRN 43 are clearly visible and correspond to the maneuvers made by the car to invert the direction of motion and perform the loops. During these maneuvers, the vehicle approaches the buildings on the roadside and signal reception is further impaired. A periodic pattern, corresponding to the different loops performed by the vehicle, is also visible in the C/N0 time series of the signal from PRN 42.
Signals from satellites with PRN 22, 23 and 25 are much weaker and significantly impacted by vehicle dynamics. Despite this fact, the proposed tracking architecture allows one to maintain the lock on the three meta-signals.
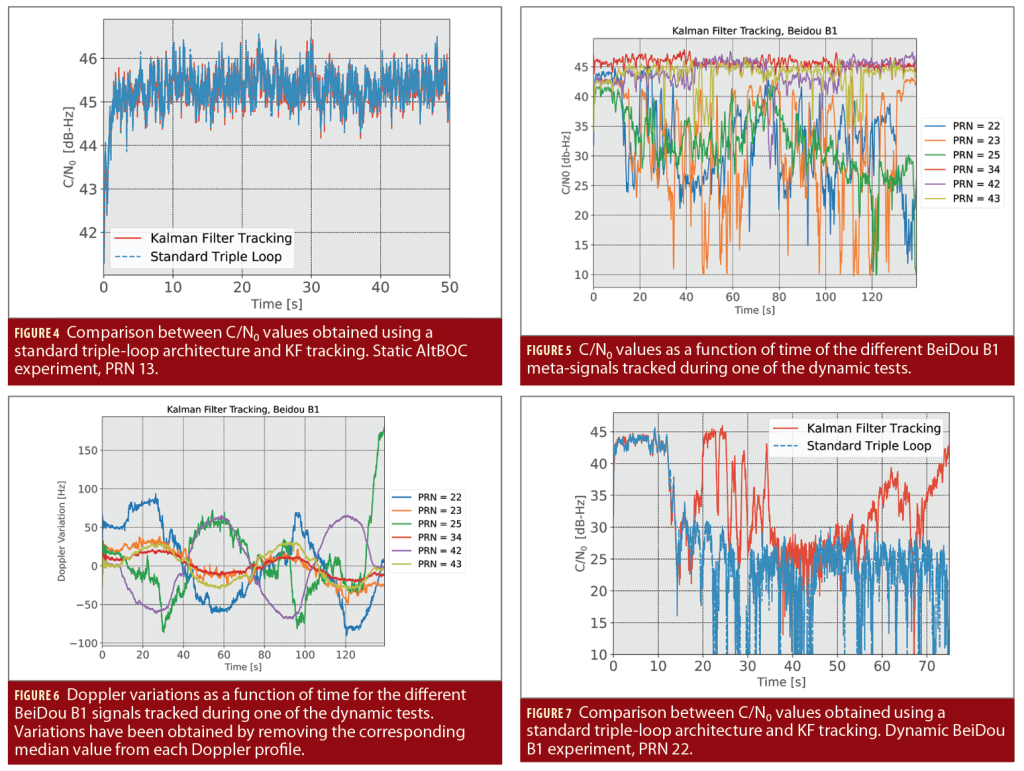
This is because of the combined use of bicomplex signal tracking, which allows recovery of all the available signal power, and KF, which allows one to cope with dynamics and continue tracking even when very low signal power is available. This is the case of the signal from PRN 23, which experiences severe drops in the C/N0 values. Even if these drops last a few seconds, lock conditions are not lost and the KF successfully propagates the signal parameters allowing the recovery of C/N0 values above 35 dB-Hz. When such medium-high C/N0 are realized, valid code, carrier and subcarrier discriminator values are obtained and allow for effective KF measurement updates. The ability of the proposed KF meta-signal tracking architecture to maintain signal lock under challenging conditions is further studied in Figure 6, which shows the Doppler variations of the different BeiDou B1 meta-signals tracked during the dynamic test. Doppler variations have been obtained by removing the median value from each Doppler frequency profile estimated during the experiment. Doppler variations have been considered only to improve Figure 6’s clarity and highlight the periodic patterns generated by the loops the vehicle performed. Indeed, the Doppler frequencies estimated by the KF for each signal assume very different values and, without removing the median values, would have hidden the variations due to the vehicle motion. The fact lock on signal with PRN 23 was maintained during the full duration of the test clearly emerges from Figure 6. The corresponding Doppler variations are smooth and have the same period of those obtained for the other signals.
It was not possible to obtain similar results using the triple-loop architecture with separate loop filters. Even if different loop bandwidth and coherent integration time combinations were tested, it was not possible to achieve continuous tracking for the signals with PRN 22, 23 and 25 and in all cases, an early loss of lock occurred. This is highlighted in Figure 7, where the case of a signal with PRN 22 is considered.
A 25 Hz bandwidth with a 1 ms coherent integration was adopted to improve the dynamic loop response. Despite this fact, loss of lock occurs after about 17 seconds from the start of the experiment: the C/N0 assumes low values and the estimated Doppler frequencies (not displayed in this article) diverges. As already mentioned, several bandwidth/coherent integration time combinations were tested, always achieving results similar to those shown in Figure 7. KF tracking, on the contrary, can maintain lock on the signal even if a coherent integration time equal to 10 ms was adopted. These results show the real advantages of triple-loop KF tracking.
Conclusions
In this work, the performance of a triple-loop architecture, designed using the bicomplex number paradigm, has been further improved by introducing a KF, which exploits a state transition model to track dynamics and jointly process the code, carrier and subcarrier components resulting from the bicomplex representation. While bicomplex numbers are effective for jointly representing and processing signals from different frequencies, the KF fully exploits the fact that related dynamics are experienced by the different signal components.
The proposed architecture has been implemented and tested using real Galileo AltBOC and BeiDou B1I/B1C meta-signals, under both static and dynamic conditions. The data collected have been processed using a custom Python software receiver implementing KF tracking. The analysis clearly shows the advantages of KF tracking for processing GNSS meta-signals. This fact is particularly evident from the tests conducted under dynamic conditions: the KF allows one to continuously track weak GNSS signals received from a moving vehicle. These results are not achievable using standard loops, which require large bandwidths and short integration times to cope with high dynamic conditions.
Manufacturers
The wideband front-end adopted for the AltBOC data collection is a Universal Software Radio Peripheral (USRP)-2944R from National Instruments. The front-end adopted for the dynamic tests with the BeiDou B1 signals is a HackRF One from Great Scott Gadgets. The mass-market receiver used as reference is a Ublox F9R.
References
(1) Issler J.-L., Paonni M., and Eissfeller B. (2010), “Toward Centimetric Positioning Thanks to L- and S-band GNSS and to meta-GNSS Signals”. Proc. of the ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing (NAVITEC), Noordwijk, Netherlands.
(2) Borio D. (2022), “Adopting Bicomplex Numbers for GNSS Meta-Signal Processing”. Inside GNSS, November/December, Vol. 17, No. 6, pp. 48-53.
(3) Borio D., Susi M. (2023), “Bicomplex Kalman Filter Tracking for GNSS Meta-Signals”. Proc. of the ION International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+), Denver, CO.
(4) Alpay D., Luna-Elizarrarás M. E., Shapiro M., and Struppa D. C. (2014). “Basics of Functional Analysis with Bicomplex Scalars, and Bicomplex Schur Analysis.” Springer Briefs in Mathematics. Springer, Cham, Switzerland AG.
(5) O’Driscoll C. and Curran J. T. (2018). “Carrier Phase Tracking Considerations for Commodity SDR Hardware.” Proc. of the International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+), Miami, Florida (FL)
Authors
Daniele Borio received an M.S. degree in communications engineering from Politecnico di Torino, Italy, and an M.S. degree in electronics engineering from ENSERG/INPG de Grenoble, France, in 2004. He received a doctoral degree in electrical engineering from Politecnico di Torino in April 2008. From January 2008 to September 2010, he was a senior research associate in the PLAN group of the University of Calgary, Canada. Since October 2010, he has been with the European Commission Joint Research Centre (JRC). He is currently a scientific technical officer in the JRC Food Security Unit where he supports the European Common Agricultural Policy (CAP) through the European satellite programs, Galileo and Copernicus.
Melania Susi received her B.E. in Mathematical Engineering from the Università TorVergata di Roma, Italy, and M.Sc.s in Telecommunication Engineering and Geomatic Engineering, from the Università of L’Aquila, Italy, and from the University of Calgary, Canada. She holds a Ph.D. in Engineering Surveying and Space Geodesy from the University of Nottingham, UK, where she was also a Marie Curie fellow. After being a scientific technical officer at the Joint Research Centre (JRC) of the European Commission, she is now a GNSS senior researcher at Topcon in Concordia, Italy.