Robustness to GPS jamming and spoofing is critical for military applications yet challenging, and numerous alternative sensing techniques have been explored over the years. Virtual aiding methods have proven effective, with the ability to constrain and localize the search space for improved operability in GPS-denied environments.
By SHAHRAM MOAFIPOOR, BRAD DESPRES, ROBERT STADEL, AEVEX AEROSPACE, GEODETICS PRODUCTS
JIM FITCH, LINQUEST CORPORATION
To achieve mission success, accurate and reliable Position, Navigation and Timing (PNT) information is vital in military applications. But a “silver-bullet” absolute-positioning system that can replace GPS and the capabilities it offers doesn’t exist yet, and the alternatives that are available are platform/sensor specific.
The most promising low SWaP-C systems for Assured PNT include relative aiding sensors such as vision (active LiDAR, passive EO/IR camera), air/wheel speed sensors and other dead-reckoning sensors (magnetometer, barometer). As actual physical devices, they are subject to the usual practical requirements for integration into a PNT system, including reconfigurability (plug & play), resiliency to jamming, autonomy-level, deployment feasibility, computational burden, latency and compensation thereof, interdependency, efficiency and affordability.
In this article, we look at the developments of intelligent virtual aiding methods that extend the perceptive space and acuity of physical aiding sensors through the use of knowledge-based systems considering vehicle type, environmental conditions, coverage area and dynamic range.
The Approach
The intelligent virtual aiding capabilities developed and tested are in the form of vehicle physical property modeling, for example non-holonomic vehicle-type constraints (NHC), virtual altitude constraints and virtual speed aiding. The term intelligent represents the transition from conventional relative aiding-sensors to dynamic navigation using knowledge about the dynamics of the vehicle-motion.
Our approach uses knowledge-based systems and AI methods, including artificial neural networks (ANN). The concept of a virtual measurement is central to this. In this context, a virtual measurement is a computationally derived, sensor-fused, knowledge-infused interpretation of an input space that, when taken collectively, can construct higher-level percepts of the space.
Because of the complexity of collecting such knowledge-infused data for different platforms operating at different environments with different scenarios, the logical step is to build a modeling and simulation environment for training the AI/ML for virtual aiding. This environment should be able to model vehicle dynamics, create different motion dynamics, and simulate environments
The principle of non-holonomic constraints and its algorithms are briefly addressed. The complementary Zero-Velocity-Update (ZUPT) aiding and virtual altitude constraint aiding are also covered. The main contribution of these virtual sensors is to aid land and sea platforms. For more dynamic platforms such as aircraft, virtual-speed aiding has been developed. For the experimental tests, a variety of simulation and real-world tests were performed.
A supervised machine learning agent such as an ANN can be used to learn an improved forward function and capture additional domain knowledge of vehicle dynamics based on fusion of observable variables and optimally estimated hidden ones. This work explores feature vector spaces and various transformations of them to address problems of “the curse of dimensionality,” getting stuck in local minima, overfitting and convergence time. The Kalman filter separates signal from noise, propagates state knowledge based on pre-programmed dynamic system behavior models, optimally estimates the inverse function of hidden, causal, independent variables from observable, dependent ones, and is the de-facto standard in navigation and guidance processing, but remains vulnerable to conditions where the availability of GPS observations is impeded.
Robustness to GPS jamming and spoofing has driven a long history of alternative sensing techniques in military applications. This work demonstrates the effectiveness of virtual sensing methods to constrain and localize the search space in the state estimation task inherent in navigation processing and to permit better operability in GPS-denied conditions and environments. It is part of our effort to add robustness and resiliency in high-risk scenarios such as GPS spoofing/jamming during aircraft landing.
Virtual Non-Holonomic Constraint (NHC)
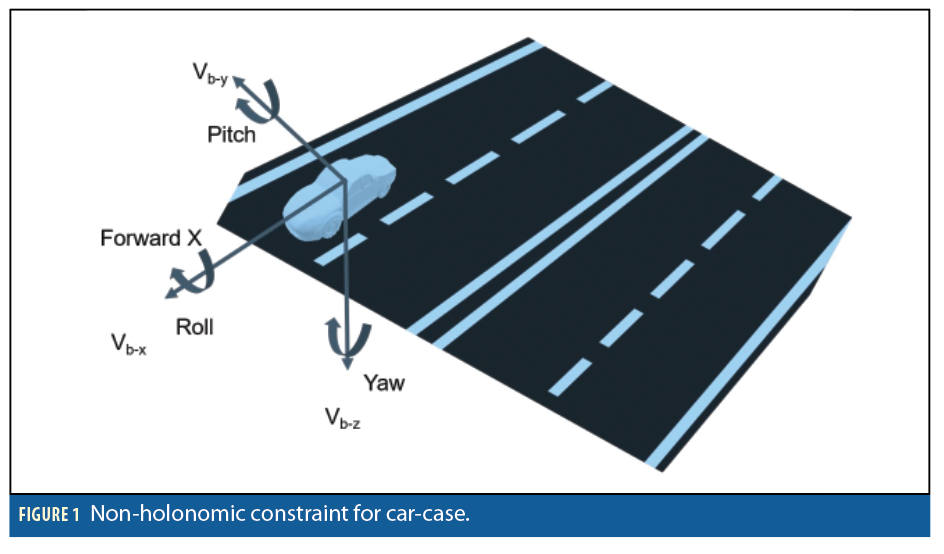
In military applications, external sensors used for the aiding of inertial units have taken on many forms, including Doppler radar, camera and star trackers to name a few. Because GPS does not require a dynamic model, the IMU/GPS navigation suite is independent of vehicle kinematics. It is shown that the rate of growth of the error in position estimates obtained from an IMU can be substantially reduced when a vehicle model with motion constraints is used. This is clearly of value when external information, for example, from GPS, is not available for extended periods due to signal degradation and outages. Figure 1 shows the general architecture of the vehicle-model.
A vehicle is often limited in how it can move. While a specific position and orientation (i.e., a pose) may be achievable, a vehicle’s mobility mechanism often limits its ability to reach the pose without careful maneuvering or judicious use of its available degrees of freedom. Considering a vehicle whose movement is limited to only the forward/reverse direction along the X axis in body frame and not in the Y and Z axes, NHC can be written as:

where, Rnb is the rotation matrix from the local navigation frame, n-frame, to platform body-frame, b-frame, vn is the vehicle velocity vector in the local n-frame. Equation 1 can be re-expressed as:

where, is the computed velocity in the b-frame,
is the actual rotation matrix affected by errors. Equation 2 represents the measurement model fed to the Kalman Filter estimator to constrain the speed along the transverse and vertical velocity components. As noted, the
vehicle motion considered here is constrained to roll in the direction that its wheels are pointing without sideslip.
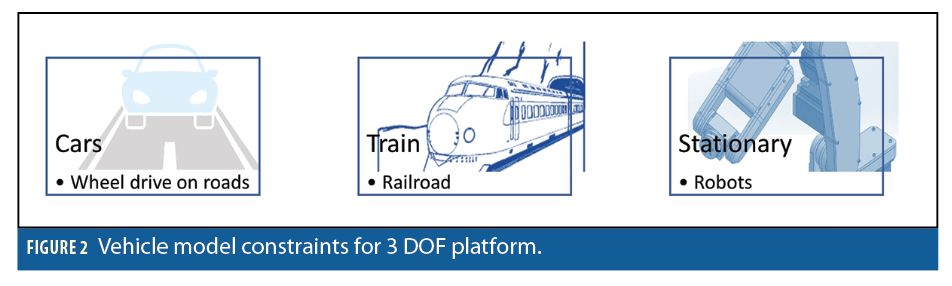
The non-holonomic constraint is practiced in three general cases: 1) updating the navigation solution along with GPS, (2) updating the navigation solution during GPS outage (GPS denied), 3) tight-coupling updates. The developed algorithm was tested on three types of ground platforms: wheeled cars, trains and low-to-no motion platforms (e.g. machine tool), as shown in Figure 2.
Besides development of the generic NHC model, the main difference of implementing this constraint on different platforms is on the measurement error models, marked as Ry and Rz, respectively for each platform case.

We adopt different values for eyb and ezb based on platform-type. For trains and stationary platforms, the constraints are much tighter than for road vehicles.
Complementary ZUPT
In addition to the NHC, we apply the Zero-Velocity-Update (ZUPT) to the vehicle when it comes to rest. This constraint mitigates the navigation drift along all axes and is a critical part of the process. The static ZUPT is also important for controlling the INS error accumulation when prolonged or frequent losses of GPS signals occur.
In this work, we use a combination of accelerometer and gyro raw data to detect stationary periods. The ZUPT can be incorporated into loosely and/or tightly coupled GPS correction and NHC. Additionally, ZUPT can be performed at vehicle stopping points to provide additional velocity error mitigation, facilitating the static calibration of IMU sensor errors as well. To implement the ZUPT, one needs to expand Equation 1 to all axes:

In real-time operations, when the system must also handle GPS and IMU latency, the next question that should be addressed is how frequently should a ZUPT be performed? In answering this question, it should be noted that for prolonged GPS outages, a ZUPT should be performed every 1-2 seconds when using a tactical-grade IMU. This periodicity, however, can vary as a function of the acceptable level of error for a particular application, and the precision of the GPS solution method. Most obviously, this time should be long enough before the INS position error accumulation becomes excessive.
Although performing the ZUPT reduces positioning error growth significantly, especially in the horizontal, the improvement in vertical precision is less pronounced. Similarly, it cannot improve the attitude error. To improve the vertical channel calibration and attitude errors, some other means of external aiding to the vertical channel and the heading must be used, such as a digital barometer and/or a magnetometer compass. In this article, this issue is addressed by using the virtual altitude constraint.
Virtual Altitude Constraint
The NHC can constrain the speed change along the vertical direction, but it cannot constrain gradual altitude changes. Controlling the lateral and vertical velocity in the body frame can only reduce horizontal positioning errors.
For altitude constraint, we can use the virtual altitude constraint as well. When GPS is lost, the latest recorded altitude is used as aiding altitude data. For wheeled vehicles, altitude changes relatively slowly over short time frames, but significantly over longer periods, to the extent of a prolonged GPS outage. Thus, using a fixed altitude constraint does not apply.
On the other hand, for platforms such as a surface vessel, the fixed-altitude assumption may apply. We tested the height-constraint on all ground vehicles, as shown in Figure 2. The main challenge other than the constraint model is to incorporate altitude observation into the global position estimate. The optimal state estimator used in this work represented the position estimates in global ECEF Cartesian XYZ coordinates. Altitude data requires an ellipsoidal model to convert to global position coordinate for aiding. Equation 5 shows the principles of converting virtual altitude to position coordinates:

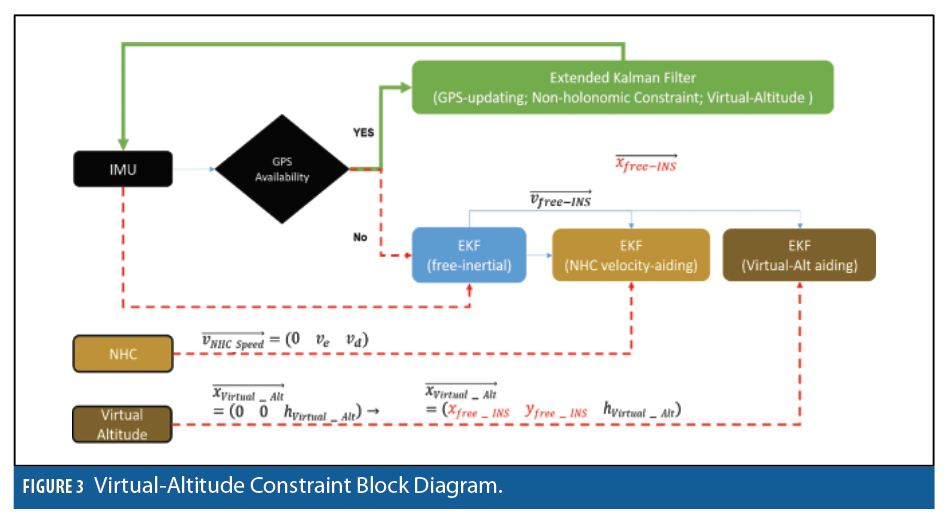
where, N is radius of curvature at the prime vertical, φ and λ are the latitude/longitude components, e is the first eccentricity, and hVirtual-Alt is the virtual-altitude value. Latitude/longitude components are dependent on initial position before the aiding and so the altitude constraining the coordinate is itself dependent on position. This reciprocal dependency problem is more pronounced after running in a prolonged GPS outage, in which horizontal positions can drift. Using this horizontal position to reconstruct the position-aided vector can cause a correlation between the observation and the prediction model. This problem can potentially be solved using NHC aiding to mitigate the horizontal position error. The overall mechanism to reconstruct the position-aiding vector based on virtual-altitude is shown in Figure 3.
Virtual Speed Aiding
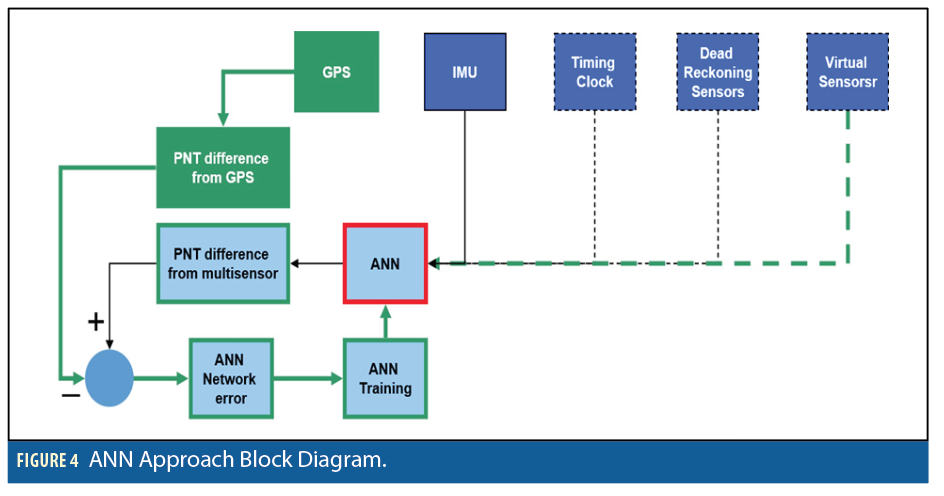
Although for 2D and/or 3D platforms several constraints can be imposed on the moving platform in terms of side speed, down speed, or altitude changes, the problem is more complicated for a 6D platform. An effective representation of vehicle dynamics is the most important factor here. The block diagram of the proposed ANN coupled system is shown in Figure 4. When GPS is available (green), the navigation filter update stage occurs at every GPS epoch using the solution difference between GPS, INS and other engaged sensors. Thus, the navigation filter generates the corrections needed to mitigate INS errors. In this approach, the ANN has inputs covering the minimum training set discussed earlier. The output of the ANN is the change of speed solution.
We used a feed-forward multi-layer perceptron network (MLP) with interior hidden layers for this task. Our ANN coupled system can learn navigation behavior patterns from the experience when GPS is used to mitigate the INS sensor errors and train the ANN. These patterns are then employed to correct the IMU during GPS outage in the form of virtual speed-aiding. At this stage, the ANN is also trained using all sensor states as input and solution differences between the current and the previous update solution at the output. When GPS is lost, the system bypasses ANN training and estimates the change of velocity differences (red). The air-speed solution is calculated as the integration of the ANN predictions starting from the last GPS-provided velocity solution.

ANN Structure
The main property of ANN structures is that they map the input/output relationship based on the observability-level of data. We take advantage of this property to enhance the performance of the navigation filter during GPS outage by using the ANN to provide an accurate dynamic prediction model.
The critical question in developing an ANN is how well it approximates a function that is not part of the training set. ANN, like other flexible nonlinear estimation methods, can suffer from either underfitting or overfitting. Thus, to establish our ANN network for modeling the non-linear platform dynamic prediction model, it was first necessary to provide parameters that accurately represent the platform dynamics. This is called platform dynamic parameterization.
Our previous work in this area has shown the minimum training set for representing platform dynamic variations includes accelerometer signature and gyro angular rate changes. In what follows, we discuss the approach for using ANN for dynamic modeling, as well as the associated training required for aircraft platform. Equation 6 shows the general dynamical model for flight vehicles:

where, are due to the forces acting on the platform, the gravitational acceleration components of the platform in the body-fixed system are expressed by the second term, in which g is the average gravity, β and γ represent the pitch and roll angles,
is the derivative of linear velocity vector, w is the rotation rate along three axes, and v×w is the cross product expressed due to the rotation rates.
In this work, the knowledge acquired from the physical sensors represents the vehicle dynamics in a form of descriptive definitions and classes of objects, as well as their interpretations. Considering the elements in Equation 6 and measurements produced by our Assured PNT sensors, the critical dynamic parameters used to parameterize the vehicle dynamic modeling functions were chosen to be 1) change in raw accelerometer/gyro, 2) acceleration signatures projected along the trajectory vector, 3) change in attitude, and 4) absolute attitude.
A supervised, deep-multi-layered perceptron machine learning agent can be used to learn an improved forward function and to capture additional domain knowledge of vehicle dynamics based on fusion of observable variables and optimally estimated hidden ones. Once the ANN architecture was designed, ANN was trained using a batched-based backpropagation algorithm. Gradient descent and its variants are a common means of network learning from training errors. After training, the ANN prediction corrections were used to compensate the inertial solution during GPS outages. Transformation of the feature space addresses the curse of dimensionality and performs faster coverage of the state space in learning.
ANN Structure for Virtual Speed Scenario
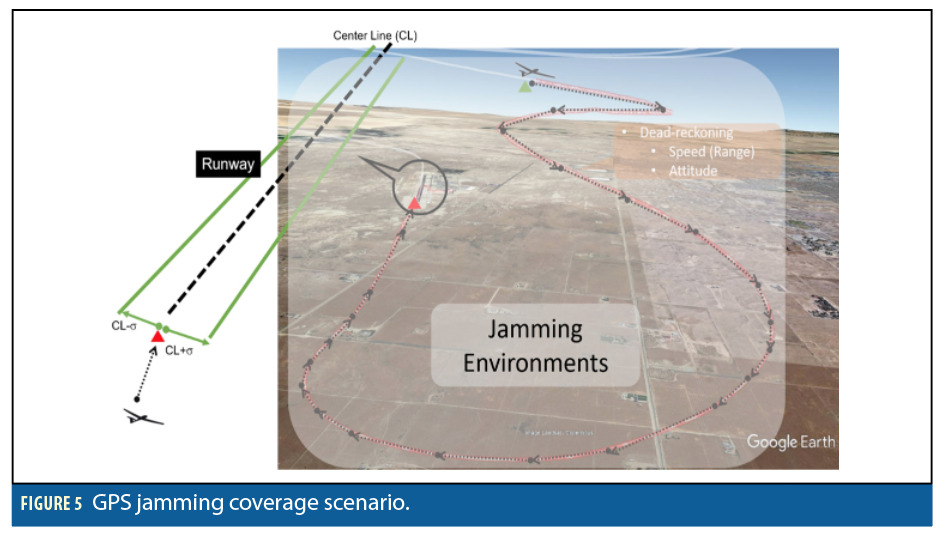
Considering the sensor availability for this study and diversity of aircraft dynamics during different phases of a flight, we concluded that finding a generic set of input parameters for training the virtual speed aiding ANN mechanism that can estimate accurate speed during all phases in a flight is not an effective approach. Instead, training would be optimum for individual maneuver phases, such as takeoff, landing, climbing, etc., with the landing phase being a practical target for study as GPS signals are more likely to be jammed or spoofed around airports. Figure 5 shows the simulation of an aircraft approaching the airport requiring a specific accuracy with respect to the runway in GPS denied conditions for successful landing. This accuracy is denoted CL ± σ, with respect to the centerline of the runway in Figure 5.
Referring to the ANN block diagram in Figure 4, once the platform is subjected to GPS denial, the aircraft trajectory reconstruction switches from PNT-ANN aiding to dead-reckoning point-to-point dynamic reconstruction, where the virtual ANN-generated ∆|v|. provides speed estimate updates along with calibrated gyro for attitude. The ANN is trained to estimate the velocity magnitude difference, ∆|v|. In other words, the speed solution difference is a function of PNT states of the navigation system at the previous epoch, and the integral of speed changes of the current epoch:
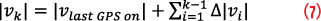
Building a Training Environment
Because of the complexity of collecting knowledge-infused data for different platforms operating at different environments with different scenarios, the logical step is to build a modeling and simulation environment for training the AI/ML for virtual aiding. This environment should be able to model vehicle dynamics, create different motion dynamics and simulate environments.
To practice this feasibility, the proposed system is structurally implemented in the GPS Interference and Navigation Tool (GIANT) system. GIANT is a many-versus-many constructive and repeatable mission-level simulation that evaluates the impact of PNT system performance and operational effectiveness in a benign or electronic combat environment. The main advantages of this system are the capability of simulating GNSS and non-GNSS space vehicle signals, jamming environments, complementary navigation, terrain, system hardware, and IMU measurements.
GIANT provides physics-based GPS and IMU navigation error metrics such as pseudorange error, pseudorange rate error, and position, velocity, acceleration and body rates. GIANT provides true dynamics (position, velocity, acceleration, attitude and attitude rates) as well as the errors for each of those as reported by the navigation system model, for loosely and tightly coupled GPS-INS configurations.
The power of using GIANT for training AI/ML intelligent virtual aiding systems such as proposed here lies in the utilization of knowledge of vehicle dynamics, as well as the changing dynamics in various environments.
With this, the task of producing training inputs is transferred from the real world to the simulated world, which cuts costs and allows more coverage of the input space with scenarios.
The main sensors used in our architecture are an inherited inertial measurement unit (IMU), barometer, odometer and terrain sensor. Our architecture uses other non-inertial sensors, used separately or as a collaboration set, which aid the IMU by providing reference position/velocity/attitude information.
Data Demonstration
Tests and experimental data demonstrations started with the collection of simulated (wheeled, train, vessel, aircraft) and later real-world datasets. The objectives were to test under as many conditions as possible including various vehicle dynamics and IMU sensor grades across many different platforms. The data analyses show system performance using a variety of IMU-grades, from low-grade MEMS to navigation-grade. Table 1 summarizes the tests conducted with specific system configurations.
Virtual NHC-ZUPT-Altitude Aiding
After completing simulations on pre-collected vehicle/vessels/train datasets, the algorithm was tuned for different platforms. Starting with road vehicle tests, Figure 6 shows the different AEVEX Aerospace–Geodetics Product Line Assured-PNT (Geo-APNT™) systems, configured with different IMUs for this study. Geo-APNT is a navigation system that combines a GPS receiver, additional timing source and GPS-aided inertial sensor.
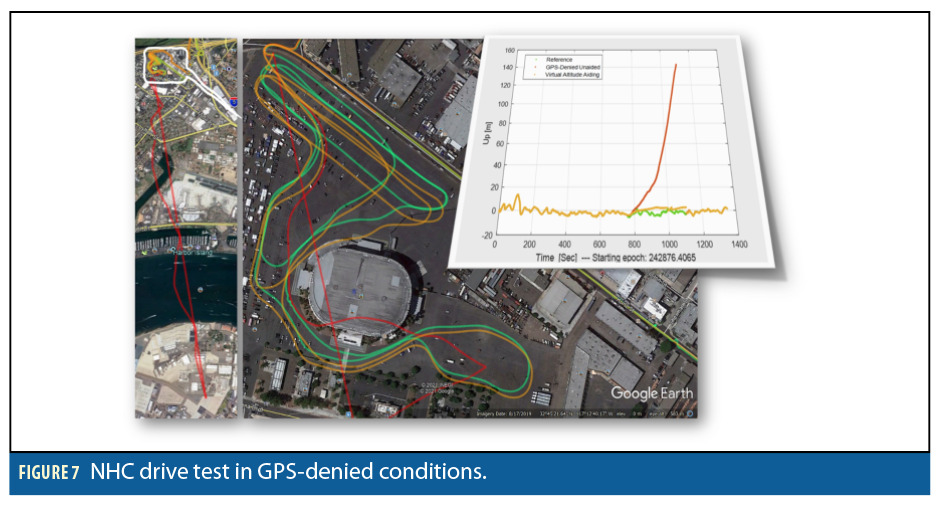
To induce GPS outages during drive testing, an adjustable attenuator was used. This setup allows the system to impose actual/live GPS outages, which is critical for handing all real-time time latency compensations across sensors and software. The first drive test was conducted in an empty parking lot, where the vehicle was driven around non-stop for up to 30 minutes. As shown in Figure 7, the non-aided navigation solution (red) drifts away by kilometers during GPS outages, while the NHC aided solution (orange) could hold the trajectory close to the unimpeded one (green) over the course in real-time.
For testing in conditions with spotty GPS coverage, we performed drive tests in a downtown area with many buildings obscuring visibility to the satellites. We found the ZUPT algorithm is also necessary to constrain the forward speed when the vehicle comes to full stops at traffic lights. A combination of NHC and ZUPT test results in downtown San Diego is shown in Figure 8.
As can be seen, frequent GPS outages, ranging from 1 minute to 30 minutes, were applied during the drive test. Segments with good GPS reception are marked in black; red is the unaided navigation solution travel (free inertial); green is the reference solution, and orange shows the NHC-aided results during drive tests. Similar tests at different locations showed consistent improvement better than ±5m during up to 30 minutes of GPS outage.
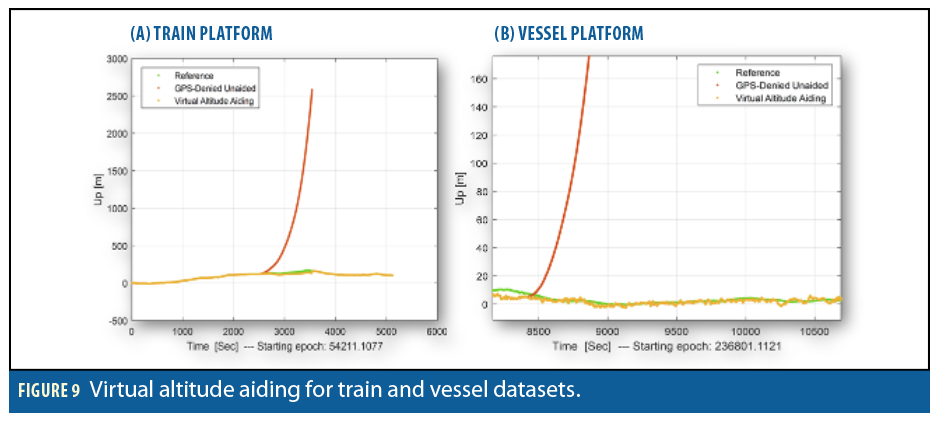
Virtual altitude aiding, as previously discussed, cannot provide a reliable altitude for travel in large areas. For a level parking lot, as shown in Figure 7, the virtual altitude can maintain the altitude at a reasonable value. However, when driving around a wide area, the results were not acceptable. On the other hand, for the train and/or vessel cases, the virtual altitude aiding can maintain the altitude accurately during GPS outages even for prolonged periods, on the order of 30 minutes. This result can be seen in Figure 9.

Virtual Speed Aiding
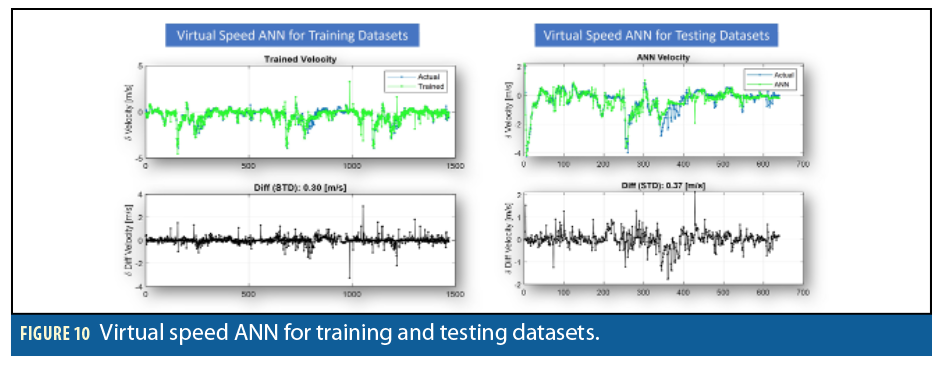
For training the ANN, we used a series of flight datasets collected by an F4 Phantom 2 aircraft. The aircraft was equipped with a Geo-APNT with tactical grade Honeywell HG1700 AG-71 IMUs. During flight data collection, the system was exposed to several low and high-dynamic flight scenarios, including inside loop, outside loop, chandelle and Cuban-eight. Although these dynamics can potentially be used for training the ANN, special attention was placed on the landing approach portions of each flight. To this end, we chose the landing parts of six flights for the training sets and reserved one dataset for the testing to evaluate the ANN performance. Figure 10 summarizes the ANN training/testing results.
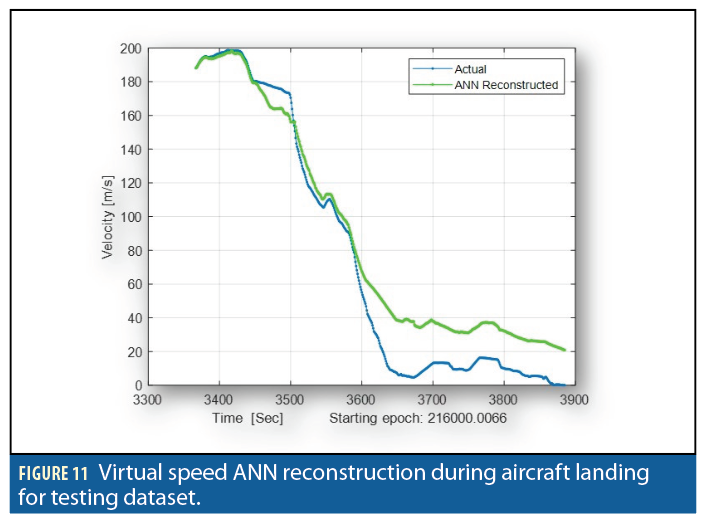
Referring to Figure 10, the left-top plot shows the results of the ANN for learning the change in vehicle dynamics, representing it as change in speed, Δ|V|, and the difference between the training results and the actual data is shown in the bottom plot. A standard deviation of 0.3m/s resulted after training using vehicle special dynamic parameterization. Engaging the trained ANN model and applying it to the platform dynamics for the testing dataset, Figure 10 (right top) shows the overall performance. The difference between the actual change in speed and the ANN-produced value is about 0.37m/s standard deviation. Starting from the last epoch of GPS availability and accumulating the change of speed derived from the ANN outputs, as explained in Equation 7, the reconstructed ANN speed can be seen in Figure 11 in comparison to the actual one.
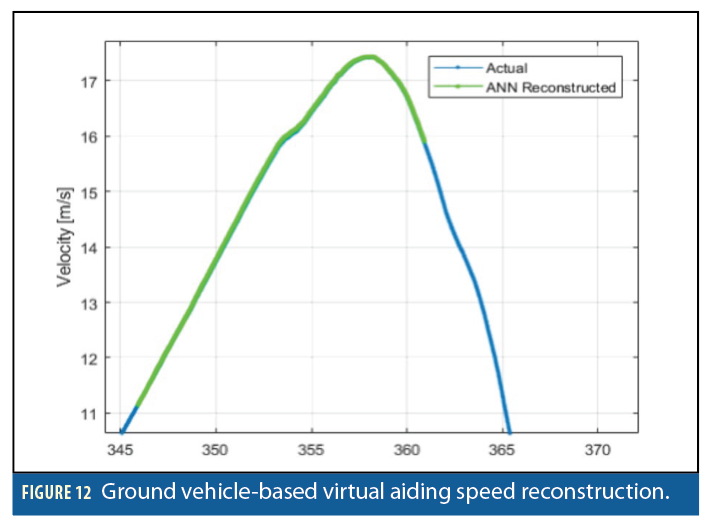
Further tests showed the benefits of the virtual aiding sensors during GPS outages for ground vehicle-based platforms as well. Simulation results show the ANN is less sensitive to the level of noise added to the input measurements for wheeled vehicles. Figure 12 shows a sample for the vehicle-based ANN speed reconstruction.
The next test was to check the impact of the virtual speed aiding on a ground LiDAR mobile mapping system, in which the system was exposed to frequent GPS outages. Figure 13 shows the mobile trajectory undergoing a GPS-challenged environment. Without external update, the geo-referenced LiDAR points experienced drift (yellow), while the corrected trajectory yielded accurate geo-referenced points.
This work explores and demonstrates conjunctive deep learning of vehicle dynamics in compound feature vector spaces for intelligent dead-reckoning navigation. Our experiments show promising improvements in the post-mission; however, after implementing and testing, we decided to move on to the pre-trained cases, in which the ANN is instructed using GIANT for training the AI/ML intelligent virtual aiding concept proposed here. What comes next is enhancing system performance in a greater range of real-time applications.
Besides air vehicles, the projected environment training can be extended to modern Navy and Marine Corps warfare, given the increased use of unmanned vessels. Further, shipboard inertial navigation systems suffer from the instantaneous random motions inherent in the marine environment, which add complexity to the system, including the difference between actual dynamics sensed by IMU and predicted dynamics that represent the un-modeled marine motions. The other aspect of this training is for dismounted warfighters, where different human motions/dynamics are simulated and used for training the AI/ML from which locomotion pattern can be determined.

Conclusions
Robustness to GPS jamming and spoofing is a long-sought goal in military applications, driving a history of alternative sensing techniques. This work demonstrates the effectiveness of virtual aiding methods to constrain and localize the search space in the state estimation task inherent in navigation processing, enabling better operability in GPS-denied conditions and environments. It is part of our effort to add robustness, intelligence and resiliency in high-risk scenarios such as GPS spoofing/jamming for air-land-sea operations.
The virtual measurement is a computational perception formed of a composition of sensor inputs that can see higher-dimensional features of the input space. This work explores the use of virtual sensing to see the environment in new ways and glean new signals for the purpose of navigation aiding and demonstrates conjunctive learning of vehicle dynamics in compound feature vector spaces for intelligent dead-reckoning.
Pre-programmed knowledge of vehicle dynamics can aid in the perception of features from limited observations. A supervised machine learning agent such as an ANN can be used to learn an improved forward function and capture additional domain knowledge of vehicle dynamics based on fusion of observable variables and optimally-estimated hidden ones. Integration of virtual aiding sensors is part of our effort to increase PNT resiliency. The system can support a flexible and scalable architecture for performing missions on a range of processors on any platform in any environment, with an emphasis on GPS-denied scenarios. The architecture is extensible to new sensor measurements and scalable to support real-time processing across a range of processor capabilities.
Acknowledgment
This article is based on material presented in a technical paper at ION GNSS+ 2021, available at ion.org/publications/order-publications.cfm.
Authors
Dr. Moafipoor is a Senior Navigation Architect and director of research and development, focusing on sensor-fusion architectures, application software, embedded firmware, and sensor interoperability in GPS and GPS-denied environments. Dr. Moafipoor holds a Ph.D. in Geodetic Science from The Ohio State University and has published over 50 peer-reviewed journal articles and conference papers.
Brad Despres is a Scientist, developing new techniques and algorithms for computational navigation, sensor compositing and fusion, physical dynamics state estimation and filtering. Mr. Despres holds a Master of Science in Computer Science, Computational Perception and Machine Learning from the Georgia Institute of Technology.
Bob Stadel serves as Vice President for AEVEX Aerospace, with over 25 years in then Defense & Aerospace Industry. He is a graduate of the Naval Nuclear Power Program and holds an MBA from the University of Utah.
Jim Fitch is an Aerospace Engineer at the LinQuest Corporation and is the Lead Systems Engineer for the GPS Interference and Navigation Tool (GIANT) model development and other projects involving space systems modeling and simulation. He received his master’s degree in Astronautical Engineering from the Air Force Institute of Technology, is a retired Air Force Officer who held such positions as Satellite Systems Engineer and Space Systems Analyst, and has over 30 years of experience in the industry.






