Cryptographic techniques can optimize the trade-off between authentication integrity (minimizing the probability of authenticating a modified message), ease of modification of existing signals (for operator and user acceptance), and minimal impact on existing users who will form the vast majority of the GNSS user population for some time to come.
A: A serious and growing concern for users of GPS and other GNSS constellations is the possibility that the pseudorandom code signals and navigation data encoded on them might be altered from what is originally transmitted by GNSS satellites. Instances of likely or potential GNSS spoofing have been reported multiple times in this magazine ([1]), as well as various approaches and tools for detection and mitigation ([2,3]), and concerns for specific user segments with the most demanding integrity requirements ([3]). The last two decades of research on spoofing and its mitigation have shown that, while most types of spoofing can be detected by existing receivers using a variety of monitor algorithms, it is difficult to guarantee detection of the most sophisticated forms of spoofing without new tools.
One useful technique likely to be provided to users in the future is the ability to authenticate their received GNSS signals. “Authentication” in this context means confirming that the received signals are the same as those transmitted by authorized sources (GNSS satellites) and have not been modified or overwhelmed by spoofers. Authentication can be limited to the navigation data encoded within the PRN code signal (see [4]) or include the spreading code signal as well.
Unlike indirect monitoring of the potential presence of spoofing, authentication represents a direct confirmation of the authenticity of received signals. To achieve this, some form of cryptography is required. This is a significant change because it implies modifying the interface between GNSS service provider and future users while not significantly affecting existing users who are not aware of this change and don’t need the benefits of authentication.
The basics of cryptographic authentication as it applies to GNSS signals are explained in [5, 6]. Unlike encryption, cryptographic authentication does not modify or obfuscate the transmitted data but instead adds a “signature” to it that is used later to verify the authenticity of the remainder of the data.
Authentication requires additional data bandwidth for these signatures, posing a significant challenge given the constrained data bandwidth of current signals and their pre-internet design. This article focuses on recent work ([7] and [8]) using multiple cryptographic techniques that consider the trade-off between authentication integrity strength and desired features (e.g., minimizing the probability of authenticating a modified message), feasibility of modification of existing signals (for operator and user acceptance), and limited impact on existing users who will form the vast majority of the GNSS user population for some time to come.
Watermarking
Existing civil GNSS signal authentication concepts, such as Chimera, incorporate the insertion of unpredictable “watermarks” of uninformative content into the GNSS spreading codes, which later allows authentication after the insertions are disclosed [9]. These watermarks are designed to have minimal effect on the spreading codes so that they can be inserted into existing signals without affecting legacy users who do not need signal authentication. Because this attempts to validate the spreading code as well as the encoded navigation data, receivers attempting to authenticate their signals must store raw radio frequency data containing the watermarked spreading codes. After the GNSS provider broadcasts these watermarked codes, the provider separately distributes a cryptographic “seed” so that receivers can generate replicas of the watermarks. Receivers can then go back and re-autocorrelate the spreading codes, considering the signal cryptographically authentic if the replica-to-raw autocorrelation increases correctly after incorporating the watermarks into the replicas [7].
There are several ways to generate watermarks from cryptographic seeds as part of this process, but it is essential to make implementation as data-efficient as possible for both the service provider and user while maintaining a high degree of authentication integrity. One approach based on Timed Efficient Stream Loss-tolerant Authentication (TESLA) was customized to support authentication of SBAS correction and integrity signals in [10] and can be expanded for use with all types of GNSS civil signals.
TESLA and ECDSA
Generating cryptographic seeds using TESLA is an alternative to the method known as (the) Elliptic Curve Digital Signature Algorithm, or ECDSA. With ECDSA, a provider produces a message and a signature for a receiver to use for immediate authentication. This signature is pseudorandom and thus can serve as the cryptographic seed of the watermarks. For ECDSA, this is done by asymmetrically providing a “public key” to all users and encoding the signature messages with a “private key” which is secret. The resulting signature can then be verified almost instantaneously by applying the public key. However, the signature messages that result tend to be very large relative to typical GNSS data rates of 50 to 500 bps, and the computation needed to perform authentication in real time is non-trivial [5].
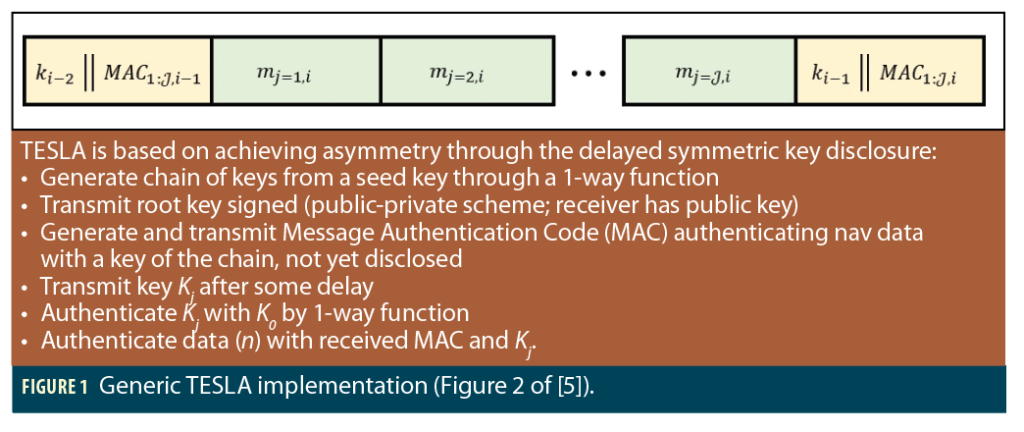
TESLA mitigates these problems by instead providing symmetric keys (the same keys at provider and user) that are provided soon after the signature messages that the keys are used to encode. This creates asymmetry in time: a key received at time t is used to authenticate a signature broadcast some time earlier (t – δt). Figure 1 (Figure 2 of [5]) illustrates the use of TESLA’s procedure to validate navigation data in terms of a time series of messages (m), keys (k, K), and Message Authentication Codes (MAC). The MACs represent message signatures and are verified using the same keys that generated (signed) them. First, the MAC is broadcast; then, the key is broadcast later. Both the MACs and the corresponding keys are needed to verify the message data, and since the keys are transmitted after some delay, verification of each set of messages is delayed until the key is provided. The security of authentication arises from how only the original message provider could have generated the message with the transmitted MAC signature before the release of the key [5].
TESLA-based Message Authentication
Authentication of the spreading codes is more complex than authentication of encoded data. Since the spreading codes in GNSS ranging signals exist below the thermal noise floor, receivers must know and therefore be able to generate local replicas of the spreading code to deduce pseudoranges. Cryptographic pseudorandom information added to the spreading code must be delivered to receivers separately from the spreading code itself. The advantage of ECDSA in non-GNSS contexts (e.g., internet authentication) is that the receiver can authenticate information immediately, as opposed to the required delay for a so-called “bit-commitment” scheme such as TESLA. However, since the nature of GNSS (the need for correlation of received signals to local replicas) invalidates this feature of ECDSA, it would be better to use a method based on TESLA to exploit the additional features provided by bit-commitment schemes [7].
TESLA provides several advantages relevant to GNSS over exclusively using ECDSA.
First, a small cryptographic distribution can authenticate unlimited information, alleviating the constraint posed by limited GNSS message bandwidth. Second, if a receiver misses a cryptographic distribution, a receiver can rederive that distribution from a later distribution, providing loss tolerance. Third, the cryptographic functions used can be more computationally efficient, saving receiver computation and power. Further, TESLA is used in tandem with ECDSA rather than completely replacing it. ECDSA’s use within TESLA effectively acts as the rekeying operation for TESLA.
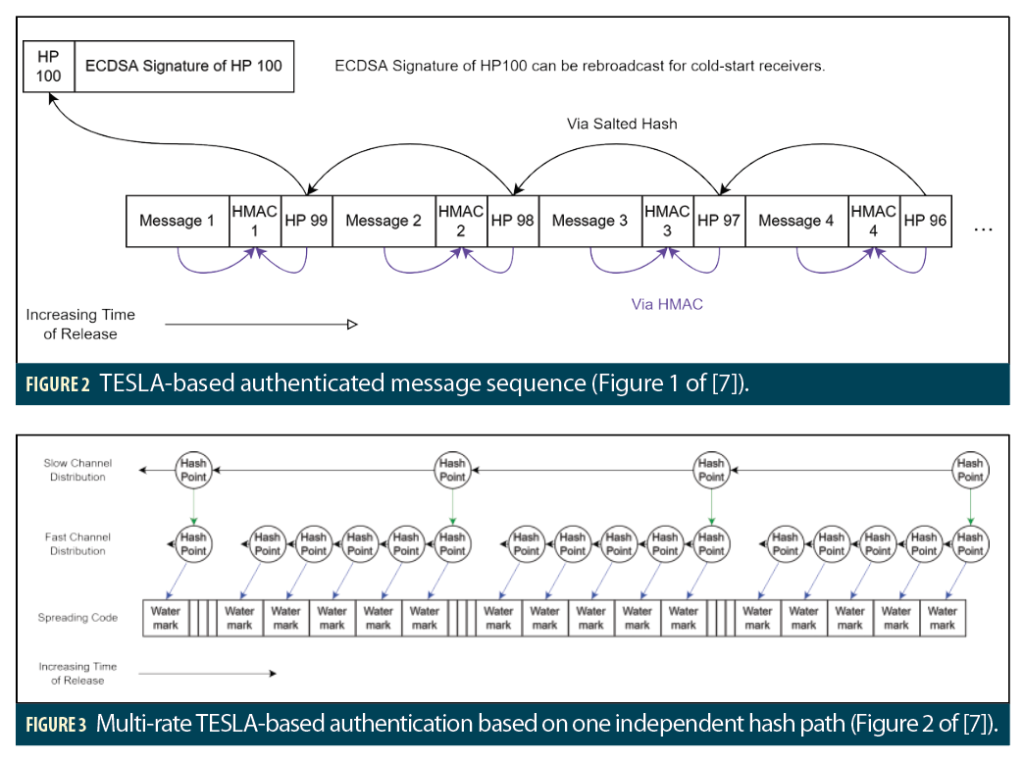
TESLA requires the construction of a one-way set of n-bit integers related via repeated application of a cryptographic hash function, where n is the security level of the protocol. Each n-bit integer among the set serves as a hash message authentication code (HMAC) key at a particular time agreed to by provider and receiver [11]. Each n-bit integer is called a Hash Point, and a collection of Hash Points consecutively related via the Hash Function is called a Hash Path. Non-consecutive Hash Points further along the Hash Path are connected via repeated application of the Hash Function. The first Hash Point along the path is called the Hash Path Start, which is just a random n-bit integer. The last Hash Point along the path is called the Hash Path End. The Hash Function (e.g., SHA-256—see [11]) is secure in that it is trivially easy to compute the final Hash Point of the Hash Function given the initial Hash Point, but one can only use exhaustive search to find any initial Hash Point. In other words, the Hash Path is a one-way path. The domain of n-bit integers, together with a randomized n-bit “salt” inclusion to the Hash Function and n ≥ 128, make external precomputation attacks (also called Rainbow Table Attacks) infeasible with modern supercomputers. To complete the security framework, the Hash Path End is separately signed with the ECDSA procedure [7].
Figure 2 (Figure 1 of [7])shows a simple stream of messages authenticated with TESLA. In this figure, the message provider first generates a complete Hash Path and holds the entire Hash Path secret except for the Hash Path End. In Figure 2, the length of the path is 100 Hash Points (HPs). Second, the provider uses ECDSA to sign the Hash Path End (HP 100) and distributes the Hash Path End with an ECDSA signature. Third, the provider sends a message (Message 1 in Figure 2) with an HMAC derived from both that message and the currently-secret “preimage” of the Hash Path End, meaning the immediately preceding HP in the Hash Path (i.e., HP 99). Fourth, the provider sends the actual preimage of the Hash Path End (HP 99), meaning it is no longer secret. Fifth, the provider returns to the third step to send a new message (Message 2) and HMAC with the secret second preimage of the Hash Path End (HP 98). This repeats until the provider runs out of preimage Hash Points, at which point it must return to the first step and regenerate a new Hash Path. The receiver’s procedure for validating this received message path is described in detail in [7].
Multi-Rate Message Authentication
Reference [7] describes an intricate procedure for extending the TESLA-based message authentication procedure to spreading-code authentication based on the generation of separate “slow” and “fast” Hash Paths from a single TESLA sequence to minimize the degradation in spreading code performance created by the insertion of watermarks for authentication (this degradation would be greater if separate Hash Paths were generated independently). This approach takes advantage of the scalability of the TESLA approach since a fixed distribution of TESLA Hash Points can authenticate any amount of information transmitted prior to the Hash Point distribution (within user computation constraints).
Figure 3 (Figure 2 of [7]) shows an overview of this procedure and illustrates the derivation of higher-rate Hash Paths from slower ones by “forking,” as defined mathematically in Section II of [7]. Each black arrow in this figure represents a “normal” hash operation as described previously. The Slow Channel (Hash Path) at the top of the figure is generated first, and the Fast Channel is created from periodic forks (green arrows) of the Slow Channel (via equations (3) and (4) of [7]) combined with normal hash operations in between Slow-Channel updates. Each HP in the Fast Channel is then forked (via equations (7) and (8) of [7]) to generate the watermarks introduced into the spreading-code signal.
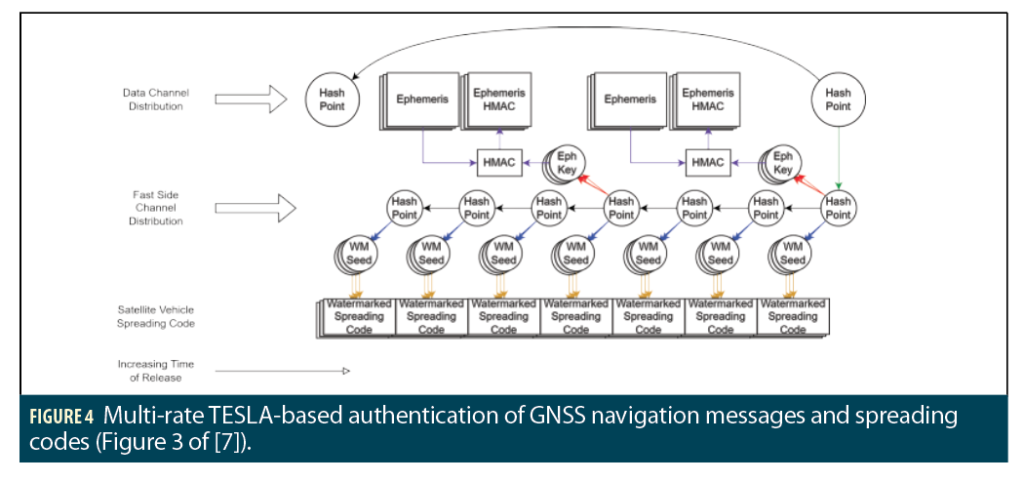
Figure 4 (Figure 3 of [7]) shows how the procedure of Figure 3 is further extended to the authentication of both code and data components of GNSS signals. In Figure 4, “Ephemeris” refers to the navigation data messages encoded within these signals that supplies satellite ephemeris information, clock corrections, satellite health, and other information. It is authenticated using “Eph Keys” generated from the Fast Channel (red and purple arrows, which correspond to equation (5) of [7] and the normal hashing process of [11]). The watermarks inserted into the spreading code are created by a two-step process from the Fast Channel (blue arrows corresponding to equation (7) of [7]) and yellow arrows corresponding to the “watermarking function” derived in Section V of [7]. With this procedure, we can authenticate all GNSS navigation message data and spreading codes with a minimal distribution and better utilize the limited GNSS data bandwidth.
The (Near) Future of GNSS Authentication
This article and the details in [7] describe one approach to combined navigation message and spreading code authentication. However, the complexity of this and similar approaches and the need to modify both service provider/satellite transmission protocols and receiver algorithms for users who desire authentication suggests that both code and data GNSS authentication capability will not be in operation before the end of this decade. However, important steps toward this goal are already being made, starting with the easier task of authenticating navigation data messages.
Recently, the European Union Agency for the Space Programme (EUSPA) has published an Info Note and technical details regarding a test phase for Galileo Open Service Navigation Message Authentication (OSNMA) [12, 13]. OSNMA uses a variant of TESLA to distribute cryptographic signatures authenticating Galileo Open Service navigation data messages. These signatures will be broadcast in previously reserved segments of the Galileo navigation message definition (so as not to create a demand for additional bandwidth) from a subset of Galileo satellites. Cross-authentication allows OSNMA to verify navigation data messages from all satellites using only signatures from a subset of the satellites [13].
Authentication of the 250-bit correction and integrity messages encoded on Satellite-based Augmentation System (SBAS) signals is also an area of active development. Reference [10] defines a combined TESLA-ECDSA technique for this that is related to the multi-rate procedure for combined code and data authentication described here and in [7]. Message authentication will help maintain confidence that SBAS continues to meet the demanding integrity requirements that apply to aviation applications of SBAS, such as precision approach under low-visibility conditions.
Summary
GNSS signal authentication is expected to be integrated within GNSS services in the next decade or two. One approach to combined authentication of both GNSS navigation data and spreading codes is presented, and its advantages relative to other standard techniques are discussed. Making authentication feasible for future users who require or desire it requires significant changes to both service provider and user equipment and procedures. This emphasizes the need to select authentication approaches that provide the required message verification without undue signal modification, receiver complexity, or undesired effects on the bulk of existing users who will continue to operate without this feature.
References
(1) “Sinister Spoofing in Shanghai,” Inside GNSS, December 10, 2019.
(2) G.W. Hein, “Real World Spoofing Trials and Mitigation,” Inside GNSS, May 27, 2017.
(3) “DHS Publishes Free Resources to Protect Critical Infrastructure from GPS Spoofing,” Inside GNSS. March 5, 2021.
(4) “What is navigation message authentication?,” Inside GNSS, January 1, 2018.
(5) A. Neish and T. Walter, “Securing GNSS—A Trip Down Cryptography Lane,” Inside GNSS, May 20, 2020.
(6) “From Data Schemes to Supersonic Codes,” Inside GNSS, January 16, 2015.
(7) J. Anderson, S. Lo, T. Walter, “Efficient and Secure Use of Cryptography for Watermarked Signal Authentication,” Proceedings of ION ITM 2022, Long Beach, CA, January 25-27, 2022 (forthcoming).
(8) J. Anderson, S. Lo, T. Walter, “Cryptographic Ranging Authentication with TESLA, Rapid Re-keying, and a PRF,” Proceedings of ION ITM 2022, Long Beach, CA, January 25-27, 2022 (forthcoming).
(9) J. M. Anderson, K. L. Carroll, N. P. DeVilbiss, et al, “Chips-Message Robust Authentication (Chimera) for GPS Civilian Signals,” Proceedings of ION GNSS+ 2017, Portland, OR, September 25-29, 2017, pp. 2388–2416.
(10) J. Anderson, S. Lo, A. Neish, T. Walter, “On SBAS Authentication with Over-the-Air Re-keying (OTAR) Schemes,” Proceedings of ION GNSS+ 2021. St. Louis, MO, Sept. 20-24, 2021, pp. 4288-4304.
(11) “HMAC,” Wikipedia. https://en.wikipedia.org/wiki/HMAC. Accessed January 11th, 2022.
(12) “Info Note Available for Galileo Message Authentication (OSNMA); Public Observation Now Underway,” Inside GNSS. December 29, 2021.
(13) Galileo Open Service Navigation Message Authentication (OSNMA): Info Note, EUSPA, December 2021. doi:10.2878/49446. https://www.gsc-europa.eu/sites/default/files/sites/all/files/Galileo_OSNMA_Info_Note.pdf.