Performance evaluation of PPP correction services for Galileo HAS and QZSS MADOCA-PPP.
VICTOR CLAMADIEU, JULIE ANTIC, PEDRO ROLDAN, SÉBASTIEN TRILLES, THALES ALENIA SPACE
Global Navigation Satellite Systems (GNSS) have revolutionized our ability to determine accurate position. Today, many applications that cover the mass market, professional and safety-critical applications rely heavily on GNSS technology for Position, Navigation and Timing (PNT) and many of these applications raise the need for greater accuracy.
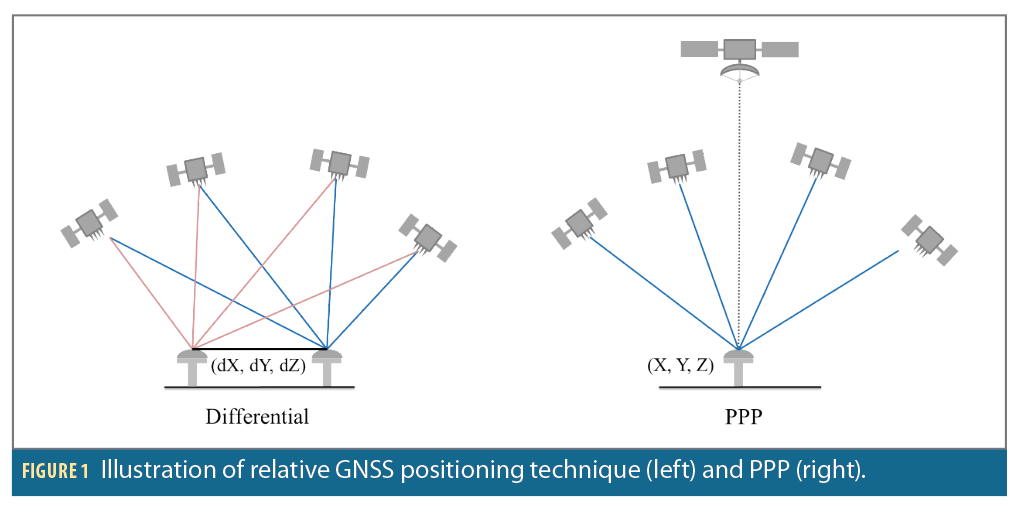
For three decades, relative (or differential) positioning has been the dominant precise positioning and data processing technique. In relative positioning, the coordinates of a point are determined relative to another reference point with known coordinates. This eliminates or reduces most GNSS observation errors that are spatially correlated at both the unknown and reference points, thus providing high accuracy positioning solutions.
Originally, the implementation of this relative positioning technique involved one reference station and one or more rover receivers operating in a local area, in real-time. Submeter to centimeter-level positioning accuracy can be obtained, with the accuracy mainly dependent on whether the pseudorange or/and carrier phase observations are used, and in the latter case, whether ambiguity resolution was successful.
Carrier phase processing provides the most accurate positioning results, in real-time and in dynamic mode, in a technique known as Real-Time Kinematic (RTK). RTK is now, and has been for many years, the industry standard procedure for precise positioning and navigation applications such as machine control, precision farming, surveying and mapping. This technique was soon augmented to a regional network of reference stations that permitted the extension of the service coverage area in the so-called “network-RTK” mode. In this case, we speak of an Observation State Representation (OSR), for which a single term corresponding to the sum of the corrections applied to the observations is transmitted to users.
Precise Point Positioning (PPP) is an approach to satellite-based navigation that promises high-accuracy positioning data. The interest in PPP is manifold and largely owed to the fact it enables users to obtain a greater degree of accuracy than traditional GNSS-only solutions. In contrast to relative positioning techniques, PPP provides absolute positioning without the need for a reference or base station, which makes it extremely valuable for global operations in areas where local infrastructure might be lacking or non-existent.
The PPP approach consists of modeling or estimating each term composing the phase measurements rather than trying to eliminate them. In this case, we speak of State Space Representation (SSR). Indeed, because the unmodeled signals cannot be easily eliminated in PPP, which is based on undifferenced observations, the errors linked to the satellite system, the receiver and the physical nature of the Earth such as atmospheric effects must be either properly corrected or modeled. While some of these errors can be modeled and corrected at the user-level via correction models, “external” corrections such as satellite orbits, clocks and hardware bias are required for transmission to users. PPP has several benefits:
1. Global applicability: PPP can be used anywhere in the world because it doesn’t require a base station at a known position close to the user, whereas RTK/network-RTK needs a dense local/regional GNSS infrastructure.
2. Around-the-clock accessibility: Unlike differential GPS-based methods, which can be affected by reference station availability, PPP is available 24/7, given satellite signal availability.
3. High accuracy: PPP provides high accuracy on the order of a few centimeters with proper signal corrections.
Today, PPP faces important challenges, like:
1. Accuracy of orbit, clock and hardware bias products: Because PPP is highly affected by GNSS satellite orbit and clock errors, but also by code bias for uncombined formulation and phase bias for the integer ambiguity resolution (IAR), availability of accurate products is a must-have for PPP.
2. Convergence time: PPP requires a convergence period for the estimation of the carrier phase ambiguity. In relative positioning, the ambiguity can be fixed instantaneously thanks to the cancelling of hardware-dependent bias with double-differences. The provision of precise atmospheric corrections (ionospheric and tropospheric) is a potential solution for reducing PPP convergence time.
3. Local error modeling and mitigation: Dealing with all error sources, including local errors, is a challenge for users who can move from urban canyons to open sky.
4. Infrastructure and data handling: With the new generations of GNSS services, satellites are increasing in number, leading to more corrections data to handle and more complex algorithms for the positioning process.
5. Integration with other technologies: Fusing PPP with other technologies such as inertial navigation systems (INS) or LiDAR is still a challenge but could lead to more robust and versatile positioning solutions in the future.
6. Integrity: PPP’s reliability and integrity, prerequisites for safety of life applications such as autonomous transportation, represent areas of intensive research.
The primary ambition of the PPP correction services studied in this article is to tackle the first challenge by leveraging accurate orbit and clock corrections. Subsequently, they aim to address the second challenge by broadcasting precise atmospheric corrections.
Precise satellite orbit and clock corrections have long been supplied by commercial providers for PPP. However, in recent years, the GNSS systems themselves have started to broadcast these types of corrections in real time, for free.
Trailblazing the way, BeiDou Global Navigation Satellite System (BDS-3) has been providing an initial real-time PPP service since 2020 over the Asia Pacific region [1].
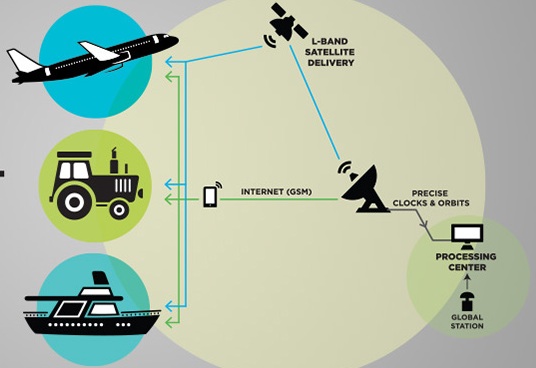
Available since September 2022, the Multi-GNSS Advanced Orbit and Clock Augmentation – Precise Point Positioning (MADOCA-PPP) trial service broadcasts accurate corrections for GPS, Galileo, BeiDou and GLONASS through the Quasi Zenith Satellite System (QZSS) Signal In Space (SIS) over the East Asia and Pacific region and worldwide via the internet. The QZSS MADOCA orbit and clock corrections are meant for regional PPP service over East Asia and the Pacific region.
Since January 2023, the initial Galileo High Accuracy Service (HAS) has been declared operational and broadcasts corrections for GPS and Galileo worldwide through Galileo SIS and the HAS Internet Data Distribution (IDD) service [2].
The emergence of these services has sparked an increased interest in assessing their performance, and there have been important forays into this investigation.
For BDS-3 PPP, [3] evaluates the long-term performance of the service for time applications.
For MADOCA-PPP, [4] and [5] document the range and positioning performances for real-time PPP and PPP with ambiguity resolution.
For Galileo HAS, even before its operational phase, the architecture, products and performances of initial service has been revealed in [6] and [7]. Since the operational phase, [8] provides quarterly report of range performances, [9] assesses range and positioning performances in an urban driving environment and [10] reports the positioning performances from all the International GNSS Service Multi-GNSS Experiment stations over the world.
This article presents the performance of these new services and the generic and flexible tools, Orbits and Clocks Explorer and Analyser (OCEAN) and High Accuracy Positioning in PYthon (HAPPY) that leverage the latest generation technologies. The study has been limited to Galileo HAS and MADOCA-PPP, available worldwide through SIS for Galileo HAS and the internet for MADOCA PPP. The BDS-3 PPP coverage area is limited to the Asia Pacific region.
PPP Correction Services Overview
QZSS MADOCA-PPP
MADOCA-PPP is an open access and free QZSS service that provides precise corrections transmitted in the QZSS L6 signal from QZSS satellites as well as via the internet.
QZSS MADOCA-PPP will provide two correction services:
• High accuracy corrections (orbits and clocks) for Galileo I/NAV and GPS, GLONASS and QZSS L/NAV navigation messages, and biases (code and phase) for Galileo E1 and E5a signals and for GPS, GLONASS and QZSS L1, L2 and L5 signals.
• Ionospheric corrections available in the Asia and Pacific regions.
Currently, global corrections are in trial service and will be operational in 2024. Ionospheric corrections will be in trial service in 2024.
The QZSS MADOCA-PPP architecture is as follows:
• GNSS data are received by monitoring station and collected by the Multi-GNSS Integrated Real Time and Archived Information system (MIRAI);
• High accuracy corrections are computed by control stations;
• These corrections are transmitted to users via the internet or by QZSS satellites.
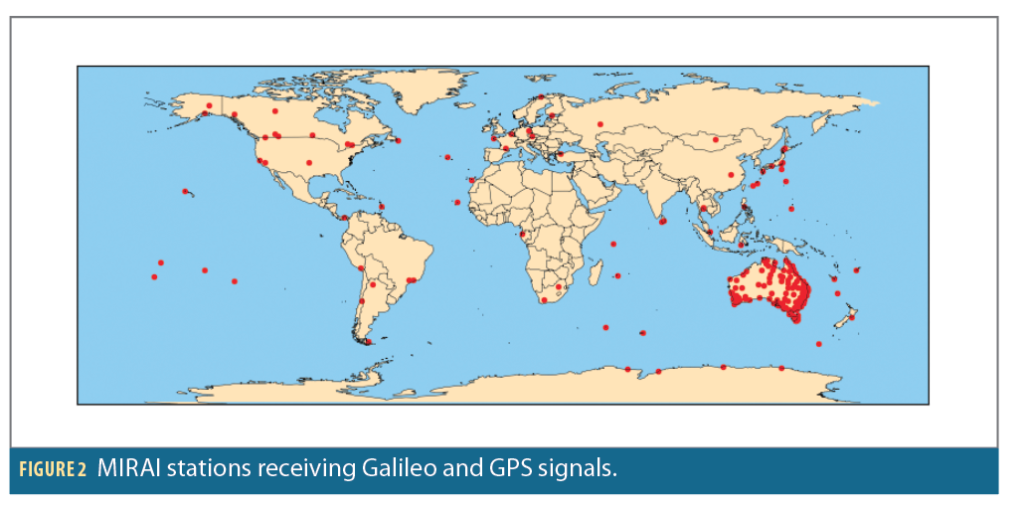
The MIRAI network consists of a large number of stations distributed all over the world, with an increased density over Asia and Oceania.
Table 1 details the validity and refresh time of QZSS MADOCA-PPP corrections.


Galileo HAS
HAS is an open access and free Galileo service that provides precise corrections transmitted in the Galileo E6 signal from a subset of Galileo satellites, as well as via the internet.
The Galileo HAS full service, available in 2024, will provide two service levels:
• The Service Level 1 (SL1), with global coverage, providing high accuracy corrections (orbits and clocks) for Galileo I/NAV and GPS L/NAV navigation messages, and biases (code and phase) for Galileo E1, E5a, E5b, E6 and E5AltBOC and GPS L1, L2 and L5 signals;
• The SL2, with regional coverage (European coverage area), providing SL1 corrections and atmospheric corrections.
Currently, the Galileo HAS initial service is available and provides SL1 without phase biases.
The Galileo HAS architecture is as follows:
• Galileo and GPS are received by the Galileo Sensor Stations (GSS) and transmitted to the High Accuracy Data Generator (HADG);
• The HADG computes corrections;
• These corrections are transmitted to users via the internet or by Galileo satellites connected to Up-Link Stations (ULS).
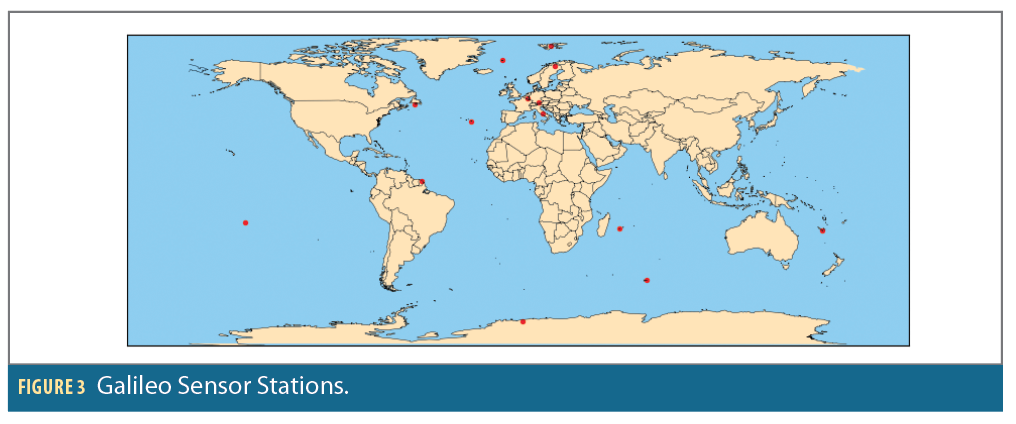
Figure 3 shows the GNSS stations that provided the data used to compute PPP corrections at the time of the test. An additional station was deployed in Wallis in May 2023.
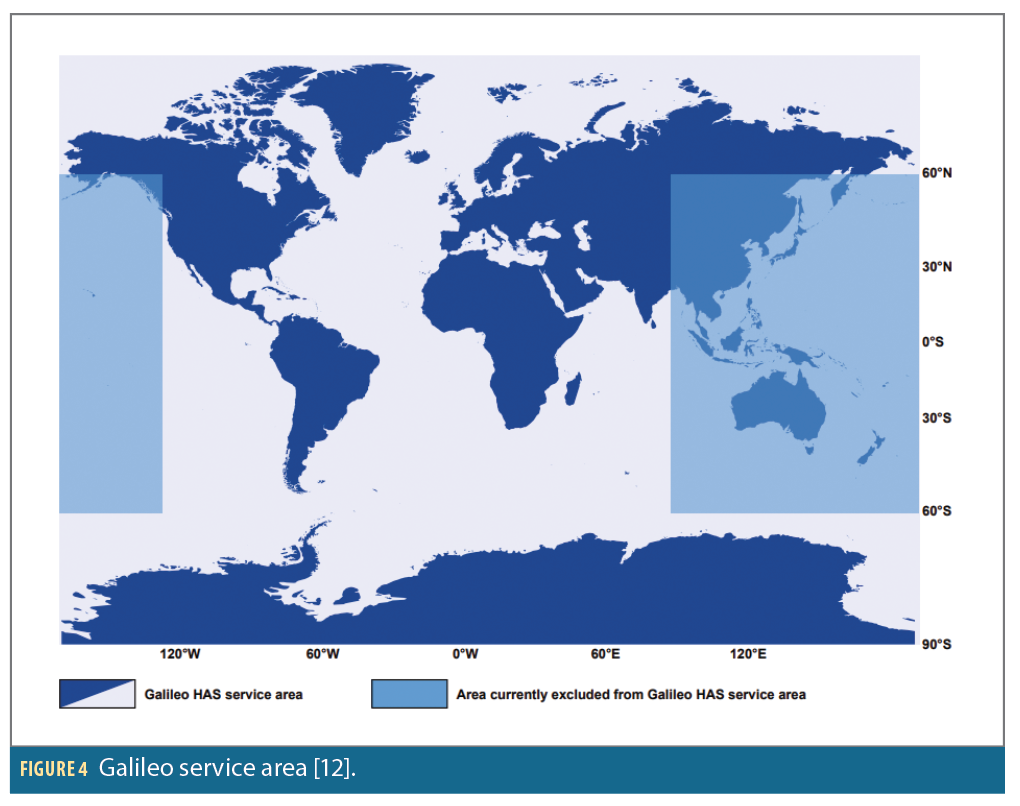
As detailed in [11], HAS service commits to a positioning performance of less than 20 cm@95% in horizontal direction and less than 40 cm@95% in vertical direction, all around the world except on the Asia Pacific region, as illustrated in Figure 4, because of a lack of monitoring stations in this area.
Table 2 details the validity and refresh time of Galileo HAS corrections.
SSR Corrections
As shown in Tables 1 and 2, each correction has its own validity time and refresh time, which are defined by the systems that provide them.
Orbit Corrections
Orbit corrections are provided in the Satellite Coordinate System (SCS) NTW composed of the radial (εn), in-track (εt) and cross-track (εw) components and centered in the satellite’s ionosphere-free antenna phase center.
These corrections apply to satellite positions calculated with broadcast navigation messages identified with IOD parameters. Each satellite position (xs) and speed (vs), in Earth Centered Earth Fixed (ECEF) frame, shall be computed using the algorithm described in the HAS SIS ICD [13] of the considered constellation.
The following steps describe how to compute corrected satellite positions:
• In-track unit vector:

• Cross-track unit vector:

• Radial unit vector:

• Correction vector in SCS NTW frame:

• Rotation matrix from SCS NTW to ECEF frame:

• Corrected satellite position:
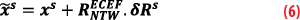
Clock Corrections
Clock corrections δC (expressed in meter) are delta offsets to be added to the ionosphere-free satellite clock computed from the broadcast navigation messages identified with IOD parameters.
Each ionosphere-free satellite clock dts shall be computed using clock second order polynomial coefficients (af0,af1,af2) as described in the HAS SIS ICD [12] of the considered constellation, but excluding the relativistic correction term (this term shall be computed and added separately).
The following steps describe how to compute corrected satellite clock:
• Relativist correction:

• Corrected satellite clock:

Code Biases
Code bias dbjs provide the offset to be applied to the individual signals j targeted by each bias.
For each satellite, the corrected pseudorange is computed as follows:

Therefore, code biases replace Broadcast Group Delays (BGDs) and Timing Group Delays (TGD) provided by navigation messages.
So, they are the biases to switch from the ionosphere-free clock provided by SSR message to the single frequency clock associated with the signal j.
Methods
A look at the Key Performance Indicators (KPIs) evaluated for each service of PPP corrections.
Data Processing
GPS and Galileo navigation messages are taken from Receiver Independent Exchange (RINEX) navigation files available on the internet and provided by International GNSS Service (IGS) [13].
QZSS MADOCA-PPP data are extracted from data received on the L6 band and available on the internet [14].
Galileo HAS data are extracted from the data received on the E6 band by a receiver on Thales Alenia Space premises in Toulouse.
Final products of the Center for Orbit Determination in Europe (CODE) are used to evaluate performance at system level (orbit, clock and code bias accuracy) and at user level (position accuracy) [15]. The reference orbits from CODE are transferred from center of mass to center of phase thanks to the phase center offsets provided in the IGS ANTEX file. The reference clocks from CODE are transferred to the HAS reference thanks to inter-frequency biases (SINEX BIAS files) and removing a common clock offset by constellation.
Performance at System Level
Performance at system level is evaluated throughout April, with a time step of 5 seconds. It is described by the following KPIs:
• Availability
• Orbit accuracy
• Clock accuracy
• Code bias accuracy
These KPIs are computed using the Thales Alenia Space OCEAN tool.
Availability
Availability is defined as the percentage of time that all corrections (orbit, clock and code bias) are available. This value is normalized by the percentage of time that a navigation message is available.

Where:
ncorr is the number of time with an available set of corrections
nnav is the number of time with an available navigation message
Orbit Accuracy
Orbit error is defined as the range between the corrected satellite position and the reference satellite position
.

Orbit accuracy is evaluated as the 95 percentile of the orbit error for each satellite.
Clock Accuracy
Clock error is defined as the difference between the corrected satellite clock and the reference satellite clock
minus the average clock error over the constellation C containing nC healthy satellites.
The reference satellite clock is extracted from SP3 with respect to E1-E5a for Galileo and L1P(Y)-L2P(Y) for GPS then transferred to L1C/A-L2P(Y) using reference code bias extracted from SINEX-BIAS.

The term ∆ allows us to compare the clock with respect to the same reference. It is computed as the ionosphere-free combination of the HAS code bias associated to E1 and E5a frequencies for Galileo and L1C/A and L2P(Y) frequencies for GPS:

where γ1,2 stands for the square of frequencies ratio
The term is an estimate of the unobservable time offset between the constellation and reference data.
Clock accuracy is evaluated as the 95 percentile of the clock error for each satellite.
Code Bias Accuracy
Code bias error is defined as the difference between the satellite code bias and the reference satellite code bias
, minus the average code bias error over the constellation.
The reference code bias is the bias to switch from the reference combination provided by the SSR message to single frequency clock associated with the signal j and is computed with SINEX-BIAS data.
For each signal and constellation, the code bias accuracy is evaluated as the 95 percentile over the constellation’s satellites of the code bias errors’ root mean square.
Performance at User Level
Performances at user level is evaluated on IGS stations over one day (April 1, 2023) with a time step of 5 minutes. We chose to use fixed stations so local errors would not outweigh system errors within the coverage area of each system:
• MIZU in Japan for QZSS MADOCA-PPP
• GRAC in France for Galileo HAS
The positioning performance evaluation is performed with the Thales Alenia Space tool HAPPY, which uses a PPP algorithm based on an Extended Kalman Filter (EKF) and offers a high degree of configurability with respect to pseudo-range combination, ambiguity resolution, Kalman states, the modeling of delays, bias and random errors. We chose the following configuration for this study:
• Dual frequency uncombined measurements (E1-E5a for Galileo and L1C/A L2P(Y) for GPS)
• Float ambiguity, so satellite-satellite Single Differences (SD) are disabled to avoid increasing measurement noise
• Cycle slip detection and correction
• Receiver Autonomous Integrity Monitoring (RAIM) algorithm for Fault Detection and Exclusion (FDE)
Results
QZSS MADOCA-PPP
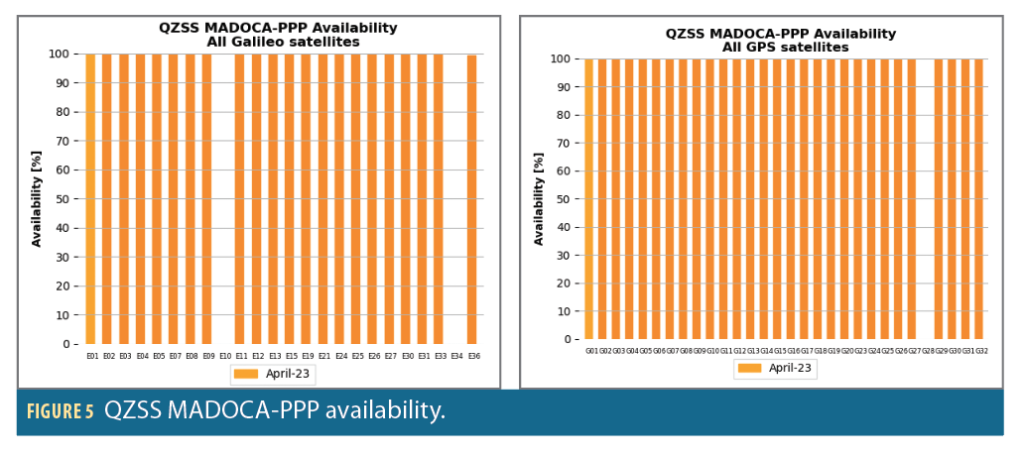
As detailed in Figure 5, the availability of MADOCA-PPP correction is very good on the studied month: 100% for all GPS and Galileo satellites, except for three fully unavailable satellites (E10, E34 and G28).
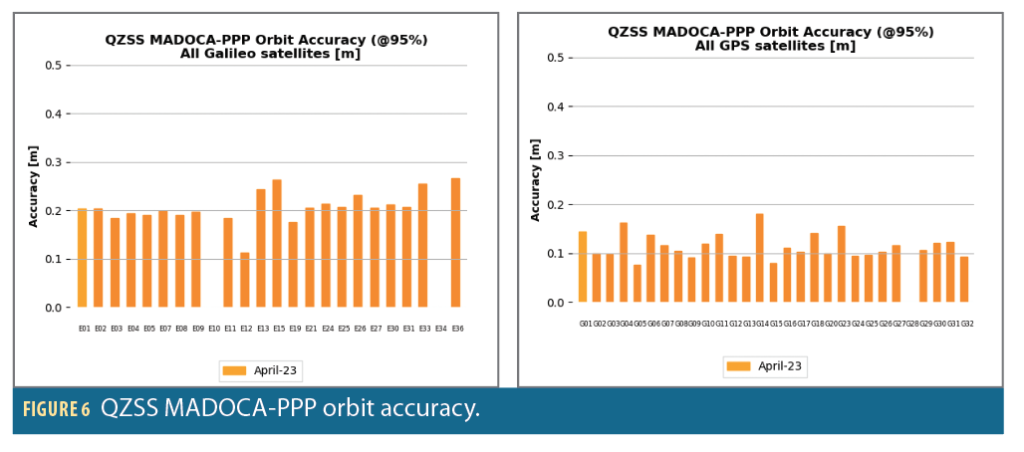
As illustrated in Figure 6, the orbit correction accuracy of MADOCA PPP corrections at 95% is about 20 centimeters for Galileo and 10 centimeters for GPS, providing a huge improvement with respect to Open Service (OS), with orbit accuracy in the meter range.
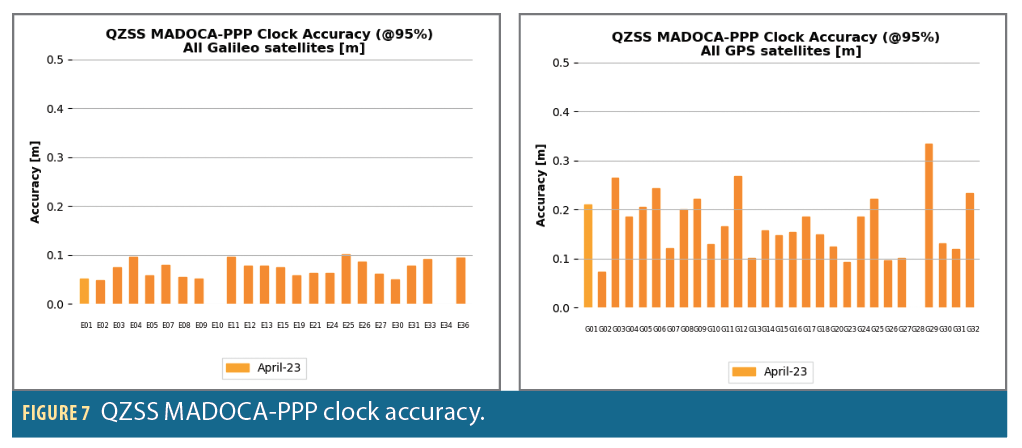
Concerning clock accuracy (Figure 7), QZSS MADOCA-PPP achieves excellent performances: An accuracy at 95% of 15 centimeters for GPS, and 5 centimeters for Galileo, taking advantage of the high update rate of clock corrections (5 seconds) and Galileo clocks stability.
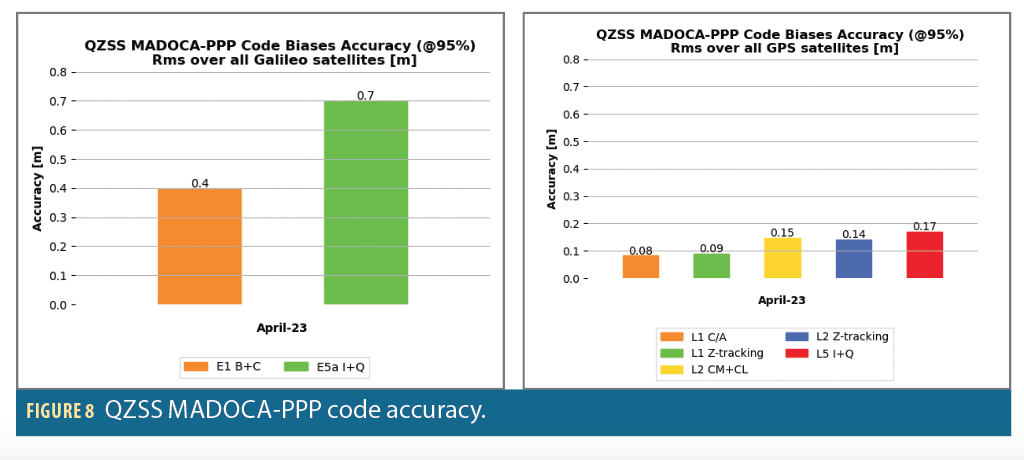
QZSS MADOCA-PPP code bias correction accuracy at 95% is between 8 and 17 centimeters for GPS, and 40 and 70 centimeters for Galileo.
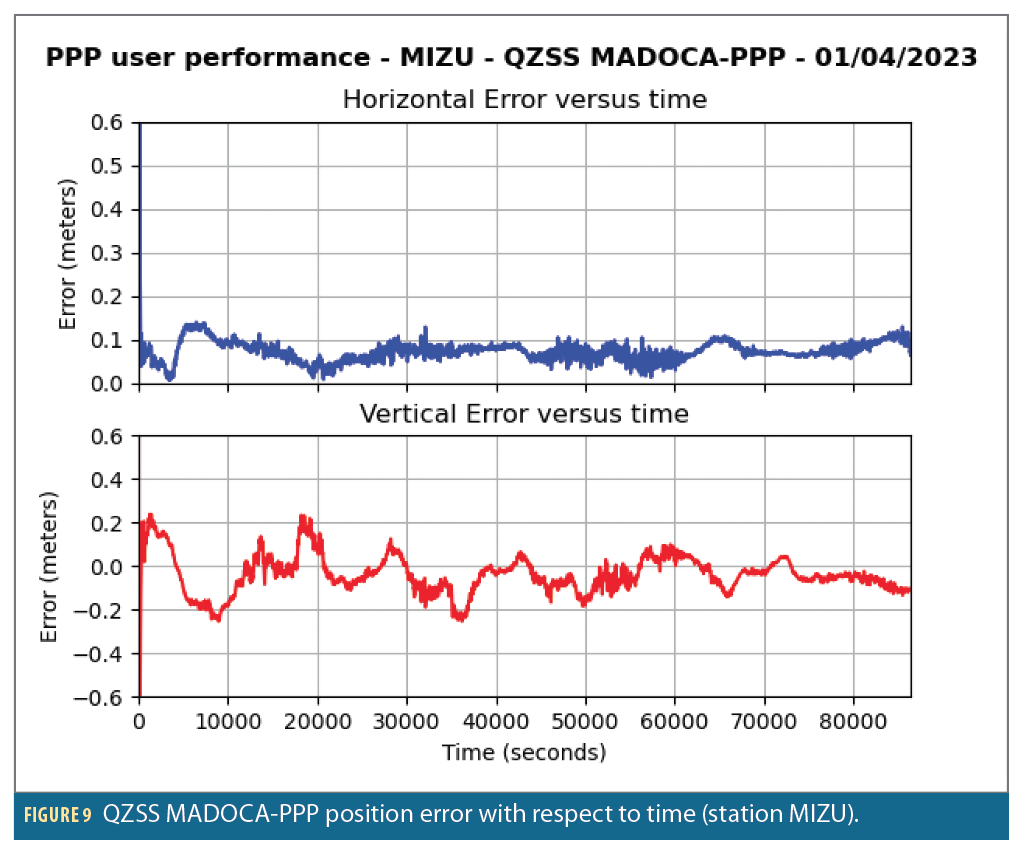
At user level on MIZU station (in Japan), QZSS MADOCA-PPP corrections reach decimeter-level accuracy in a few minutes.
Galileo HAS
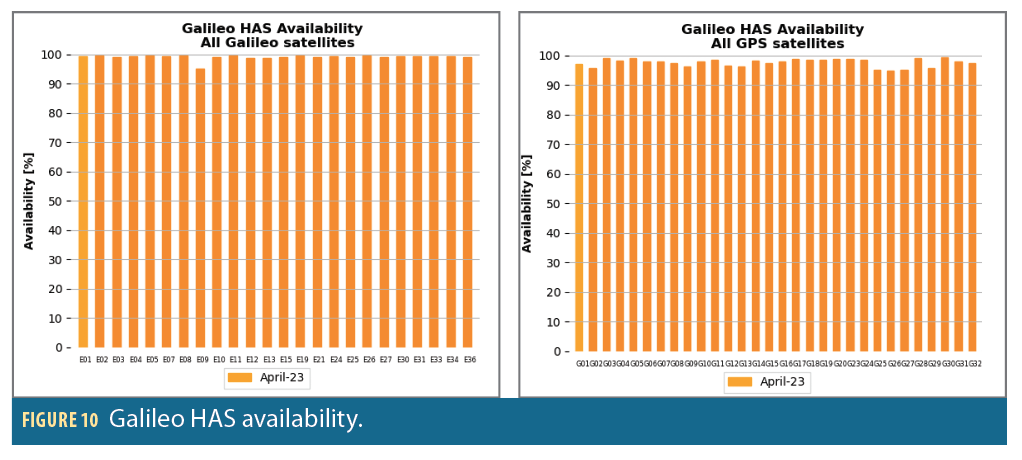
As shown in Figure 10, the availability of Galileo HAS is very good on the studied month with more than 95% for all GPS and Galileo satellites.
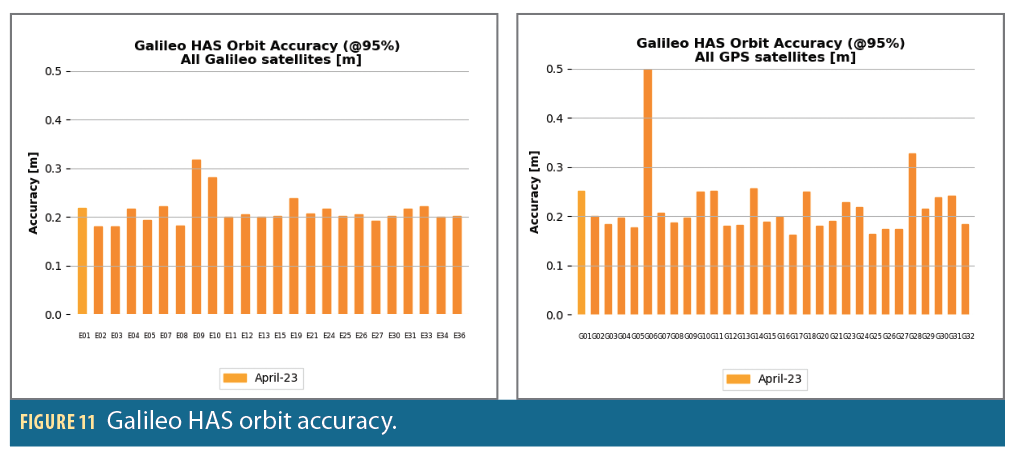
As detailed in Figure 11, the Galileo HAS orbit error accuracy at 95% is about 20 cm for Galileo and GPS satellites. More precisely, the instantaneous constellation RMS equals 17 cm for Galileo and 21 cm for GPS in compliance with the minimum performance levels from [11] that are 20 cm for Galileo and 33 cm for GPS.
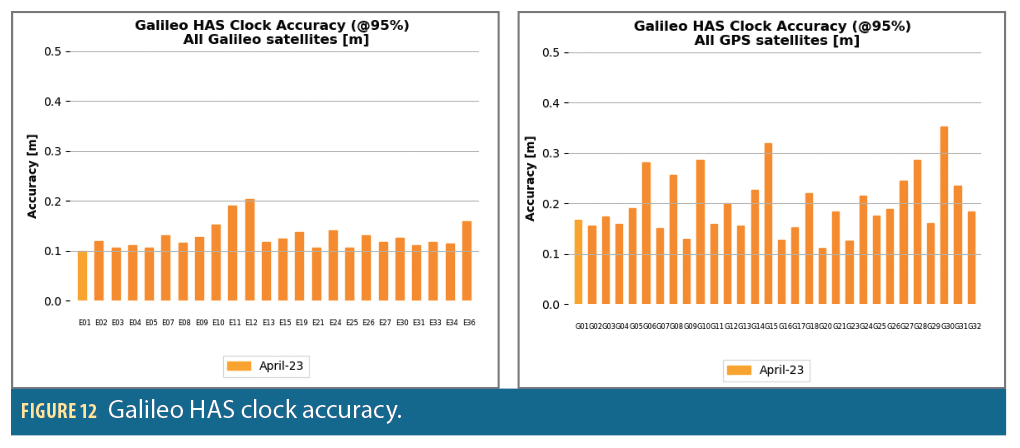
As detailed in Figure 12, the Galileo HAS clock error accuracy at 95% is about 10 cm for Galileo and 20 cm for GPS satellites. The instantaneous constellation RMS equals 9 cm for Galileo and 15 cm for GPS, fully compliant with the minimum performance levels from [11]: 12 cm for Galileo and 15 cm for GPS.
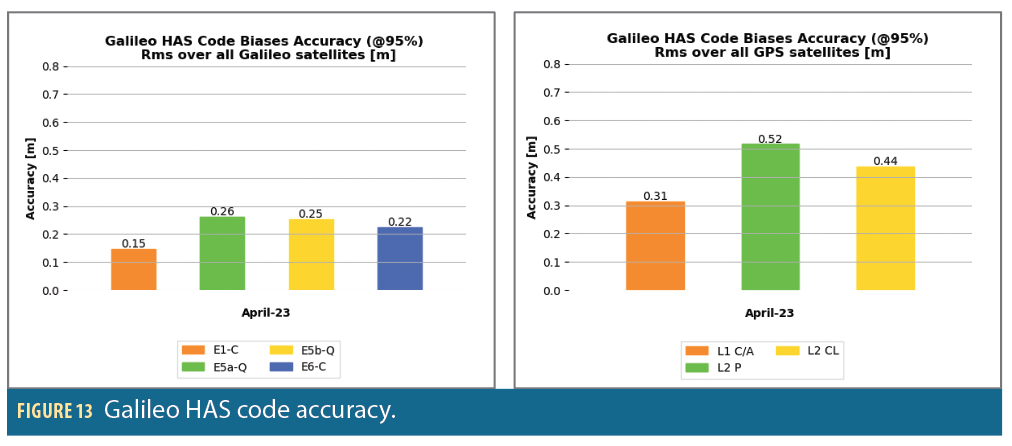
As detailed in Figure 13, the RMS of the Galileo HAS code bias accuracy at 95% is fully compliant with the minimum performance levels from [11]: 50 cm for Galileo and GPS constellations.
At user level on the GRAC station in France, Galileo HAS corrections permits decimeter-level accuracy in a few minutes.
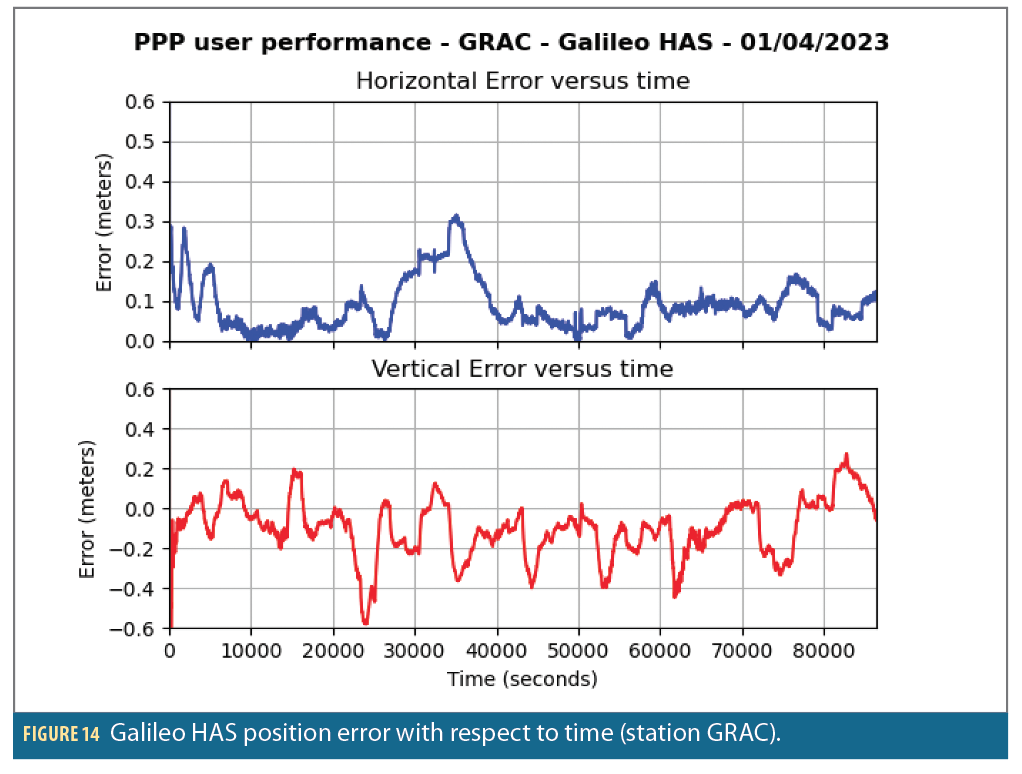


Conclusion
The performance evaluation of Galileo HAS and QZSS MADOCA-PPP correction services has been reached with new flexible and versatile tools, OCEAN and HAPPY.
Using these tools, it appears the accuracy of QZSS MADOCA-PPP and Galileo HAS corrections significantly surpass the OS accuracy for orbit, clock and bias, reducing it from the meter to the centimeter range in RMS for GPS and Galileo.
At the user level on a fixed station, they enable attainment of decimeter-level accuracy.
Looking ahead, there are numerous exciting opportunities for additional studies. In a few months, the deployment of higher service levels for Galileo HAS and MADOCA will permit access to the benefits of phase bias and atmospheric corrections for PPP convergence time reduction and integer ambiguity resolution, which could be a game changer for precise positioning.
References
(1) http://www.beidou.gov.cn/xt/gfxz/202008/P020200803362062482940.pdf.
(2) EUSPA (2023). Galileo High Accuracy Service goes Live! EU Agency for the Space Programme. https://www.euspa.europa.eu/newsroom/news/galileo-high-accuracy-service-now-operational.
(3) He, Q., Chen, L., Liu, L., Zhao, D., Gong, X., Lou, Y., & Guan, Q. (2023). Long-Term Performance Evaluation of BeiDou PPP-B2b Products and Its Application in Time Service. Remote Sensing, 15(5), 1358.
(4) Namie, H., & Kubo, N. (2021). Performance evaluation of centimeter-level augmentation positioning L6-CLAS/MADOCA at the beginning of official operation of QZSS. IEEJ Journal of Industry Applications, 10(1), 27-35.
(5) Yu, D., Ji, B., Liu, Y., Wu, S., Li, H., & Bian, S. (2023). Performance assessment of RTPPP positioning with SSR corrections and PPP-AR positioning with FCB for multi-GNSS from MADOCA products. Advances in Space Research, 71(6), 2924-2937.
(6) Fernandez-Hermandez I., Damy S., Susi M., Martini I., Winkel J.O., Cancela-Diaz S., Chamorro-Moreno A., Calle-Calle J., Javier de Blas F., Simon J., Blonski D., Ibanez Izquierdo- D., Galileo Authentication and High Accuracy: Getting to the Truth – Inside GNSS – Global Navigation Satellite Systems Engineering, Policy, and Design, February 13, 2023.
(7) Fernandez-Hermandez I., Chamorro-Moreno A., Cancela-Diaz S., Calle-Calle J., Zoccarato P., Blonski D., Senni T., Javier de Blas F., Hernandez C., Simon J., Mozo A., Galileo high accuracy service: initial definition and performance, GPS Solutions, Volume 26, 65, 2022.
(8) Galileo Services—High Accuracy Service Performance Report April-May-June 2023 (gsc-europa.eu).
(9) Yi, D., Bisnath, S., Naciri, N., Javier de Blas, F., & Capua, R. (2023). Galileo HAS: A Performance Assessment in Urban Driving Environments. Inside GNSS, 2023/12/07.
(10) Zhou, P., Xiao, G. & Du, L. Initial performance assessment of Galileo High Accuracy Service with software-defined receiver. GPS Solut 28, 2 (2024). https://doi.org/10.1007/s10291-023-01540-3.
(11) Galileo High Accuracy Service, Service Definition Document (HAS SDD), Issue 1.0, January 2023. European Union 2023. https://doi.org/10.2878/265974.
(12) Galileo High Accuracy Service Signal-In-Space Interface Control Document (HAS SIS ICD) (gsc-europa.eu).
(13) ftp://igs.ign.fr/pub/igs/data
(14) https://l6msg.go.gnss.go.jp/
(15) ftp://igs.ign.fr/pub/igs/products/mgex
Authors
Victor Clamadieu is responsible for navigation algorithms and GNSS performance evaluation at Thales Alenia Space in Toulouse, France. He holds an engineering degree and the MSc Aerospace Systems Navigation and Telecommunications from Ecole National de l’Aviation Civil (ENAC) in France. Its activities include GNSS systems and augmentation systems such as Satellite Based Augmentation Systems and Precise Point Positioning correction services.
Julie Antic is a specialist in GNSS integrity algorithms and performances at Thales Alenia Space in Toulouse, France. She holds a Ph.D. in probability and statistics from Paul Sabatier University, France, as well as an engineering degree in applied Mathematics from INSA in Toulouse, France. Her areas of activity include advanced GNSS augmentation systems for high accuracy and integrity, advanced receiver autonomous integrity monitoring and overbounding concepts.
Pedro Roldan is a specialist in time and frequency systems at Thales Alenia Space in Toulouse, France. He holds a Ph.D. in climatology and two master’s degrees in aerospace engineering and in meteorology and geophysics from the University of Madrid, Spain. His areas of activity include GNSS orbit determination and time synchronization algorithms, applications of GNSS for precise positioning and timing, and algorithms for time transfer, generation and steering of timescales.
Sébastien Trilles is an expert in orbitography and integrity algorithms at Thales Alenia Space in Toulouse, France. He holds a Ph.D. in pure mathematics from the Paul Sabatier University and an advanced master’s degree in Space Technology from ISAE-Supaero. He heads the Performance and Processing Department where high precise algorithms are designed including orbit determination, clock synchronization, time transfer, reference time generation, integrity and ionosphere modelling algorithms for GNSS systems and augmentation.