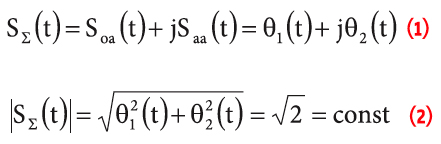
Working Papers explore the technical and scientific themes that underpin GNSS programs and applications. This regular column is coordinated by Prof. Dr.-Ing. Günter Hein, head of Europe’s Galileo Operations and Evolution.
Working Papers explore the technical and scientific themes that underpin GNSS programs and applications. This regular column is coordinated by Prof. Dr.-Ing. Günter Hein, head of Europe’s Galileo Operations and Evolution.
The theory of optimal alignment of GNSS navigation signals is evolving. While current GNSS efforts assume signals to be on only one carrier frequency, varying amplitudes of more than two signals can greatly reduce system efficiency. Alignment of these amplitudes can reduce system losses provided that the best signal combination is chosen. This column reviews applicable alignment methods and proposes a new methodology for selecting the optimal signal combination.
GNSS current development assumes the broadcasting of a set of binary navigation signals on one carrier frequency. The sum of two or more signals has varying amplitude that reduces the power amplifier efficiency. This effect results in the need for aligning the group signal amplitude.
This article presents the comparison of optimal aligning with other well-known alignment methods (such as alternate binary offset carrier —AltBOC — or interplex modulation) and includes an overview of signal alignment methods. The discussion will introduce a new symmetrized signals class, ensuring significant reductions in the aligning loss factor, is introduced. For instance, use of interplex modulation for three equipollent binary phase signals results in 25 percent power loss, while optimal aligning with symmetrization provides for only 12.7 percent loss. The use of optimal aligning for four signals yields a loss of 14.64 percent.
The article also describes our methodology for choosing the best signal combination. As an example, optimal combinations of three and four signals were discovered. Further, it also proposes design for GLONASS L3 and L5 signals based on summarizing the AltBOC signal.
Introduction
The navigation signals emitted by the first generation of GLONASS and GPS satellites were binary signals located on two carrier wave quadratures. One of these quadratures was allocated for the open access signals, Soa(t), and another one for the authorized access signals, Saa(t):
See Equation (1) (inset photo, above right)
where θi(t) = ±1, are the binary code sequences. Meanwhile, if we have arbitrary binary signals, θ1(t) and θ2(t), the amplitude of the composite signal is kept constant:
See Equation (2) (inset photo, above right)
and only the phase of the composite signal changes.
This is a particularly important property for the efficient operation of the power output satellite-signal amplifier. Efficiency of this amplifier in linear mode, which is necessary for signal amplification with variable amplitude, suddenly decreases in comparison with the saturation mode where signal amplification with a constant amplitude is possible.
In further GNSS development, the necessity of structural enhancement of the signals transmitted on the same carrier arose. New and more effective modulation types were created. Use of signal division for open- and authorized-access transmissions on pilot and data components was suggested to provide increased interference immunity of the user equipment (UE).
For the purpose of maintaining the operability of earlier UE models (“backwards compatibility”), the emission of “legacy” signals must be continued invariably for a long time. This all requires the emission of more than two binary signals on one carrier frequency.
However, the sum of more than two independent binary composite signals has a variable amplitude. The different means of alignment of the amplitude leads to different energy losses and introduces the possibility of mutual interference between the components of the composite signal. Hence, the need arose to find optimal methods for the sum alignment of binary complex signals. The first task is providing minimum energy losses. The second task is researching the value of possible mutual interferences and possible power redistribution between the component signals of the sum.
An obvious solution to sum alignment task for new signals consists of the application of their time-division multiplex. Such decisions are already applied in the current GLONASS system and GPS L2C signals. In this case, energy losses on alignment equal zero. However, the time-division multiplex has a number of essential faults. Time-division multiplex cannot be applied for augmentation of the legacy signals’ structure, and we cannot augment the signals generated on the basis of time-division multiplex in the future. For this reason, in this work we consider the alignment methods of binary composite signals other than time-division multiplex.
Review of Current Alignment Methods
In the literature we can find the following methods applied for signal alignment in different initial conditions: interplex modulation and AltBOC modulation (For full citations, see the Additional Resources section near the end of this article): Interplex modulation was proposed by U. T. Butman for the alignment task solution when the third noncorrelated binary signal θ3(t) is added to the two previously noncorrelated binary signals θ1(t), θ2(t) located on different quadratures of the carrier. This third signal sums with the signal located on one of the quadratures and, as a result, forms the composite signal SΣ(t). For SΣ(t) alignment, the leveling signal, e(t), is added into another quadrature . . .
. . .
The interplex method α1 = α2 = α3 = 1 for is illustrated with the fourth part of the vector diagram, where θ1(t) = θ2(t) and θ3(t) = ±1. The remaining three parts of the diagram are situated symmetrically. In Figure 1, thick lines show the sum vector, SΣ(t), for the cases when θ3(t) = ±1. The dotted lines identify the vectors of the leveling signal e(t), also for the cases when θ3(t)=±1. The amplitude of the alignment sum Sout(t), equals two and the directions along axis I and Q take equal parts of time. This fact proves that signal amplitudes at the outputs of navigation receiver correlators under the action of sum alignment, Sout(t), will be equal to its input.
. . .
AltBOC modulation was developed for the transfer of two independent pairs of orthogonal binary signals, located on close carrier frequencies, via common antenna. If we amplify these signals separately, we should carry out band-pass filtering of each one before their integration for emission. Due to the closeness of carrier frequencies, such a filtration leads to inadmissible distortions in emitted signals. These distortions are removed by means of common signal generation from two independent signals followed by signal amplification in one power amplifier. This option provides the necessary common signal alignment.
. . .
The foregoing review demonstrates the unsatisfactory status of sum alignment theory of navigation signals in GNSS. The various alignment methods do not have a common theoretical basis and have been developed by the designers based on an intuitive approach. Alignment principles serving as the basis of AltBOC modulation remain unclear.
Synthesis of Alignment Methods Based on LCA Minimum Criterion
. . .
Clearly, then, only the relative correlation between amplitudes SΣ(t) and Sal(t) is important and not the absolute value of the amplitude С of the aligned signal. For this reason, we will take on a value Copt = 1. With this proviso, we have proved a very simple, but not quite expected result: generation of the optimally aligned composite signal is carried out by means of a simple and well known procedure of tight restriction of the composite signal . . .
. . .
We would like to note that if the earlier input minimum criterion of LCA is added to the requirement of equality of correlator outputs of the navigation receiver, then the method of optimum alignment changes considerably. For example, with a numerical search method, the optimal alignment of a three-component sum of signals is determined to be {ψi} = {0,0,π/2} based on the criterion of minimum coefficient of losses and equivalence of correlator outputs of navigation receivers, which leads to phase values of the composite signal {φi} = {0,π/2}. In such a case, we reach minimum LCA which equals 0.25. This exactly corresponds to alignment with the interplex modulation method wherein the vectors’ phases of the composite signal, SΣ(t), are changed.
Effect of Optimally Aligned Composite Signal on Receiver Correlators
. . . we can see that value of correlator outputs from navigation receivers under the effect of the composite signal Sal(t) at the input equals the sum of outputs of the same correlators under the effect of the misaligned composite signal SΣ(t) at the same input. This condition is only exactly correct for the sum of the inputs and in the general case is not correct for the output of each separate correlator.
Next we will consider the so-called symmetric signals with the optimal alignment that keeps constant not only the sum of correlator outputs but also the outputs of each correlator.
Symmetrical Sums of Binary Composite Signals
. . . at the outputs of correlators in the case of the influence of an optimally aligned symmetrical sum, we receive the same value as in the case of influence for a non-aligned sum, SΣ(t). This property of the symmetrically aligned sums of signals generally is not incident to arbitrary asymmetrically aligned sums with signal power rescheduling at the outputs of correlators corresponding to components of the sum.
In a later section, we consider the method of construction of the symmetric sums of signals (symmetrization method) from any asymmetrical sums.
The symmetrical sums of composite binary signals with optimal alignment represent the signals with phase modulation. Therefore, for convenience later on, we will refer to these as multicomponent signals with phase modulation (MSPM).
Examples of Symmetrical Sums of Complex Binary Signals
. . . The considered examples of three- and four-component MSPM signals show how to construct five-, six-, etc., component MSPM signals.
Symmetrization Method of Arbitrary Sum Signals
We pointed out earlier that for asymmetrical sums of signals, in the course of carrying out the optimal alignment, the energy redistribution of the aligned signal between the correlators occurs. . . .
. . .
Unfortunately, the permutation of component signals between the quadratures assumed in the symmetrization method is impossible for existing GNSS signals, and in the general case for the users it is equivalent to changing a signal with two-phase modulation (BPSK) to a signal with four-phase modulation (QPSK). A later section considers from a GNSS user’s perspective the particular variants of symmetrization that are not brought to such modification of two or three signals.
. . .
Optimal Phases for Multi-Component Signal Sums Using Minimum LCA Criterion
By the method of numerical search and also using numerical sorting of all phases ψi, we found the optimal value of the phases for three- and four-component sums of the signals providing the minimum value of LCA in the course of optimal alignment as described earlier. For three-component signals at any ratio of amplitudes, only one minimum is reached at {ψi} = {0, 0, π/2} or any other permutation of phase components (asymmetrical signal). Thus for equal amplitudes, the minimum LCA value is equal to η =0.1273.
. . .
Synthesis of AltBOC Signal
. . . For the prospective signals L3 and L5 in the GLONASS system, we propose frequencies that are equal to 1175 fb and 1150 fb (fb = 1.023 MHz), respectively, and we also apply two-component signals with symbol duration of ranging code τ = 1/10fb. The application of the AltBOC signal with its symmetrical subcarriers is assumed to generate the carrier on f0=1162.5 fb frequency. Such a value is inconvenient for the frequency synthesizer and gives rise to increasing phase noise within that system element.
. . .
Alignment of Three-Component Signal
Alignment of the three-component signal is necessary for both the L1 GPS signal and the E6 and E1-L1-E2 Galileo signals. Let us specifically consider the opportunities of alignment for the three-component signal, which differ from the symmetrization method. These are based on application of signal type: SΣ(t) = θi(t) + jθ2(t) + αθ3(t)ejδ(t), where the δ(t) equiprobably accepts 0 and π/2 values. Contrary to interplex modulation, the complex-valued vector of signal αθ3(t)ejδ(t) interchangeably takes quadratures with signals θ1(t) or θ2(t). Therefore, the optimal alignment keeps the signal powers equal, θ1(t) and θ2(t), in the outputs of the respective correlators.
. . .
Conclusion
The theory of optimal alignment of the GNSS navigation signals sum is developing. A review of applicable alignment methods is presented. Alignment methods for the synthesis of summarized signals on the LCA minimum criterion is developed. Examples of sums of composite signals are considered. Symmetrization methods of arbitrary signal sums are also considered. Concrete examples of new GLONASS signal synthesis are proposed.
For the complete story, including figures, graphs, and images, please download the PDF of the article, above.
Additional Resources
[1] Avila-Rodriguez, J.-A. “The MBOC Modulation: The Final Touch to the Galileo Frequency and Signal Plan,” Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2007), Fort Worth, Texas USA, September 25–28, 2007
[2] Betz, J., “The Offset Carrier Modulation for GPS Modernization,” Proceedings of The Institute of Navigation 1999 National Technical Meeting, San Diego, California USA, January 1999
[3] Butman, U. T., “Interplex – An efficient Multichannel PSK/PM Telemetry System,” IEEE Transactions on Communication, Vol. 20, No. 3, June 1972
[4] CNES Technical Note DTS/AE/TTL/RN – 2003-48, “Spectral Control with Constant Envelope Modulations Application to Galileo BOC Signals in E2-L1-E1,” 2003
[5] Dafesh, P. A., S. Lazar, T. M. Nguyen, “Coherent Adaptive Subcarrier Modulation (CASM) for GPS Modernization,” Proceedings of the 1999 National Technical Meeting of The Institute of Navigation (ION NTM 1999), San Diego, California USA, January 1999
[6] European GNSS (Galileo) Open Service, Signal in Space Interface Control Document, European Union, 2010
[7] Global Navigation Satellite System (GLONASS) Interface Control Document, (Edition 5.1)
[8] Hein, G. W., J. Godet, J.-L. Issler, J.-C. Martin, P. Erhard, R. Lucas-Rodriguez, T. Pratt, “Status of Galileo Frequency and Signal Design,” Proceedings of ION GPS 2002, Portland, OR, September 24–27, 2002
[9] Hein, G. W., “A Candidate for the Galileo L1 OS Optimized Signal,” Proceedings of the 18th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2005), September 23–16, 2005
[10] Ipatov, V.P., Shebshaevich B.V. “Spectrum-Compact Signals: A Suitable Option for Future GNSS,” Inside GNSS, Vol. 6, No 1, pp. 47–53, January/February 2011
[11] Lestarquit, L., G. Artand, L.-L. Issler, “AltBOC for Dummies or Everything You Always Wanted to Know About AltBOC,” Proceedings of the 21st International Technical Meeting of The Institute of Navigation (ION GNSS 2008), Savannah, Georgia USA, September 16–19, 2008
[12] Navstar Global Positioning System, Interface Specification, IS-GPS-200, Revision D, IRN-200D-001, Navstar GPS Space Segment/Navigation User Interfaces, March 7, 2006
[13] Robeyrol, E., C. Macabiau, L. Ries, J. L. Issler, M. L. Bouchet, “Interplex Modulation for Navigation Systems at the L1 Band,” Proceedings of the 2006 National Technical Meeting of The Institute of Navigation (ION NTM 2006), Monterey, CA, January 18–20, 2006




