The payload will augment existing GNSS constellations with additional navigation signals from LEO, while relying on GNSS for orbit determination and time synchronization.
FLORIAN KUNZI, BENJAMIN BRAUN, MARKUS MARKGRAF, OLIVER MONTENBRUCK, GERMAN AEROSPACE CENTER (DLR) / GERMAN SPACE OPERATIONS CENTER (GSOC)
WALTER FRESE, RAPID CUBES GMBH
The GNSS market has grown rapidly over the last decades. Consequently, the number of users and applications relying on GNSS is larger than ever. However, applications, especially safety-critical applications, suffer from the low signal strength and resulting threat of jamming, as well as the ease of spoofing. This vulnerability led to low Earth orbit (LEO) becoming a potential complement for satellite navigation. Over the past years, agencies and industry all over the world have carried out large efforts to develop solutions for positioning, navigation and timing (PNT) services from LEO. Furthermore, the New Space paradigm with its emerging private space industry and commercialization of services from space has enabled mega-constellations in LEO with hundreds to thousands of satellites, offering potential platforms for PNT services. The realization of LEO PNT has been discussed extensively in literature, with three general architectures having emerged: Hosted satellite navigation payloads specifically designed for PNT services [1], fused payloads integrated in existing telecommunication payloads [2] and leveraging arbitrary signals of opportunity from LEO for navigation without the need for a dedicated space segment [3].
Following the architecture of a hosted payload, we present the concept and development progress of a potential LEO PNT system. The payload aims to augment existing GNSS constellations with additional navigation signals from LEO, while simultaneously relying on GNSS for orbit determination and time synchronization (ODTS). Except for GNSS, the payload remains autonomous from any external data source to minimize the requirements on both satellite bus and ground segment, improving flexibility, scalability and cost-efficiency. Its tight time and frequency synchronization to existing GNSS constellations ensures compatibility and inter-operability. No dedicated ground segment is needed, while the requirements for space infrastructure are kept at a minimum. The payload is intended to have a small footprint, and comprises a multi-frequency, GPS/Galileo receiver, a chip-scale atomic clock (CSAC), a navigation computer and a signal generator. The components can largely be based on commercial off-the-shelf (COTS) hardware, improving cost-efficiency and scalability for large satellite constellations.
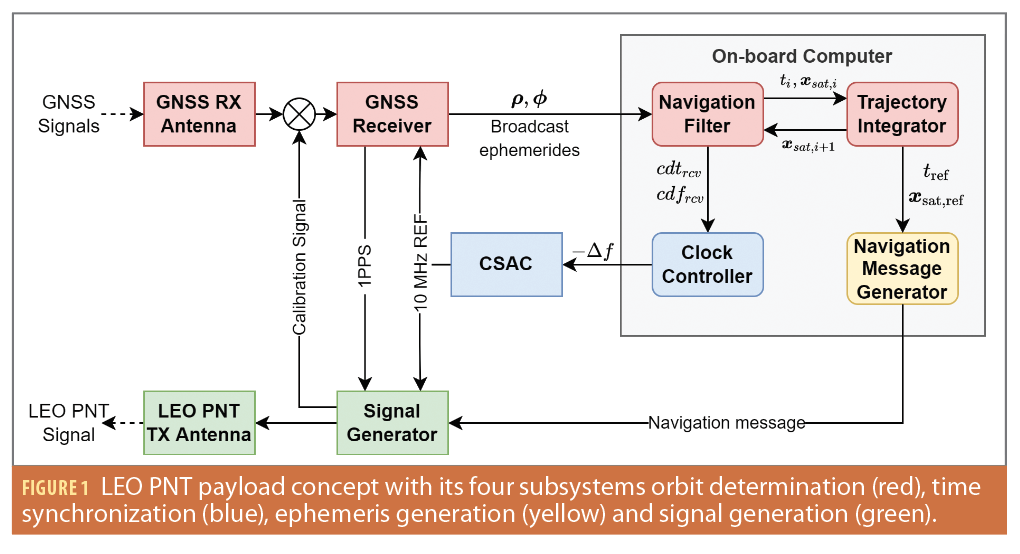
The payload concept is depicted in Figure 1. GNSS observables are processed by a real-time navigation filter for precise ODTS. The predicted satellite trajectory is used to generate the satellite’s ephemeris. The CSAC is a key payload component, serving as on-board time and frequency reference for both GNSS receiver and signal generator. Its phase and frequency are continuously steered toward a GNSS broadcast time using the on-board navigation solution. An absolute synchronization of the signal generator’s phase with respect to GNSS is ensured with an internal calibration signal. This ultimately allows generation of GNSS-synchronized ranging and navigation signals, which can be employed for navigation in combination with GNSS signals for single point positioning (SPP).
Realtime Navigation System
For any LEO PNT concept, achievable user navigation performance ultimately depends on the availability and quality of real-time ephemerides, i.e. the orbit and clock data for the individual LEO satellites. The presented concept uses GNSS to autonomously determine the instantaneous LEO orbit and GNSS broadcast time on-board the satellite using an extended Kalman filter (EKF). A reduced dynamics orbit model [4] with empirical accelerations is applied during the time update to propagate the satellite orbit. The navigation filter state is defined as

where rsat and vsat are the satellite’s position and velocity in the International Celestial Reference Frame (ICRF), respectively. The filter processes measurements from both GPS and Galileo, with either one able to serve as the primary system. Thus, the receiver clock offset cdtrcv in units of distance referring to the primary system needs to be complemented by an inter-system bias (ISB) cdtISB to account for the differences between GPS Time (GPST) and Galileo System Time (GST). In addition, the receiver clock drift cdfrcv is estimated. For the orbit model, the satellite’s atmospheric drag and radiation coefficients cD and cR are estimated as dimensionless parameters. Furthermore, as the orbit model does not incorporate all forces acting on the satellite, an empirical acceleration vector aemp with radial, along- and crosstrack (RAC) components is estimated. Finally, carrier-phase float ambiguities and estimated signal-in-space range errors are aggregated in the vector Namb.
The navigation filter processes ionosphere-free linear combinations of GPS L1CA/L2C and Galileo E1c/E5a code and phase observations. Prior to the measurement update, outliers are identified and excluded using least-squares. The ionosphere-free pseudorange and carrier-phase combinations are modeled using the geometric range between GNSS satellite and receiver antenna phase centers. The receiver clock offset and drift are corrected with the respective satellite clock offset. To account for the different system time scales of GPS and Galileo, the estimated ISB dtISB is applied for the secondary GNSS to align the measurements with the primary system’s time scale. For the pseudorange model, differential code biases need to be applied in case of the GPS L1CA/L2C signal combination. The carrier phase requires consideration of the respective estimated float ambiguity and phase wind-up. Due to the use of broadcast ephemeris, no satellite antenna phase center offsets need to be applied in the measurement model. Furthermore, the ionospheric delay of the signals is eliminated to first order by forming ionosphere-free combinations and thus can be omitted in the model as well.
During the filter time update, the ISB, clock drift, radiation and drag coefficients and the float ambiguity vector are propagated as constants with white Gaussian noise, while a linear model is employed using the clock drift for the receiver clock offset. For the remaining state vector components—including the satellite’s position and velocity, the empirical accelerations as well as drag and radiation pressure coefficients—a reduced dynamics orbit model and variational equations are used for propagation [4,5]. The acceleration asat acting on the satellite is modelled using the gravitational potential up to order and degree 70, third-body forces of sun and moon with low-precision ephemeris, an approximation of the atmospheric drag based on the Harris-Priester model [6], a simplified solar radiation pressure model as well as K2 Earth solid tides. The resulting differential equation for the satellite state vector is solved using the 5th-order numerical integration method by Dormand and Prince (DP5) [7], which yields smooth interpolants without additional function evaluations, and hence allow to reconstruct the satellite’s trajectory at an arbitrary epoch within the integration time interval. Therefore, in contrast to a purely kinematic precise point positioning [8], the real-time navigation system not only determines the instantaneous satellite state at the individual measurement epochs, but provides a continuous representation of the LEO trajectory at all intermediate times and across data gaps.
Additional and time-varying information is required by the filter during the update stages. To retain autonomy of the navigation payload, it is desirable that such data can be retrieved via the GNSS broadcast navigation messages. The GPS CNAV message transmitted on the L2C signal provides Earth orientation parameters (EOP) as well as timing group delays (TGD) and inter-signal corrections (ISCs) required by the real-time navigation system. While the satellite state is tracked in ICRF, the navigation system also needs to convert the state to International Terrestrial Reference Frame (ITRF) for both force and measurement models. The time-varying transformation matrix required for this step can be obtained with the EOP. Code biases between the employed L1CA/L2C combination and the clock reference signals L1/L1 P(Y) are corrected in the modeled code range using the respective satellite’s TGD and ISC parameters [9]. The Galileo system time, on the other hand, refers to the E1/E5a signal combination used by the payload, and thus no bias corrections are needed. Furthermore, while the F/NAV message also provides a GPS-Galileo Time Offset (GGTO) for a transformation between GST and GPST, this parameter is only provided as a daily linear approximation. The on-board navigation system instead employs a more accurate aggregated user GGTO, which is continuously estimated by the navigation filter as ISB parameter and also incorporates receiver-specific biases [10]. Finally, in contrast to common precise point positioning (PPP) applications, the navigation filter uses only broadcast ephemerides to obtain GNSS satellite orbit and clock information. Therefore, the navigation payload remains independent from any additional data streams and only relies on the GPS CNAV and Galileo F/NAV broadcast navigation messages.
Time Synchronization
The time synchronization subsystem with the CSAC as on-board time and frequency reference represents a key component in the overall payload design. In contrast to the highly stable atomic clocks on board GNSS satellites, the here employed Microsemi SA.45s is several magnitudes less stable with an Allan deviation (ADEV) in the order of 10-10 to 10-11 for sample times between 1 to 1,000 s. For GNSS, users can predict clock offsets with second order polynomials over validity intervals of up to several hours. With pass durations of LEO satellites being less than 20 minutes for terrestrial observers, the statistical uncertainty of the CSAC’s timing error would exceed 10 ns or 3 m, rendering a polynomial clock prediction unfeasible for the payload. To minimize this statistical error, the clock state obtained from the navigation filter is used to align the CSAC’s output frequency with a highly stable GNSS time scale by continuous clock steering. With the CSAC serving as frequency reference for the GNSS receiver, clock offset and drift estimated by the navigation filter consequently correspond to the CSAC’s phase deviation and fractional frequency offset with respect to GNSS broadcast time. In this way, the mid- to long-term instabilities of the CSAC due to random walk frequency modulation (RWFM) are compensated, while maintaining the short-term stability of the CSAC itself. With the synchronized CSAC output frequency, the payload can generate signals synchronized to GNSS at low nanosecond level, allowing them to be used in combination with existing GNSS signals. A precise time synchronization of the navigation payload with respect to GNSS broadcast time effectively omits the requirement for a proprietary time scale within the LEO PNT system. Such an approach can drastically reduce the requirements on a ground segment. As in combination with on-board orbit determination, the payload’s autonomy is increased to a point where nominal ODTS operations are performed solely on the satellite.
Satellite Ephemeris
Analogous to GNSS broadcast ephemerides (BCE) transmitted via the navigation signals, a LEO PNT system needs to provide its satellite’s instantaneous position and clock to users. Two essential differences compared to medium Earth orbit (MEO) need to be considered: on one hand, the orbit dynamics strongly differ between MEO and LEO, rendering the 16-parameter perturbed Keplerian element model used by GPS and Galileo unfeasible to adequately model LEOs for trajectory prediction. On the other hand, LEO satellites are visible for very limited time periods of up to about 20 minutes for users on Earth. Thus, the validity time can be much shorter compared to GNSS, where ephemerides are usable for several hours before they expire. Previous research has already assessed a wide range of different ephemeris formats for LEO with a sufficient precision for PNT services, such as an extension of the GNSS models with additional parameters [11], numerical integration of satellite state vectors [12] or polynomial fitting [13]. The payload concept proposed here can take advantage of the trajectory information already available from the orbit propagator to provide a compact and efficient ephemeris format. With representative filter update steps of 30 s, the navigation message can be frequently refreshed to minimize the impact of extrapolation errors. Thus, for short validity intervals of up to one minute, a simple 6th-order polynomial ephemeris model similar to SBAS can be used for a centimeter-level orbit representation. Based on fixed polynomial interpolation nodes, a computationally efficient least squares fitting can be performed on-board to obtain polynomial coefficients. However, this method is not suitable to predict an entire LEO satellite pass of up to 20 minutes, as the number of coefficients would need to be increased drastically to retain the level of precision. Thus, if longer validity intervals were desired, a more sophisticated ephemeris model based on state vector integration or perturbed Keplerian elements would need to be employed.
Besides the position, users also need to be able to predict the satellite’s clock offset with respect to a well-defined system time scale. In view of the payload’s tight synchronization to GNSS broadcast time, the need for clock prediction and a dedicated clock offset polynomial is essentially avoided. Instead, users can assume the CSAC to be perfectly synchronized with the main GNSS broadcast time used by the payload, i.e. having zero clock offset and drift. The performance of this zero-clock ephemeris model then solely relies on the time synchronization subsystem’s precision.
With information about the satellite’s trajectory, either as a polynomial for short-term prediction or in more complex formats, the payload can autonomously generate a light-weight broadcast navigation message. As no clock information is needed, the message contents can be limited to trajectory information. Depending on performance and requirements, the message can be updated autonomously on-board after each filter epoch. The fast update rate ensures high quality ephemeris for users. However, in case of short validity intervals, receivers must continuously track the data signal and decode the navigation message. Thus, the selection of ephemeris format and validity intervals ultimately depends on user equipment and requirements.
Signal Generation and Calibration
By disciplining the CSAC to GNSS time and thus improving its long-term stability, the 10 MHz output can be used directly as a frequency reference for the signal generator. Proper alignment of the generated signals with the GNSS time scale is initially achieved through the one pulse-per-second (PPS) signal issued by the on-board GNSS receiver. However, PPS precision is not sufficient for the payload’s intended performance level. For this reason, a continuous nanosecond-level synchronization is foreseen in the present payload concept with a calibration signal after the coarse PPS alignment. Using established GNSS modulations, the signal is provided by the signal generator and fed into the GNSS receiver. Based on measurements of the calibration signal and comparison with those of the actual GNSS satellites, the navigation filter can monitor possible systematic phase offsets of the locally generated navigation signals and ensure full synchronicity with GNSS time to the desired accuracy.
Preliminary System Performance Assessment
Performance of on-board ODTS concepts have been assessed in previous studies. With ionosphere-free combinations of dual-frequency GPS/Galileo code and carrier phase measurements, a 3D orbit root-mean-square (RMS) error of approximately 10 cm as well as sub-nanosecond timing precision have been demonstrated [10, 14, 15]. These studies also emphasize the significant benefit of the high quality and frequently updated Galileo broadcast ephemerides on the achievable level of performance. Based on these results, a preliminary evaluation of the achievable signal-in-space ranging error (SISRE) can be conducted for an estimation of payload performance. The payload’s time synchronization concept using a closed loop control system was evaluated in a previous study using a Microsemi SA.45s CSAC and a static, terrestrial GNSS receiver [16]. With GPS and Galileo observables, sub-nanosecond time interval errors (TIE RMS) as well as maximum time interval errors (MTIE) below 5 ns could be achieved within sampling intervals of 3,000 s for control time steps of up to 30 s. However, a proper and continuous bias compensation requires a hardware calibration prior to launch, as well as a self-calibration routine that can be performed autonomously in orbit.
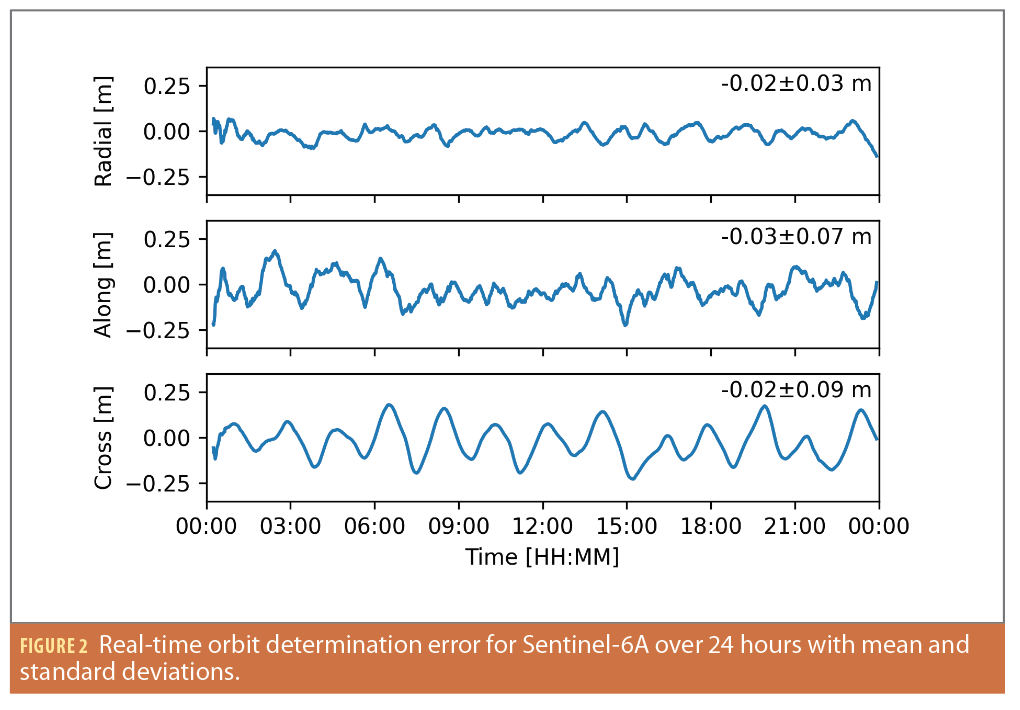
As no real flight data is available yet for the ODTS, a preliminary SISRE evaluation is performed using combined results of LEO real-time orbit determination and terrestrial CSAC clock steering. With the previously described navigation filter, a simulated real-time orbit determination of the Sentinel-6A spacecraft at 1,337 km altitude was performed for 24 hours using real observation data. As seen in Figure 2, the standard deviations in radial, transverse and normal (RTN) axes are below 10 cm in all three axes. Characteristic oscillations with a period of once-per-revolution can be observed in the radial and cross-track components.
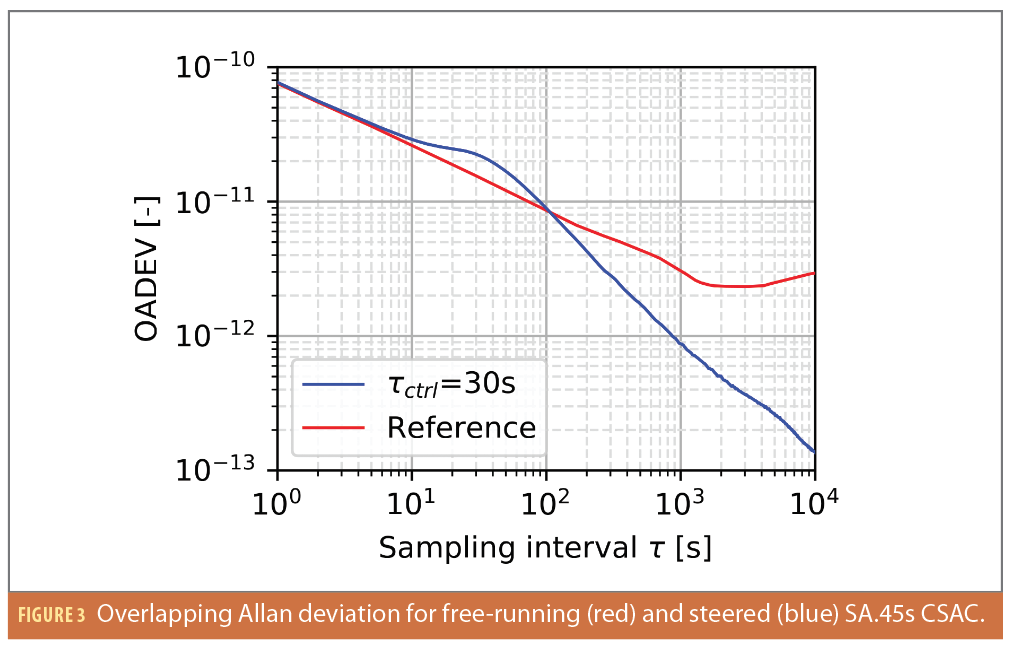
The time synchronization was conducted in real-time over 24 hours using a Microsemi SA.45s CSAC in a terrestrial setup as described in [16], which is similar to the payload’s TS subsystem. The overlapping Allan deviation (OADEV) depicted in Figure 3 is governed by the CSAC’s short-term stability for sample times lower than the control interval τctrl=30 s, and exhibits an expected decrease in stability around the control interval compared to the free-running CSAC due to the steering process. Beyond τctrl, however, the CSAC’s stability is significantly improved by the steering process.
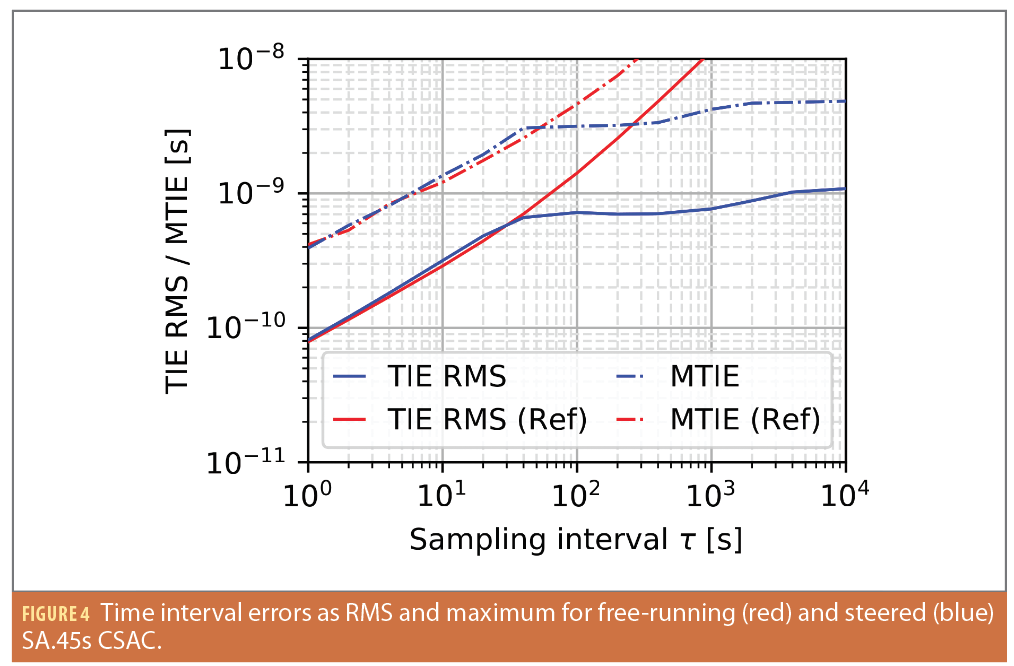
As seen in Figure 4, the time interval error (TIE) RMS for a typical LEO satellite pass with less than 20 minutes or 1,200 s is 1 ns, while the maximum TIE (MTIE) does not exceed 5 ns. The TIE RMS converges to around 1 ns, which presumably represents the current limit of GNSS broadcast time access with broadcast ephemerides. Furthermore, the TIE effectively determines the statistical clock error for a user under the assumption of zero clock offset and drift.
Based on the results of both orbit determination and time synchronization, an assessment of the SISRE achievable by the ODTS system is carried out. The SISRE in units of distance can be expressed as

where R, A and C represent the orbit errors in RAC frame, respectively, and is the timing error. In contrast to SISRE analysis for GNSS satellites in MEO [17], the radial and timing errors need to be decoupled for LEO as it can’t be assumed the user-satellite line of sight and the radial orbit component are aligned. Furthermore, the dimensionless weight factors w1 and w2 depend on the orbit altitude and can be roughly approximated by w1=w2=1/√3 for LEOs.
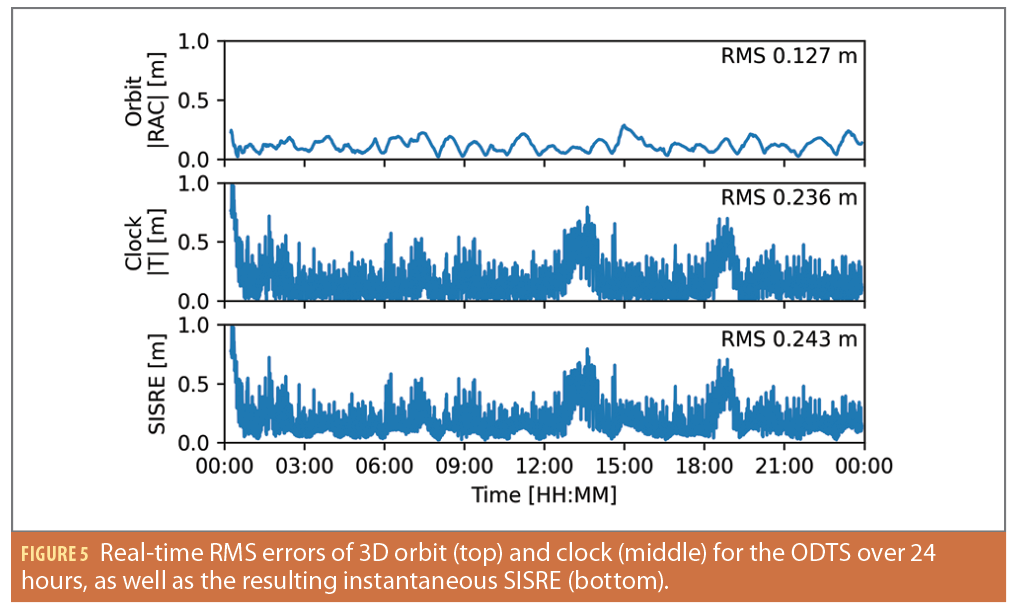
Figure 5 shows the 3D orbit RMS error (top) as well as the absolute clock error (middle). The clock error exhibits a significantly stronger short-term noise compared to the orbit error, as well as long-term variations with peak variations of up to 1 m and a standard deviation of 24 cm or 0.77 ns. The resulting instantaneous SISRE over the 24-hour time interval is depicted in the lower plot of Figure 5. As expected, the timing error dominates the overall SISRE in both short- and long-term variations. Note the Sentinel-6A altitude is comparatively high for a LEO satellite and the orbit determination RMS error for lower satellites tends to be worse due to more complex orbit perturbations. However, the clock error of the steered CSAC will remain the prevailing SISRE component independent of the LEO altitude. Thus, significant improvements in the overall ODTS performance would presumably require a more stable on-board oscillator than the here employed SA.45s CSAC.

ODTS In-Orbit Demonstration
A first step toward a fully operational LEO PNT payload will be conducted with the Autonomous Time and Orbit Determination for Microsatellite Constellations (ATOMIC) mission, which aims to validate the ODTS subsystem in orbit. The payload will be hosted by the 12U CubeSat AIOTY-CUBE depicted in Figure 6, developed by the company Rapid Cubes GmbH. Based on the RapidCube-20 CubeSat bus platform, the satellite features an attitude control system with a pointing accuracy of <±5°, which is essential for a continuous zenith-pointing of the on-board GNSS antenna. AIOTY-CUBE is planned for launch in 2024 on the Spectrum rocket’s second flight from ISAR Aerospace.
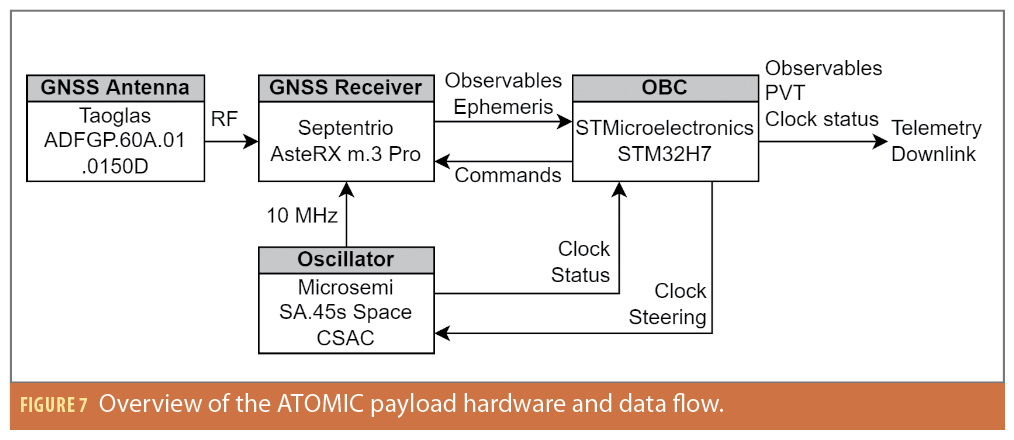
The ATOMIC payload essentially comprises the ODTS subsystem of the LEO PNT payload (Figure 1) including a GNSS antenna and receiver, a CSAC and an on-board computer (OBC) as seen in Figure 7. A main design driver of the payload is to achieve a low surface, weight and power (SWaP) for compatibility with small spacecraft as well as potential scalability for larger LEO constellation, with a mass of less than 1 kg and a maximum power consumption of 2.5 W. Following the New Space paradigm, the payload hardware was selected from commercial of-the-shelf (COTS) components and includes a Septentrio AsteRX-m.3 Pro+ GNSS receiver, a Microsemi SA.45s Space CSAC, a STMicroelectronics STM32H723 microprocessor and a Taoglas ADFGP.60A.01.0150D active all-band GNSS antenna. A power supply unit (PSU) is responsible for DC/DC conversion between the unregulated satellite bus voltage and the hardware components. Furthermore, the PSU provides separate latch-up protections for all hardware components. The GNSS receiver and antenna as well as the CSAC can be power cycled by the OBC in case of soft errors. All components are assembled on a single circuit board in an aluminum housing as seen in Figure 8. The housing features connectors for the CSAC’s disciplined 10 MHz output and its pulse-per-second (PPS) signal as well as debug and telemetry/telecommand (TMTC) interfaces to allow both a safe integration in the satellite structure and easy testing on the ground.
The flight software hosted on the OBC runs on a real-time operating system and includes the previously presented navigation filter, a clock controller as well as TMTC and data management. The telecommands will allow a limited in-orbit reconfiguration of the ODTS parameters. Telemetry includes the estimated satellite position, velocity and clock state at measurement epoch as well as the raw measurements obtained from the GNSS receiver. Furthermore, several housekeeping parameters from the CSAC will be downlinked, which potentially provide valuable information about the clock’s behavior in the space environment, especially for high radiation exposures during passes through the South Atlantic Anomaly.
ATOMIC mission’s performance evaluation will be completed in post-processing on ground. Precise reference solutions for both orbit and clock can be obtained with a least squares filter using the raw GNSS observables. This reference can then be compared to the real-time solution from the navigation filter. The target performance for the ATOMIC mission is a 20 cm 3D RMS orbit error as well as a timing precision of 2 ns. Furthermore, the availability of both reference and real-time solutions allows evaluation of different real-time ephemeris generation algorithms based on real on-board data as a next step in the design of a fully operational LEO PNT payload.
Summary and Conclusion
We presented the concept and development progress of a hosted satellite navigation payload for LEO PNT. With an expected ODTS performance of less than 20 cm orbit error and 2 ns timing precision, a SISRE comparable to today’s GNSS is achieved and sub-meter positioning becomes possible. Due to the strict synchronization to GNSS, the LEO navigation signals can be seamlessly used in combination with existing GNSS signals, offering additional geometric diversity and redundancy. Despite an inherent dependence on existing GNSS constellations, the LEO overlay system can reduce the vulnerability of stand-alone GNSS navigation caused by terrestrial jamming and spoofing by offering higher signal strengths and diverse frequencies, as well as optional signal authentication and encryption. In a first step toward a fully operational LEO PNT payload, the ATOMIC mission expected to launch in 2024 will demonstrate the ODTS in orbit.
Acknowledgements
This article is based on material presented in a technical paper at ION GNSS+ 2023, available at ion.org/publications/order-publications.cfm.
References
(1) Reid, T. G., Neish, A. M., Walter, T., & Enge, P. K. (2018). Broadband LEO constellations for navigation. NAVIGATION, Journal of the Institute of Navigation, 65(2), 205–220. https://doi.org/10.1002/navi.234
(2) Iannucci, P. A., & Humphreys, T. E. (2022). Fused low-Earth-orbit GNSS. IEEE Transactions on Aerospace and Electronic Systems. https://doi.org/10.1109/TAES.2022.3180000
(3) Kassas, Z., Neinavaie, M., Khalife, J., Khairallah, N., Kozhaya, S., Haidar-Ahmad, J., & Shadram, Z. (2021). Enter LEO on the GNSS stage: Navigation with Starlink satellites. InsideGNSS.
(4) Wu, S.-C., Yunck, T. P., & Thornton, C. L. (1991). Reduced-dynamic technique for precise orbit determination of low Earth satellites. Journal of Guidance, Control, and Dynamics, 14(1), 24–30. https://doi.org/10.2514/3.20600
(5) Montenbruck, O., & Gill, E. (2002). Satellite Orbits: Models, Methods, and Applications. Springer. https://doi.org/10.1007/978-3-642-58351-3
(6) Harris, I., & Priester, W. (1962). Time-dependent structure of the upper atmosphere. Journal of the Atmospheric Sciences, 19(4), 286–301. https://doi.org/10.1175/1520-0469(1962)019%3C0286%3ATDSOTU%3E2.0.CO;2
(7) Dormand, J., & Prince, P. (1980). A family of embedded Runge-Kutta formulae. Journal of Computational and Applied Mathematics, 6(1), 19–26. https://doi.org/10.1016/0771-050X(80)90013-3
(8) Tegedor, J., Bartle, J., Ward, J., Liu, X., Glazier, S., & van Duijn, P. (2023). In-Orbit Demonstration of Precise Point Positioning for Real-Time On-Board High-Accuracy Orbit Estimation of LEO Satellites. 37th Annual Small Satellite Conference, SSC23-X-04, 5-10 Aug. 2023, Logan, Utah
(9) Tetewsky, A., Ross, J., Soltz, A., Vaughn, N., Anszperger, J., O’Brien, C., Graham, D., Craig, D., & Lozow, J. (2009). Making Sense of Inter-Signal Corrections – Accounting for GPS Satellite Calibration Parameters in Legacy and Modernized Ionosphere Correction Algorithms. InsideGNSS.
(10) Kunzi, F., & Montenbruck, O. (2022). Precise On-board Time Synchronization for LEO Satellites. NAVIGATION, Journal of the Institute of Navigation, 69(3), Article navi.531, 531. https://doi.org/10.1002/navi.531
(11) Guo, X., Wang, L., Fu, W., Suo, Y., Chen, R., & Sun, H. (2022). An optimal design of the broadcast ephemeris for leo navigation augmentation systems. Geo-Spatial Information Science, 25(1), 34–46. https://doi.org/10.1080/10095020.2021.2017760
(12) Meng, L., Chen, J., Wang, J., & Zhang, Y. (2021b). A broadcast ephemeris design of leo navigation augmentation satellites based on the integration-type ephemeris model. Measurement Science and Technology, 32(8), 085009. https://doi.org/10.1088/1361-6501/abfaf5
(13) Dobbin, M., & Axelrad, P. (2023). A flexible ephemeris representation for GNSS and alternative PNT signal sources using B-splines. NAVIGATION, 70(4). https://doi.org/10.33012/navi.610
(14) Montenbruck, O., Kunzi, F., & Hauschild, A. (2022). Performance assessment of GNSS-based real-time navigation for the Sentinel-6 spacecraft. GPS Solutions, 26(1), 12. https://doi.org/10.1007/s10291-021-01198-9
(15) Hauschild, A., & Montenbruck, O. (2021). Precise real-time navigation of LEO satellites using GNSS broadcast ephemerides. NAVIGATION, Journal of the Institute of Navigation, 68(2), 419–432. https://doi.org/https://doi.org/10.1002/navi.416
(16) Kunzi, F., & Montenbruck, O. (2023). Precise Disciplining of a Chip-scale Atomic Clock using PPP with Broadcast Ephemerides. GPS Solutions, 27(4), 165. https://doi.org/10.1007/s10291-023-01496-4
(17) Montenbruck, O., Steigenberger, P., & Hauschild, A. (2018). Multi-GNSS signal-in-space range error assessment—Methodology and results. Advances in Space Research, 61(12), 3020–3038. https://doi.org/10.1016/j.asr.2018.03.041.
Authors
Florian Kunzi is a member of the GNSS Technology and Navigation Group at DLR’s German Space Operations Center (GSOC) and a PhD candidate at Technical University of Munich. He received his M.Sc. degree in Space Science and Technology from the University of Würzburg in 2018. His current work focuses on precise orbit determination and timing for spaceborne GNSS augmentation with LEO satellites.
Benjamin Braun has been a member of the GNSS Technology and Navigation Group at DLR/GSOC since 2013. He is working on hybrid navigation systems for sounding rocket and launch vehicle applications comprising inertial sensors and GNSS receivers. His research is particularly focused on increasing the robustness of GNSS by inertial aiding. He received his PhD on “High Performance Kalman Filter Tuning for Integrated Navigation Systems” at Technical University of Munich in 2016.
Markus Markgraf is a senior research engineer in the GNSS Technology and Navigation Group at DLR/GSOC. He started working at DLR in 2000 after graduating as Dipl.-Ing. (FH) for Electrical Engineering and Communication Technology. His current research activities comprise GNSS receiver technology for satellites and sounding rockets, scientific applications of GNSS and mission support and analysis. He was the key engineer for several GNSS navigation payloads on LEO satellites, sounding rockets and launch vehicles.
Oliver Montenbruck is head of the GNSS Technology and Navigation Group at DLR/GSOC. His research activities include spaceborne GNSS receiver technology, autonomous navigation systems, spacecraft formation flying and precise orbit determination, new constellations, and multi-GNSS processing. He presently chairs the Multi-GNSS Working Group of the International GNSS Service and coordinates the performance of the MGEX Multi-GNSS Pilot Project. He is a fellow of the Institute of Navigation (ION) and received the ION Johannes Kepler Award in 2018.
Walter Frese completed his degree in space engineering at the Technical University Berlin (TUB) in 2008. He then worked as a research assistant at the TUB and dealt with issues in the area of satellite design and in particular intersatellite communication with small satellites. In 2021, he founded the company Rapid Cubes with one of his colleagues and has since been developing small satellites and high-performance CubeSats, primarily for communications applications.






