Q: Are C/N0 Algorithms Equivalent in All Situations?
A: Fundamental to determining the status of GNSS tracking subsystems and controlling a GNSS receiver, the measure of C/N0 (carrier-to-noise ratio) provides satellite signal health information in addition to the PVT (position, velocity, time) information. For example, tracking loops experience a rapid increase of tracking errors at low C/N0, e.g., below 30 dBHz, until they completely lose lock.
Q: Are C/N0 Algorithms Equivalent in All Situations?
A: Fundamental to determining the status of GNSS tracking subsystems and controlling a GNSS receiver, the measure of C/N0 (carrier-to-noise ratio) provides satellite signal health information in addition to the PVT (position, velocity, time) information. For example, tracking loops experience a rapid increase of tracking errors at low C/N0, e.g., below 30 dBHz, until they completely lose lock.
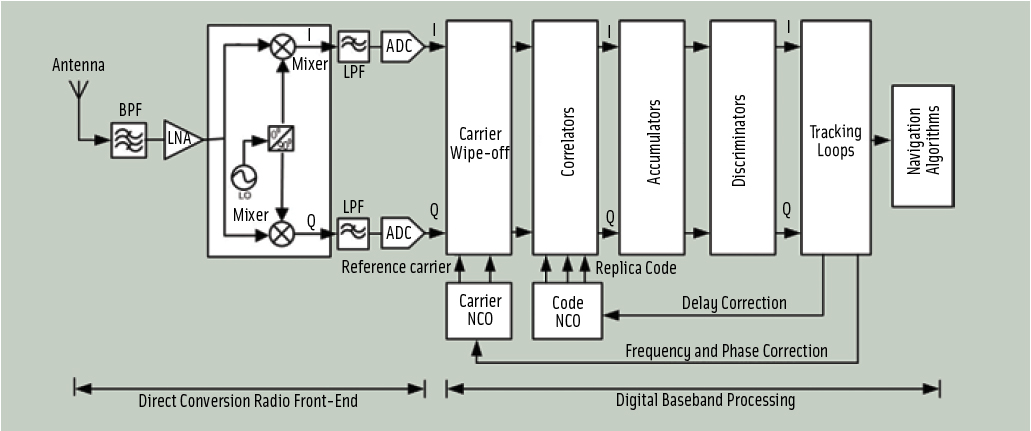
In this column, we present a comparison of C/N0 algorithm performance. In digital receivers several methods may be used to estimate C/N0, but all involve processing samples from the correlator output. Dr. Brad Badke discussed the most intuitive algorithm in the GNSS Solutions column in the September/October 2009 issue of Inside GNSS — the so-called real signal-complex noise (RSCN) method.
Texts on GPS architecture usually include another classic approach, the narrowband-wideband power ratio (NWPR) method. Additionally, literature on digital communication offers many other methods for estimating SNR (signal-to-noise ratio) — which, as discussed in Dr. Badke’s contribution is not the same as C/N0 — of M-PSK (M-phase shift keying) modulations in additive white Gaussian noise (AWGN). However, these SNR algorithms must be adapted before equating them to C/N0.
Since high-performance GNSS software receivers have become a reality in navigation labs worldwide, software engineers must select algorithms capable of maximizing accuracy with minimal implementation complexity. For this reason, in our discussion we will compare the accuracy and implementation complexity of five different C/N0 estimation algorithms.
Computational Complexity of Different Estimators
Here we will investigate the following SNR estimation algorithms:
- Real Signal-Complex Noise (RSCN)
- Beaulieu’s method (BL): an “intuitively motivated” algorithm introduced in 2000 by N. C. Beaulieu et alia
- Signal-to-Noise Variance (SNV): squared Signal-to-Noise Variance estimator, based on the first absolute moment and the second moment of the signal samples
- Moment Method (MM): employs the second- and fourth-order moments for the separate estimation of carrier strength and noise strength
- Narrowband-Wideband Power Ratio (NWPR) Method, reported in several books on GPS receivers. Note that this is the only algorithm that estimates C/N0 directly; the others estimate SNR, which can be converted to C/N0 as discussed later.
. . .
The Effect of Phase Noise
In the presence of a residual phase error (θn) in the carrier tracking loop, the above algorithms experience asymptotic biases for high C/N0 values. Such biases can be theoretically demonstrated by computing the asymptotic limit for Pd →∞ of the SNR estimators with non-zero θn. Herein, θn is assumed to be a zero-mean random variable with variance σθ² and uniform distribution between [-√3σθ, +√3σθ].
When the noise power contribution is very small, some algorithms cannot discriminate additive noise from θn or other factors, while other algorithms are sensitive to the noise power only.
On the other hand, in low SNR conditions the principal limiting phenomenon is that the carrier tracking loop no longer keeps the incoming and the local carriers synchronized. In this case the SNR algorithms use correlator outputs inconsistent with the assumed distribution of θn, thereby invalidating the SNR estimate.
However, as long as the receiver maintains signal lock and the software tracking loops are not broken, the SNR estimators perform equivalently in medium-to-low SNR conditions.
. . .
Conclusions
Several algorithms developed for SNR estimation of biphase shift keying/quad phase shift keying (BPSK/QPSK) modulations in a noisy environment can be employed to compute the C/N0 ratio in a GNSS digital receiver; however, they experience different estimation performance and implementation complexity. In particular they offer different sensitivities to the residual carrier phase noise, mainly for very high carrier-to-noise ratios. Receiver designers should select the algorithm that best suits their particular needs.
(For Emanuela Falletti, Marco Pini and Letizia Lo Presti’s complete answer to this question, including formulas and tables, please download the full article using the pdf link above.)