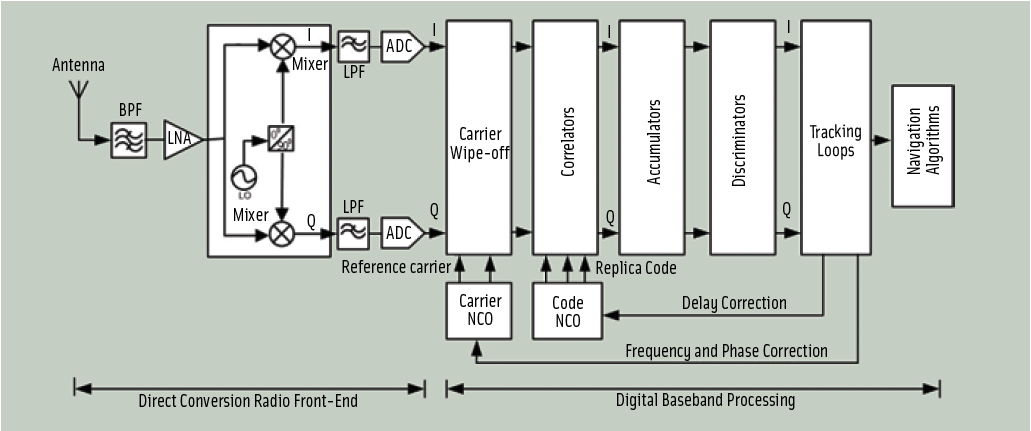
 FIGURE 1: Block-diagram of a GNSS direct-conversion receiver
FIGURE 1: Block-diagram of a GNSS direct-conversion receiver
For the complete story, including figures, graphs, and images, please download the PDF of the article, above.
GNSS systems rely on direct sequence spread spectrum (DSSS) transmissions to achieve high receiver sensitivity. Typically, GNSS user equipment compares the signal received from a satellite with an internally generated replica of its corresponding code until the maximum correlation for a given delay is achieved. This provides an indirect measurement of the satellite-receiver range.
For the complete story, including figures, graphs, and images, please download the PDF of the article, above.
GNSS systems rely on direct sequence spread spectrum (DSSS) transmissions to achieve high receiver sensitivity. Typically, GNSS user equipment compares the signal received from a satellite with an internally generated replica of its corresponding code until the maximum correlation for a given delay is achieved. This provides an indirect measurement of the satellite-receiver range.
One of the performance limiting factors of GNSS receivers is the imperfection of the radio frequency (RF) oscillator. This imperfection translates into random deviations of instantaneous phase or frequency, typically modeled as a phase imperfection, and often referred to as phase noise.
The receiver oscillator phase noise narrows the carrier tracking loop bandwidth, while diminishing the achievable carrier-to-noise ratio (C/N0). The correlation outputs in the code-tracking loop are also affected, creating correlation noise and losses at the receiver that are measured as reductions in C/N0.
Furthermore, longer integration intervals ideally result in higher sensitivity. However, because phase noise is translated into a rotation of the constellation diagram of a modulated signal that can make integration (correlation) comparatively less effective as the interval increases.
Phase noise models have been proposed for various wireless communication receivers. (See the sidebar, “Modeling Phase Noise Effects on Receivers: A History”) However, the effects of phase noise on GNSS receivers’ performance have been rarely documented, leaving key design questions unanswered: What is the maximum acceptable phase noise level as required by an RF designer in order to achieve a minimum pre-defined C/N0? How do correlation losses relate to phase noise levels?
In this article, we propose an analytical approach using a given phase noise model, validating it through simulations to quantify the effect of oscillator noise on the performance of GNSS receivers. From this we provide a first estimation of the requirements of a radio front-end for a given baseband implementation, as well as an insight into the relationship between correlation time and performance degradation due to phase noise.
The following section of our discussion provides a theoretical analysis, in both time-domain and frequency-domain, of the effect of this phase noise on various properties of code correlation.
We then perform numerical simulations of GPS L1 pseudorandom noise (PRN) code correlation for various values of phase noise in order to validate the theoretical model. Next, a datastream simulation using a Galileo E1 receiver, complete with carrier and code tracking loops, quantifies the effect of oscillator noise on GNSS receiver performance. Here, the simulated PRN code correlation in the presence of phase noise demonstrates that the model (and GPS results) may be applied to Galileo signal receivers as well.
Finally, we compare results from all the simulations and recommend a practical limit for the maximum phase noise permissible from the front-end oscillator in order to maintain the post-correlation signal-to-noise ratio (SNR) of a correlation peak beneath a given threshold.
Our results provide a first estimate of the noise floor requirements for a receiver given a particular baseband implementation. Also, this study provides insight into the relationship between correlation time and performance degradation due to phase noise.
Phase Noise Model
Figure 1 (see inset, above right) shows the block diagram of a typical GNSS receiver considered for this study. Let us first consider the operation of the local oscillator (LO) in a receiver.
Any oscillator is defined by three parameters: phase (φ), amplitude (A), and frequency (f0). In a general case phase and amplitude noise exist, as well as distortion, which makes both A and φ functions of time.
. . .
Phase Noise and Code Correlation
Let us turn now to the factors involved in the effects of phase noise on code correction.
Post-Correlation Signal to Noise Ratio. Letting x(t) be an ideal real signal, having no quadrature component, we initially modulate a carrier at ω0 as x(t)·ejω0t.
. . .
During the correlation process in a GNSS receiver, this signal is multiplied by an ideal version of itself. Theoretically, when both are perfectly aligned the integral or area of the resulting function is maximized. Calculating the correlation over a period containing phase variations or even inversions results in an energy decrease, because part of the signal is subtracted rather than added (or the other way around should the correlation be negative).
. . .
As the accumulated phase shifts for a given noise level increase, the correlation time also increases. Thus, the integrated energy no longer increases linearly with time above certain phase noise levels, and eventually a point may be reached at which phase noise becomes dominant over post-correlation thermal noise, limiting the sensitivity increase one can obtain by increasing the correlation time. We present an explanation of this condition in the following section.
Mean Value of Correlation Peak. The average magnitude of the correlator output is calculated in order to estimate the noise and losses in the presence of phase noise. Instead of evaluating E[|Y|] we will address E[|Y|2] which provides a similar metric while still allowing an analytical approach.
. . .
In the frequency domain we can derive a theoretical expression for correlation losses using a free-running oscillator model in the RF front-end PLL. We assume that the PRN code is c(t). For the sake of simplicity, we also assume that noise and multipath effects are absent.
The complex PRN code correlation output R(τ) at the receiver is obtained by correlating the incoming down-converted signal with a local reference code delayed by τ seconds.
. . .
Correlation Noise. Signal losses due to phase variations during correlation already give the lower boundary for the phase noise specification. But this lower boundary alone does not represent the actual degradation of system performance.
It is reasonable to expect strong variations in the constellation (correlation noise) before the loss due to phase noise outweighs losses due to other factors in the receiver chain.
. . .
Model for Correlation Between Phase Noise and Pure PRN Codes
In the previous section describing the effect of phase noise on code correlation, we derived a relation between front-end oscillator phase noise and peak value of code correlation in the time and frequency domains, respectively. The next step is to prove this relation using a software-generated, simulation-based model of the code correlation process.
For this purpose, a numerical simulation program performed correlation between two versions of the same GPS PRN code. The first version was contaminated with various amounts of phase noise in order to replicate a real world PRN code received from the RF front-end and after the carrier strip-off process. The other version of the PRN code was kept ‘pure’ to mimic the local replica code as generated in every GNSS receiver.
. . .
Correlation Model for Noisy and Noiseless PRN Codes
The numerical model presented earlier simulates a stand-alone correlation process between noisy and noiseless PRN codes. However, none of the real-world GNSS receiver blocks nor their effects on the code correlation process were simulated.
For the next step, we correlate noisy and noiseless PRN codes using a datastream model for a Galileo receiver. We simulate both the code and carrier tracking loops to show the effect of phase noise while using a closed-loop code correlation process.
. . .
Results and Mathematical Interpretation
. . . As PNvariance increases, the mean and RMS of the correlation peak fall. The variance of the correlation peak increases up to a certain maximum and then also falls, but this decrease is in the region where the losses are already unsustainable. This result is reasonable, because the value of the correlation peak converges to zero.
Increasing the PIT above four milliseconds is also detrimental to the correlation output, because all the negative observations due to an increase in PNvariance begin at lower values of σ Φ2. In other words, the maximum allowable input PNvariance for a certain level of correlation peak RMS progressively decreases as we increase the PIT.
In the numerical and datastream simulations, an effective approach for identifying the maximum phase noise is to use a free-running local oscillator phase noise model, with a 10-decibel minimum correlation output SNR.
Although these boundaries for the SNR criteria seem very stringent, we plan to use more realistic, practical models in which phase noise flattens below a given frequency offset. We expect that this condition will, in turn, modify the slope of the SNR so that the synthesizer requirements would become closer to the figures offered by real receivers.
. . .
Conclusion
This phase model is a conservative first approximation, illustrating the relationships between phase noise, thermal noise, and correlator performance. In this article, we first presented an analytical approach for evaluating the effects of the local oscillator phase noise in the performance of the correlators of a GNSS receiver. A mathematical model validated the analytical approach, and a datastream model demonstrated the tracking channel imperfections based on GNSS receiver implementations
We characterized the relationship between the integration time and phase noise, and presented a criterion for radio front-end design. We believe this model offers new tools for the analytical design of GNSS receivers, while laying a conservative boundary for their practical design.
For the complete story, including figures, graphs, and images, please download the PDF of the article, above.
Acknowledgments
The research leading to these results has received funding from the European Community Seventh Framework Program (FP7/2007-2013) under grant agreement number 227890. This work has also been supported by the Academy of Finland.
Additional Resources
[1] Demir, A., “Phase Noise and Timing Jitter in Oscillators With Colored-Noise Sources,” IEEE Transactions on Circuits and Systems- Fundamental Theory and Application, Vol. 49, No. 12, December 2002
[2] Demir, A., and A. Mehrotra and J. Roychowdhury, “Phase Noise in Oscillators: a Unifying Theory and Numerical Methods for Characterization,” IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, Vol. 47, No 5, May 2000, pp. 655–674, DOI 10.1109/81.847872
[3] Hajimiri, A., and T. H. Lee, “A general theory of phase noise in electrical oscillators”, IEEE J. Solid-State Circuits, vol. 33, pp. 179-194, February 1998
[4] Irsigler, M., and B. Eissfeller, “PLL Tracking Performance in the Presence of Oscillator Phase Noise,” GPS Solutions, Volume 5(4), pp. 45-57, Spring 2002
[5] Kundert, K., “Predicting the Phase Noise and Jitter of PLL-Based Frequency Synthesizers,”, The Designer’s Guide Community <www- designers-guide.org>, Designer’s Guide Consulting Inc., August 2006
[6] Leeson, D.B., “Simple model of feedback oscillator noise spectrum,” Proceedings IEEE, p.369, February 1966
[7] Petovello, M., and E. Falletti, M. Pini, and L. Presti, “Are Carrier-to-Noise Algorithms Equivalent in All Situations?” GNSS Solutions, Inside GNSS, pp. 20-27, January/February 2010
[8] Petrovic, D., and W. Rave and G. Fettweis, “Effects of Phase Noise on OFDM Systems With and Without PLL: Characterization and Compensation,” IEEE Transactions on Communications, Vol. 55, No. 8, Aug 2007
[9] Rebeyrol, E., and C. Macabiau, L. Ries, J-L. Issler, M. Bousquet, and M-L. Boucheret, “Phase Noise in GNSS Transmission/Reception System,” Proceedings of the 2006 National Technical Meeting of the Institute of Navigation, January 18–20, 2006, Monterey, California, USA
[10] Sauvage, G., “Phase Noise in Oscillators: A Mathematical Analysis of Leeson’s Model,” IEEE Transactions on Instrumentation and Measurement, Vol. IM-26, No. 4, December 1977
[11] Schenk, T., “Phase Noise,” Chapter 4 of RF Imperfections in High-rate Wireless Systems, ISBN: 978-1-4020-6902-4, Springer 2008
[12] Schenk, T. (2006), “RF Impairments in Multiple Antenna OFDM – Influence and Mitigation,” Ph.D. Thesis, Technical University of Eindhoven, November 2006
[13] Syrjälä, V. and M. Valkama, “Analysis and mitigation of phase noise and sampling jitter in OFDM radio receivers,” European Microwave Association, International Journal of Microwave and Wireless Technologies, vol. 2, pp. 193-202, April 2010
[14] Syrjälä, V., and M. Valkama, N. N. Tchamov, and J. Rinne, “Phase Noise Modelling and Mitigation Techniques in OFDM Communication Systems,” Wireless Telecommunication Symposium, WTS 2009, April 2009, pp.1-7





