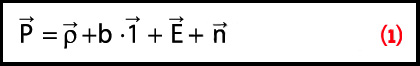FIGURE 1: Touching wavelet spectraFor the complete story, including figures, graphs, and images, please download the PDF of the article, above.
The use of GNSS for safety critical applications is gaining interest, particularly amongst aviation users, who probably have the most demanding requirements. The GNSS frequency band containing the Galileo E5 and GPS L5 signals is designated as an aeronautical radio navigation service (ARNS) band, which enjoys legal protection from other services not allocated to this frequency on a primary basis.
For the complete story, including figures, graphs, and images, please download the PDF of the article, above.
The use of GNSS for safety critical applications is gaining interest, particularly amongst aviation users, who probably have the most demanding requirements. The GNSS frequency band containing the Galileo E5 and GPS L5 signals is designated as an aeronautical radio navigation service (ARNS) band, which enjoys legal protection from other services not allocated to this frequency on a primary basis.
However, GNSSes do not hold exclusive rights to this frequency, and its use of the frequency on a primary basis may expose a GNSS signal to potential interference from other services that enjoy similar emission rights, affecting performance in safety critical applications.
These other services include pulsed interference originating from systems such as distance measuring equipment (DME), Tactical Air Navigation (TACAN) signals, and the Joint Tactical Information Distribution System (JTIDS), as well as military radars that may cause significant service degradation. Moreover, in addition to the severe effects on the E5/L5 band by induced interference, the situation becomes even more problematical when these signals are used in conjunction with the Galileo E6 frequency band.
Not only pulsed interference, but also other RF transmissions such as continuous wave (CW) signals can degrade the reception of GNSS signals. An example of such interference occurs due to the harmonics originating from the European digital video broadcast terrestrial (DVB-T) service, which can appear in RNSS frequency bands.
Interference can be mitigated through various means. On the hardware side, specialized instrumentation such as choke rings or active beam-forming antennas, suppress interference and improve the reception of line-of-sight satellite signals. Special RF front-end architectures make use of pulse blanker and/or automatic gain control (AGC) to reduce RFI. With respect to a GNSS receiver’s digital signal processor (DSP), performance degradation due to interference can be treated in the receiver’s software, using interference mitigation algorithms.
In this column, we will focus on the DSP solutions, although we need to emphasize that in order to achieve the best results, all three elements of a generic GNSS receiver antenna, RF front-end, and DSP — must be considered, while measures taken for any individual element need to be coordinated with the others.
Interference Mitigation by Means of Wavelet
Pulse blanking is the most common approach to suppress pulsed interference. However, some traditional pulse blanking designs are based on monitoring the automatic gain control (AGC) within the receiver’s front-end and activating the blanking at instances when an abrupt and significant increase of the AGC is reported. Due to the limited dynamics of the AGC, pulse blanking suffers is less effective in cases where high pulse repetition frequencies occur.
The wavelet based technique described in detail by C. Burrus et alia in the publication cited in the Additional Resources section near the end of this article is not based on AGC techniques. Thus, it is not only suited for high power pulses but also for medium to low power pulses, as we will demonstrate later on. Further benefits of the wavelet approach to interference mitigation for pulsed interference are explained in the article by E. Anyaegbu et alia (see Additional Resources) in the frame of GNSS signal processing.
The traditional Fourier series and fast Fourier transformation (FFT) are based on sinusoidal functions with infinite support. Although applying this transformation gives complete insight into the signal’s frequency evolution, it removes all time-dependent information that we might want to analyze.
An analysis of pulsed interference requires both a time and frequency representation of the signal. To achieve this end, we could cut the signal into several time-dependent sections and then analyze each independently. However, we still need to determine the instant in time to cut the signal, while identifying all frequency components at a certain time instance.
In order to meet this desire, we cut the signal using a Dirac pulse and then transform the result to the frequency domain. The cutting of the signal corresponds to a convolution in the time domain and thus to a multiplication in the frequency domain. Finally, a Fourier transform of the Dirac pulse contains all possible frequencies and consequently the frequency information of the initial signal is smeared out to all frequencies.
This concept is an analogous to Heisenberg’s uncertainty relation as — in signal processing terms — it is impossible to know the exact frequency and the exact time resolution of a signal. The key to analyzing pulsed interference can be seen in the selection of the correct cutting of the signal.
With wavelet analysis we overcome this problem by selecting the time at which to cut the signal using a flexible and scalable window function. We shift the window along the time axis for every point in time the spectrum is calculated, which can be repeated several times using slightly compressed window functions.
The final result is a time-frequency representation of the signal. In the wavelet analysis the frequency term is mostly replaced, as explained later, by a scaling operation to have a clear boundary to the Fourier transformation.
Continuous Wavelet Transformation
. . . The wavelet functions are deduced from one single wavelet, the so-called mother wavelet ψ(t), by scaling and translation . . . These formulas are not linked to a unique and single function ψ(t) as with the case for the Fourier transformation. We declare functions for which a number of characteristic properties hold as “mother wavelets.” We invite interested readers to consult Burrus et alia for a further explanation of wavelet mother functions.
Discrete Wavelet Transformation
Working with sampled data requires the definition of a discrete Wavelet Transformation…Discrete wavelets require an infinite number of scalings and translations in order to be able to fully represent the original input function. Although a break-off of the wavelet series may offer a way out, the truncation error still needs to be controlled.
From the defining characteristics of a wavelet function, we suggest that Wavelet functions offer a band-pass–like spectrum, where a compression in time can also be expressed as a stretch in the frequency domain together with a shifting up to higher frequencies.
We use this characteristic to construct a series of wavelets covering the whole frequency range of our input signal, where special attention needs to be paid so that each stretched wavelet spectra touch its neighbors as shown in Figure 1 (see inset photo, above right).
In practice, it is impossible to cover all spectrum of an input function down to zero. The most elegant solution resulting in applicable wavelets is to stop stretching the wavelet once the open hole is small enough and then fill it with a so-called scaling function.
. . .
Pulsed Interference Mitigation by Wavelets
Now that we have defined the prerequisites for Wavelet analyses, we would like to return to our original approach to identifying and mitigating medium to low pulsed interference by means of wavelets.
. . .
Step 1 — Discrete Wavelet Transformation. The first step towards correctly identifying pulsed interference uses a discrete wavelet transformation, with a complete manifold of potential wavelet mother functions. For the best results — that is, those yielding both the highest correlation between the pulsed interference and the wavelet, as well as the lowest correlation between the wavelet function and the GNSS plus noise signal — an optimization could be carried out …
Step 2 – Exact Pulse Position in Time. With appropriate knowledge of the expected pulse duration, a constant windowing function g(t) is generated and correlated with the approximate scale coefficients. This determines the correct time location of the pulse within the IF samples … where an easily distinguishable local maximum is obtained in the pulse-present case …
Step 3 – Pulsed Interference Excision. After correct identification of the pulse in the time domain, we perform a pulse excision by modifying the affected approximate and detailed scale coefficients, cA and cD. After comparing potential solutions by modifying the scale coefficients, the classical blanking approach still shows best performance.
Step 4 – Inverse Discrete Wavelet Transformation. In the final step, we apply an inverse discrete wavelet transformation in order to regain the original IF samples after eliminating the samples affected by pulsed interference.
Low Power DME Interference Mitigation
Distance measuring equipment employs a transponder-based radio navigation technology that measures distance by timing the propagation delay of radio signals. DME pulsed interference is to be expected in the 1151–1213 megahertz frequency range when operating in X mode, thus affecting the E5/L5 band.
. . . While the wavelet-based interference mitigation approach has been outlined earlier for high-power pulses, here, we assess the performance of these algorithms for the case of low-power interference. We use a standard pulse interval of 12 microseconds between the two DME single pulses, while we consider a repetition rate of about 2,700 pulse pairs per second (pps) at the upper limit of the DME specifications.
. . .
Performance Assessment of Wavelet-Based Interference Mitigation
Now that we have demonstrated the capability of wavelet techniques to detect interference, we will apply the mitigation approach and assess its performance. We evaluate the mitigation approach, for both the case of the high-power pulsed interference scenario as well as for low-power DME pulsed interference.
. . .
Wavelet-Based Interference Mitigation vs. Pulse Blanking
We compared the benefits and drawbacks of the well-established time domain pulse blanking technique with the wavelet-based approach for mitigating pulsed interference.
. . .
Summary of Wavelet-Based Interference Mitigation
We consider signal analysis by means of wavelets as an innovative technique, providing not only insight into the frequency content of the signal as with the traditional Fourier analysis but also enabling signal analysis in the time domain.
. . .
Notch Filtering for CW Interference Mitigation
The design of interference mitigation algorithms applicable to continuous wave (CW) interference focuses on suppression of the high spectral peaks related to the interferer.
. . .
Performance Assessment of Notch Filtering–Based Mitigation Technique
… After applying the notch filter, the spectral peaks originating from the CW interference were well suppressed. The resulting PSD is almost identical to the one without any interference.
. . .
Conclusion and Future Developments
We have outlined two different interference mitigation approaches, applied to the digital part of GNSS receivers. Wavelet-based pulsed interference mitigation shows a significant potential for future use for both high- and low-power pulses, enabling accurate detection and mitigation. Significant performance improvements are measured at both the C/N0 level and tracking loop level have been reported for high power pulsed interference.
Additionally, our analysis of notch filtering against CW interference threats indicates significant capabilities as well.
We should underline that all algorithms have been implemented in the IpexSR software receiver, enabling interference mitigation in a post-processing laboratory environment. Currently, implementation of the wavelet-based interference mitigation approach for real-time applications in particular is being pursued at the University FAF Munich Institute of Geodesy and Navigation.
For the complete story, including figures, graphs, and images, please download the PDF of the article, above.
Acknowledgment
The results shown in this paper have been accomplished at the Institute of Geodesy and Navigation of the University FAF Munich within ESA contract No. 21095/07/NL/HE.
Additional Resources
[1] Anyaegbu, E., and G. Brodin, J, Cooper, E, Aguado, and S. Boussakta, “An Integrated Pulsed Interference Mitigation for GNSS Receivers,” Journal of Navigation, The Royal Institute of Navigation, Cambridge University Press, Volume 61, Issue 2, 2008
[2] Burrus, C.S., and R. A. Gopinath and H. Guo, Introduction to Wavelets and Wavelet Transforms: A Primer, Prentice Hall, Upper Saddle River, New Jersey, USA, 1998
[3] ICAO NSP WG1&2/WP5: Interference Susceptibilities of Aeronautical Systems Operating in the 960-1215 MHz Band, 2005
[4] Steingass, A., and A. Hornbostel and H. Denks, “Airborne Measurements of DME Interferers at the European Hotspot,” Proceedings of European Navigation Conference ENC/GNSS 2009, Naples, Italy, May 04, 2009
[5] Stöber, C., and M. Anghileri, A. Sicramaz Ayaz, D. Dötterböck, I. Krämer, V. Kropp, J.H. Won, B. Eissfeller, D. Sandromà Güixens, and T. Pany, “IpexSR: A Real-Time Multi-Frequency Software GNSS Receiver,” Proceedings of IEEE ELMAR 2010, Zadar, Croatia
