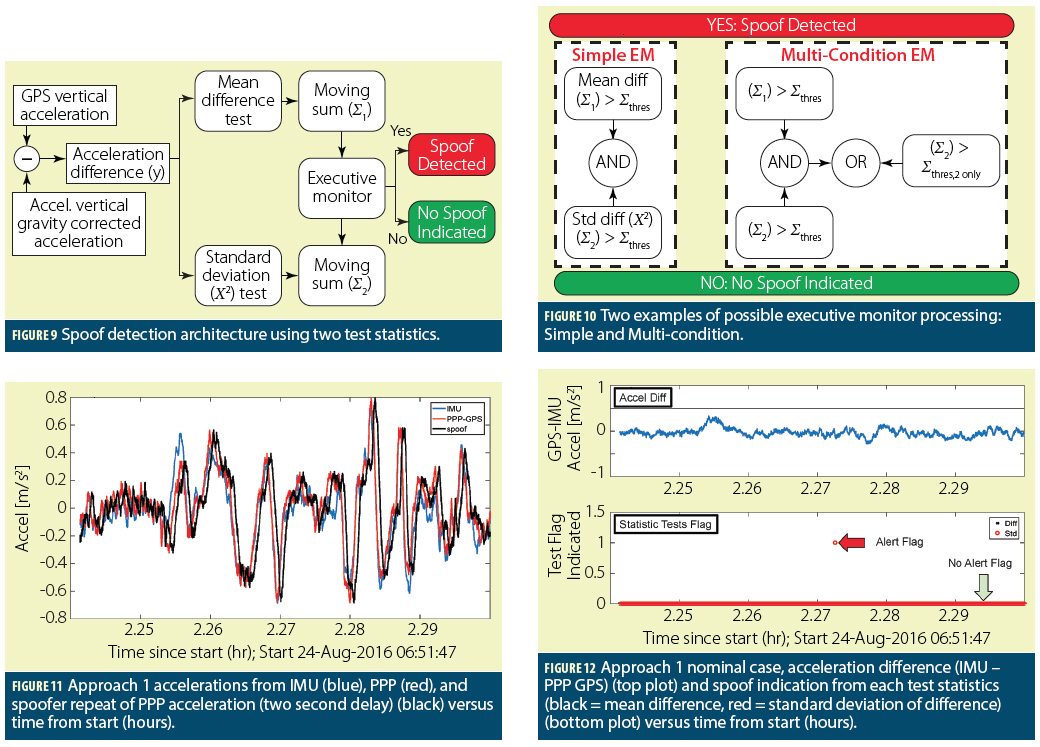
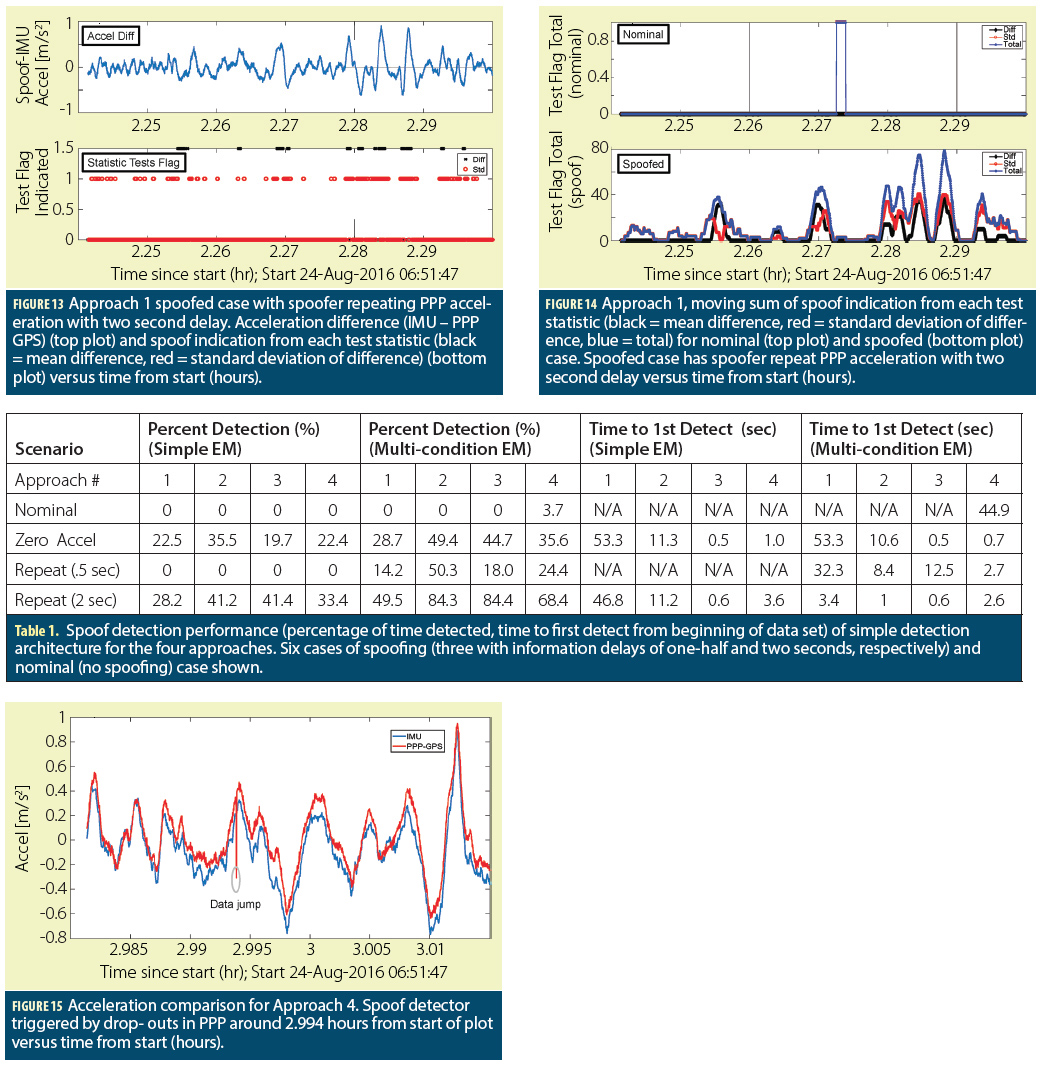
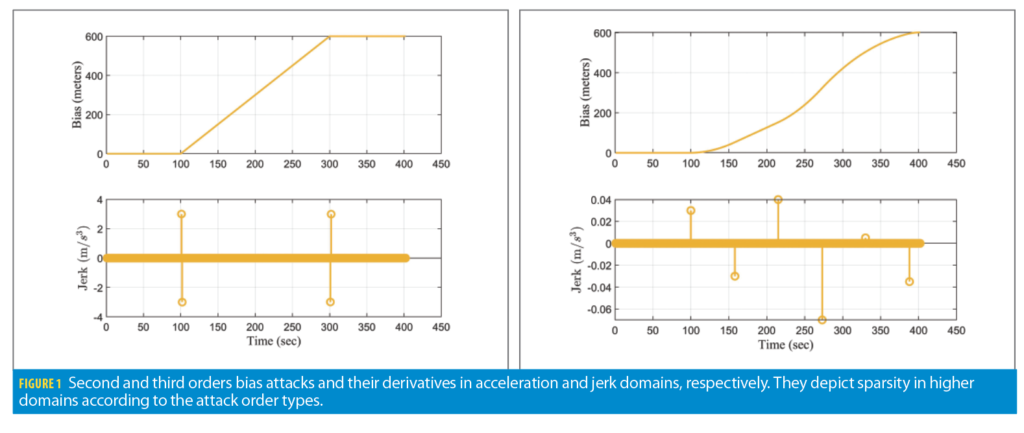
Verifying spoofing countermeasures based on sparse signal processing.
JUNHWAN LEE, ERICK SCHMIDT, NIKOLAOS GATSIS, DAVID AKOPIAN
UNIVERSITY OF TEXAS AT SAN ANTONIO
Global Navigation Satellite Systems (GNSS) offer an irreplaceable service on providing Position, Velocity and Time (PVT) references for various applications. The growing reliance on GNSS has generated increased interest on its authentication, validity and security, which is undeniably challenging due to external interference. Inherently, the GNSS receiver is susceptible to experiencing a range of disturbances during long-distance satellite-to-receiver communication. The GNSS receiver can thus become a victim of a harmful third-party hacker, a situation the relevant literature shows is applicable and plausible [1],[2].
Major cybersecurity attacks against GNSS receivers include jamming and spoofing. While blocking one or more satellite channels, jamming attacks force the receiver tracking loop to be locked on a false high-powered correlation peak. Spoofing, often referred to as a smart attack, hijacks tracking correlation peaks with matched-power noise to create deviations in PVT solutions. Carefully designed spoofing attacks can bypass basic Receiver Autonomous Integrity Monitoring (RAIM ) detection mechanisms. This article outlines a framework that defines various types of spoofing attacks based on their sparsity characteristics and leverages the aforementioned properties toward showcasing and verifying spoofing countermeasures.
Smart grid, an infrastructure that has significant reliance on timing synchronization via GPS, is a vulnerable target for malicious spoofing actors. In the work of [3], scenarios where time synchronization attacks (TSAs) lead to failures in power system state estimation are illustrated, which may eventually cause failure to take a corrective action. Another significant application that has attracted prominent research and heavily hinges upon the position and velocity estimations of GNSS receivers is unmanned autonomous vehicle (UAV) navigation. The spatial spoofing research is rich in analyzing attack mechanisms, whose effects are chiefly showcased on UAVs or other vehicles [2],[4].
As much as the dangers of spoofing are manifested through research work, a plethora of publications attempt to introduce promising antispoofing countermeasures [5],[6]. In general, antispoofing countermeasures may offer two fundamental features. Initially, the algorithm captures abnormal behavior discovered during either baseband or signal-level search. The aforementioned process is commonly referred to as detection. Several mechanisms halt their mission once spoofing detection is attained. Mitigation goes beyond detection in that it rejects the attack signal and produces accurate PVT estimates.
Among the methodologies available in the literature, several target the baseband domain and strive to capture unpredictable or abnormal behaviors of any sort. More specifically, the relevant research often uses the observable changes on correlator peaks [7],[8], vector tracking loops [9] or power and automatic gain control [10],[11]. Such research sometimes requires supplementary circuitry to be included in off-the-shelf receivers or has to rely on one or more sophisticated receivers.
On the other hand, certain antispoofing techniques focus on the signal-level layer of the GPS receiver. These techniques strive to detect anomalies in observable sequences such as carrier-to-noise ratio [12], and navigational drift [13],[14]. This article falls in the latter category and exploits common GPS observables, that is, pseudorange and pseudorange rate as a pair, to protect the receiver against malicious spoofing. Moreover, the presented algorithm is cost-effective; it can run on a single rudimentary receiver assisted with software routines such as the freely deployed Android software.
This article presents the basics of an algorithm that is capable of autonomous spoofing detection and mitigation of joint attacks against time and position. Specifically, the present work focuses on stationary receivers and, with respect to the position attack, it provides an effective method to capture and reject an attack against a single position coordinate. The developed model expands on our previous work [15] that deals with TSAs only.
GPS Observable Pair
The fundamental GPS observables we used to contrive the antispoofing mechanism are the pseudorange and pseudorange rate pair. These data are typically accessible in mobile phones, for example, with certain applications installed as well as off-the-shelf commercial receivers. This section briefly discusses the observable pair and how the PVT excursion is arranged.
Pseudorange (ρn) refers to the computed satellite-to-receiver distance. The satellite and user position are respectively denoted by pn=[xn yn zn ]T and user position pu=[xu yu zu ]T where n = 1,2,…,N refers to the total number of tracking satellites represented in Earth-Centered Earth-Fixed (ECEF) coordinates. The 3-dimensional Euclidean norm based on the difference in satellite-to-receiver positions can generate the true range of the user, which, however, differs from observed pseudorange reported by the receiver due to the induced clock biases at the satellite and user ends, respectively denoted by bn and bu.
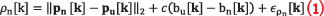
where c represents the speed of light, and any Gaussian white noise is captured in .
A complementary component in the measurement pair is Doppler rate, or alternatively referred to as the pseudorange rate. Caused by the effect of Doppler shift that is generated between maneuvering satellites and the receiver, the pseudorange rate must satisfy the following consistency requirement:

where satellite n’s velocity is referred to as vn= and the velocity of the receiver as vu=
. During satellite-to-receiver data communication, the user readily obtains information in regard to all the visible satellites such as position (pn), velocity (vn), and clock offset and bias (
and
), which in turn leaves user PVT variables (pu, vu, bu, and
) as unknown.
Once measurement data was fully captured on the receiver, we performed a sanity check examination using Equation 2 to attain the validity of acquired data. The pair of pseudorange and pseudorange rate equations needs to be linearized for two reasons. The user position pu in Equation 1 is under the Euclidean norm, which is a nonlinear function. Also, considering pseudorange rate equation, though not stated in this article, includes the user velocity under the Euclidean norm as well.
Although general-purpose nonlinear programming (NLP) solvers are available, a linearized model can leverage the computational advantages of convex optimization solvers, namely rapidly calculating PVT solutions, without losing accuracy. The linearization is performed using Taylor series expansion. Because the present work is concerned with stationary receivers, the observed pair are linearized with respect to a fixed known user position reference, pu.ref, and zero velocity reference vu= 0. See [17] for a detailed derivation of the linearization. To clarify the observed model versus linearized pair, we refer to linearized pseudorange and pseudorange rate as and
.
In the presence of spoofing, injected attacks are modeled as additive to the measurement pair. The following equations manifest the representation of spoofed pseudorange and pseudorange rate:

where and
represent spoofing signals injected on pseudorange and pseudorange rate, respectively. The attacked pseudoranges and pseudorange rates are conventionally provided as inputs to traditional algorithms such as Weighted Least Squares (WLS) or extended Kalman Filter (EKF), which output the PVT solutions to the end user. Thus, the abnormal behavior captured in pseudoranges is transferred on the PVT solutions.
Spoofing Attack Order
In our previous work [15], we specifically consider TSAs and examine whether higher-order discrete-time derivatives of the spoofing signal are sparse, that is, exhibit spike-like behavior. This article extends the premise to attacks against a single position coordinate, and we specifically focus on the z coordinate in ECEF domain. Following [15], we analyze the smallest order derivative where the attack exhibits evident spikes and define the attack accordingly. For instance, a so-called Type I attack in [13] can be re-identified as a first order attack for the sparsity occurs in velocity domain, or equivalently in the first derivative of position.
Considering the bias domain, we define second order and third order attacks with examples depicted in Figure 1. The second order attack with increasing trend is shown in Figure 1a, whose second derivative (the acceleration) features two spikes at 100 and 300 seconds. Figure 1b depicts subtle gradual changes akin to third order attack where the sparsity is achieved on the third derivative (jerk domain). The chief advantage in defining spoofing profiles to benefit the development of antispoofing models is the fact that sparsity appears on the jerk domain for the majority of attacks reported in the literature.
Spoofing Consistency
Attack consistency is inspired by the measurement integrity in Equation 2. Applying the rationale to the spoofing signal, a consistent attack is required to satisfy the following condition:
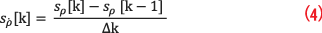
If the attacks fail to satisfy (4), it can be referred to as a non-consistent attack. An example of a consistent attack is TSA [13]. While fulfilling measurement integrity, deviating signals on psuedorange and pseudorange rate are explicitly manifested on clock bias and drift. Particular applications vulnerable to TSAs are electric power grid operations that are driven by Phasor Measurement Unit (PMU) readings. PMUs are equipped with (stationary) GPS receivers, whose timing errors translate into voltage and current phase angle deviations. These can subsequently lead to erroneous state estimation for the power grid [20]. The authentic spoofing database TEXBAT corroborates the aforementioned TSA characteristics, which also can be incited with baseband spikes.
In case of spatial spoofing, the attack may be defined as consistent or non-consistent depending on the targeted domain. If the spoofer aims to solely vary a position estimate and leaves the velocity domain intact, that would be an example of a non-consistent attack. Consistent spatial attacks result in modification on position and velocity domains.
This article considers attacks against two domains: TSA (clock bias b) and single-coordinate position (coordinate z), whereby time and spatial solutions are simultaneously affected. This condition is called a joint attack. In practical applications, such complicated spoofing can be achieved by having the receiver hacked by different data sources [21]. For joint attack simulation, we only examine consistent attack because TSA must be applied with the spoofing integrity.
GPS Dynamic Equations
The GPS receiver is described by a dynamical system that follows the random walk model [16]:

where xk stands for state variable vector, Fk is the state transition matrix, and wk refers to the state transition noise. Although in a stationary environment, the position does not vary and the velocities in x, y, z remain zero, Equation 5 is adopted in the present work because xk may contain deviating signals, and specifically, attacks that modify the solution in the b or z domains. Including the unknown xk as an optimization variable may be beneficial toward recovering the authentic PVT solution. Further, as mentioned earlier, the spoofing signal variables are appended for the system to delineate authentic PVT solutions with inflicting signals, with linearized measurement vectors zk=[zρ zρ⋅]T, which can be expressed as the following:

in which sk place-holds captured deviating signals introduced on z-position (sz), velocity, (sz⋅), clock bias (sb) and drift (sb⋅). Such formulation aims to capture the attack introduced onto the clock timing and z-domain. Lastly, represents the zero mean Gaussian measurement noise with covariance matrix Rk=diag
that can determine uncertainties of observed measurements.
Proposed Anti-Spoofing Technique
The proposed anti-spoofing technique is based on a minimization formulation that lends robustness against the spoofing attacks described earlier. The following minimization is performed as solver estimates ,
:
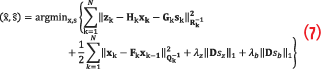
Equation 7 consists of four objectives that serve the anti-spoofing scheme. The first summation term is derived from the measurement in Equation 6. The second term examines the PVT behaviors in relation to the random walk model. The third and fourth terms, nominally referred to as penalization functions, each represent the higher-order domain where sparse spikes are likely to be displayed in position and clock aspects, respectively. The first and second terms jointly encourage PVT solutions that satisfy measurement integrity. With the help of penalization terms, the technique is capable of filtering accurate PVT estimations against attacks. The matrix D constructs the third-order derivative of the respective sequences and is defined as follows:

The selection hinges upon the observation that realistic spoofing typically exhibits sparsity in the third-order derivative domain (jerk).
The performance of the technique depends on the selection of the factors λz and λb. These must be selected for each receiver. The proper values of λz and λb can tune the level of sparsity that emerges as solution from (7), as well as the relative emphasis that is placed among the four objectives in Equation 9. Proper tuning based on realistic attacks and in representative environments is therefore recommended.
Another parameter that affects the quality of the solution is the state noise covariance matrix. This must be set up with appropriate values corresponding to the static receiver. Overall, the optimization problem in (9) is a convex quadratic program that can be solved with relatively small computational effort.
Simulation Methodology
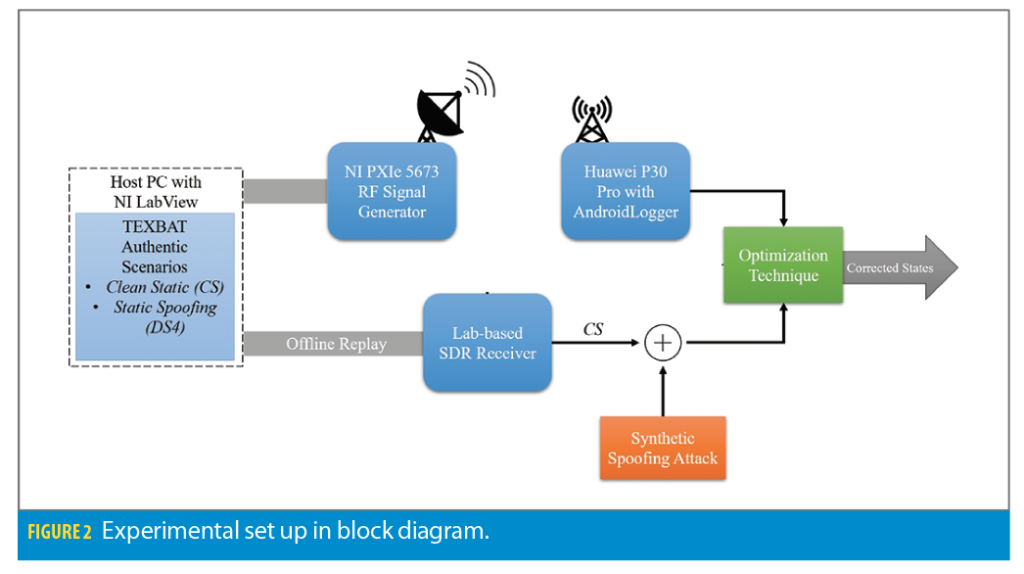
To simulate and visualize the malignant effect of various spoofing types, we use a GPS receiver testbed that incorporates the wired and wireless signal transmission and reception simulations. We transmit a pre-recorded GPS signal via signal generator, namely Clean Static (CS) scenario from TEXBAT database [1]. Interfaced with LabView developed software along with PCIe, the GPS signal transmitter uses a NI PXIe-1075 Chassis with a PXIe 5673 RF Signal Generator broadcasting via Vert 900 antenna.
Once transmitter setup is complete, the user has two choices as per the simulation. The unprocessed data is directly fed into the wired Software Defined Radio (SDR) developed in our lab [22], which rapidly processes the raw data into precise and comprehensible GPS information for the user. On the other hand, users can opt to deliver the signal over-the-air (OTA) via the connected antenna, in which the Huawei receiver, located about 5 to 6 meters away from the transmitter, captures and processes the signal with the GNSSLogger application [23].
The wireless route inherently contains more noise and consequently has higher uncertainties than the wired method. Thus, wired SDR empowers the PVT processing algorithms such as WLS and EKF to deliver more accurate position and time estimation. In this article, we exploit synthetically fabricated spoofing attacks while targeting a single position and time domain, namely z-domain in ECEF coordinate and clock bias estimation.
The attacks described next are synthetically added to the output of the TEXBAT CS scenario after it is replayed over the SDR and the Huwaei receiver. We initially confirm our algorithm attains robustness against TSA in various spoofing profiles as our previous works do [15], then simulation manifests the algorithm also can detect and mitigate the disturbance that aims to inflict 1) sole z-domain and 2) z-domain and clock bias simultaneously.
Each spoofing scenario is comprised of first, second and third order types of attacks while maintaining a minimum of 600 meters of deviation. The routines processing raw measurements that are reported from two receiver test beds, as well as PVT acquisition algorithms, namely, WLS, EKF and our algorithm, are all written in MATLAB. The MATLAB-friendly convex optimization modeling software, cvx, is used to solve the quadratic program in the novel algorithm, and is employed in the effort to estimate the correct PVT solution and the spoofing attack.
Numerical Results
This section reports and examines the output of synthetic attack simulations. Both the SDR and the Huawei commercial receiver accumulate the TEXBAT clean static data, and we added the tailored spoofing scenarios onto the processed pseudorange pair. Multiple figures depict the outstanding performance of our algorithm, numerically compared by using Root-Mean-Sqaure-Error (RMSE) values against the estimation produced by EKF. The following equation defines the RMSE for the z-coordinate:

Scenario 1: TSA
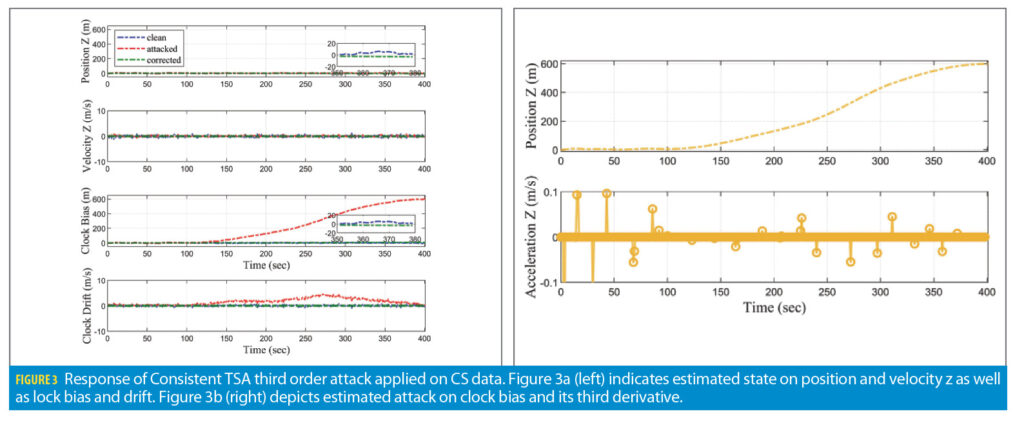
Figure 3 shows the result of sole TSA spoofing on the SDR receiver. A total of 600 meter magnitude deviation is applied to the clock bias; the drift changes accordingly. The third order spoofing profile has the smoothest shape that can have numerous sparse spikes on the jerk domain. Based on the consistency characteristic of TSA, the deviating shape and magnitude applied on clock bias are exactly identical to modifying signals on psuedoranges. Though the spoofing setting is identical to the experience executed in the work of [15], the algorithm based on the minimization of (7) differs from the approach shown in aforementioned paper.
The primary task of third component in (7) is to filter the estimated attack from the correct PVT solution, xk. We select λb=10. The optimization problem acknowledges the abnormal behavior on the bias domain, also by expecting subtle sparse peaks on jerk. Figure 3a shows the clean (WLS output), attacked (EKF output) and corrected (optimization output) of z position, velocity, clock bias and drift estimations. As Figure 3a suggests, the corrected solutions all maintained to be less than absolute 20 meters. Further, the RMSE error on z coordinate is reduced from 389.22 meters to 2.25 meters. Figure 3b depicts the estimated attack, which turns out to be similar to the applied attack.
Scenario 2: Spatial Spoofing
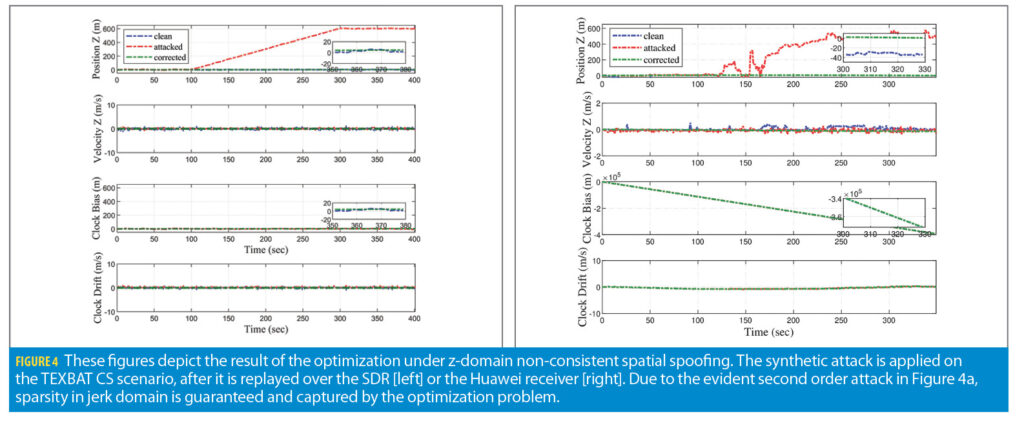
The second scenario explores the second order spatial spoofing where only the position estimate is affected by the pseudorange deviation. The deviating magnitude gradually increases from 100 to 300 seconds with ultimate amplitude of 600 meters. The second order spoofing profile expects to show peaks in acceleration and jerk domains. The major improvement made with respect to our previous approach [15] is attaining robustness against spatial spoofing. Due to measurement linearization, our algorithm has the capability to search more than clock domain.
The plots in Figure 3 express the result of sole spatial spoofing in z-domain, namely the result of the optimization after applying the synthetic attack to the replayed CS scenario over the SDR and the Huawei receiver. Even though the Huawei recordings in Figure 4b have more noise than the SDR recordings shown in Figure 4a, both cases successfully captured and mitigated the attack using a tuning parameter of λz=10. Further, the RMSE value for the z domain in the SDR case reduced from 389.22 meters to 6.03 meters; and the corresponding one for the Huawei receiver decreased from 357.37 meters to 32.77 meters. Other variables produced by the optimization such as z-velocity, clock bias, and drift, are estimated very closely to the ground truth.
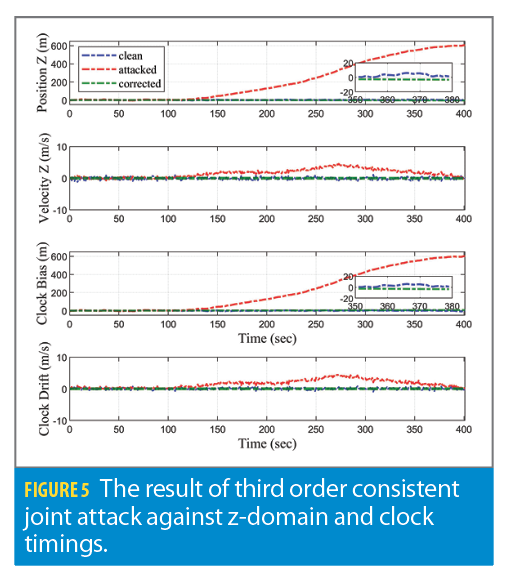
Scenario 3: Joint Attack
The third spoofing scenario for a stationary receiver is the joint TSA and spatial attack. Because TSA is supposed to be a consistent attack, we simulate an overall consistent joint attack with 600 meters maximum magnitude and third-order profile. The joint spoofing was only able to be rejected upon tuning of the penalization terms. Figure 5 indicates the algorithm successfully mitigates the attack on any domains of search. The RMSE value also has been reduced similarly to Scenarios 1 and 2. This manifests that the developed algorithm can deny any type of spoofing attack whether it targets singular or multiple domains.
Conclusion and Summary
This article develops a technique to mitigate joint spoofing against time and a single position coordinate in stationary GPS receivers. To this end, a suitable linearization of the GPS measurement equation is presented and sparsity characteristics of attacks are reviewed. The technique relies on minimization of a multi-criterion objective that includes penalization giving rise to sparse solutions. Three synthetic spoofing scenarios are successfully mitigated. The resulting RMSE values in each scenario are reduced significantly versus the EKF estimations, meanwhile the absolute error is small as well. Our current work [17] focuses on expanding the model to receivers with slow dynamics, successful mitigation of joint attacks an all PVT domains analyzing the effects of different attack orders and degrees of consistency, and validation with authentic spoofed signals from the TEXBAT database, as opposed to synthetic attacks only.
Acknowledgements
This article is based on material presented in a technical paper at ION GNSS+ 2021, available at ion.org/publications/order-publications.cfm.
This material is based upon work supported by the National Science Foundation under Grant No. 171904.
References
(1) . E. Humphreys, J. A. Bhatti, D. P. Shepard, and K. D. Wesson, “The Texas Spoofing Test Battery: Toward a Standard for Evaluating GPS Signal Authentication Techniques,” Proc. of the 25th Int. Tech. Meeting of the Sat. Div. of The Inst. Of Nav. (ION GNSS 2012), p. 3569–3583, Nashville,TN, September 17–21 2012.
(2) . P. Shepard, J. A. Bhatti, T. E. Humphreys, and A. A. Fansler, “Evaluation of Smart Grid and Civilian UAV Vulnerability to GPS Spoofing Attacks,” in Proc. 25th Int. Tech. Meeting of the Sat. Div. of The Inst. of Nav. (ION GNSS), Nashville, TN, Sept. 2012, pp. 3591–3605.
(3) . Risbud, N. Gatsis, and A. Taha, “Vulnerability Analysis of Smart Grids to GPS Spoofing,” IEEE Transactions on Smart Grid, vol. 10, no. 4, pp. 3535–3548, 2019.
(4) . Ma, J. Yang, J. Chen, Z. Qu, and C. Zhou, “Effects of a Navigation Spoofing Signal on a Receiver Loop and a UAV Spoofing Approach,” GPS Solutions, vol. 24, 05 2020.
(5) . L. Psiaki and T. E. Humphreys, “GNSS Spoofing and Detection,” Proceedings of the IEEE, vol. 104, no. 6, pp. 1258–1270, June 2016.
(6) . Broumandan, A. Jafarnia-Jahromi, S. Daneshmand, and G. Lachapelle, “Overview of Spatial Processing Approaches for GNSS Structural Interference Detection and Mitigation,” Proceedings of the IEEE, vol. 104, no. 6, pp. 1246–1257, 2016.
(7) . Schmidt, N. Gatsis, and D. Akopian, “A GPS Spoofing Detection and Classification Correlator-Based Technique Using the LASSO,” IEEE Trans. on Aero. and Elect. Systems, vol. 56, no. 6, pp. 4224–4237, 2020.
(8) . Wang, H. Li, and M. Lu, “GNSS Spoofing Detection and Mitigation Based on Maximum Likelihood Estimation,” Sensors, vol. 17, June 2017.
(9) . Xu, Q. Jia, and L.-T. Hsu, “Vector Tracking Loop-Based GNSS NLOS Detection and Correction: Algorithm Design and Performance Analysis,” IEEE Trans. on Instrum. and Meas., vol. 69, no. 7, pp. 4604–4619, 2020.
(10) . D. Wesson, J. N. Gross, T. E. Humphreys, and B. L. Evans, “GNSS Signal Authentication Via Power and Distortion Monitoring,” IEEE Trans. on Aero. and Elect. Systems, vol. 54, no. 2, pp. 739–754, 2018.
(11) . Broumandan, A. Jafarnia-Jahromi, and G. Lachapelle, “Spoofing Detection, Classification and Cancelation (SDCC) Receiver Architecture for a Moving GNSS Receiver,” GPS Solutions, vol. 19, pp. 475–487, 2014.
(12) . D. J. Nielsen and G. Lachapelle., “Effectiveness of GNSS Spoofing Countermeasure Based on Receiver CNR Measurements,” Int. Journ. of Nav. and Obs., vol. 2012, 2012.
(13) . Khalajmehrabadi, N. Gatsis, D. Akopian, and A. F. Taha, “Real-Time Rejection and Mitigation of Time Synchronization Attacks on the Global Positioning System,” IEEE Trans. on Industrial Electronics, vol. 65, no. 8, pp. 6425–6435, 2018.
(14) . Lee, A. F. Taha, N. Gatsis, and D. Akopian, “Tuning-Free, Low Memory Robust Estimator to Mitigate GPS Spoofing Attacks,” IEEE Control Systems Letters, vol. 4, no. 1, pp. 145–150, 2020.
(15) . Schmidt, J. Lee, N. Gatsis, and D. Akopian, “Rejection of Smooth GPS Time Synchronization Attacks via Sparse Techniques,” IEEE Sensors Journal, vol. 21, no. 1, pp. 776–789, 2021.
(16) . Axelrad and R. G. Brown, “GPS Navigation Algorithms,” in Global Positioning System: Theory and Applications, B. W. Parkinson, J. J. Spilker, P. Axelrad, and P. Enge, Eds., 1996, vol. I, ch. 9.
(17) . Lee, E. Schmidt, N. Gatsis, and D. Akopian, “Detection and Mitigation of Spoofing Attacks Against Time Synchronization and Positioning,” submitted for publication, 2021.
(18) . Zhu, A. Youssef, and W. Hamouda, “Detection techniques for data-level spoofing in gps-based phasor measurement units,” in 2016 International Conference on Selected Topics in Mobile Wireless Networking (MoWNeT), 2016, pp. 1–8.
(19) . P. Shepard and T. E. Humphreys, “Characterization of Receiver Response to a Spoofing Attacks,” in Proceedings of the 24th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2011), Portland,OR, September 2011 2011, pp. 2608–2618.
(20) . Zhang, S. Gong, A. D. Dimitrovski, and H. Li, “Time Synchronization Attack in Smart Grid: Impact and Analysis,” IEEE Transactions on Smart Grid, vol. 4, no. 1, pp. 87–98, 2013.
(21) . Miralles, N. Levigne, D. Akos, J. Blanch, and S. Lo, “Android Raw GNSS Measurements as the New Anti-Spoofing and Anti-Jamming Solution,” in Proc. of the 31st Int. Tech. Meeting of the Sat. Div. of The Inst. of Nav. (ION GNSS+ 2018), Miami, Floridar, September 2018 2018, pp. 334–344.
(22) E. Schmidt, D. Akopian, and D. J. Pack, “Development of a Real-Time Software-Defined GPS Receiver in a LabVIEW- Based Instrumentation Environment,” IEEE Trans. on Inst. and Meas., vol. 67, no. 9, pp. 2082–2096, 2018.
(23) “Raw GNSS Measurements; Android Developers.” [Online]. Available: https://developer.android.com/guide/topics/sensors/gnss
Authors
Junhwan Lee received his B.S. degree in electrical engineering from the University of Texas at San Antonio (UTSA) in 2017. He is currently a Ph.D. candidate in the Department of Electrical and Computer Engineering at UTSA. His research interests include GNSS interference mitigation technique, state estimation in optimization and control theory.
Erick Schmidt received his B.S. degree in electrical engineering from Monterrey Institute of Technology and Higher Education, Monterrey, Mexico, in 2011 and both his M.S. and Ph.D. degrees in electrical engineering from The University of Texas at San Antonio (UTSA) in 2015 and 2020 respectively. His research interests include baseband processing in software-defined radio platforms for fast prototyping, WLAN indoor localization systems, and interference mitigation techniques for GNSS. He is a graduate student member of IEEE and ION.
Nikolaos Gatsis received a Diploma degree (Hons.) in electrical and computer engineering from the University of Patras, Patras, Greece, in 2005 and a M.Sc. degree in electrical engineering in 2010 and a Ph.D. in electrical engineering with a minor in mathematics in 2012 from the University of Minnesota. He is currently an Associate Professor with the Department of Electrical and Computer Engineering at the University of Texas at San Antonio. He was a Lutcher Brown Professorship Endowed Fellow for the academic year 2020–2021. His research focuses on optimal and secure operation of smart power grids and other critical infrastructures, including water distribution networks and the Global Positioning System. Dr. Gatsis is a recipient of the NSF CAREER award and the UTSA President’s Award for Research Achievement.
David Akopian is a Professor at the University of Texas at San Antonio (UTSA) and Associate Dean of Research for the College of Engineering. Before joining UTSA, he was a Senior Research Engineer and Specialist with Nokia Corporation from 1999 to 2003. From 1993 to 1999, he was a researcher, instructor and assistant director of a center at the Tampere University of Technology, Finland, where he received his Ph.D. degree in 1997. Dr. Akopian’s current research interests include algorithms for communication and navigation receivers, including fast acquisition and massive correlators, spoofing mitigation on different levels of processing chain, and the general area of mobile applications. Also, he contributed positioning algorithms for Assisted-GPS and Labview platform concepts for software-defined radio GPS receivers. Recent efforts include automated human-machine interfaces. He has authored and co-authored more than 35 patents and 170 publications. He has been a Fellow of the National Academy of Inventors since 2016. His research has been supported by the National Science Foundation, National Institutes of Health, USAF, the U.S. Navy, and Texas foundations.