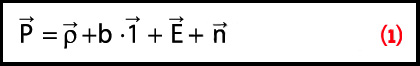Equation 1Q: How does measurement differencing affect my computed position?
A: The short answer is, “That depends.”
Standalone, or undifferenced, measurements obviously produce the poorest positioning performance. However, how we proceed from this most basic data processing approach may affect the computed solution. In this article, we look at the details of why this occurs.
Q: How does measurement differencing affect my computed position?
A: The short answer is, “That depends.”
Standalone, or undifferenced, measurements obviously produce the poorest positioning performance. However, how we proceed from this most basic data processing approach may affect the computed solution. In this article, we look at the details of why this occurs.
Measurements
We will initially concern ourselves only with pseudorange measurements, although the logic will apply equally to carrier phase and Doppler (phase rate) measurements. To this end, we will use the following simplified measurement model for the pseudorange
(see equation, above right)
. . .
Computing Position
For the purpose of our discussion, we will only consider least-squares as a means of estimating the unknown parameters . . . For the measurements in equation (1), the unknowns are the user position and the receiver clock bias.
Furthermore, because the measurements are non-linear functions of the unknowns, these are usually linearized to compute corrections to our current estimate of our unknown parameters . . .
. . .
Between-Receiver Differences
Differential GNSS (DGNSS) positioning is typically implemented by differencing measurements to common satellites observed at two receivers, one of which is typically occupying a known coordinate.
The unknown parameters in this case are essentially the same as before, except that we are now estimating the relative clock bias between the two receivers. (However, because the clock bias is not usually of interest, this factor is of no practical importance.)
. . .
Between-Satellite Differences
Unlike between-receiver differences, between-satellite differences only require one receiver. In this case, measurements to different satellites are differenced pairwise. Since any two observations from a given receiver made at the same time have the same clock error, this term is eliminated. Correspondingly, the vector of unknown parameters only contains the receiver position.
. . .
Double Differencing
As is well known, double differences are the combination of the two aforementioned single differences. More specifically, double differences can be considered as between-satellite single differences of between-receiver single differences.
. . .
A Look at Carrier Phase
Some might ask: given the last sentence, why is carrier-phase processing typically implemented using double difference processing? Why not use single-difference processing?
The main reason is the desire to estimate the carrier phase ambiguities as integers. In order to do this with between-receiver single differences, we need to separate the receiver clock bias from the ambiguity states. Although this is possible — see, for example, the November/December 2006 GNSS Solutions contribution on Precise Point Positioning by Dr. Yang Gao, which has a related problem — it can take a significant amount of time.
. . .
Summary
Between-receiver differencing reduces the errors that are present in the measurements, thus producing a more accurate position estimate. Between satellite differences do not change the position obtained (relative to the solution obtained using the observations being differenced), and are thus used only for practical reasons, such as simplifying the process of estimating the carrier phase ambiguities.
(For Mark Petovello’s complete answer to this question, including
formulas and tables, please download the full article using the pdf
link above.)
