Peer-to-Peer Cooperative Positioning

Working Papers explore the
technical and scientific themes that underpin GNSS programs and
applications. This regular column is coordinated by Prof. Dr.-Ing. Günter Hein, head of Europe’s Galileo Operations and Evolution.

As part of an effort to find methods that improve the performance of GNSS receivers in hostile environments, this article examines a cooperative positioning, where receivers exchange data and information with their neighbors or peers. We focus on unstructured peer-topeer (P2P) networks, without a control or data fusion center.

Our discussion will show that a significant reduction of the acquisition time can indeed be achieved when GNSS aiding quantities like Doppler, satellite carrier-to-noise ratio (C/N₀), and secondary code delay are provided by some aiding peers. The approach is clearly similar to that of assisted-GNSS (AGNSS), but does not require a fixed infrastructure and may better take into account the local environment.

As multi-standard devices will become more and more inter-connected in the near future, GNSS cooperative positioning may soon become an alternative or a complement to fixed augmentation systems.

The Cooperative Positioning Paradigm
Satellite navigation systems are typically characterized by a one-directional flow of information from the satellites to the users. Each receiver must be able to collect reliable data from a sufficient number of satellites to compute its position. When available, augmentation may be used to improve the receiver performance. Various systems (both satellite-based and ground-based) have been developed, but each user’s equipment must still process the received data individually. This situation is depicted in Figure 1.

The performance of a GNSS receiver is widely known to be very good in opensky conditions (at least four satellites in full view) but may strongly decrease in difficult situations, such as natural/ urban canyons, wooded areas, inside buildings, at high latitudes, or in the presence of electromagnetic interference. Such environments can adversely affect availability, time to first fix (TTFF), accuracy, and integrity.

Assuming a GNSS-hostile environment, in this article we want to give some answers to the question: Is it possible to improve GNSS receiver performance by allowing information exchange among users?

The basic idea that we examine here is how users in difficult conditions may receive and exploit aiding data from other nearby GNSS users, applying special techniques for computing their positions faster and with higher reliability. We then introduce the cooperative positioning (CP) paradigm, where data and information are shared within clusters of GNSS receivers to improve individual receiver performance.

Architecture: Centralized versus Peer-to-Peer
We can distinguish between types of CP methods based on the cluster architecture. As shown in Figure 2, the receivers’ network may be centralized (with a control center collecting all the data sent from the receivers, processing and enhancing the data, and sending aiding information back to the receivers), or decentralized (all the receivers behaving as peers and working without a central control unit).

In this column, we focus on the latter approach in which each receiver can share data with its neighbors in an unstructured way.

Figure 3 depicts the logical scheme of this approach, called peer-to-peer cooperative positioning (P2P-CP). Even though the presence of a control center could obviously simplify data exchange and elaboration, the P2P approach has the great advantage of not requiring a fixed infrastructure, allows scalability, and fosters the creation of heterogeneous time-varying networks with different receivers. (In any case, a centralized network could also adopt many of the techniques presented in this article.)

Exchanged Data: GNSS-Only versus Hybrid
A second distinction, following categories described in the Final Report on P2P by Politecnico di Torino listed in the Additional Resources section near the end of this article, can be made based on the differing natures of the exchanged data:

Cooperation based on the exchange of GNSS-only data. This approach requires that each user possess a GNSS receiver and a communication system for sending/receiving data. By GNSS-only data we mean data generated in GNSS systems or obtained by processing GNSS signals. Examples include information about visible satellites, their carrier-to-noise density ratio, Doppler, receiver observables, messages provided by the GNSS and augmentation systems, raw data, pseudoranges, computed altitude, computed position, and so on. GNSS-only is indeed the focus of this paper.
Cooperation based on the exchange of GNSS data and ranging data from non-GNSS-systems. This hybrid approach, called hybrid peer-to-peer cooperative positioning, requires that each user possess a GNSS receiver, a communication system, and a ranging system to estimate the distance from its neighbors. Ranges from the other peers can be used to integrate satellite pseudoranges and dramatically improve availability and accuracy of positioning in deep-indoor environments. Hybrid CP will be covered by a future companion paper in Inside GNSS.

Cooperative Positioning versus Assisted GNSS
P2P-CP can be particularly helpful for improving the performance of low-cost, mass-market receivers typically used by consumers by exploiting GNSS aiding data provided by neighboring users.

The improvements may take various forms, such as:

availability — aiding allows a receiver to estimate its position where it is usually impossible
accuracy — aiding reduces the position error
time to first fix — aiding reduces the time taken by the receiver to compute its first position estimation.

We can immediately see that most of these goals are the same as those of AGNSS (discussed in the book by F. van Diggelen listed in the Additional Resources section), although the latter method uses a fixed terrestrial infrastructure (typically, cellular network base-stations) to transmit GNSS aiding data to registered users.

AGNSS aiding may include, for example, GPS almanac (details on GPS constellation), GPS navigation model (mainly ephemeris to speed-up satellite position computation), integrity assistance (integrity information of the SIS of different satellites), satellite clock corrections, GPS acquisition assistance (ID of visible satellites, Doppler and code phase information), GPS ionosphere model (information on ionosphere delay), augmentation system assistance (differential corrections), reference time (to time-stamp the assistance messages), and reference position (a rough estimation estimation of the receiver estimation computed by the cellular network with a cell-ID approach).

Clearly, then AGNSS has many characteristics in common with P2P-CP and can be considered as a useful benchmark for addressing its performance. However, a comparison with AGNSS raises some important issues:

P2P-CP does not require an infrastructure. The AGNSS distribution network is not available everywhere and may in fact become unavailable (e.g., during an emergency situation). Moreover, the infrastructure expense and ownership may well mean that the AGNSS service is not free.
P2P-CP better takes into account the local environment. Even if AGNSS base-stations are not far from the receiver, they may observe satellites under different conditions. For example, some satellites may be received with a low signal-to-noise ratio (SNR) or be blocked by local obstacles.
P2P-CP aiding data could be exchanged as a (small) subset of a larger set of information shared by two peers. We can easily surmise that, in the not too far future, both portable devices and cars will exchange a lot of data with their neighbors in an opportunistic way. (We will discuss this issue further in a later section.)

All these considerations suggest that P2P-CP may be viewed both as a possible integration with and an alternative to AGNSS aiding. With this in mind, we can analyze which aiding data are better suited for a P2P-CP scenario.

Physical versus Range Layers
Referring to the scheme shown in Figure 4, within a GNSS digital receiver we can distinguish the physical layer and the range layer operating blocks. The first layer must compute the pseudorange measurements, while the second must output the user position.

With reference to these, the aiding quantities can also be divided into two classes:

aiding quantities that can be used at the physical layer, essentially for improving the acquisition techniques, and
aiding quantities that can be used at the range layer, for integration and/ or complexity reduction of the position/ velocity/time computation.

In the following section, we focus on techniques exploiting GNSS aiding at the physical layer in order to improve the acquisition process. (Examples of range-layer aiding techniques may be found in the Politecnico di Torino report.)

CP Methods at the Physical Layer
Consider a set of aiding peers that have already estimated their positions. To do this, they have evaluated a number of parameters. Certainly they have identified the visible satellites, computed their position and their Doppler, decoded their navigation messages, and so on.

Some of this information can be shared with a peer using a mass-market receiver that is just starting the acquisition phase in order to reduce the latter receiver’s acquisition time.

We assume that all the peers are equipped with both a GNSS receiver and a communication link that can send and receive data. The aided peer broadcasts a request for help and the aiding peer values. In this article we will focus on the following types of aiding data:

Doppler frequency shift, f_d(m), estimated by the mth aiding peer
carrier-to-noise ratio estimated by the mth aiding peer, C/N₀(m)
code delay, estimated by the mth aiding peer, t_S(m).

The definition of this code delay depends on the GNSS signal we are acquiring. In the case of the Galileo E1 band, the pilot signal can be used in the acquisition phase, and the code delay can be defined as the time difference between the initial instant for the first chip of the next secondary code period and the current time estimated by the mth peer, assuming a common time scale among all the peers in the cluster (synchronized clocks).

Weighting Coefficients
Because the information coming from different neighbor peers may have different levels of reliability, it is useful to introduce weighting coefficients to merge information provided by the aiding peers.

Let us denote by g(m) one of the aiding quantities received from the mth aiding peer (it could be f_d, C/N₀ or t_S). The aided peer receives the messages from N aiding peers and must combine them in some way to exploit them during its acquisition phase.

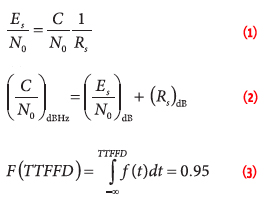
We assume that the aided peer performs a weighted sum of the data coming from the N aiding peers, thus:

Equation 1

where the set of values α_g(m) are proper weights for the quantity g(m).

The selection of these weights can be important. Some possible strategies are collected in Table 1, which we will now discuss.

Uniform weights. The simplest approach is to perform the arithmetic average of the aiding quantities received from the aiding peers, by using constant weights (see Table 1, row 1). This approach is reasonable if all the aiding peers have similar characteristics, or when no information is available on them.

Weights related to the aiding quality. Let us suppose that a reliability index, α_g(m), can be computed for the aiding quantity g provided by the mth peer. For example, this could be the standard deviation of the estimated g(m). This number could be evaluated and sent by the same aiding peer, or directly evaluated by the aided peer by comparing a set of received aiding values.

Given the values, we can use weighting coefficients inversely proportional to them, as shown in Table 1, row 2. The coefficient x is used to obtain a unitary sum of all the weights:

Equation 2

As an alternative, a simplified approach would be to use some fixed weights for α_g(m), depending on the quality of the corresponding aiding peer (e.g., mass-market receivers, low values; professional receivers, medium values; anchor peers, i.e., fixed GNSS receivers which know their position with very high precision).

Weights related to the distance. If the distance, d(m), between the aided peer and each mth aiding peer is known, we can define the weights as inversely proportional to the distance. (See Table 1, row 3.) Also, in this case the coefficient x is used to obtain a unitary sum of all the weights:

Equation 3

Closest peer approach. A simpler method for exploiting the knowledge of the distance between the peers is to select the closest peer and use only the aiding values provided by it, discarding all the other information. (See Table 1, row 4).

The first two weighting strategies can be easily implemented without a knowledge of the network topology. The last two, instead, require a rough knowledge of the topology of the cluster of peers, or at least an estimate of peers’ distance with respect to each other. (Other weighting strategies can be found in the Politecnico di Torino report cited previously.)

How to Exploit Doppler Aiding
An important aiding quantity that the neighbor peers can provide is the estimated Doppler frequency shift for each satellite in view. In fact, a rough knowledge of the Doppler frequency may allow a reduction of the size of the search space for the aided peer.

In this way, the acquisition system can compute the cross ambiguity function (CAF) in a reduced number of frequency bins close to the expected value and thus speed up the required acquisition time. A key role is played in this by the frequency synchronization between the set of peers.

Peer clock synchronization. Due to typical inaccuracies of local oscillators in mass-market receivers, Doppler aiding requires a certain level of synchronization between peers. In fact, if the peers have clocks that are sufficiently synchronized, they can distinguish between the Doppler shift due to satellite and receiver mobility and the deviation of their internal local oscillators.

A number of algorithms have been developed for clock sync in a peer-to-peer network mostly in the field of wireless sensor networks and femtocell systems. Some analyses (to be discussed in a later section) show that peer synchronization is important, but conventional approaches with limited complexity well explored in the literature appear sufficient to guarantee the requested accuracy.

How to Exploit C/N₀ Aiding
Additional useful information that the aiding peers may provide is the estimated C/N₀ for each satellite in view. By using these values, the aided peer can decide to start acquiring the satellites with a higher expected C/N₀. If all the satellites are expected to have a low C/N₀, the aided GNSS receiver can increase the integration time, choosing an adequate number of coherent and non-coherent integrations in order to improve the probability of detection.

In this case, some care must be taken to properly choose the weighting parameters. In fact, by performing some experimental trials, we observed that the C/N₀ values estimated under the same conditions by two commercial GPS receivers may differ by some decibels, i.e., the measurement variance may be large. If all the peers in the cluster are in an open-sky scenario, they are likely to estimate similar (high) C/N₀ values. A simple arithmetic average of their values can then produce a reliable estimation, reducing the variance. In this case, the number of aiding peers should be as large as possible.

The situation is more complicated in indoor environments. If the aided peer is deep inside a building, there is no way to compute the position using GNSS alone. Only hybrid positioning using terrestrial ranging can help it (as will be shown in the companion article on Hybrid CP to appear in a later issue).

If the aided peer is in a “light” indoor environment (e.g., in an urban canyon, or under foliage, or inside a room but near to a window), only the closest peers are likely to be in a similar situation (e.g., experiencing attenuation or signal blockage of part of the sky). In that case, only the C/N₀ values estimated by the neighboring peers should be taken into account. A limiting case could be to consider Approach 4 of Table 1 and use only the C/N₀ estimated by the closest peer.

Especially in indoor situations, the aiding provided by the C/N₀ is clearly more fragile when compared to the other ones (i.e., Doppler aiding and secondary code wipe off) that can still work without it. So, more research and development is needed to completely exploit this technique.

In any case, the alternative is to start with no information at all about the visible satellites. Then, at worst, C/N₀ may not improve the acquisition performance, but in many situations it could be very useful.

One note of interest: P2P differs from AGNSS regarding the availability of C/N₀ estimates. In fact, in 3GPP technical specifications for mobile communications (see Additional Resources), C/N₀ measurements are transmitted from the receiver to the base-station only in the case of network-based positioning where a mobile user’s position is computed in the base station and then sent back to the user. These measurements are not, however, included in the information provided by the base-station to the receiver for AGNSS positioning.

How to Exploit Secondary Code Delay Aiding
We have studied this method by taking as reference the Galileo E1c pilot channel. The Galileo E1 Open Service (OS) signal includes a data channel (E1b), featuring a pseudorandom code modulated by navigation data, and a pilot channel (E1c), that is a data-less signal useful for acquisition and tracking purposes.

Both channels include pseudorandom codes with a chip rate of 1.023 Mcps and are modulated using the composite binary offset carrier (CBOC) modulation scheme. The Galileo E1c channel features a tiered code structure, including a 4-millisecond primary code (with a length of 4,092 chips) overlaid by a 100-millisecond secondary code (25 chips) (For additional technical specifications, see the “European GNSS (Galileo) Open Service Signal In Space Interface Control Document” cited in Additional Resources).

The primary E1 OS code allows for fast acquisition approaches, exploiting its four-millisecond periodicity. However, the presence of the secondary code can lead to transitions at the end of each primary code period (an effect similar to that of navigation data transitions), impairing the correct code acquisition if not properly managed.

If an estimate of the secondary code delay is available to the aided peer with enough accuracy, it is possible to multiply the received signal samples by a local replica of the secondary code samples, in order to remove the secondary code transitions. Peer synchronization is again important, but in this case our analysis has again confirmed the feasibility of this aiding strategy in mass-market receivers.

Regarding the differences between P2P and AGNSS, we should point out that the secondary code delay aiding, focusing on the Galileo E1c secondary code, is not (yet) contained in the AGNSS standard. The base station can provide code phase and Doppler information for the visible satellites of the constellation. The code phase is provided to the receiver in terms of an integer number of milliseconds (integer code phase, expressed modulo 128 milliseconds) and fractions of a millisecond (code phase, ranging from 0 to 1 millisecond) with respect to a reference time.

Assistance data for Galileo signals in current 3GPP technical specifications are generally referred to as Galileo E1, E5a, E5b, E6, or E5a+E5b signals, without an explicit distinction between data and pilot channels. The secondary code delay for the Galileo E1c pilot channel is not explicitly mentioned in assistance information. Clearly, the peer synchronization plays a key role for both cooperative positioning and AGNSS.

Performance Improvements
As an example, the following discussion will present the results of a comparison among unaided techniques, AGNSS, and P2P-aided approaches. Mean acquisition time (MAT) simulations were carried out by post-processing real data collected from an experimental setup.

The considered approaches have been compared in two different scenarios (light indoor and open-sky conditions) and assume pedestrian or vehicular mobility of the peers. Errors due to the communication channel have not been introduced.

Receivers setup. The following assumptions were made in order to simulate an AGNSS-aided acquisition phase:

An assisted acquisition engine with an M of N detector is used, exploiting a serial search acquisition approach (capable of searching a few code delay bins and Doppler frequency bins around the assistance values) or a fast Fourier transform– based (FFT-based) parallel acquisition approach, depending on the availability of the code delay assistance. The serial search approach (searching for a few code delay bins) enables us to reduce the computational burden in the CAF computation but is applicable only with code delay assistance. On the other hand, it is reasonable to perform a full code delay search using the FFT-based approach when the code assistance is not available.
The initial coherent integration time, T_int, is fixed to eight milliseconds (one GIOVE-A primary code period) and is doubled (halving the Doppler search step at each repetition) until the CAF peak has been correctly detected.
C/N₀ aiding is not considered.
Code delay assistance is considered, assuming the case of AGNSS fine time synchronization (maximum synch error = 1 microsecond, corresponding to a code delay search range of two microseconds).
Doppler frequency assistance is used, taking into account typical sources of errors for the AGNSS approach in order to select a proper frequency search range in pedestrian and vehicular cases. In contrast, the P2P-aided acquisition phase is simulated using the following assumptions:
The three P2P aiding data (Doppler frequency, C/N₀, and secondary code delay aiding) are considered together.
The acquisition engine used in the AGNSS case is modified in order to fully exploit the P2P aiding information. In detail, an FFT-based parallel acquisition approach or a serial search acquisition approach is used, depending on the availability of the secondary code delay assistance. In the second case, a flexible serial search engine, capable of using an arbitrary coherent integration time (T_int, supporting also partial correlations of less than one secondary or primary code period), is adopted.
The initial coherent integration time, T_int, is fixed depending on the C/N₀ aiding, assuming a minimum initial T_int = 1 ms (lower than the primary code period of eight milliseconds). This approach exploits the C/N₀ aiding information in order to reduce the computational burden and then the MAT. If necessary, the initial T_int is doubled until the CAF peak has been correctly detected.
The Doppler frequency ranges are fixed depending on the user mobility (pedestrian and vehicular cases) and considering different possible synchronization techniques suitable for the P2P approach: (a) Tiny sync, which is a synchronization algorithm used in WSN, (b) a femtocell sync algorithm, and (c) an ad hoc developed software proprietary software.
A common code delay search range of two microseconds (close to the theoretical time synchronization provided by each approach) is considered for all three considered synchronization techniques.

We should note that these assumptions, especially the use of the same code delay search range (same accuracy for time synchronization), were made in order to have a fair comparison between the various approaches under consideration. In fact, such synchronization accuracy represents a favorable condition for the AGNSS case because asynchronous networks (like GSM and UMTS networks available in Europe) can only provide coarse-time assistance with a time synchronization accuracy no better than 2–3 seconds. Fine-time assistance (with an accuracy of 1-10 microseconds) can only be provided by synchronous networks (e.g., available in the United States).

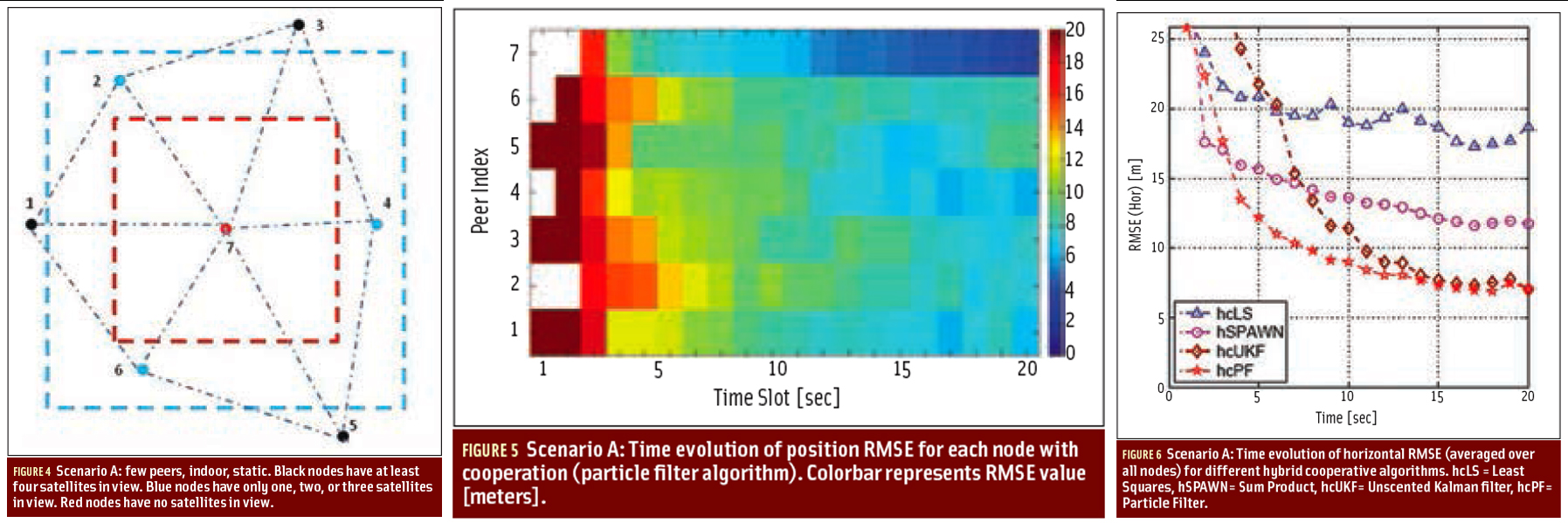
Results. Figure 5, summarizes the obtained results in terms of MAT. These results compare the performance of unaided approaches, AGNSS-like approaches, and P2P approaches.

As can be observed, use of AGNSS clearly reduces the MAT with respect to the unaided approach (four to five times lower in open-sky conditions, and five to seven times lower in light indoor conditions). P2P techniques show further advantages in terms of MAT: almost half of the values corresponding to the AGNSS case in light indoor conditions, and a net advantage of almost 40 times faster MAT with respect to AGNSS in open-sky conditions.

Effects of aiding quantities. Different aiding quantities make different contributions to the overall acquisition performance, depending on how the aided acquisition algorithm is implemented and on the accuracy of the available aiding information (connected to the size of the search space).

The obtained results can be summarized as follows:

Availability of an estimate of the Doppler frequency shift of the signal allows us to strongly reduce the size of the search space and then to speed up the MAT in all configurations.
Absence or availability of the code delay information reasonably determines the choice of the FFT-based or the serial search approach. Better performance is typically obtained with the latter method, if the available aiding information enables us to sufficiently reduce the code delay search range.
P2P C/N₀ aiding (which is an innovation with respect the AGNSS setup) is able to potentially provide the largest benefits in terms of MAT reduction, but only if the secondary code delay aiding is also available.

In fact, combining the last two bulleted items allows exploitation of a serial acquisition engine supporting partial correlations, where the coherent integration time (T_int) is fixed depending on the expected C/N₀. This leads to a large reduction of the computational burden, decreasing T_intup to one millisecond in open-sky conditions.

On the other hand, if the C/N₀ aiding is used without secondary code aiding, the results in terms of MAT are similar to the case without C/N₀ aiding. These results are motivated by the fact that, without secondary code aiding, a full primary code search must be performed using the FFT-based approach, in which case T_int is then fixed to be at least eight milliseconds. This assumption proves to be a bottleneck, because T_int is fixed to a minimum value that is larger than the optimal values that can be computed exploiting the C/N₀ aiding.

Aiding accuracy. We must point out that possible errors on the aiding quantities exchanged between the peers can impair the acquisition performance, thus degrading the receiver sensitivity, robustness, and/or the MAT. For example, time and frequency synchronization errors can reduce the benefits of secondary code delay and Doppler frequency aiding, whereas inaccuracies in C/N₀ estimated values can lead to an incorrect setup T_int, slowing down the acquisition time.

In fact, multiple repetitions, doubling T_int, may be needed in case of an initial T_int too low with respect to the optimal value. On the other hand an excessive T_int results in a waste of computational resources, because the number of Doppler bins to be explored increases with T_int. (More details can be found in the Politecnico di Torino report.)

We can thus conclude that GNSS cooperative positioning is very promising and allows an aided peer to achieve performances, which are (1) certainly better than those of unaided acquisition, and (2) similar to those obtained with AGNSS aiding, but without requiring a fixed infrastructure. (Currently, two patents by R. Garello et alia, and M. Rao et alia are pending on P2P GNSS cooperative positioning. Other information on the developed techniques can be found in Additional Resources.)

Value Added by Professional Receivers
Given a cooperative network of GNSS receivers, an interesting issue is the positive impact of professional receivers on the network performance. Professional receivers are high-end, multiband devices with higher computational power. They are able to provide aiding quantities with very good accuracy.

Moreover, some algorithms that are too complex for consumer receivers could be implemented on professional units. Within the cluster of peers with mixed types of receivers, “difficult” operations could be handed off to professional receivers that can then broadcast their results to the entire network, including mass-market user equipment.

Consider the challenge of interference mitigation. Interference detection and identification is known to be a computationally expensive task. As an example, detection may be based on different techniques (signal energy, cyclo-stationary properties, high order statistics, direction of arrival), but these typically require a computational power not available for mass-market receivers.

However, complex operations could be delegated to peers with professional quality equipment to perform, including such tasks as interference detection, estimation of interference parameters, and creation of an interference electromagnetic map.

This information could then be shared within the network and massmarket users could apply low complexity mitigation techniques (e.g., single sideband processing, interference excision, pulse blanking). This approach could make increased robustness against interference available for all network peers.

Conclusions and Issues for Real-Time Implementation
A number of issues concerning the practical realization of P2P cooperative positioning must be considered, such as computational complexity, latency, scalability with an increasing number of peers, energy consumption, synchronization, communication protocols, aiding data format, user incentives to encourage cooperation, and security aspects. A number of these items have been discussed in the Politecnico di Torino report among others.

As a matter of fact, thanks to their limited complexity, all the presented techniques are already implementable on ad hoc devices that contain both a GNSS receiver and a communication system. Thus, GNSS cooperative positioning could already be adopted for some applications — wireless sensor networks, an “Internet of things,” and so forth — on properly programmed proprietary nodes.

Moreover, we can anticipate that this approach will soon become realizable for commercial low-end devices. It is true that mass-market GNSS receivers may not possess a communication system for sending/receiving data and have a small computational power. However, we can reasonably assume that these features will be available for such devices in the near future, as the next generation of multi-standard portable devices will be able to cover a number of GNSS and terrestrial wireless systems (with some of them suitable for ranging, too).

Furthermore, these future devices will be more and more interconnected. As an example, car devices are going to share mobility information. Car manufacturers are putting significant R&D into this topic. New protocols for Vehicular Ad-Hoc Networking (such as WAVE, a modified version of WiFi — see IEEE citation in Additional Resources) and for short-range communications have been developed and will soon be operative.

Within this flux of information, GNSS aiding data could also be shared. Portable devices will similarly move in this direction and users will exchange messages with their neighbors. Because GNSS cooperative positioning has performance similar to that of AGNSS but requires no infrastructure, we believe it could become an interesting alternative (or complement) to fixed augmentation systems.

Additional Resources
[1] Deambrogio, L., and C. Palestini, F. Bastia, G. Gabelli, G. E. Corazza, and J. Samson, “Impact of High-End Receivers in a Peer-To-Peer Cooperative Localization System,” The International Conference on Ubiquitous Positioning, Indoor Navigation and Location-Based Service, UPINLBS 2010, Helsinki (Kirkkonummi), Finland, 14-15 October 2010
[2] ETSI, “Dedicated Short-Range Communications (DSRC).”
[3] ETSI 3GPP, “Universal Mobile Telecommunications System ( UMTS); Radio Resource Control (RRC); Protocol specification,” 3GPP TS 25.331, Version 9.1.0, Release 9, February 2010
[4] ETSI 3GPP, “Digital Cellular Telecommunications System (Phase 2+); Location Services (LCS); Mobile Station (MS) – Serving Mobile Location Centre (SMLC) Radio Resource LCS Protocol (RRLP),” 3GPP TS 44.031, Version 9.2.0, Release 9, March 2010
[5] European Union, “European GNSS (Galileo) Open Service Signal In Space Interface Control Document,” OS SIS ICD, Issue 1, 2010
[6] Garello, R., and L. Lo Presti, F. Dovis, D. Margaria, and J. Samson, “Sistema di posizionamento geo-spaziale cooperativo operante con sistemi di navigazione globale satellitare e reti di telecomunicazione wireless, relativo procedimento e apparato di posizionamento geo-spaziale: P2P aiding,” Patent Application No. TO2010A000718, 30/09/2010
[7] IEEE, “IEEE 1609 Family of Standards for Wireless Access in Vehicular Environments – WAVE.”
[8] Lo Presti, and L., D. Margaria, and J. Samson, “A Novel Peer to Peer Aided Acquisition Strategy Tailored to Galileo E1 Receivers,” 52nd International Symposium ELMAR-2010, Zadar, Croatia, 15-17 September 2010
[9] Margaria, D., and L. Lo Presti, N. Kassabian, and J. Samson, “A New Peer-to-Peer Aided Acquisition Approach Exploiting C/N₀ Aiding,” 5th ESA Workshop on Satellite Navigation Technologies, NAVITEC’ 2010, Noordwijk, The Netherlands, 8-10 December 2010
[10] Politecnico di Torino, Università di Bologna, Istituto Superiore Mario Boella, “Peer-to-Peer Positioning – Final Report,” ESA Contract No. 22868/09/NL/A, April 2011
[11] Rao, M., and L. Lo Presti, and J. Samson, “Peer to Peer Equation Augmentation for an Altitude Aided GNSS Receiver,” 2010 IEEE 72nd Vehicular Technology Conference, VTC 2010-Fall (Track: Mobile Satellite and Positioning Systems), Ottawa, Canada, 6-9 September 2010
[12] Rao, M., and L. Lo Presti, and J. Samson, “Improved GNSS positioning exploiting a vehicular P2P infrastructure,” 5th Advanced Satellite Multimedia Systems Conference, ASMS2010, Cagliari, Italy, 13-15 September 2010
[13] Rao, M., and L. Lo Presti, and J. Samson, “Sistema di posizionamento geo-spaziale cooperativo operante con sistemi di navigazione globale satellitare e reti di telecomunicazione wireless, relativo procedimento e apparato di posizionamento geo-spaziale,” Patent Application No. TO2010A000719, 30/09/2010
[14] Rao, M., and L. Lo Presti, and J. Samson, “Iterative Altitude-Aiding Algorithm for Improved GNSS Positioning,” IET Radar, Sonar & Navigation, 2011
[15] van Diggelen, F., A-GPS: Assisted GPS, GNSS, and SBAS, Artech House, 2009

Download this article (PDF)

Related Posts: