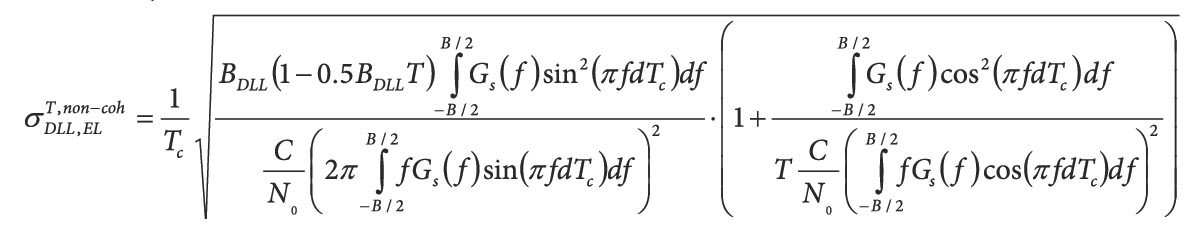EquationsWorking Papers explore the technical and scientific themes that underpin GNSS programs and applications. This regular column is coordinated by Prof. Dr.-Ing. Günter Hein, head of Europe’s Galileo Operations and Evolution.
Working Papers explore the technical and scientific themes that underpin GNSS programs and applications. This regular column is coordinated by Prof. Dr.-Ing. Günter Hein, head of Europe’s Galileo Operations and Evolution.
Since March 2011 the European Geostationary Overlay System (EGNOS) has provided integrity information throughout Europe. This allows aircraft to perform approaches to an increasing number of European runways without the need of expensive ground-based navigation equipment.
With the Global Positioning System being upgraded, the Russian GLONASS constellation having reached full operational status again, and all four Galileo in-orbit-validation (IOV) satellites being in orbit, the number of dual-frequency pseudorange sources is quickly increasing. China is also deploying its own GNSS, BeiDou. The resulting large number of usable GNSS signals not only has an effect on the availability of the GNSS services (e.g., in urban environments) but may also allow new integrity concepts based on multiple constellations.
Navigation in Commercial Aviation Today
For many decades the primary means of navigation has been based either on ground-based systems (radio navigation) or inertial systems (gyroscopes). The accuracy and durability of these systems has improved over the years so that precision approach operations are common nowadays.
In commercial aviation, navigation is usually performed using radio navigation aids. For final approach and landing, either visual cues or RF-based guidance systems can be used. All these systems, however, require maintenance and frequent calibration in order to ensure continuous availability. Moreover, the existing systems’ versatility is limited.
With GNSS-based air navigation, many of these disadvantages can be overcome. Aircraft now could perform curved approaches to improve airspace capacity or to implement steep approaches for optimal noise abatement (see T. Lüken et alia in the Additional Resources section). Further, because fewer navigation beacons are needed, the costs of ground-based systems can be reduced significantly, making them attractive for smaller airports as well.
In order to use GNSS as the primary source for navigation in aviation, stringent requirements have to be met. GNSS use in safety-critical applications makes integrity mandatory: the timely provision of information to users about the level of trustworthiness of a position solution by defining the maximum deviation from the true position with a certain amount of probability.
GNSS Integrity Systems
Several methods exist to provide integrity. One well-established method of distributing integrity information uses of space-based augmentation systems (SBASs). These employ a combination of monitoring stations distributed across the area of interest and a master control station that processes the positioning inaccuracies for generating the integrity message. Finally, a set of uplink stations transmits the correction information via geostationary satellites for re-transmission to users.
Because the true positions of the monitoring stations are known and can be compared with the computed position solutions at these locations based on GNSS signals in space, the integrity and accuracy of the signal can be determined and forwarded to users.
Another approach is the ground-based augmentation system (GBAS). Here, ground monitoring stations located close to airports are used, which transmit correction signals directly to the aircraft via RF links. Integrity information can be obtained by comparing the true position of the ground station with the calculated position solution from the GNSS constellation.
Both SBAS and GBAS are very powerful methods to provide the user with integrity information. However, their infrastructure is very complex and therefore costly. The requirement for informing the user about a loss of integrity within seconds demands a high amount of computing power and facilities.
A third way of providing integrity information is to perform calculations within the user equipment itself, which is called receiver autonomous integrity monitoring (RAIM). Most of the time sufficient satellites are visible to support multiple redundant position calculations — the crucial element of RAIM techniques — from which a level of integrity can be derived.
Based on GPS, several SBASs have been implemented. The U.S. Wide Area Augmentation System (WAAS) covers the continental (or contiguous) United States (CONUS) and most parts of Alaska, Canada, and Mexico. The European GNSS Navigation Overlay System (EGNOS) provides integrity and improved accuracy for the European continent.
Also, Japan and India have implemented their own SBASs, called Multi-functional Satellite Augmentation System (MSAS) and GPS Aided Geo Augmented Navigation (GAGAN), respectively. Russia is implementing a WAAS-compatible SBAS covering their territory (System for Differential Corrections and Monitoring, or SDCM).
Aviation Requirements
Although all three existing methodologies (SBAS, GBAS, and RAIM) provide integrity information, they do not achieve the same level of integrity. Depending on an aircraft’s approach mode, it must operate with a more or less stringent alert limit.
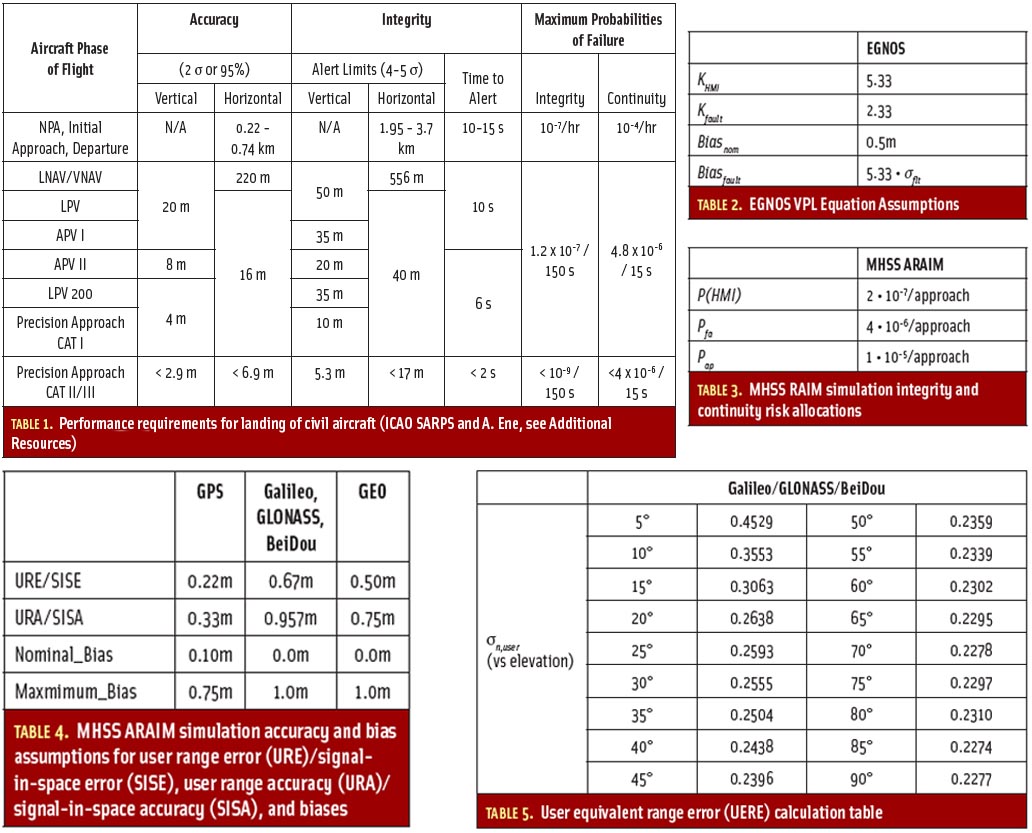
The alert limit is defined as the error tolerance not to be exceeded without issuing an alert. The protection level defines the estimated error bound provided by the integrity system. Because the protection level must always be smaller than the alert limit, the requirements for the integrity system increase with decreasing alert limit. Table 1 lists the most common approach modes and the associated alert limits according to the International Civil Aviation Organization (ICAO) standards and recommended practices (SARPS).
SBAS systems are aiming at providing integrity down to the LPV-200 level. LPV-200 is a newly introduced approach mode that provides lateral performance with vertical guidance down to a decision height of 200 feet.
As of today, GBAS is the only GNSS-based system that can provide the integrity performance necessary for precision approaches (up to CAT-III). However, civilian airports have rarely implemented GBAS, which does not provide the advantages of a reduced ground segment that SBAS does.
With more independent GNSS constellations being deployed, an increased number of navigation sources will be available in the future. This will influence the performance of dual-frequency EGNOS and other SBASs (if upgraded to dual-frequency operation like EGNOS) as well as improved RAIM algorithms, which this article further investigates.
SBAS and Possible Future Improvements
As of today all SBAS systems only augment the civil L1 signal of GPS. The protection level is specified by the RTCA standard RTCA/DO-208, “Minimum Operational Performance Standards for Airborne Supplemental Navigation Equipment Using Global Positioning System” as:
Equation 1 (for all equations, see inset, above right)
where G is the geometry matrix and W is the weighting matrix with the diagonal elements being the inverted pseudorange variances with:
Equation 2
By only transmitting the total variance, σi, a user is able to determine the vertical protection level (VPL) — but at a high cost: a σi must be selected that is large enough to sufficiently bound even rather theoretical conditions where large errors occur simultaneously to several satellite/receiver pseudoranges at the same time.
Receivers must account for ionospheric delays to signals propagating through the atmosphere, the largest error contributor in the user equivalent range error (UERE) budget for a single-frequency user, by incorporating into their position solutions the GIVE (grid ionospheric vertical error) information determined by the SBAS ground network. Local effects of the ionosphere need to be covered by a sufficient overbounding methodology, which is unavoidable from a safety perspective. However this may potentially lead to a very conservative VPL.
With the GPS Block IIF satellite upgrade to a dual-frequency civil signal (L1+L5) in progress, the pseudorange error will be significantly reduced as the dual-frequency linear combination of the range measurements cancels out the first-order ionospheric error directly at the user level. Additionally, as proposed in the article by T. Walter et alia (2010), improvements can be made to the VPL determination by considering a more realistic treatment of the variances and by adding bias terms to better map faults with non-Gaussian behavior.
This proposal distinguishes between two hypotheses: Fault-free (H0) and faulted (H1). In the fault-free condition, the VPL is determined as follows:
Equation 3
For faulted conditions, the VPL is calculated like this:
Equation 4
with s0(3,i) projecting the ranging error onto the vertical position estimate and σ2ff,i being the expected error variance under nominal (fault-free) conditions. For the H0 case, a bias term is added to account for nominal non-Gaussian errors. In H1 the maximum bias under faulty conditions is also added.
Finally, the user VPL is
Equation 5
Additionally, the transition from Message Type 27 to Message Type 28 (MT28) on WAAS/SBAS satellites will in general reduce the user differential range error (UDRE) — the confidence bound on GPS/GEO clock and ephemeris corrections — and thus improve availability and integrity, discussed further in T. Walter et alia (2001).
Figure 1 shows the improved availability of integrity of an upgraded EGNOS based on dual-frequency GPS and with MT28 implemented.
Evolution of RAIM Algorithms
RAIM algorithms have been investigated since the late 1980s starting with publications by Y. C. Lee (1986), R. G. Brown et alia, and M. Brenner (1990).
This section presents three different RAIM algorithms and explains their capabilities with respect to improved integrity. The first one is the Least-Squares-Residuals (LS) RAIM algorithm that is typically implemented in today’s aviation grade GPS receivers and provides low-precision lateral integrity only. The second RAIM approach is based on the Separation Solution (SS) method.
Lastly, we present the Multiple Hypothesis Solution Separation (MHSS) method, which is an improvement on SS RAIM. MHSS seems to be a promising algorithm to allow vertical guidance up to LPV-200 capability based on just two independent constellations. An optimization of the MHSS RAIM method is also presented which further improves the overall integrity performance especially in multiple satellite failure conditions.
LS RAIM. This algorithm compares the size of the least squares residuals of redundant pseudorange measurements. If one of the measurements is faulty, the residuals will become large. By defining a threshold for the residuals and a test statistic, a receiver can determine whether a position solution is valid or faulty.
In 1995, T. Walter and P. Enge (see Additional Resources) improved the LS method by including individual weighting of the pseudorange measurements, depending on the elevation angle. In order to identify a measurement fault, an error slope is computed for each satellite and then compared to the maximum allowed error slope (or error threshold). The vertical protection level can then be calculated by
Equation 6
where T is the detection threshold, which depends on the number of satellites N and the desired probability of false alarms PFA. The factor k(PMD) is the distance (in number of standard deviations) from the specified integrity risk (PMD). The vertical positioning confidence is given by σv.
RAIM in Aviation (TSO-RAIM). In aviation, RAIM is used to improve the integrity of GPS receivers during en route, terminal, and non-precision approach phases of the flight. However, as of today no RAIM implementation exists for any application requiring integrity in the vertical plane (i.e., precision approaches), which has more stringent certification requirements.
Errors in vertical navigation are considered to pose a higher safety risk and are therefore designated “Hazardous” in the International Civil Aviation Organization (ICAO) Safety Management Manual (Doc. 9859), compared to “Major” for horizontal errors. This leads to a much more stringent assessment of possible errors that must be considered if RAIM is extended to support vertical navigation.
In literature on the subject, RAIM algorithms that also provide protection against vertical errors are often called “Advanced RAIM” (ARAIM) algorithms. Moreover, note that input parameters for the ARAIM algorithm will most likely need to be provided by an ARAIM ground-monitoring network compliant with the necessary safety requirements.
For the certification of airborne GPS receivers limited to lateral navigation, the Federal Aviation Administration (FAA) published a Technical Standard Order (TSO-C129a), which is based on DO-208. It does not precisely specify which RAIM algorithm is to be used. Instead, a test scenario is defined and the required availability output is given: “The RAIM function shall provide worldwide availability of at least 95% […]”.
The LS RAIM algorithm meets the TSO requirements and is therefore sometimes called TSO-RAIM. We adopted LS RAIM as the baseline RAIM algorithm for the simulations performed in the context of this article.
Solution Separation RAIM. A very different RAIM method was proposed by Brown et alia, called Solution Separation (SS). Since the number of received signals usually come from more than the minimum four satellites, the position can be determined based on a subset of the available satellites only. If one faulty satellite is present, then one of the subsets will contain only healthy satellites. The early SS RAIM approaches for detecting faulty satellites were based on a comparison of the position estimates of all subsets in the position domain, as described in the article by M. Brenner (1995).
Compared to LS RAIM, the Solution Separation method is able to detect multiple satellite failures (however at high computational cost). For this purpose, the probability of a satellite failure (Psat) is computed to determine the probability of multiple simultaneous satellite failures. The VPL is determined for all subsets:
Equation 7
with xv being the vertical component of the navigation error (i.e., the difference between the estimated position with the partial and all-in-view satellite sets) and k(PMD) representing the distance (in number of standard deviations) from the specified integrity risk value. Again, σv is the vertical positioning confidence.
As with LS RAIM, SS RAIM also adds a confidence interval σv to the vertical error in order to protect the user against the very hypothetical combined error along all LOS. For SS RAIM this means that the maximum position solution separation between a subset and the all-in-view case is considered as the condition against which the algorithm must protect, even though the probability of failure that leads to that subset is extremely low. (See the article by A. Ene for further discussion of this point.)
Multiple Hypothesis Solution Separation RAIM. To avoid this overly conservative requirement in SS RAIM, another approach analyzes every threat with respect to its probability of occurrence. The Multiple Hypothesis Solution Separation RAIM algorithm (MHSS) “… weighs fault modes based on their (prior) probability and eliminates the comparison against a given error threshold.” This method was first presented in the 1987 article by B. Parkinson et alia cited in Additional Resources.
A common approach is to equally allocate the allowable integrity risk P(HMI) among all possible fault modes (equal allocation). This results in the “… maximum conditional probability of detection regardless of which satellite fails,” as stated in the article by Y. C. Lee (2007).
In order to meet the more stringent requirements necessary for LPV-200, the MHSS RAIM algorithm must take into account biases in range measurements and utilize user range error (URE) or user range accuracy (URA) for the evaluation of accuracy and integrity. The VPL equation for the nth subset is then
Equations 8 & 9
represents the detection threshold for the nth test statistic.
This threshold depends on the false alert probability factor Kffd,n and the standard deviation of the difference between the full set and the nth subset in the vertical plane σdV,n. A bias term is also added, which ensures that the false alert probability is still met even with biases present in the range measurements.
Furthermore, an integrity buffer is added:
Equation 10
with Kmd,n being the missed detection probability factor. Finally, the total VPL is determined by
Equation 11
The factors Kffd,n and Kmd,n must be selected so that the continuity and integrity requirements are met. An easy way to achieve this is to equally divide the total false alert probability requirement among all satellites in view (N):
Equation 12
Here, Pfa is the probability of false alarm. In the same way the total allowable integrity risk is divided among all satellites, taking into account the a priori probability Pap,n of each satellite:
Equation 13
where Q-1 stands for the inverse of the complement of the one-sided standard normal cumulative distribution function, CDF.
However, this results in varying Dn, which directly influences the VPL. In order to optimize the allocation of the integrity and continuity budget, a method must be found that results in identical VPLn for all n = 1,2 …, N (outlined in Phase II of the FAA’s GNSS Evolutionary Architecture Study).
MHSS RAIM Optimization. The article by Blanch et alia (2010) describes such a mathematical approach to optimize the integrity and continuity allocation at the same time. The algorithm works as follows.
Find x and μ such that:
Equations 14, 15, 16 & 17
One way to find x and μ is to select one of the two constraining equations (14) or (15) and determine x(μ). Then, by moving along that function we find the point where both (14) and (15) are fulfilled. This process must be performed numerically and requires a large amount of processing time. However, by selecting upper and lower bounds beforehand and by using interval halving, the computational burden can be lowered significantly.
Simulation Assumptions
All simulations presented here aim to represent the situation as it is assumed to be circa 2025. This includes the presence of up to four fully operational GNSS constellations (GPS, Galileo, GLONASS, and BeiDou), which provide dual-frequency navigation signals.
We modeled the constellations based on either real orbit parameters (GPS) or the expected constellation geometry (Galileo, GLONASS, and BeiDou). We assumed that the ground segment of EGNOS has been upgraded by additional reference stations in North Africa to a total of 41 stations (see also Figure 2). We also assumed that Message Type 28 is being transmitted.
EGNOS Simulation Assumptions. The assumptions for the dual-frequency, dual-constellation EGNOS scenarios are derived from the single frequency VPL assumptions from the RTCA document, “Minimum Operational Performance Standards for Global Positioning System/Wide Area Augmentation System Airborne Equipment (GPS/WAAS MOPS),” using improved equations — Equation (3) to (5) introduced earlier — to calculate the VPL. Additionally, we selected the parameters shown in Table 2.
The total fault-free error is modeled as follows:
Equations 18 & 19
and σair,j are σtropo,i determined as described in the GPS/WAAS MOPS for the Airborne Accuracy Designator B type of receivers.
ARAIM Simulation Assumptions. Here, the MHSS algorithm with optimal integrity and continuity allocation was used as described in the article by J. Blanch et alia (2010). Table 3 shows the assumptions for the ARAIM simulations.
These values are based on the ICAO SARPS requirements and were confirmed to be suitable for LPV-200 ARAIM simulations in J. Blanch et alia (2011).
In terms of accuracy and biases, Table 4 shows our assumptions.
A few notes regarding Table 4 are required. Compared to other publications on this topic, the accuracy assumptions for GPS made here could be considered optimistic. However, because this article investigates the performance of a multi-constellation system that would be in place 12 years from now, we incorporated the expected improvement of GPS by adding GPS Block III satellites to the constellation that will be made possible by the Block IIIs’ rather low URE and URA.
The minimum allowed elevation angles (masking) were selected to be 5 degrees for the GPS constellation and 10 degrees for all others.
All scenarios include two geostationary navigation sources representing a possible future upgrade of the EGNOS space segment to support Galileo-like range measurements from GEO. The accuracy assumptions for GEO were taken from EGNOS testing.
The elevation-dependent ranging budgets (including receiver noise, multipath effect, ionospheric delay, and tropospheric delay) are determined in two different ways. For the GPS constellation, we used the formulas from the GPS/WAAS MOPS for the Airborne Accuracy Designator A type, adapting them for dual-frequency operation:
Equation 20
For the Galileo, GLONASS, and BeiDou constellations, the UERE is based on a lookup table given in Table 5 with linear interpolation between the steps.
Scenario Setup
The simulations presented here were performed using ESA’s service volume simulator GAIA, which was developed within the GNSS Evolution Team and recently upgraded to support the MHSS RAIM. In order to facilitate comparison of the simulations with the results presented in other publications, the results are presented with charts using the same layout as the popular Matlab Algorithm Availability Simulation Tool (MAAST) from Stanford University.
The main goal of the simulations performed for this article is to compare the performance of modern ARAIM algorithms with an upgraded EGNOS and various numbers of available GNSS constellations, assuming that EGNOS will eventually be providing corrections and integrity data for all four GNSS constellations, not just GPS. For that reason, we conducted several simulation runs using the same algorithm (either EGNOS or ARAIM) but adding more and more constellations to the scenario.
The duration of both the EGNOS and ARAIM scenarios were set to 10 sidereal days, which is the orbital repeat period of Galileo. We selected a time step of 300 seconds with a user location spacing of 2.5 by 2.5 degrees.
The scenario set starts with a constellation of 18 GPS satellites and two GEO navigation sources, representing the (hypothetical) situation of an underperforming GPS constellation or the situation when fully operational capability (FOC) for GPS L5 has not yet been achieved. The GPS satellites’ and GEO navigation sources’ orbital parameters are based on a two-line element (TLE) file published on February 18, 2011, with the locations of the two geostationary navigation sources using the orbital parameters of the satellites Artemis and AOR-E.
For the simulation runs presented in this article, more and more GPS satellites are added to the scenario until a total number of 30 is reached, representing the situation as it is today. Next, Galileo satellites are successively added including the initial operational capability (IOC) constellation size (18 satellites) and finally the FOC geometry (27 active satellites).
In the following run, 24 GLONASS satellites are added to the scenario. Here, we assumed that the performance of an upgraded GLONASS constellation would be similar to the Galileo constellation in terms of URA and probability of failure.
Finally, 24 satellites are added representing a future BeiDou constellation, resulting in a total of 105 satellites. Again, a performance similar to the Galileo satellites is assumed for BeiDou. As of today the BeiDou constellation is expected to consist of 35 active satellites.
We used a pure Keplerian propagator to predict orbital parameters. The Earth was modeled using the WGS84 ellipsoid.
Simulation Results
The following section describes the results of this progressive series of simulated scenarios.
Multi-Constellation EGNOS. Figure 2 shows the 99.9 percentile of VPL using two dual-frequency constellations (GPS and Galileo) consisting of 28 (nominal GPS constellation assumption in 2010) and 27 Galileo satellites, respectively. As a result, the VPL throughout the Central European region is below 10 meters.
In order to analyze the performance of EGNOS with respect to an increasing number of monitored satellites, two user locations were selected and investigated in more detail: one in the Central European region (Lat/Lon 50°/0°) and one in the Southern African region (Lat/Lon 30°/0°). The best performance of EGNOS is expected in the Central European region, where the density of the ranging and integrity monitoring stations (RIMS) is the highest. The second location is relatively far away from the specified EGNOS coverage area; therefore, higher protection levels are generally expected here.
If we look at Figure 3, we see that the EGNOS performance improves as the number of monitored satellites increases. For the Central European region, however, the improvement is not particularly significant when compared to the Southern African region. If EGNOS could be based on three fully deployed dual-frequency constellations, VPLs needed to achieve LPV-200 would even be achieved in the Southern African region.
One should keep in mind, though, that further requirements exist for LPV-200 in addition to the VPL (e.g., the 4-meter 95 percent accuracy requirement, the 10-meter fault-free 10-7 vertical position error requirement, or the 15-meter effective monitor threshold requirement), as discussed in the paper by J. Blanch et alia (2011). The results presented here can therefore only indicate a tendency of the capabilities of an upgraded multi-constellation EGNOS.
ARAIM. In the same way as for EGNOS in Figure 2, Figure 4 displays the VPL based on two constellations (GPS and Galileo) using ARAIM, in this case, the MHSS algorithm. These two figures allow for easy comparison of the characteristics of EGNOS and ARAIM-based integrity.
In terms of performance improvement with increasing number of constellations, we can say that one fully operational constellation (consisting of 28 satellites) is already sufficient to reach acceptable protection levels (see Figure 3).
We must remember, however, that ARAIM based on a single constellation increases the effect of a common-mode failure, which immediately results in a loss of integrity. With more constellations available, integrity could still be provided in such situations.
The simulations show that the MHSS ARAIM concept can achieve VPL levels similar to EGNOS. With a fully deployed Galileo constellation, Vertical Protection Levels well below 35 meters are possible, supporting LPV-200. Adding a third constellation allows even VPL ranges for CAT-I precision approach conditions to be reached.
Figure 3 also shows that for ARAIM integrity, the user location does not really influence the achievable protection level. On the other hand, the performance of ARAIM is extremely dependent on the number of satellites available.
Open Points and Outlook
The results presented in this article show the possibilities of both ARAIM and an upgraded EGNOS in the context of an increasing number of GNSS constellations. However, many important issues still need to be investigated further when comparing ARAIM and EGNOS. We will discuss some of these here.
Failure Modes for ARAIM. A EU/US ARAIM Working Group identified several potential errors that pose a threat to the ARAIM integrity system, which are elaborated in the previously reference paper by J. Blanch et alia (2011). The threats have been classified as “nominal,” ”narrow failure,” and “wide failure” errors.
Nominal errors can occur when all parts of the system are in their nominal operational state. This includes errors that cannot be avoided during operations in this state (e.g., nominal clock and ephemeris errors, nominal signal deformation errors, antenna biases, tropospheric errors, or code noise and multipath errors). Ionospheric effects are not considered as part of nominal errors, because dual-frequency systems that allow the cancellation of the first-order ionospheric effects are assumed to be in use.
Narrow failure errors are errors of the ground segment or the space segment that only affect one satellite. The source can be clock and ephemeris estimation errors, signal deformations, or code-carrier incoherence.
Wide failure errors result in a degradation of the navigation signal and the navigation message of more than one satellite. These errors can originate from inadequate manned operations or failures in the message generation process. This type of error can also arise from a failure in the spacecraft control segment. Finally, erroneous Earth orientation parameters (EOP) could induce a constellation-wide error, rendering an entire constellation invalid. Therefore, constellations need to be monitored by independent observations to quickly detect possible EOP errors.
Several ways to mitigate expected threats have been considered. As suggested by J. Blanch et alia, either the ground segment or the ARAIM algorithm must cover such contingencies, depending on the type of threat and its associated threat dynamics either the ground segment or the ARAIM algorithm must cover it.
Guarantors for the ARAIM. Various methods to guarantee the reliable performance of ARAIM have been suggested. User algorithm input parameters (including URA/SISA, URE/SISE, and the probability of satellite or constellation-wide failures) drive the performance of the ARAIM concept.
The essential question now is how to determine these parameters sufficiently from a safety perspective for every GNSS constellation contributing to the ARAIM solution — without being too conservative (thus penalizing service availability), without being too optimistic (thus jeopardizing safety), and with a minimum level of investment at the infrastructure level.
Reliance on past GNSS observations and their extrapolation into the future may not be enough to determine these parameters. As we all know, a GNSS is not at all a steady-state system, as evolutions take place within all elements. Macrocosmically, this includes the evolutions of satellite capabilities materializing, for example, in the different blocks of GPS satellites or major upgrades at the ground segment level with the future transition from OCS to OCX. We might well see similar evolution scenarios for the other GNSS in the future, too.
At a microcosmic scale, changes may occur at the satellite/ground segment level even more frequently and completely invisible to the end-user (for instance, the switch from nominal payload units to redundant ones). For all these reasons past performance may not be easy to extrapolate into the future.
Service performance specifications issued by the GNSS service provider, such as those established by the Department of Defense for GPS, are an excellent place in which to establish the necessary confidence in the service quality and are very helpful during the definition phase of an ARAIM system.
How legally binding such specifications may be and the consequences in case they are not met at some point in the future remain open questions that need further attention. Nonetheless, these types of specifications may be useful as the basis for setting prerequisites for a GNSS to enable in a subsequent step the ARAIM system components needed to estimate guaranteed performance figures.
The necessity for dedicated ground installations is becoming more and more obvious. An ARAIM-specific ground segment is needed to provide users with relevant ARAIM algorithm input parameters sufficient to guarantee the system from a safety perspective. This will be ensured by allocating a proper design assurance level to every threat barrier within the ARAIM ground segment.
The definition of an ARAIM ground segment is the essential missing element and dedicated research activities on this subject are currently ongoing.
Possible Implementation of a Cooperative ARAIM Integrity Service Message Network. Because short-term anomaly detection is covered on the user side by the ARAIM algorithm, the Integrity Service Message (ISM) only has to cover the long-term variations of the signal. Consequently, low update rates of the ISM are acceptable.
As of today, plans call for the ISM to contain information about SISA, SISE, maximum nominal bias, and the probabilities of single-satellite and constellation-wide faults. The dissemination of a validated navigation message through the ISM may also be considered in the future.
Proposed ISM network channels include transmission via the GNSS constellations themselves, drastically limiting the maximum data rate available. Another option could be the use of an upgraded SBAS that, in addition to the augmentation signal, also transmits the ISM.
Both options have the advantage of using pre-existing data channels that would avoid the costly upgrade of hardware at the user side. The option to disseminate ISM through SBAS data links would have the added value that the dissemination of this safety-of-life–related message is carried out through a system designed according to relevant safety requirements.
Apart from the technical challenges of the ISM delivery, political burdens may also appear. Today, integrity services are provided by the countries that each system covers. With an ARAIM system being implemented, it could easily happen that one Air Navigation Service Provider (ANSP) delivers the ISM to a flight that then passes through the jurisdiction of another ANSP. This could lead to questions regarding liability, which need to be investigated.
Another decision must be made as to whether each constellation shall be monitored by an independent ISM checking network. As with SBAS, ARAIM depends on a network of sensor stations in order to generate and verify the ISM. However, the number of necessary stations for ARAIM operations is much smaller than for an SBAS.
If ARAIM should eventually be implemented as a successor to SBAS, the already existing SBAS RIMS networks could be used for that purpose but reduced in size (e.g., only 15 stations for EGNOS RIMS). This would result in significant cost reductions.
Figure 5 shows that a reduced set of sensor stations worldwide would be capable of providing a sufficient depth of coverage for a typical GNSS constellation. As can be seen, all satellites would be in view of at least five ground stations except in the polar regions of the southern hemisphere.
With multiple constellations being deployed several scenarios for the ISM checking network could be feasible:
- each constellation is monitored by a dedicated network of sensor stations
- all sensor stations monitor all constellations using the same monitoring equipment, or
- all sensor stations are equipped with independent monitoring systems for each constellation.
Which scenario will finally be selected is going to be based not only on technical but also on political considerations.
Combined use of EGNOS and ARAIM and Transition Scenarios. With two independent integrity concepts available by 2025, it would be interesting to figure out how to make use of both of them so that users always have access to the position solution estimate with the highest integrity.
The EGNOS V3 evolution upgrade includes plans to add the capability to augment the L5 signal of the GPS constellation as well as Galileo signals. Augmentation of GLONASS signals by EGNOS is also being studied as part of the EGNOS V3 upgrade.
Currently, plans do not call for augmenting BeiDou through EGNOS. However, the simulations presented in this article showed that an additional constellation augmented by EGNOS could increase the availability of integrity in the southern hemisphere significantly.
An additional constellation has an even bigger effect on the integrity performance of ARAIM, because it lowers the VPL worldwide. As a consequence, when EGNOS V3 and ARAIM become operational, EGNOS could be used to provide high-quality integrity over Central Europe while a multi-constellation ARAIM was employed for all other user locations. In this way, basic integrity would be available everywhere while covering the Central European region with two redundant systems.
If redundancy is not a driving factor, ARAIM could be implemented to replace SBAS in the long term. The United States and Europe have indicated that they have different plans here. In the short term, EGNOS is going to be extended to provide integrity based on two constellations starting around 2018, whereas the U.S. WAAS is currently not planning to make use of any other GNSS besides GPS. Consequently, the United States seems to have a higher demand for ARAIM because it could improve integrity significantly across CONUS.
The transition from EGNOS to ARAIM in the long term (>2030) could be realized in the following steps:
- ARAIM and EGNOS V3 are fully deployed. EGNOS serves as the primary integrity source for Europe while ARAIM provides basic integrity everywhere else.
- While gaining more and more confidence in the operation of ARAIM, its integrity performance increases to a level where it performs equally well as EGNOS.
- ARAIM becomes the primary source of integrity for the EGNOS coverage area as well. The number of EGNOS RIMS is successively reduced from 41 to 15. EGNOS stays operational both for ISM checking and as a fallback to ARAIM.
The advantage of a transition from EGNOS to ARAIM is mainly a reduction of operational costs because of the following factors:
a) real-time requirements at the ground segment level are not inherent to a user-equipment–based ARAIM architecture
b) SBAS transponders onboard geostationary satellites may eventually become obsolete
c) the number of ground sensor stations could be reduced.
However, at the time of a possible transition, EGNOS would be a trusted and well-performing system that is replaced by a completely new system. Further research is therefore necessary to see how this transition could best be performed in terms of safety, complexity, schedule, and cost.
Conclusion
ARAIM and multi-frequency, multi-constellation SBAS systems perform similarly with respect to improved availability of integrity when the number of constellations increases. ARAIM could possibly decrease the operational cost of providing integrity. However, further research is still needed to evaluate ARAIM in light of the full integrity “tree.”
Disclaimer
The views expressed in this article are solely the opinions of the authors and do not reflect those of the European Space Agency. Any quantitative system characterizations made use of in this paper together with the derived performance estimates are only for ARAIM simulation purposes and need not necessarily represent the performance obtained by the future GNSS systems.
Additional Resources
[1] Blanch, J. (2010), and T. Walter,and P. Enge, “RAIM with Optimal Integrity and Continuity Allocations Under Multiple failures,” IEEE Transactions on Aerospace and Electronic Systems, Volume: 46, Number: 3, pp. 1235–1247, July 2010
[2] Blanch, J. (2011), and T. Walter, P. Enge, S. Wallner, F. Amarillo Fernandez, R. Dellago, R. Ioannides, B. Pervan, I., Fernandez Hernandez, B. Belabbas, A. Spletter, A., and M. Rippl, “A Proposal for Multi-Constellation Advanced RAIM for Vertical Guidance,” The Proceedings of the ION GNSS 2011, Portland, Oregon USA, September 2011
[3] Brenner, M., “Implementation of a RAIM Monitor in a GPS Receiver and an Integrated GPS-IRS,” Proceedings of the Third Technical Meeting of the Satellite Division of The Institute of Navigation, Colorado Springs, CO, pp. 397-406, 1990
[4] Brenner, M., “Integrated GPS/Inertial Fault Detection Availability,” Proceedings of The Institute of Navigation 8th International Technical Meeting, Palm Springs, CA, September 1995
[5] Brown, R. G., and P. Y. C. Hwang, “GPS Failure Detection by Autonomous Means Within the Cockpit,” Proceedings of the Annual Meeting of The Institute of Navigation, Seattle, Washington USA, pp. 5–12, June 24–26, 1986
[6] Brown, R. G., and P. W. McBurney, “Self-Containded GPS Integrity Check Using Maximum Solution Separation as the Test Statistic,” Proceedings of the First Technical Meeting of the Satellite Division of The Institute of Navigation, Colorado Springs, Colorado USA, pp. 263–268, 1987
[7] Ene, A., “Utilization of Modernized Global Navigation Satellite Systems for Aircraft-based Navigation Integrity,” Dissertation, Department of Aeronautics and Astronautics, Stanford University, California USA, March 2009
[8] Federal Aviation Administration, Phase II of the GNSS Evolutionary Architecture Study, February 2010
[9] International Civil Aviation Organization, Aeronautical Telecommunications, in Annex 10 to the Convention on International Civil Aviation International Standards and Recommended Practices (SARPs), Volume I (Radio Navigation Aids), Montreal, Canada, July 16, 2007
[10] International Civil Aviation Organization, Safety Management Manual (Doc. 9859), Second Edition, Montreal, Canada, 2009
[11] Lee, Y. C., “Analysis of Range and Position Comparison Methods as a Means to Provide GPS Integrity in the User Receiver,” Proceedings of the Annual Meeting of The Institute of Navigation, Seattle, Washington USA, June 24–26, pp. 1–4, 1986
[12] Lee, Y.C., “Feasibility Analysis of RAIM to Provide LPV-200 Approaches with Future GPS,” Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation, Fort Worth, Texas USA, September 25–28, pp. 2898–2910, 2007
[13] Lüken, T., and E. Groll, F. Antrack, and B. Korn, “Helicopter IFR Steep and Curved Approaches Using SBAS Guidance,” 34th European Rotorcraft Forum, Liverpool, United Kingdom, September 16–19, 2008
[14] Matlab Algorithm Availability Simulation Tool
[15] Parkinson, B. W., and P. Axelrad, “A Basis for the Development of Operational Algorithms for Simplified GPS Integrity Checking,” Proceedings of the First Technical Meeting of the Satellite Division of The Institute of Navigation, Colorado Springs, Colorado USA, pp. 269–276, 1987
[16] Parkinson, B. W., and P. Axelrad, “Autonomous GPS Integrity Monitoring Using the Pseudorange Residual,” Navigation (Washington), Volume: 35, Number: 2, pp. 255–274, 1988
[17] RTCA, Inc., Minimum Operational Performance Standards for Airborne Supplemental Navigation Equipment Using Global Positioning System (GPS), Document No. RTCA/DO-208, prepared by SC-159, Washington D.C., July 1991
[18] RTCA, Minimum Operational Performance Standards for Global Positioning System/Wide Area Augmentation System Airborne Equipment,” RTCA Publication DO-229D, 2006
[19] U. S. Department of Defense, Global Positioning System Standard Positioning Service Performance Standard, 4th edition, September 2008
[20] U. S. Department of Transportation, Federal Aviation Administration (FAA), TSO-C129a, “Technical Standard Order, Airborne Supplemental Navigation Equipment Using Global Positioning System (GPS),” Washington DC, 1992
[21] Walter, T., and J. Blanch, and JP. Enge, “Vertical Protection Level Equations for Dual Frequency SBAS,” Proceedings of the 23rd International Technical Meeting of the Satellite Division of The Institute of Navigation, Portland, OR, pp. 2031-2041, September 21-24, 2010
[22] Walter, T., and P. Enge, “Weighted RAIM for Precision Approach,” Proceedings of the 8th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS-95), Palm Springs, California USA, pp. 1995–2004, September 12–15, 1995
[23] Walter, T., and A. Hansen, and P. Enge, “Message Type 28,” Proceedings of the ION NTM 2001, Long Beach, California USA, January 2001
