A frequently asked question about GPS is: How accurate is a GPS-based position? The experienced GPS user knows that a big difference lies between using pseudoranges alone or combining pseudoranges and carrier phases.
The following analysis is partly based on an idea raised in the book, Global Positioning System: Signals, Measurements, and Performance, by P. Misra and Per Enge (See Additional Resources section at the end of this article).
A frequently asked question about GPS is: How accurate is a GPS-based position? The experienced GPS user knows that a big difference lies between using pseudoranges alone or combining pseudoranges and carrier phases.
The following analysis is partly based on an idea raised in the book, Global Positioning System: Signals, Measurements, and Performance, by P. Misra and Per Enge (See Additional Resources section at the end of this article).
In order to get a quantitative answer to the question Kostas Dragūnas, a research assistant at the Danish GPS Center and now an Aalborg University Ph.D. student, recorded data simultaneously with a master and a rover receiver.
In order to vary the receiver equipment, we used two dual-frequency L1/L2 GPS receivers that were different from the models employed in previous EASY Suite field campaigns. These receivers store data in a binary format called the GPS Receiver Interface Language (GRIL).
The following message was sent to the receivers before starting the observation session:
dm
em,,/msg/jps/GT,SI,R1,P1,R2,P2
Time of start was 481,860 seconds and the final epoch was at 484,395 seconds; so, 2,535 synchronous epochs of observations were recorded with a one-second epoch interval. We deleted 95 epochs because of missing data at either the rover or the master, or repeated estimation of ambiguities. This makes a continuous record of about 40 minutes.
The original observations were modified in several ways. After each ephemeris, the master receiver issued two subsequent P2 (full P/L2 carrier phases) messages (binary identical), Subsequently, the rover receiver sometimes issued two GPS Time (GT) messages — wn and tow (binary identical).
easy15 assumes data arriving in real-time from the two receivers. In reality, we read from two files, 19jan07m.log and 19jan07r.log, containing a mixture of observations and ephemerides. The baseline is about 1,509.3 meters long.
The actual reading of the log-files is done by the readGrilM and readGrilR functions. We are using two similar codes for reading in each log-file in order to avoid too much “bookkeeping” about where to read binary data in the files. A typical reading contains information on time of week, tracked satellites (identified by pseudorandom noise codes or PRNs), and observed pseudorange and carrier phase on the two frequencies.
The reading is complicated by the fact that new ephemerides may appear at any time in-between the observations. The ephemerides are stored in a global matrix, EPH. Any time a new version of an ephemeris arrives, it overwrites the old one.
As mentioned, we read from two stored files; therefore, we first have to determine the first epoch common to both receivers. Next, we determine the number of tracked PRNs at both master and rover sites for which we know the ephemerides.
When the number of common PRNs is four or more, we compute the master position using the recposRTK function, and all elevation angles as seen from here. We delete low-elevation PRNs and select a reference PRN. Next all observations are rearranged so that master and rover data match each other — the sequence of PRNs in the master and rover receivers are likely to be different.
Ambiguities are estimated using Clyde Goad’s method as described in the text by G. Strang and K. Borre, page 490, cited in Additional Resources.
New PRNs most often rise at different epochs at the master and rover. Hence, we need to omit the observations from one receiver until the PRN appears with complete data at both receivers.
We repeat the computation of the master position with good PRNs and find the ellipsoidal height hi needed for the later computation of tropospheric delay.
We choose a Kalman filter where the state vector x has three components, namely, the baseline components (x,y,z). We initialize the covariance matrices for the vector of observations ∑e,k, for the system equations ∑ε,k, and for the state vector P0|0.
Note: users should realize that a Kalman filter and its innovation vector may run smoothly and the baseline components may still be wrong. A correct ambiguity estimation leads to excellent estimates of the baseline components. Incorrect ambiguity estimates definitely lead to incorrect estimates of the baseline components while the filter works intensively on obtaining small innovations that try to push the baseline components to the correct values.
Next we read one epoch of data in the master file and in the rover file, prepare the double differenced observations, correct for tropospheric delays, and then set up the innovation vector b – Ax. We update the filter, plot the result in an open figure window, and proceed to the next epoch.
This code is the closest we get to a real-time kinematic (RTK) code without having two receivers connected directly to the laptop computer’s com port. If the receivers/laptop configuration can be achieved, then a user may set up the ports using the I/O facility. For one port the following code reads a data stream from the receiver into the file legacy.tex:
s = serial(‘COM2’);
s.OutputBufferSize = 512;
s.InputBuffersize = 50000;
fopen(s);
s.BaudRate = 9600;
set(s,’TimeOut’,1);
s.RecordMode = ‘index’;
s.RecordDetail = ‘verbose’;
s.RecordName = ‘legacy.tex’;
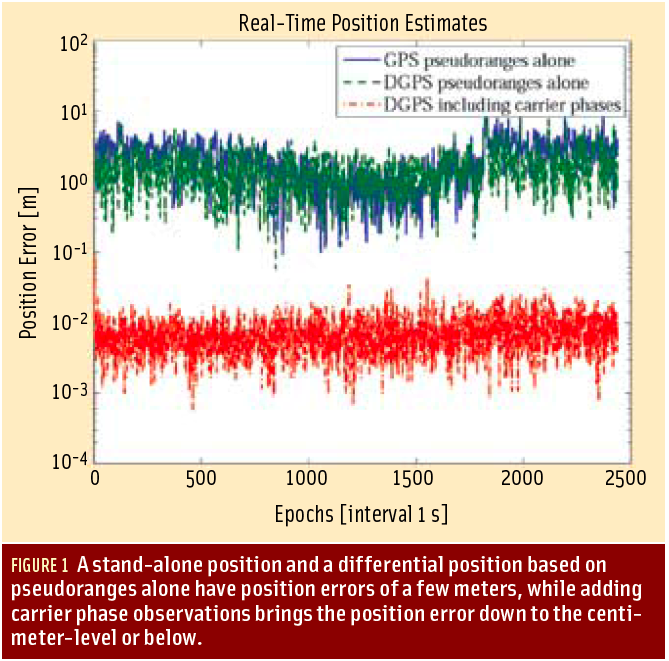
Figure 1 illustrates two levels of positioning accuracy obtained from GPS in real-time with position errors ranging from several meters to centimeters. The norm of the position error is plotted for observations taken at one-second intervals over a period of about 42 minutes.
The raw L1 pseudorange position accuracy is typically a few meters. Access to concurrent pseudorange observations from a GPS master receiver (at a known location) does not reduce the errors significantly; possibly it eliminates some common trends in the positions.
Finally, the full potential of the observational data is exploited by including both pseudoranges and carrier phase observations to obtain position estimates at the centimeter-level or better.
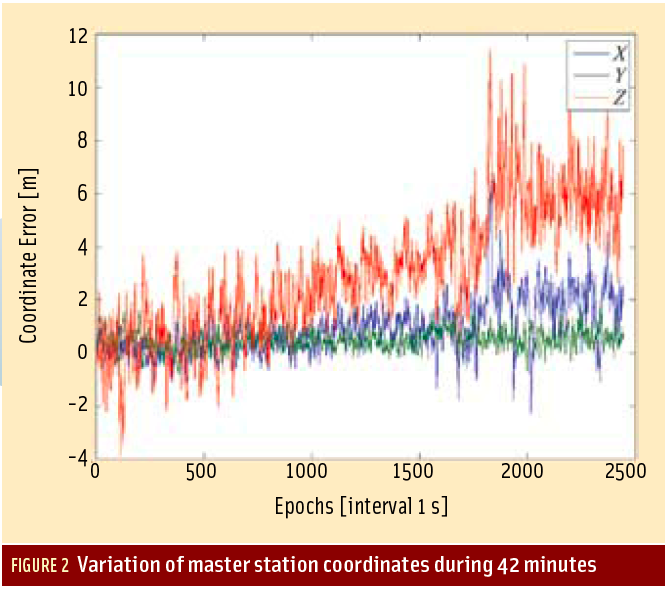
Figure 2 shows the variation over 42 minutes of master station coordinates as computed from pseudoranges alone. Typically, the X and Y coordinates show a lesser variation than the Z coordinate (for Aalborg, Denmark).
Additional Resources
[1] Misra, P. and P. Enge, Global Positioning System: Signals, Measurements, and Performance, 2nd edition, Ganga-Jamuna Press, Lincoln, Massachusetts, USA, 2006
[2] Strang, G. and K. Borre, Linear Algebra, Geodesy, and GPS, Wellesley-Cambridge Press, Wellesley, Massachusetts, USA, 1997