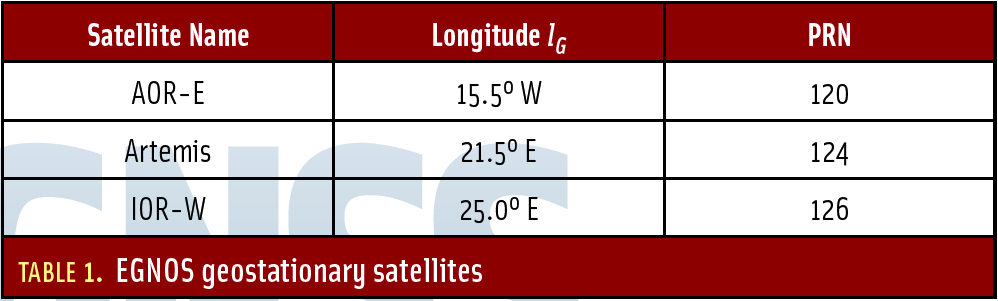
 Table 1: EGNOS geostationary satellites.
Table 1: EGNOS geostationary satellites.Some GPS applications generate long time series of position estimates. Most often, an easy way of getting a quick overview on the recorded data is to plot them. However, it may be difficult from a plot to quantify statistical measures such as mean value, standard deviation, and circular error probable (CEP).
Some GPS applications generate long time series of position estimates. Most often, an easy way of getting a quick overview on the recorded data is to plot them. However, it may be difficult from a plot to quantify statistical measures such as mean value, standard deviation, and circular error probable (CEP).
easy14 continues the aviation-oriented discussion begun in the July/August 2009 issue of Inside GNSS (Easy Suite II, Part 3), drawing on use of the European Geostationary Navigation Overlay Service (EGNOS), a satellite-based augmentation system (SBAS). The files for the corresponding MATLAB codes can be found on-line; details included in the Additional Resources section near the end of this article.
Our demonstration sample uses data collected on August 20, 2008, over a 4.2-hour period with a static GPS L1 receiver with 12 code and carrier channels and two optional SBAS channels, located at a site south of Aalborg, Denmark. This receiver is a commercial one capable of handling EGNOS data. However, dedicated EGNOS receivers exist that exploit the data optimally and from which better-looking plots can be generated.
The EGNOS-corrected positions were computed by using a MATLAB implementation done at the Danish GPS Center (DGC). For a given alert limit a, EGNOS provides an integrity measure that tells the user to use or not to use the position in question.
The EGNOS corrections can be obtained in several ways: directly via the geostationary satellites listed in Table 1 (above), or from a service called Signal in Space through the Internet (SISNeT), or through other services. In the present case we apply a postprocessing mode which relies on the EGNOS Message Server (EMS) on-line at ftp://131.176.49.48/pub/
In polar regions users may have difficulties in receiving signals from the geostationary satellites and, hence, the Internet version becomes useful. However, the Internet is not available near the poles too often!
We shall make a small digression to investigate the magnitude of the elevation angle h of a (geostationary) satellite as a function of the receiver site.
. . .
The EGNOS information allows us to correct the observed pseudoranges for atmospheric delays and other error sources. A fast EGNOS correction is computed from navigation messages 2–5 that contain the so-called fast data set. The message starts with the 2-bit issue of data PRN (IODP), an 8-bit preamble, a 6-bit message type identifier (values can be 2, 3, 4, or 5), and a 2 bit issue of data fast (IODF).
Next follows the fast data set for 13 satellites: 12 bits for the fast pseudorange correction PRC and 4 bits for the user differential range error indicator (UDREI). The message ends with 24 parity bits, in total 250 bits. The fast data set for the next 13 satellites is contained in the following message and so forth.
The PRC value is given in the interval [-256.000, +255.875] with a resolution of ⅛ meter.
The range-rate correction RRC of the fast correction is computed as the difference between the current PRC and the previous one divided by the time interval between the two values. The time of applicability tof is identical to the transmission time of the first bit in the message.
. . .
Contemporary positioning theory uses the following four concepts that enter into almost every aviation specification: accuracy, integrity, continuity, and availability.
The first concept, accuracy, fits our intuition well as it measures the difference between the (corrected) computed position and the true position. An SBAS implementation is obliged to quantify the accuracy of a wide-area differentially corrected position solution. Accuracy may be estimated by the difference between a receiver position and the true position which, for CEP 95%, is only exceeded 5 percent of the time in the absence of system failures.
Integrity risk is defined as the probability that the SBAS exceeds either the horizontal or vertical alert limits (HALs or VALs) and the system alert is silent beyond the time-to-alarm. EGNOS has been designed for a six-second time-to-alarm.
Continuity and availability are expressed in global terms. If a user experiences a system outage due to signal blockage, from a global perspective this is not a loss in continuity of the system — it is a local phenomenon.
Clearly, we need to distinguish between issues related to availability and continuity and what is availability of the system from a user’s perspective.
. . .
Availability can only be associated with geostationary satellites. For users employing the Internet to obtain the EGNOS information, everything changes. In the present study we use EMS and not the real-time service SISNeT . . .
For the complete story, including figures, graphs, and images, please download the PDF of the article, above.
Acknowledgment
Kostas Dragūnas added several changes to the original M-files vplstat and hplstat written by Todd Walter of Stanford University. The files are included in the Easy Suite II files (see Additional Resources) with the permission of Stanford University. Users also need the bound2 file in the download directory.
Corrections to easy13
In the EASY Suite II installment in the July/August 2009 issue of Inside GNSS (Easy Suite II, Part 3), in Figures 1 and 4, the expression “protection level α” should have been “protection level a.”
In easy13.m the Matlab code is missing the F matrix (the transformation matrix from ECEF to ENU) in the expression for M. Hence the alpha values and HPL are wrong. Consequently Figure 3 is valid for δxXY and not δxEN as stated on the vertical axis.
On page 49 of the article in the paragraph following equation (10), Mo = M(1:2,1:2) should be Mo = M(1:2,:).
Additional Resources
[1] The original Easy Suite can be found online at http://kom.aau.dk/~borre/easy/. The complete set of Easy Suite II Matlab codes can be found in compressed (“zipped”) files at http://gps.aau.dk/~borre/easy2.
[2] RTCA, Inc. (formerly Radio Technical Commission for Aeronautics), RTCA/DO-229C, Minimum Operational Performance Standards for Global Positioning System/Wide Area Augmentation System Airborne Equipment, 2001
[3] Strang, G., and K. Borre, Linear Algebra, Geodesy, and GPS, Wellesley-Cambridge Press, Wellesley, Massachusetts USA, 1997




