The usual formulation of position determination involves four unknowns: three physical dimensions (X,Y,Z) and the satellite-receiver time offset. In cases where we can observe five or more pseudoranges, one might well ask if the redundant pseudoranges could be used to check the consistency among the observations —the fundamental principle behind receiver autonomous integrity monitoring (RAIM).
The usual formulation of position determination involves four unknowns: three physical dimensions (X,Y,Z) and the satellite-receiver time offset. In cases where we can observe five or more pseudoranges, one might well ask if the redundant pseudoranges could be used to check the consistency among the observations —the fundamental principle behind receiver autonomous integrity monitoring (RAIM).
easy13 describes a technique for coping with this situation. In so doing, key concepts such as horizontal and vertical protection levels (HPL and VPL) are introduced. Necessarily, we also have to introduce some theory that motivates the procedures. (We will return to this topic with some further graphical illustrations in easy14.)
RAIM is a major technique for GNSS in many safety-critical applications. It has been with us since about 1990. Much of the material presented in the following relies on the work by B. Pervan cited in the Additional Resources section near the end of this article.
. . .
At http://www.nstb.tc.faa.gov/Terms.html readers may find the following definition of HPL: The Horizontal Protection Level is the radius of a circle in the horizontal plane with its center being at the true position which describes the region that is assured to contain the indicated horizontal position.
. . .
Under a normal condition (NC), the position error ||δx|| does not exceed the protection level a, and the residual is smaller than the threshold R, as in case III. If the position error does not exceed the protection level a, but the residual is larger than the threshold R, a false alarm (FA) has occurred, which is case IV.
When both protection level and residual threshold have been breached, a detection failure (DF) has occurred — case I. Finally, a missed detection (MD) happens when the position error ||δx|| is larger than the protection level a, but the residual is smaller than the threshold R; that is case II.
. . .
Input to RAIM: The variance σb2 of a pseudorange observation, the coefficient matrix A of the linearized least-squares observation equations, and the maximum allowable probabilities for a false alarm P(FA) and a missed detection P(MD).
Output of the algorithm: Horizontal protection level (HPL), which is the radius of a circle, centered at the true position that is assured to contain the indicated horizontal position with the given probability of false alarm and missed detection.
Similarly for Vertical Protection Level (VPL). Again, an official definition (at http://www.nstb.tc.faa.gov/Terms.html) is: The vertical protection level is half the length of a segment on the vertical axis with its center being at the true position, which describes the region that is assured to contain the indicated vertical position.
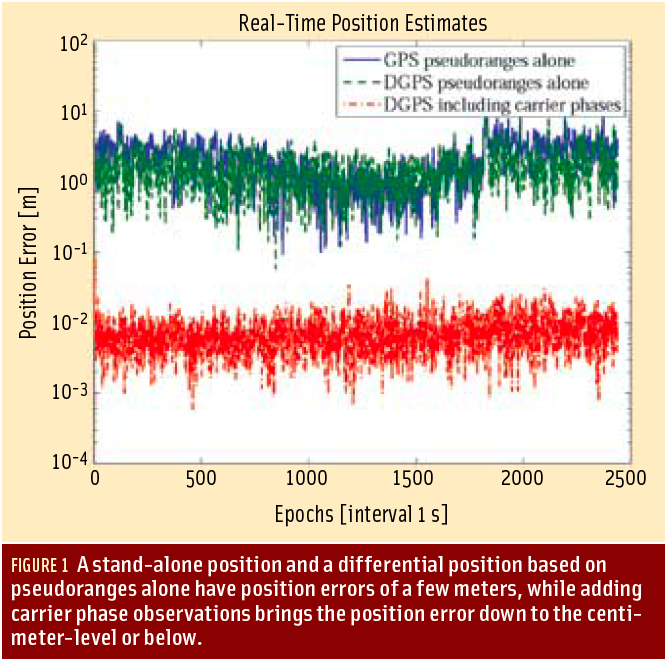
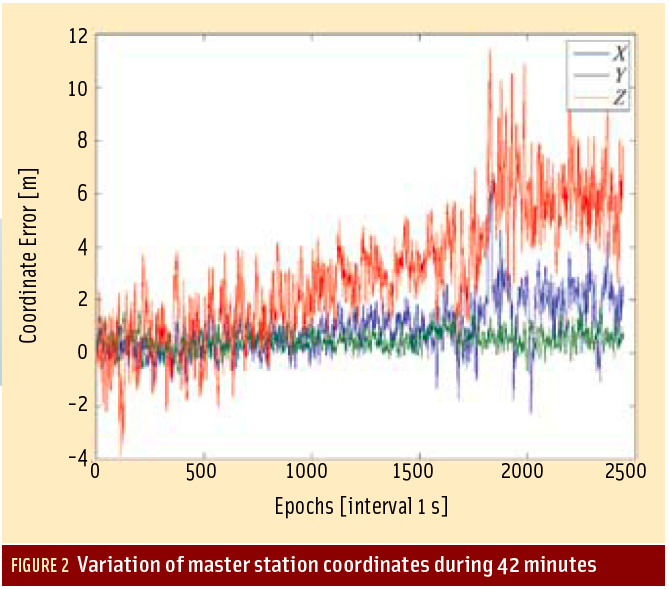
For the complete story, including figures, graphs, and images, please download the PDF of the article, above.
Additional Resources
[1] The original Easy Suite can be found online at http://kom.aau.dk/~borre/easy/. The complete set of Easy Suite II Matlab codes can be found in compressed (“zipped”) files at http://gps.aau.dk/~borre/easy2.
[2] Brown, R. G., and P. Y. C. Hwang, Introduction to Random Signals and Applied Kalman Filtering, third edition, John Wiley & Sons, Inc., New York, 1997
[3] de Jong, K., “Real-time integrity monitoring, ambiguity resolution and kinematic positioning with GPS,” Proceedings of 2nd European Symposium on GNSS’98, Toulouse, France, pp. VIII07/1-VIII07/7, 1998
[4] Kaplan, E., and C. J. Hegarty (editors), Understanding GPS, Principles and Applications, second edition, Artech House, Boston and London, 2006
[5] Nikiforov I., and B. Roturier, “Advanced RAIM algorithms: First results,” ION GNSS2005, 18th International Technical Meeting of the Satellite Division of the Institute of Navigation, Long Beach, California, USA
[6] Pervan, B. S., Navigation Integrity for Aircraft Precision Landing Using the Global Positioning System. Stanford University, Stanford, California, USA, 1996