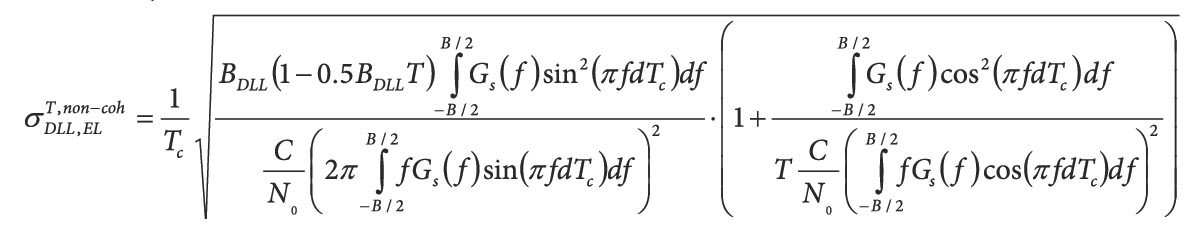Equations 1 – 7Working Papers explore the technical and scientific themes that underpin GNSS programs and applications. This regular column is coordinated by Prof. Dr.-Ing. Günter Hein, head of Europe’s Galileo Operations and Evolution.
Working Papers explore the technical and scientific themes that underpin GNSS programs and applications. This regular column is coordinated by Prof. Dr.-Ing. Günter Hein, head of Europe’s Galileo Operations and Evolution.
Several advanced services rely on Global Navigation Satellite System (GNSS) receivers as data providers. GNSS-derived position, velocity, and time (PVT) information enables applications such as proximity-based marketing, real-time travel services, traffic updates, precision farming, weather reports, and roadside assistance, to mention a few examples.
GNSS receivers also play a significant role in several regulated applications where security is an important aspect. In the road transportation sector, the new EU Regulation 165/2014 (see European Commission in Additional Resources) adopted in February 2014 by the European Parliament and the Council foresees the introduction of a new generation of Digital Tachographs (DTs), called “smart tachographs,” with increased security mechanisms, a GNSS component, and different communication interfaces. Tachographs record driving time and mitigate the risk of tired drivers having looser control of vehicles with higher risk of accidents. There are potential economic incentives for infringement of the regulation and tampering with the tachograph system. In this respect, the secure provision of PVT information from a trusted GNSS receiver is an important asset.
Integrated in smartphones, GNSS receivers can also be used to increase the security of mobile banking services (see A. Pujante in Additional Resources). In addition, there may be economic interests around smartphone usage to falsify the data provided by a GNSS receiver.
In this respect, GNSS receivers can be interpreted as nodes in a network where they provide location data to higher service levels. In the tachograph, the vehicle unit, i.e., the recording equipment installed in the commercial vehicle to monitor the driver behavior, implements and provides these higher service levels. In smartphones, these levels are the final user applications: electronic fraud can take advantage of possible vulnerabilities of the communication channel between GNSS receivers and higher service levels. In particular, GNSS Faking Software (GFS) applications can be installed on the smartphone to falsify the user position with the final goal of obtaining a personal or commercial benefit.
GNSS data faking consists of intercepting genuine GNSS data and replacing them with forged location information. Differently from jamming and spoofing, which operate at the Signal-in-Space (SiS) level, GNSS data faking operates at the receiver level. GNSS data faking tries to intercept and falsify the messages between the GNSS receiver and the application nodes.
In GNSS spoofing, an attack can be detected by exploiting SiS-specific features which are difficult to counterfeit (see A. Jafarnia-Jahromi et alia in Additional Resources). Similarly, a possible solution to GNSS data faking is the usage of device-specific features which are difficult to counterfeit. This approach is usually referred to as device fingerprinting and is defined as “the process of gathering device information to generate device-specific signatures using them to identify individual devices” (Q. Xu et alia, Additional Resources). Fingerprinting has gained significant interest in the field of wireless networks where node forgery or impersonation has become a threat. Node forgery consists of the acquisition of legitimate credentials by an adversary who will use them to conduct fraudulent activities. GNSS data faking is similar to node forgery in a wireless network.
In particular, a simulator or another device can be used to impersonate an actual GNSS receiver. In this way, misleading PVT information can be sent to the final PVT user. GNSS receiver fingerprinting can be adopted in security- enhanced applications that will be able, at least to a certain extent, to verify the authenticity of GNSS data. In such applications, the device which relies on GNSS data, such as the vehicle unit of the tachograph, will also extract from the received GNSS messages unique features which could be used to validate the identity of the GNSS receiver by comparing it to the previously recorded data. In a potential deployment scenario for the DT, the vehicle unit could record the fingerprints of the GNSS receiver in the initial installation phase or during the periodic calibration checks (e.g., every two years as defined by the regulation). The installation and calibration phases are executed in a controlled environment (e.g., workshop) where the identity of the GNSS receiver can be checked by the installer.
The first step in device fingerprinting is the selection of appropriate features, which should satisfy two basic properties: the features should be difficult to counterfeit and be stable with respect to environmental changes.
We investigate the selection of appropriate features for GNSS receiver fingerprinting. This process consists of considering, at first, a set of redundant metrics that have the potential to identify the receiver. A fingerprint, i.e., a subset of the original set of metrics, is then selected using a filtering approach.
We first investigate metrics related to the receiver clock, summarizing the results obtained by the authors in the paper presented at the 2016 ION GNSS+ conference and listed in Additional Resources. We then extend the analysis to clock-unrelated features.
Clock-Based Metrics
Fingerprinting of electronic devices is often based on distinctive imperfections such as the errors generated by the local oscillator of the device under test. In the context of wireless networks, Radio Frequency (RF) oscillator imperfections have been used as a source of reliable, forge-resistant features (see, for example, A. C. Polak and D. L. Goeckel in Additional Resources).
Consider for example, the normalized frequency error shown in Figure 1. The time series have been obtained by normalizing the receiver clock drift estimated as part of the navigation solution of a GNSS receiver and shows distinctive random effects with (possibly) stable characteristics. These characteristics must be identified and used as features.
We analyzed several metrics that are adopted in the literature to characterize the behavior of a time/frequency source.
The metrics considered are illustrated in Figure 2 that also describes the main elements of the methodology adopted for their evaluation. GNSS measurements are used to compute the user PVT solution. The normalized receiver frequency error, fe[n], is then computed from the clock bias, dtr[n], as
Equation (1) (for equations, see inset photo, above right)
here n is the time index and Ts is the sampling rate. fe[n] can also be computed by normalizing the clock drift by the GNSS center frequency, in this case fL1=1575.42 MHz. The time series shown in Figure 1 have been obtained by normalizing the clock drift estimated during a static data collection. It is noted that the clock drift and the clock bias are computed from different observables, Doppler measurements, and pseudoranges. Thus, they have different characteristics. We showed in our paper presented at the ION 2016 GNSS+ conference that the normalized frequency error derived from Doppler measurements leads to the features that are more stable to environmental changes. Doppler measurements are less affected by the different error sources and thus should be preferred for the determination of receiver features.
The normalized frequency error is then used to compute different metrics such as the Allan Deviation defined as (see S. Bregni, Additional Resources):
Equation (2)
Equation (3)
The Allan Deviation is a curve which depends on the averaging time, τ. For this reason, it cannot be used directly as a feature for fingerprinting. Therefore, summary statistics, describing the behavior of the Allan Deviation are needed. We selected the Allan Deviations at τ = 1 second and at τ = 30 seconds, the curve slope between τ = 1 second and τ = 30 seconds, the minimum value, and the averaging time corresponding to the minimum Allan Deviation. In this way, five features where obtained from the Allan Deviation.
A similar process was undertaken for other performance curves that are generally used for characterizing time and frequency sources. We considered the Root Mean Square Time Interval Error (RMS-TIE), the Maximum Time Interval Error (MTIE), and the correlation between the samples of the normalized frequency error. As for the Allan Deviation, summary statistics were selected. In this way, a total of 13 features were determined. Additional details on the different features selected can be found in D. Borio et alia.
Clock-Unrelated Metrics
Many mass-market receivers only provide the user location and velocity. In this case, it is not possible to compute the clock-based metrics discussed above. For this reason, we considered clock-unrelated features for receiver identification. The term “clock-unrelated” is used to denote features derived from the position and velocity time series, i.e., from data that do not include the receiver clock bias and clock drift. The rationale behind the analysis conducted is that the errors affecting the clock components and the vertical components in the navigation solution should, in general, be highly correlated. In this way, it should also be possible to extract effective features for receiver fingerprinting from the spatial components of the navigation solution.
We followed an approach similar to that detailed for the clock-related features. In particular, the features described in the previous section were computed using velocity and position components. For example, the Allan Deviation is computed using the velocity time series. In this case, the Allan Deviation does not characterize the stability of the receiver oscillator but determines the quality of the velocity solution.
From the analysis conducted, it emerged that clock-unrelated features are not, in general, strongly related to their clock-based counterpart. Figure 3 compares the Allan Deviations computed using the different PVT components for two different receivers. The left column of the figure considers Allan Deviation curves computed using Doppler-based time series. Since velocity components and clock drifts have different normalizations, the curves have been shifted in order to make the initial point of each plot coincide. In particular, the Allan Deviations were shifted to start at one. A good match between Allan Deviations is found between the different curves for τ ∈ [1 – 100] for the one receiver considered in the top row of Figure 3. The same result, however, is not true for the other receiver considered in the bottom row. Although a better match is found when considering pseudorange-derived metrics (see right column of Figure 3), clock-unrelated metrics convey, in general, different information than their clock-based counterparts. Thus, the results obtained from the clock bias and drift cannot be directly applied to features extracted from position and velocity time series.
Filtering and Feature Selection
After selecting a redundant set of candidate features, it is necessary to apply a selection process in order to determine the most effective subset of features for classification. Feature selection algorithms are broadly classified as filter and wrapper methods (see the review paper from G. Chandrashekar and F. Sahin, Additional Resources). The former approaches use a cost function to rank the different subsets of features. The latter techniques wrap the selection process around a classifier/predictor, i.e., the final “user” of the subset of features selected. In particular, wrapper methods select the subset of features with the highest classification performance.
We adopted a filter approach as a compromise between complexity and performance. To apply the filtering approach, it is first necessary to preprocess the time series obtained from the GNSS receivers. The pre-processing applied here is briefly summarized in Figure 4. The time series collected for the feature computation are first segmented into data blocks of limited duration. Each segment of data will be used for computing a different realization of the metrics described above. In this way, several realizations of feature vectors are obtained. Note that several receivers of different models have been used for the analysis described in the next sections. Each receiver model represents a class. In this way, several realizations of the feature vectors are obtained for the different classes. The components of the feature vectors are heterogeneous and can assume significantly different values. Thus, a normalization is required. The following normalization is used here:
Equation (4)
where χjk denotes the jth realization of the kth feature. The overline notation is used to denote normalized quantities. In the following, an additional index will be used to denote membership to a specific class or receiver type. The maximum and minimum values are obtained considering all the feature realizations from all receiver classes. Using Equation (4), normalized feature vectors are obtained where each component takes values within the [0, 1] range.
After data pre-processing, feature filtering is applied. The score function considered here is
Equation (5)
where F denotes the subset under analysis and di,j(F) is the inter-class distance between classes i and j. di,j(F) is the intra-class distance of the ith class. The intra- and inter-class distances are defined in terms of normalized features (4). In particular, the intra-class distance is defined as
Equation (6)
Equation (7)
and describes the average distance between two classes. Figure 5 provides a geometric interpretation of the different quantities defined here. It emerges that score function (5) is the ratio between the minimum distance between classes and the larger class size. Thus, subset F is selected in order to maximize the spread between classes and minimize the class dimensions.
Experimental Setup
The theoretical framework described in the previous sections has been implemented and tested using the data collected during two data collections. The tests were performed in different weeks and in different signal conditions. Two different scenarios were selected in order to evaluate the feature stability to environmental changes.
The first test was conducted using a geodetic antenna located on the European Microwave Signature Laboratory (EMSL) at the Joint Research Centre (JRC) premises in Ispra, Italy. The EMSL is the highest building in the area and no obstacles are present around the antenna. Hence, the first test was carried out in open-sky conditions.
The second test was performed using an antenna mounted on the rooftop of an office building in the JRC campus. In this case, the building is surrounded by taller constructions and by high trees which cause multipath and fading creating a disturbed signal environment.
The locations of the antennas used for the data collection are shown in Figure 6.
A common setup was designed and adopted for the two data collections. In each setup, several receivers were connected to the same antenna using an RF splitter and used to collect almost four days of data for each experiment. The length of each data collection justifies the data segmentation introduced in the previous section. The receivers logged raw GNSS observables, i.e., pseudoranges and Doppler shifts, with a 1 hertz data rate. Different types of receivers were used, including mass-market and professional multi-constellation receivers.
In order to have the same conditions, only GPS measurements were used for the data analysis. Moreover, a common set of ephemerides were adopted for all the receivers. In this way, the same operational conditions were adopted for the different receivers.
The list of receivers used in the two tests is provided in Table 1 along with the number of devices of the same type. The actual model of the devices can be found in the Manufacturers section.
Five GNSS timing modules were used for the two data collections. Among them, one was updated with the latest firmware that enabled the processing of Galileo signals. The update was performed to analyze the impact of firmware changes on devices of the same type.
Experimental Results
The data collected during the two tests described above were used for feature selection. In particular, subsets of two and three elements were considered. For each subset, score function (5) was computed. We considered only features derived from Doppler measurements, i.e., computed from the velocity/clock drift solution, because of the higher stability of these types of observables to errors and environmental changes. The features have been computed using data segments of one hour, i.e., 3,600 elements.
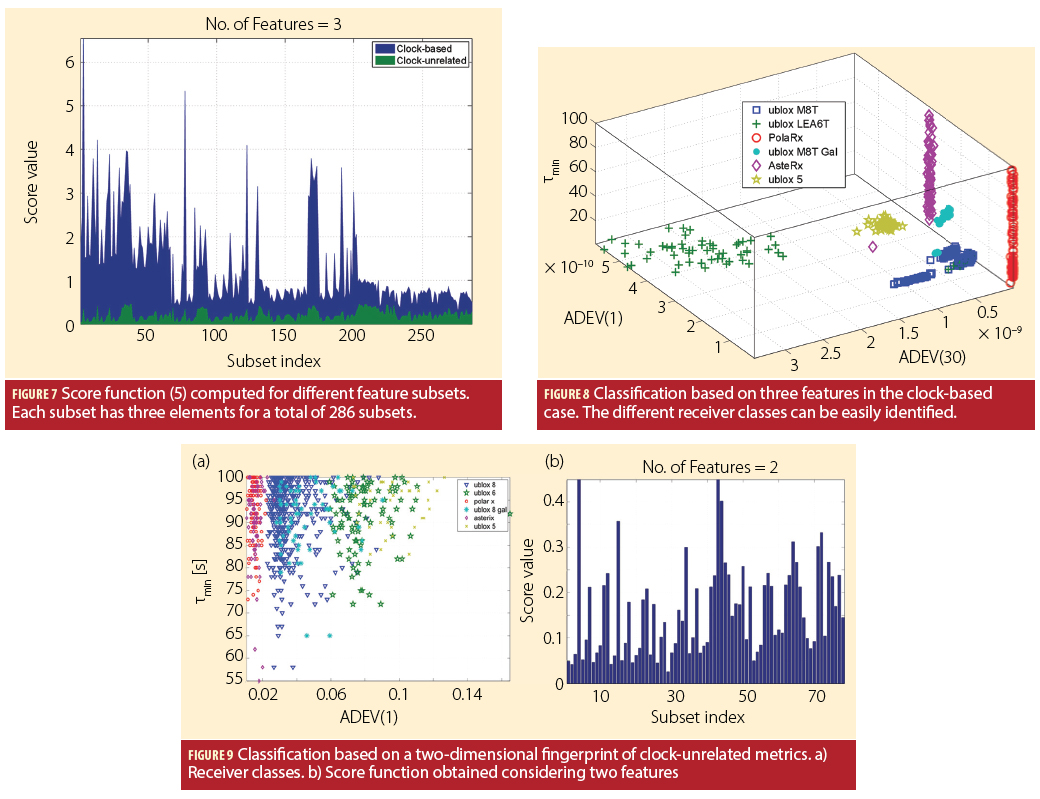
Subsets of three elements are analyzed in Figure 7 where both clock-based and clock-unrelated metrics are considered. In the clock-based case, features are computed from the receiver clock drift. In the clock-unrelated case, the up component of the velocity solution is used. Since 13 features were originally considered, a total of 286 subsets is found. The abscissa in Figure 7 is the index used to enumerate the different subsets of three elements. From the results reported in Figure 7, it clearly emerges that clock-based features significantly outperform their clock-unrelated counterparts. In the clock-based case, the maximum value of the score function is greater than six. This implies that, for the feature subset leading to the maximum of (5), the smallest inter-class distance is more than six times bigger than the largest inter-class distance. In this way, classes/receiver types are clearly separated and effective clustering can be performed.
This fact is further analyzed in Figure 8 showing the clusters formed using the three features leading to the maximum value of (5). These features are all derived from the Allan Deviation curve and are the Allan Deviations at τ = 1 second and τ = 30 seconds, and the averaging time leading to the minimum Allan Deviation value. The different receivers can be easily identified in the feature space depicted in Figure 8. The professional receivers from one manufacturer show enhanced performance in terms of Allan Deviation with respect to mass-market devices. This is expected given the different market segment, i.e., that of professional receivers. Mass-market receiver of type a is the only device showing significantly different behaviors in the two data collections. In the open-sky scenario, this receiver has features similar to those obtained for the timing modules mentioned above. Figure 8 also shows that firmware updates can affect the receiver behavior. This fact clearly emerges when considering the behavior of the one device updated with the Galileo firmware: the cluster defined by the features determined for this device is clearly distinct from that of the standard timing modules.
In the clock-unrelated case, the score function is always lower than 0.5. This implies a significant overlapping between classes in terms of clock-unrelated features. This fact is further investigated in Figure 9 showing feature selection results in the two-dimensional case. Two-dimensional feature vectors are considered here for clarity reasons. When the three-dimensional case is considered, the feature space representation is quite cluttered making the interpretation of the results more difficult. Moreover, the score function reported in the right part of Figure 9 shows that, in the clock-unrelated case, there is no significant gain when moving from fingerprints with two features to vectors with three elements.
The receiver classes represented in the left part of Figure 9 show that the one manufacturer’s receivers of different types have similar features. The overlapping between classes observed in Figure 9a compromises the overall score that does not increase even when an additional feature is included for fingerprinting. However, the results observed suggest that clock-unrelated features may allow for the identification of different receiver manufacturers. When considering receivers from the other manufacturer, the Allan Deviation at one second progressively decreases as a function of the receiver generation. This result reflects the fact that more recent receiver models have better Allan Deviations than older models.
Conclusion
This working paper provides initial results towards the fingerprinting of GNSS devices. The PVT solutions provided by GNSS receivers were considered as possible sources of features for fingerprints. It was shown that Doppler-derived time series, i.e., the three velocity components and the receiver clock drift, are more stable to environmental changes and thus should be preferred for receiver fingerprinting. Moreover, clock-related features, i.e., metrics derived from the receiver clock bias and drift, better discriminate the different receiver models. In this respect, a vector of three clock-derived features is sufficient to characterize a receiver model. Clock-unrelated features, i.e., based on the velocity time series, do not always allow for the identification of the receiver model. Despite this fact, experimental results indicate that manufacturer identification should at least be possible using clock-unrelated features.
Additional data collections will be performed as future work to confirm the preliminary results discussed here. A classification framework based on the features identified will also be implemented to demonstrate automatic receiver identification.
Additional Resources
[1] Borio, D., Gioia, C., Baldini, G., and Fortuny, J., “GNSS Receiver Fingerprinting for Security- Enhanced Applications,” Proceedings of the 29th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2016), Portland, OR, September 2016
[2] Bregni, S, Synchronization of Digital Telecommunications Networks, Wiley, June 2002
[3] Chandrashekar, G. and Sahin, F., “A Survey on Feature Selection Methods,” Computers & Electrical Engineering, Volume: 40, Issue: 1, 2014.
[4] European Commission, “Regulation (EU) No 165/2014 of the European Parliament and of the Council of 4 February 2014 on Tachographs in Road Transport,” on-line, 2014
[5] Jafarnia-Jahromi, A., Broumandan, A., Nielsen, J., and Lachapelle, G., “GPS Vulnerability to Spoofing Threats and a Review of Anti-Spoofing Techniques,” International Journal of Navigation and Observation, May 2012
[6] Polak, A. C. and Goeckel, D. L., “Wireless Device Identification based on RF Oscillator Imperfections,” IEEE Transactions on Information Forensics and Security, Volume: 10, December 2015
[7] Pujante, A., “Location Authentication, Enabling New Smartphone Apps,” Inside GNSS, Volume: 9, May-June 2014
[8] Xu, Q., Zheng, R., Saad, W., and Han, Z., “Device Fingerprinting in Wireless Networks: Challenges and Opportunities,” IEEE Communications Surveys and Tutorials, Volume: 18, First Quarter 2016
