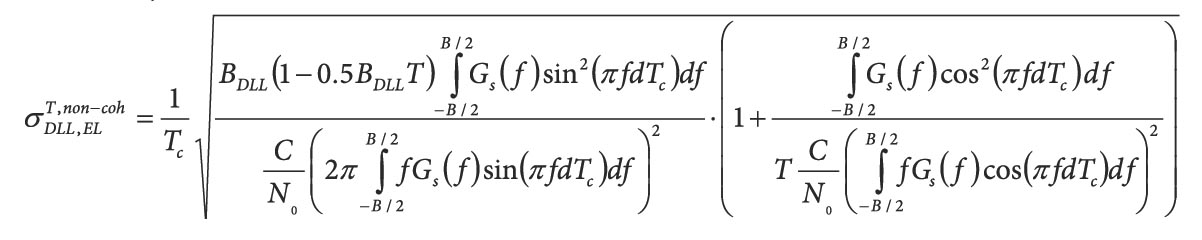 Equations
EquationsWorking Papers explore the technical and scientific themes that underpin GNSS programs and applications. This regular column is coordinated by Prof. Dr.-Ing. Günter Hein, head of Europe’s Galileo Operations and Evolution.
Working Papers explore the technical and scientific themes that underpin GNSS programs and applications. This regular column is coordinated by Prof. Dr.-Ing. Günter Hein, head of Europe’s Galileo Operations and Evolution.
The Galileo Public Regulated Service (PRS) broadcasts as a pair of signals on two frequencies, namely E1 (1575.42 MHz) and E6 (1278.75 MHz). The service is restricted to authorized users by means of spreading code encryption – only receivers equipped with the necessary keys can generate the pseudorandom spreading codes used to modulate the signals. This is similar, in principle, to the GPS P-code signal, which is also an encrypted signal broadcast on two frequencies.
Over the last number of decades civilian users, motivated by the need to exploit the dual frequency nature of the GPS P-code to compensate for ionospheric delay, have developed a number of techniques to process the P-code without requiring access to the encryption keys. These techniques include codeless, semi-codeless, and cross-correlation techniques. This naturally leads to the question as to whether similar approaches might work for the PRS.
There are, however, a number of significant differences between the two cases. First, the PRS signals on E1 and E6 are quite different from each other, with different bandwidths, modulations, and chipping rates. This precludes the use of a cross-correlation approach. Next, quite early in the history of GPS it was noticed by the civilian community that the P-code is encrypted by a stream cipher spreading sequence (the so-called W-code) that has a lower rate than the P-code.
This enables receivers to take advantage of their knowledge of the P-code chips over the duration of each W-code chip to perform fully coherent processing. The resulting approach is referred to as semi-codeless processing, as the receiver has knowledge of the P-code, but not the W-code that modulates it. Again, this is not possible for the case of the PRS as no such structure exists, to the best of our knowledge.
Nevertheless, there are a number of reasons why we might wish to extract measurements from the PRS, in particular the E1 PRS signal. For example, codeless processing of the PRS was first proposed in the context of signal quality monitoring (see D. Borio et alia (2012) in Additional Resources). One of the most attractive features of the E1 PRS in particular is its extremely wide bandwidth, which is due to the high rate BOCc (15, 2.5) subcarrier that modulates it. This subcarrier signal has a number of very interesting properties, including a very narrow correlation function, which results in excellent ranging performance in both thermal noise and multipath fading channels. However, the correlation function is multi-peaked, which leads to difficulties in tracking due to the possibility of tracking a correlator side-peak.
A second use of codeless PRS processing is in anti-spoofing systems such as that proposed by a group of researchers at Stanford University (see S. Lo et alia in Additional Resources). The signals received by a mobile, potentially spoofed unit can be cross-checked against those received at a reference and presumably unspoofed station. The reliability and accuracy of this cross-check is a function of the accuracy with which the signal can be measured and the integrity of the signal itself, both of which can be enhanced with improved signal processing techniques, such as those explored here.
One issue that can affect high order BOC signals, such as the E1 PRS, is the so-called code/subcarrier divergence effect. Due to the wideband nature of the signal it is possible for the code and subcarrier to experience differential delays as they propagate from the transmitter to the receiver. Recent studies have shown that this is primarily due to group delay variation in the receiver front-end, but may also be caused by antenna phase center variation and multipath.
This motivates the need to be able to measure the code/subcarrier divergence as seen in the field. However, the operational security requirements on the use of the PRS make the deployment of a network of monitoring stations very expensive, and places severe limitations on where the stations can be placed. By removing the need to carry the spreading code encryption keys, the cost per station can be reduced by orders of magnitude.
Such a network may be of benefit to system operators, but other uses can also be imagined: for example, such a network could form part of a civil, or private, authentication system. Thus, we can envisage a low cost monitoring approach, but to do so requires measurements of both code and subcarrier phase from the E1 PRS, without having access to the spreading codes. Unfortunately, codeless processing only allows for measurements of the subcarrier phase. To this end we introduce the concept of “Codeless Code Processing” – a simple extension of codeless processing for BOC signals that provides code phase measurements in addition to subcarrier phase measurements.
Signal Models
We model the signal at the input to receiver signal processing as being the sum of different signal components from different satellites:
Equation (1) (See inset photo, above right, for all equations)
where the sum in m is over all the satellite signals in view, Pm is the total signal power from SV m, fRf is the carrier frequency, ϕ0,m is the initial phase, tmTx(t) is the transmit time of the signals from SV m at receiver time t, and xm(t) is the composite set of signals transmitted by SV m.
The signal xm(t) consists of one or more components with a fixed amplitude and phase relationship (though this may be modified by the channel between the transmitter and the receiver):
Equation (2)
where Aml is the amplitude of the lth component, ϕml is its relative phase, gml(t) is the chip sequence, including data bits, secondary code, and primary spreading sequence, and sml(t) is the periodic subcarrier. As an example, consider the Galileo E1 signal, which has three components: the PRS, E1B, and E1C. The E1B and E1C components are in-phase with the carrier, while the PRS is 90° out of phase. This means that we can use the carrier tracking from the OS to aid in our PRS processing.
For the E1 PRS, the subcarrier goes through six complete cycles in each chip. This is illustrated in the blue (unfiltered) plot in Figure 1. The transmitted signal consists of an infinite train of these pulses, modulated by +/– 1 valued chips. These chips are unknown to unauthorized users and so appear as a random sequence.
Codeless Processing
The high rate of the subcarrier with respect to the code can be used to advantage in codeless processing in which the subcarrier is wiped-off from the received signal and the result is coherently integrated over each individual chip. The results are then squared, which serves to remove the chip values and doubles the carrier phase, and integrated. The squaring process naturally leads to a significant loss in SNR, which must be overcome by integrating over prolonged periods of time (on the order of hundreds of milliseconds to seconds). The codeless correlator output is computed as:
Equation (3)
where K is the number of chips over which the correlation is computed and nk is the index of the first sample in the kth chip. The correlation in the square brackets is computed over each individual chip, then the result is squared and summed over K successive chips. Note that this squaring is a complex operation, in that it retains both real and imaginary components of the input. This is in contrast to the square magnitude operation, which always generates a real output.
Very long integration times are possible due to the coherent relationship between the signal components from any one satellite, since the vast majority of the signal dynamics can be removed by aiding with the Doppler estimates from the OS tracking loop. However, tracking quantities with loop update rates on the order of seconds requires careful construction of the parameter estimators. In this work we limit the total integration time to no more than 400 milliseconds, which provides good output SNR for C/N0 down to about 40 dB-Hz.
The squaring operation completely removes the multi-access protection provided by the spreading codes. We rely on frequency domain separation, in the form of Doppler differences, to provide multi-access protection from other satellites, and phase and/or subcarrier orthogonality to avoid self-interference from other signals in the same frequency band on the same satellite.
Note that in (3), the start of each chip integration is assumed to be perfectly aligned with the subcarrier. This permits us to estimate the subcarrier phase, by maximizing the correlator output, but does not provide a mechanism for generating separate code phase estimates.
Extension to Code Tracking
Here we extend the codeless correlation concept, by allowing the integration over each chip, the summation over n in (3), to slide with respect to the subcarrier. This is equivalent to allowing for a divergence between the code and subcarrier in the local replica, to match the potential divergence in the received signal.
One significant advantage of this approach is that it allows us to take a measurement on the PRS with an ambiguity of one chip (about 120 meters) rather than an ambiguity of one half of a subcarrier cycle (about 10 meters).
The extension of the codeless concept to code tracking involves generalizing (3) to account for the code delay τc as follows:
Equation (4)
where: τ̂c is the receiver estimate of the PRS code phase, nk(τ̂c) is the receiver’s estimate of the index of the first sample in the kth chip given the code phase estimate, and
Nk(τ̂c) = nk+1(τ̂c) − nk(τ̂c)
is the receiver’s estimate of the number of samples in the kth chip.
Note that there is very little difference between (3) and (4), only that the local code replica is effectively allowed to slide with respect to the local subcarrier replica.
Assuming that the receiver front-end bandwidth is less than 90 megahertz, O’Driscoll and Curran (see Additional Resources) show that the correlation function is approximately given by:
Equation (5)
Equation (6)
Equation (7)
Equation (8)
and δϕk is the average phase error over the kth chip. This correlation function is sensitive to the code phase error with an ambiguity of one chip and to the subcarrier error with an ambiguity of one half cycle. Figure 2 shows this correlation function evaluated on a PRS signal that has been passed through an eighth order Butterworth filter with a two-sided bandwidth of 50 megahertz, assuming unit power and perfect phase tracking.
For signals from other satellites with the same subcarrier modulation, the only source of multi-access protection in codeless processing derives from the relative Doppler, both through the sliding of the code phase error over the correlation interval, and the carrier Doppler through the summation term in (5), which results in the familiar sinc roll-off with frequency for a constant Doppler offset between local replica and incoming signal. When two satellites have the same Doppler as seen by the receiver, then a “Doppler collision” will result, leading to a significant multi-access noise contribution, as will be demonstrated in the results section.
Design of the Codeless Code Tracking Loop
Given that we have a codeless correlation function sensitive to both code and subcarrier tracking errors, it is now necessary to design a tracking loop to drive those errors to zero. To do so requires discriminator functions, one each for the code and subcarrier tracking that can detect the associated error.
Defining Early (E) and late (L) correlator outputs as
Equation (9)
Equation (10)
Equation (11)
Then we can construct the Early Minus Late Power (EMLP) discriminator as follows:
Equation (12)
Note that this definition of the E and L correlators assumes that the offset between the local replica code and subcarrier delays is the same in all correlators. This assumption differentiates this approach from the Double Estimator (DE) approach, and is referred to as the Very Early Minus Late (VEML) approach (see Additional Resources).
We now consider two correlator spacings which enable us to generate separate discriminators for the subcarrier and code phase tracking errors as shown in Table 1.
Codeless Tracking
A mechanism for computing the codeless code correlation function at a variety of code and subcarrier phase estimates is shown in Figure 3. This structure is referred to as the Very Early Minus Late (VEML) structure, as it computes five correlator outputs:
1. Very Early (VE): the signal is correlated with very early replicas of both the code and subcarrier (used for code tracking)
2. Early (E): the signal is correlated with an early replica of both code and subcarrier (used for subcarrier tracking)
3. Prompt (P): the signal is correlated with the current best estimate of the code and subcarrier (used for phase tracking and C/N0 estimation).
4. Late (L): the signal is correlated with late replicas of both the code and the subcarrier (used for subcarrier tracking)
5. Very Late (VL): the signal is correlated with very late replicas of both the code and the subcarrier (used for code tracking).
Note that the signal dynamics are tracked in the OS tracking loops, which provide carrier aiding to the codeless loop as described in more detail by D. Borio et alia (2013).
Once subcarrier lock is achieved, the receiver then begins to use the VE and VL correlators to drive εc to zero. This involves a tracking loop to drive the “code NCO.” By aiding the code tracking loop with the subcarrier, this code tracking loop need only track the residual dynamics of the code/subcarrier divergence (again, see Additional Resources). In general we expect this divergence to be an extremely narrowband dynamic process, and so we can use very low loop bandwidths, on the order of hundredths to tenths of hertz. This is illustrated in Figure 4.
The above receiver structure has been implemented in the open source GNSS-SDR software defined radio receiver (see C. Fernandez-Prades et alia, Additional Resources). In the following section we demonstrate the operation of this receiver structure using both simulated and live signals.
Results
To demonstrate the utility of the approach, two different data sets were collected. The first was collected from a hardware simulator, which uses a known pseudorandom binary sequence on the E1 PRS. This provides us with a mechanism for directly comparing fully coherent processing with the codeless approach, albeit with simulated data. The second data set is a longer data set recorded in a static open sky environment with two Galileo satellites in view. This second data set demonstrates the codeless code processing approach with real signals, albeit without the ability to compare the results with full coherent processing, due to our ignorance of the broadcast PRS spreading codes.
Simulator
The simulated data set was collected on a hardware simulator that generates a “pseudo-noise” signal in the form of a down-sampled version of the P-Code (see Manufacturers). The simulation scenario was a short (40-second) dynamic scenario with six Galileo satellites in view. The C/N0 was high (on the order of 50 dB-Hz) for all signals. The maximum speed was 100 kilometers per hour.
The data were recorded with a wideband digitizer, which collected the data with a sampling rate of 62.5 mega samples per second complex baseband sampling, giving a two sided bandwidth of approximately 50 megahertz. The data were recorded as 16 bit complex interleaved I, Q pairs.
The software receiver was configured with the codeless tracking parameters given in Table 2. Note the divergence bandwidth, which is particularly small.
The data were processed both codelessly and using the PN codes used by the simulator to generate the signal. Pseudorange measurements were generated for both processing techniques based on the code delay estimates, with the codeless measurements being made modulo one code chip, or approximately 120 meters.
Figure 5 shows the absolute value of the codeless correlator outputs, normalized for presentation. It is clear from the figure that the signal is being tracked, with a high signal to noise ratio. As described in the caption, a number of interesting observations can be made from this figure.
First, the early (E) and late (L) correlators, which track the subcarrier phase, pull in very rapidly, within a couple of seconds. This demonstrates that: a) there was an initial subcarrier phase estimation error when the codeless PRS tracking began; and, b) the codeless tracking loop was able to sense this error and drive it to zero. The second interesting point to note is that the very early (VE) and very late (VL) correlators have a significant initial offset, which remains more or less constant for the first few seconds. After this point, they converge together, finally meeting around the 12-second mark. This is due to the tracking logic in the receiver. First the subcarrier is tracked, and only once subcarrier lock is detected is code tracking enabled. Finally, when code lock is detected, then the correlator spacing is narrowed to improve tracking performance.
This narrowing of the correlator spacing is seen in the tandem jump in the VE and VL correlators at about 12 seconds. The final interesting point to note about the figure is the sudden dip in amplitude across all correlators at about 18 seconds. This, it turns out, is due to a Doppler collision with PRN 12. As discussed above, one of the side effects of codeless processing is the complete removal of the code division multiple access protection afforded by the spreading codes. When two signals have the same Doppler as seen by the receiver, they become indistinguishable without this multiple access protection. Just such a collision occurs between PRNs 2 and 12 in this data set at about the 18-second mark, as shown in Figure 6.
This all seems to suggest that we can indeed extract both code and subcarrier phase measurements from the PRS using only codeless processing. This is confirmed in Figure 7, which shows the difference in code phase and subcarrier phase measurements between the fully coherent (coded) and codeless processing strategies. Note that these differences are taken modulo one chip, or 120 meters for the code phase and modulo one half subcarrier cycle, or 10 meters for the subcarrier phase.
Note from the figure that, after an initial pull-in time of approximately 10 seconds, the code measurements on all satellites align almost perfectly between the coded and codeless processing approaches. Closer inspection shows that there is in fact a small bias of approximately one half meter between the two approaches. These results do give confidence however that the codeless code tracking approach is indeed able to generate accurate code measurements. There does not appear to be any subcarrier phase bias between the coded and codeless processing techniques.
An advantage of the codeless code tracking approach proposed is that it allows us to monitor the divergence between the code and the subcarrier. This is illustrated in Figure 8, which shows the divergence as estimated by both coded and codeless processing techniques. Once again, the approximately one half meter bias between the coded and codeless techniques is apparent, otherwise, however, the codeless approach does appear to give good estimates of the code/subcarrier divergence.
It is interesting to note that for this particular configuration of signal generator and receiver front-end, there is a clear bias of just under three meters (modulo one half the subcarrier cycle) between the code and subcarrier.
While the use of the data from the hardware simulator is very useful in proving the concept of codelessly tracking the code, it is still an idealized situation, with high C/N0, and no receiver antenna in the loop.
Live Galileo Data
To further validate the results presented in the previous sections, a live dataset was collected, which contained signals broadcast from two Galileo satellites. A 30 minute data-set was collected at 1-bit resolution using a sample-rate of 60 megahertz, complex, with a low phase noise, ovenized crystal oscillator used as a reference frequency. The antenna used (See Manufacturers) was permanently installed on a roof with a clear view of the sky down to an elevation of approximately five degrees. The recording was made between 05:10 and 05:40 on December 12, 2015, at the Joint Research Center in Ispra, Italy, located at approximately 45° 48’ 40” North and 8° 37’ 50” East. The C/N0 as measured on the OS signal was on the order of 40-45 dB-Hz, which is up to 10 dB lower than those in the simulated data set.
The tracking configuration differed slightly from that used for the simulated data due to the much reduced C/N0. The parameters are recorded in Table 3. Note that the accumulation time was increased to 400 milliseconds, or 100 code periods to overcome the reduction in C/N0 relative to the simulated data set. The divergence bandwidth was also reduced to 0.01 hertz. This is extremely narrowband, but the effect is visible in this data set due to the fact that the duration is approximately 30 minutes.
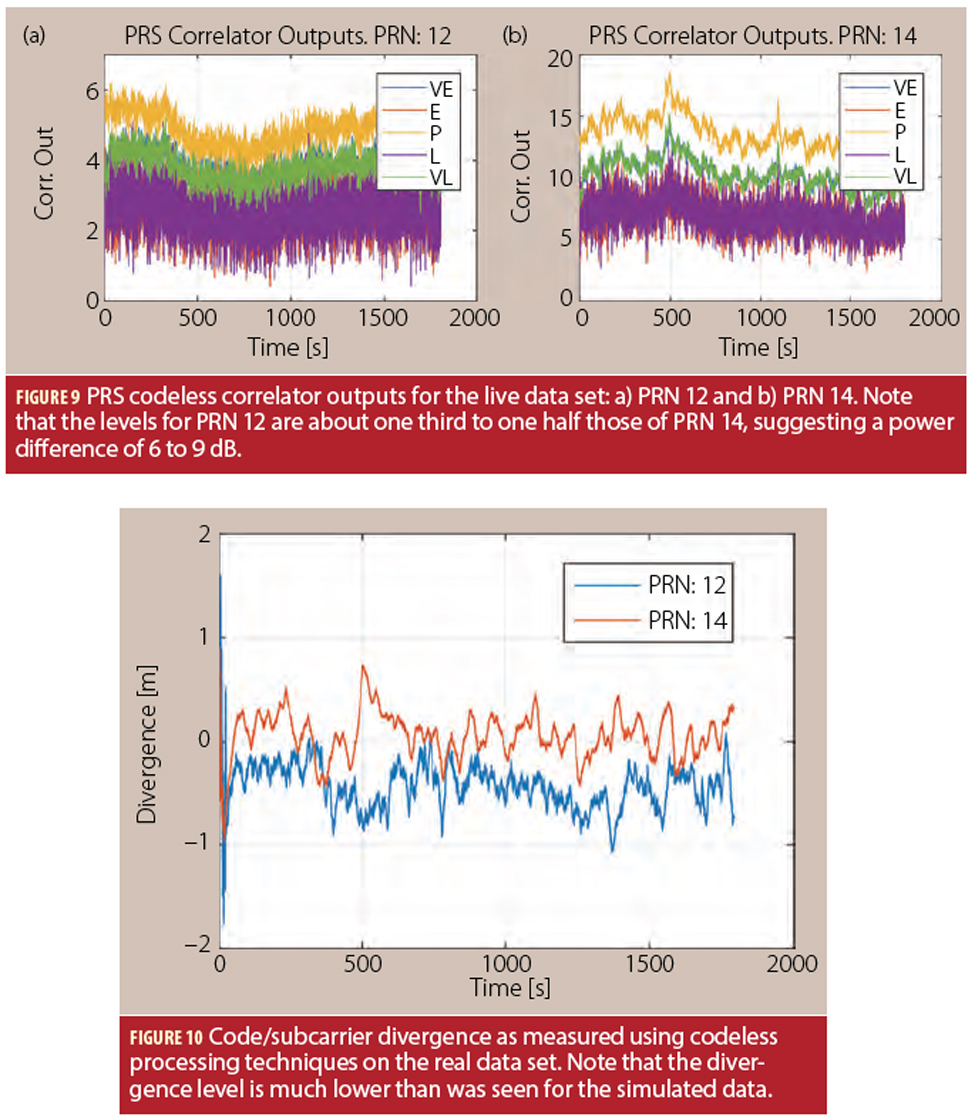
The codeless correlator outputs for the two PRNs in view are shown in Figure 9. Comparing this with Figure 5, we see that the C/N0 is much lower in this case. However, it is clear that the code is being tracked in both plots (the VE and VL correlators are balanced).
This allows us to estimate the code/subcarrier divergence, as was done for the simulated data. Recall, from the simulated data a divergence of approximately three meters was observed. The divergence in this case is shown in Figure 10, and is seen to be less than one meter for both PRNs. Interestingly the divergence for PRN 14 appears to be approximately zero meters, while there appears to be a noticeable bias of about one half meter for PRN 12. While more investigation would be required to determine the exact cause of this difference, it is interesting to note that PRN 12 is an IOV satellite, while PRN 14 is an FOC satellite, which has a significantly different design.
What is clear, however, is that the proposed approach is a viable method for observing temporal variations in the code/subcarrier delay, which may be useful in a signal quality monitoring context.
Conclusion
The motivation for this work arose from a desire to investigate code/subcarrier divergence in high order BOC signals. This phenomenon, whereby non-linear phase effects lead to a relative delay between the code and the subcarrier, can cause severe tracking problems, including frequent subcarrier cycle slips and even loss of lock. The Galileo E1 PRS signal is the largest bandwidth high order BOC signal currently being broadcast, and so is a perfect candidate for the study of code/subcarrier divergence. Unfortunately, the PRS signal is encrypted and subject to a high-level security classification, so obtaining the required information is challenging, to say the least. Through the development of the “codeless code tracking” approach we are able to obtain the required code and subcarrier phase measurements with relatively low cost equipment and without requiring any security infrastructure. A network of receivers implementing this approach could be a means to provide a cheap PRS signal quality monitoring service, or may form the basis of a high-accuracy PRS-based anti-spoofing mechanism.
Future work will investigate the utility of this approach in generating range measurements under multipath conditions, where the wide bandwidth of the PRS signal may provide some added value in reducing measurement noise, even with the reduced signal to noise ratio due to squaring.
Additional Resources
[1] Borio, D., “Squaring and Cross-Correlation Codeless Tracking: Analysis and Generalisation,” IET Radar, Sonar & Navigation, Vol. 5, December 2011
[2] Borio, D., M. Rao, and C. O’Driscoll, “Quality Monitoring of BOC Signals through Codeless Techniques,” Proceedings of the European Navigation Conference (ENC 2012), Gdansk, Poland, April 2012
[3] Borio, D., M. Rao, and C. O’Driscoll, “Codeless Processing of Binary Offset Carrier Modulated Signals,” IET Radar, Sonar & Navigation, Vol. 7, No. 2, 2013
[4] Dunn, C. E., D. C. Jefferson, S. M. Lichten, J. B. Thomas, Y. Vigue, and L. E. Young, “Time and Position Accuracy using Codeless GPS,” Proceedings of the 25th Precise Time and Time Interval (PTTI) Conference, Marina del Rey, CA, December 1993
[5] Fernandez–Prades, C., J. Arribas, P. Closas, C. Aviles, and L. Esteve, “GNSS-SDR: An Open Source Tool for Researchers and Developers,” Proceedings of the ION GNSS 2011 Conference, Portland, OR, September 2011
[6] Lo, S., D. De Lorenzo, and P. Enge, “Signal Authentication: A Secure Civil GNSS for Today,” Inside GNSS, September/October 2009
[7] O’Driscoll, C. and J. T. Curran, “Codeless Code Tracking of BOC Signals,” Proceedings of ION GNSS+ 2016, Portland, OR, September 2016
[8] O’Driscoll, C., J.-A. Avila-Rodriguez, and R. Ioannides, “Bandlimiting and Dispersive Effects on High Order BOC Signals,” Proceedings of ION GNSS+ 2016, Portland, OR, September 2016
[9] O’Driscoll, C., J.-A. Avila-Rodriguez, and R. Ioannides, “Subcarrier Aided Code Tracking of High Order BOC Signals,” Proceedings of ION GNSS+ 2016, Portland, OR, September 2016