In recent years, researchers have explored possible new allocations for Radio Determination Satellite Service (RDSS) and Radio Navigation Satellite Service (RNSS) spectrum from a regulatory point of view. These studies have mainly discussed S-band and C-band in addition to L-band.
The International Telecommunications Union (ITU) Radio Regulations define RNSS as a subset of RDSS. Although the allocations are differentiated — RDSS usually has a paired uplink — both can actually be used for satellite navigation.
In recent years, researchers have explored possible new allocations for Radio Determination Satellite Service (RDSS) and Radio Navigation Satellite Service (RNSS) spectrum from a regulatory point of view. These studies have mainly discussed S-band and C-band in addition to L-band.
The International Telecommunications Union (ITU) Radio Regulations define RNSS as a subset of RDSS. Although the allocations are differentiated — RDSS usually has a paired uplink — both can actually be used for satellite navigation.
The eventual need of GNSS systems for additional frequency resources or signals in S-band and/or C-band is not driven by the desire to improve the pseudoranging or timing performance, but primarily to introduce alternative and complementary capabilities to those services already offered by systems now in operation or under development.
In fact, GNSS pseudoranging or timing performance could be improved with availability of new code division multiple access (CDMA) signals in the upper L-band alone. These could be defined in the so-called E1+G1 band, for example, where some room is still available if compatibility with the adjacent radio astronomy band and GLONASS could be achieved.
In any case, any signal occupying the whole E1/G1 band would have to be backward-compatible and symmetrical in spectrum and correlation characteristics to avoid creating pseudoranging bias. Furthermore, having a very wide band signal in the lower and upper L-bands would potentially allow significant improvement in terms of pseudoranging performance thanks to the very accurate dual-frequency, wideband ionospheric correction and raw pseudoranges that would be available.
In fact, this is the only way for any new signal to significantly improve the pseudoranging performance, because C-band today is only 20 MHz wide (5010–5030 MHz) and S-band is restricted to 16.5 MHz (2491.75 MHz ±8.25 MHz.
“Note that an alternate binary offset carrier with CBOC on each side — that we could define as AltBOC(15, CBOC), for example — or an equivalent signal filtered in the E1/G1 band could by itself prove superior in terms of accuracy compared to the current multiplexed BOC (MBOC) planned for Galileo E1 and GPS L1, while still preserving the necessary backward compatibility with a composite BOC (CBOC) in E1.
In principle, another very important field for improving accuracy worldwide without the need of extra frequency bands (that is, in addition to L-band) is a technique called integer ambiguity resolution on undifferenced phase (IARUP) or possible equivalent techniques, which will allow very precise positioning accuracies close to a few centimeters in real time (Figure 1, see inset, above).
IARUP is described further in the paper by D. Laurichesse and F. Mercier listed in the Additional Resources section at the end of this article. (We should point out that such techniques are also known by the acronym PPP-Wizard, standing for “Precise Point Positioning With Integer Zero-difference Ambiguity Resolution Demonstration.”)
Having this in mind and recalling that our objective is to focus on S-band, alternative solutions that employ C-band and/or G1/G2. L-band will not be discussed further in this article, except for the relevant L/S-band link budget comparisons.
Regarding C-band, several studies have been undertaken in recent years to investigate the suitability of this frequency band for GNSS purposes and possible alternatives for a signal baseline, mainly in the framework of the European Space Agency’s GNSS Evolution Program. (The interested reader can refer to the papers by J. A. Avila-Rodriguez et alia (2008b) and A. Schmitz-Peiffer et alia listed in Additional Resources.)
This two-part column will show that potential new services in S-band are technically feasible, from the perspectives of link budget and radio frequency compatibility. We must also underline the fact that the results presented in this column neither pretend to cover the whole palette of GNSS signals and frequency resources that could be discussed, nor pretend to be an official baseline for an evolved Galileo system.
Future developments could be in different or complementary directions to those that we will discuss here. Having said this, we recall that the main objective of the authors is to open a constructive discussion on where GNSS could evolve to. The first part of this column will take up the issues of S-band’s potential for GNSS operations, presenting results of several comparative technical analyses.
Part 2, which will follow in the October issue of Inside GNSS, will focus on the subject of compatibility and interoperability with other systems operating at S-band as well as signal modulations that might work well for GNSS services there.
Potential Benefits of S-band for Navigation
New functions and services that could be imagined for potential S-band signals do not necessarily include the improvement of the ionospheric correction. In fact, a new signal in the G1 L-band would also significantly improve the ionospheric correction efficiency as discussed above.
Moreover, Globalstar, a low Earth orbit (LEO) mobile telecommunication constellation, also applies S-band Doppler compensation based on radio links between the ground and the LEO satellites in addition to its GPS on-board real-time orbit determination and synchronization. Further, the new functions and services provided by S-band are rather tighter hybridizations between mobile communication services and navigation services.
The list of imaginable applications based on the combined use of S- and L-band or S-band alone is a lengthy one, including the following:
- An accurate self-positioning of future Globalstar mobile phones using Galileo, without the need to add any L-band hardware in the Globalstar (or other mobile com) terminal to save costs in this equipment. Single-frequency S-band ionospheric correction could be provided using techniques such as those described in other research on this topic listed in the Additional References.
- Assistance of GNSS acquisition indoor using Globalstar signals, or using other mobile communication signals also transmitted in S-band
- To perform the orbit and time determination of both Galileo (or another GNSS system) and Globalstar satellites, thanks to a single ground network of updated Galileo Sensor Station (receivers), using double difference measurements in S-band, single frequency ionospheric determination in S-band, and intersystem assistance/cross-validations thanks to L-band measurements. A GNSS system could then offer the time and orbit determination of Globalstar and/or other mobile satellite service (MSS) systems, if the necessary related security measures were taken.
- To assist the acquisition of MSS signals like the Globalstar ones, providing an accurate time, without requiring any L-band–specific hardware in the mobile com terminal.
- To use the communication channel to provide assisted-GNSS to a GNSS-embedded receiver. This would allow communication to support GNSS. A possible approach could be, for instance, to use the Open Mobile Alliance–Secure User Plane Location (OMA-SUPL) approach.
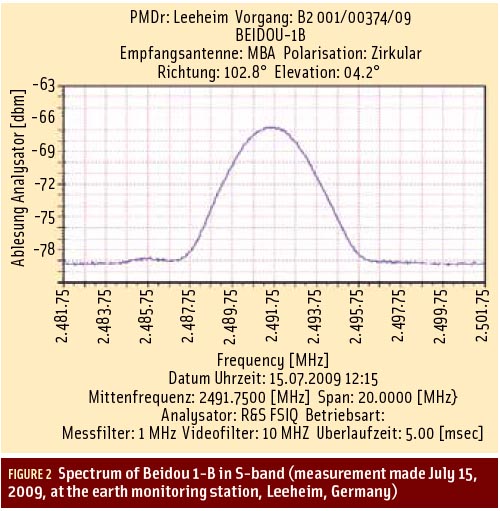
- To allow RDSS multi-constellation positioning in S-band by means of Beidou/Compass future S-band signals or from the Indian IRNSS/GINS, which is also planned to transmit at 2491 MHz. An example of the signal that could be employed is shown in Figure 2, which depicts the Chinese geostationary orbit satellite (GSO) RDSS signal at 2491 MHz. The paper by T. Grelier et alia (2006) cited in Additional Resources has measured and analyzed the Beidou GNSS S-band pseudonoise (PN) code spectrum lines.As we can see, this is the same central frequency employed by Globalstar. We also noticed that the Japanese high accuracy clock (HAC) GNSS signal experiment already uses a 1023 chips — 1.023 Mcps code at 2491 MHz transmitted from the ETS VIII geostationary satellite of JAXA. Current modernized GPS satellites are also provided with an experimental search and rescue (SAR) payload transmitting in S-band.
- We should also note that with equivalent signal bandwidths, L+S ionospheric dual-frequency corrections are more accurate than L+L ones. This advantage remains for dual-frequency classical ionospheric corrections without the need to require wider bandwidths. However, this benefit does not appear for single-frequency ionospheric corrections where the higher the carrier frequency, the smaller the ionospheric delay is, but also the smaller the code-carrier divergence that results.On the other hand, because this code-carrier slipping also allows single-frequency retrieval of the ionospheric delay, the efficiency of ionospheric correction using combined classical dual-frequency and single-frequency correcting techniques is approximately the same no matter what the the central carrier frequencies are. (See the discussion in the papers by J.-L. Issler et alia and O. Julien et alia in Additional Resources.)The only noticeable advantage of S-band (or C-band) related to ionospheric corrections is smaller scintillations compared to L-band.
- To allow RNSS multi-constellation positioning and inter-system assistance in S- and L-band, thanks to the previously mentioned Asian, U.S., and European systems.
All these applications might be satisfied by a single signal, hosting several services simultaneously. Up till now, no need for two different Galileo waveforms and spectrum in S-band has been identified. However, this does not mean that an eventual Galileo S-band signal should necessarily have only one main lobe.
It is worth noting that L/S-band frequency was selected for low-cost radio development (commercial wireless technology) in a GPS IIF SAR low-cost design study involving a 2.4 GHz downlink. S-band is also used for satellite formation flying RF GNSS technology, using GPS-like C/A codes. The potential services to be provided by Galileo in a hypothetical future S-band system are still under study.
Link Budget
We have calculated a link budget to quantify the effect of an S-band signal upon a satellite’s power supply. For the sake of the comparison between signals in L-band and the potential signal in S-band, we assumed that the new signal will guarantee at least the same received power on the ground and offer the same performance in terms of pseudorange accuracy, as the Galileo Open Service in E1/L1.
The Galileo OS Signal-in-Space Interface Control Document (ICD) sets a minimum received power of -157.25 dBW for its open service on E1 at an elevation angle of five degrees. Table 1 shows that an effective isotropic radiated power (EIRP) of 33.7 dBW would need to be transmitted in S-band to obtain the same power on the ground, which represents an increase of four decibels from what is required in E1. This is needed in order to compensate for the higher free-space losses in S-band.
In order to assess pseudorange accuracy, the signal modulation has to be taken into account. We considered five different possible alternatives:
- Bi-phase shift key, BPSK(1) — “Globalstar like” or “IRNSS like” signal, occupying only the central portion of the available spectrum
- BPSK(4) — analog of the signal transmitted by the Beidou-1 geostationary satellites
- BPSK(8) — the idea behind this signal would be to effectively occupy the whole S-band RDSS spectrum;
- BOC(1,1) — having the same spectrum as the core of the GPS/Galileo CBOC at E1 central frequency, this signal could ensure high communality;
- CBOC(6,1,1/11) — to use the same modulation already fixed to be the Galileo OS signal in the E1/L1 band would guarantee maximum communality within the S-Band signal and the Galileo OS and GPS civil signals.
In the second part of this column to be found in the October Issue of Inside GNSS, we explore the use of orthogonal frequency division multiplex (OFDM) modulation.
For each of the modulations considered here, we have calculated the power that is required to be transmitted to obtain the same raw thermal noise pseudorange error as that of E1 OS.
In order to calculate the minimum required carrier-to-noise density ratio (C/N0) for a given thermal noise value, we followed the same approach as that described in the paper by M. Paonni et alia cited in Additional Resources, where the code tracking error is calculated with the theory presented in the referenced article by J. Betz.
The steady state code tracking error expressed in terms of the standard deviation of the thermal noise jitter σDLLt [chips] adopts the following form for the particular case of a non-coherent early-late discriminator:
where Tc is the chip period, BDLL is the delay-locked loop (DLL) bandwidth, B is the double-sided RF front-end bandwidth, T is the coherent integration time, C/N0 is the carrier-to-noise density ratio, and Gs(f) is the power spectral density of the signal.
We begin by calculating the thermal noise for the Galileo E1 OS signal. To do this, a value of signal-to-noise ratio is needed, which we obtained using the link budget presented in Table 2. In this link budget a receiver antenna gain of -3 decibels and implementation losses of 2 decibels have been considered.
As can be read in the table, a C/N0 of 39.25 dBHz has been obtained. Using this value, the pseudorange error has been also calculated using the previously introduced expression. Considering a coherent integration time of four milliseconds, a loop bandwidth of one hertz, a 12.27 megahertz front-end bandwidth and a 0.1-chip spacing, this calculation produces a code noise of 0.25 meter.
The idea that has been used in order to introduce new signals for the S-Band is to fix the minimum transmitted power for each signal so that the ranging performance is always at least equal to that of the Galileo E1 OS. Therefore, the C/N0 required for each of the considered modulations in S-band can be deduced by the value just calculated. In the case of CBOC it will be the same as for E1 (as the pseudorange error does not vary with the carrier frequency), namely 39.25 dBHz.
For the other modulations the C/N0 has been obtained simply by inverting the thermal noise jitter expression. A chip spacing of 0.1 chips and a front-end bandwidth of 16.5 megahertz have been used to produce the results.
Once the C/N0 is determined, the required transmitted power is calculated making a reverse link budget calculation. Table 3 summarizes the obtained results.
Note that Table 3 shows a minimum EIRP for the BPSK(8) signal that is higher than the values calculated to guarantee the minimum required C/N0. This is because a minimum received power on the ground of -157.25 dBW also has to be guaranteed, and this leads to a minimum EIRP of 33.7 dBW.
Therefore, for BPSK(8) modulations the limiting factor for the transmitted power is the received power on the ground, while for BOC(1,1), BPSK(1), and BPSK(4) it is the pseudorange accuracy, which is consistent with the fact that the pseudorange error decreases as the signal bandwidth increases.
Table 4 summarizes the obtained values for the transmitted power, as well as the corresponding maximum power flux density (PFD) level on the ground within the band, which has been calculated through integration of one megahertz of the signal’s power spectral density (PSD) around the maximum of its main lobe.
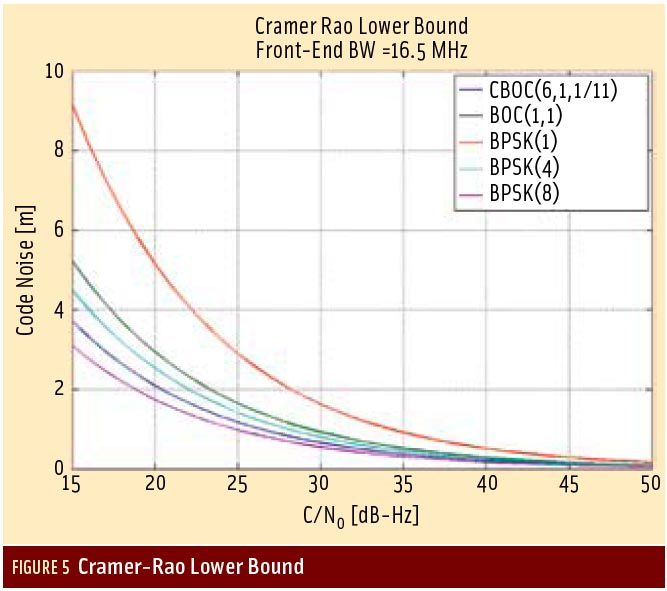
In order to complete the performance comparison between the different modulations under study, we also undertook an analysis of the multipath resistance performance. Multipath error envelopes and their running averages have been assessed for the various signals with the results shown in Figure 3 and Figure 4.
As can be seen in these plots, for short multipath the CBOC modulation outperforms all the other solutions studied here, while BPSK(8) performs best when considering multipath with a longer delay. This result comes as no surprise, because CBOC performs better than the BPSK(4) and even better than the BPSK(8) for short multipath due to its front-end bandwidth of 16.5 megahertz.
The advantage of the higher chip rate of the BPSK(4) and BPSK(8) is more than offset by the quite narrow receiver bandwidth that has been assumed. We can also observe this by plotting the Cramer-Rao Lower Bound for the five signals, as represented in Figure 5.
One would have expected that, given the higher chip rate of the BPSK(4) and BPSK(8) signals , the ranging performance of the CBOC(6,1,1/11) modulation should be much worse. This is not happening because the performances are not analyzed in terms of infinite bandwidth but instead for signals filtered over the available bandwidth. Consequently, the filtering losses that the two BPSK signals are experiencing worsen their ranging performance.
Conclusion and Further Work
This article has considered S-band signal design criteria related to raw pseudorange thermal noise in comparison with L-band and in terms of the C/N0 needed for signal acquisition. Several other signal design criteria would have to be considered in the future, in addition to these. For instance, for a given power flux, wideband signals such as BPSK(8), BPSK(4), and CBOC are more interesting than the other signals considered for indoor applications.
For such a given power flux, the wider the band occupied by the main lobe(s), e.g, for BPSK(8), the higher the received power — and, therefore, the higher the indoor penetration — would be. As a result, wideband modulations that generate small multipath errors for reflections coming from various sides of a building are more interesting to consider for indoor applications.
Another possible signal design criteria is interoperability with open or commercial signals of other systems, such as the planned Indian Regional Navigation Satellite System (IRNSS) and/or Globalstar. These two examples of signal design criteria — efficacy in indoor environments, interoperability with other system(s) — might be met by employing multiple main-lobe signals.
Satisfying all the required signal design criteria would be much complicated if two different GNSS waveform and spectrum, associated to separated services, would have to be fitted in S-band. This difficulty would be compounded by the need to preserve a certain spectral separation with non-interoperable services provided by other GNSS systems in S-band, such a spectral separation being another signal design criterion.
Taking into account all these signal design criteria, and not only the two ones considered in Table 4, a reasonable PFD limit for a GNSS signal in S-band seems to be close to – 126 dBW/MHz/m².
In Part 2 of this column on S-band and GNSS, we will return to the subject of inter-system interference and interoperability, with particular attention on Globalstar. We will also consider the OFDM modulation further as a candidate GNSS signal design element in S-band.
Disclaimer
The authors would like to make it clear that no extra frequency plan has been decided yet in Europe for the second generation of Galileo in addition to the frequency plan backward compatible with the current navigation signals of Galileo. Neither has it been decided yet whether in the future the second generation of Galileo will transmit navigation signals in S-band in addition to L-band. Accordingly, this column should be considered as a scientific exercise that only emphasizes the great interest in considering use of this band for GNSS.
Additional Resources
[1] Antreich, F., and J. A. Nossek, and J-L. Issler, “GNSS Signal Design Considering Receiver Performance,” Navitec ‘08, Noordwijk, December 2008
[2] Avila-Rodriguez, J-A., (2008a) and G. W. Hein, S. Wallner, J-L. Issler, L. Ries, L. Lestarquit, A. de Latour, J. Godet, F. Bastide, T. Pratt, J. Owen, M. Falcone, T. Burger, “The MBOC Modulation: The Final Touch to the Galileo Frequency and Signal Plan,” Proceedings of ION-GNSS 2008, pp. 2189–2198, Fort Worth, Texas USA, September 2008
[3] Avila-Rodriguez, J. A., (2008b) and S. Wallner, J.H. Won and B. Eissfeller, A. Schmitz-Peiffer and J.J. Floch, E. Colzi and J.L. Gerner, “Study on a Potential Galileo Signal and Service Plan for C-Band,” ION-GNSS 2008, Savannah, USA, September 2008
[4] Berthias, J-P., and P. Broca, A. Comps, S. Gratton, D. Laurichesse, and F. Mercier, “Lessons Learned from the Use of a GPS Receiver in Less Than Optimal Conditions,” CNES seminar, Toulouse, France, January 2002
[5] Betz, J. W., “Generalized Theory of Code Tracking with an Early Late Discriminator, Part 1: Lower Bound and Coherent Processing,” IEEE Transactions on Aerospace and Electronic Systems, vol. 45, no. 4, pp. 1538-1550, 2009
[6] Cheung, R. P., and S, Lee, and T. A. Vo, “Feasibility Study of a Low-Cost Search & Rescue Payload Onboard the GPS Satellites,” ION GPS 2000, Salt Lake City, Utah, USA, September 2008
[7] Cohen, C., and B. Pervan, and B. Parkinson, Estimation of Absolute Ionospheric Delay Exclusively through Single-Frequency GPS measurements, ION GPS 1992, Albuquerque, New Mexico, USA, September 1992
[8] Fleury, R., and M. Clemente, P. Lassudrie-Duchesne, and F. Carvalho, “Modelling of High-Order Errors for New Generation GNSS,” Anales des Telecommunications, vol. 64 no. 9-10, pp. 615-623, 2009
[9] Grelier, T. (2006), and L. Ries, J.-L. Issler, New Spectral Measurements of GNSS Signals,” 2006 ION National Technical Meeting, Monterey, California, USA, January 2006
[10] Grelier, T. (2008), and A. Garcia, E. Péragin, L. Lestarquit, J. Harr, D. Seguela, J.-L. Gerner, J.-L. Issler, J.-B. Thevenet, N. Perriault, C. Mehlen, C. Ensenat, N. Wilhelm, A.-M. Badiola Martinez, P. Colmenarejo, “GNSS in Space, Part 1: Formation Flying Radio Frequency Missions, Techniques, and Technology,” Inside GNSS, vol. 3, no. 8, November/December 2008
[11] Grelier, T. (2009), and A. Garcia, E. Péragin, L. Lestarquit, J. Harr, D. Seguela, J.-L. Gerner, J.-L. Issler, J.-B. Thevenet, N. Perriault, C. Mehlen, C. Ensenat, N. Wilhelm, A.-M. Badiola Martinez, P. Colmenarejo, “GNSS in Space, Part 2: Formation, Flying Radio Frequency Missions, Techniques, and Technology,” Inside GNSS, vol. 4, no. 1, January/February 2009
[12] Hein, G. W., and J.-A. Avila-Rodriguez, S. Wallner, B. Eissfeller, M. Irsigler, J-L. Issler, “A Vision on New Frequencies, Signals and Concepts for Future GNSS Systems,” Proceedings of ION-GNSS 2007, pp. 517-534, Fort Worth, Texas, USA, 2007
[13] Inoue, T., and S. Nakamura, R. Nakamura, and S. Katagiri, “ETS-VIII High Accuracy Clock Synchronisation Experiments,” 2F15 ETS-VIII, 2008 Japan Science and Technology Agency conference, 2008
[14] Issler, J.-L., and L. Ries, J-M. Bourgeade, L. Lestarquit, and C. Macabiau, “Probabilistic approach of frequency diversity as interference mitigation Means,” ION GPS 2004, Long Beach, California, USA, September 2004
[15] Julien, O., and C. Macabiau, J.-L. Issler, “Ionospheric Delay Estimation Strategies Using Galileo E5 Signals Only,” ION GNSS 2009, Savannah, Georgia, USA, September 2009
[16] Laurichesse, D., and F. Mercier, “Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP,” Proceedings of ION-GNSS 2007, pp. 839–848, Fort Worth, Texas, 2007
[17] Lestarquit, L., and N. Suard, and J.-L. Issler, “IONO-GPS Software: Determination of the Ionospheric Error Using Only L1 Frequency GPS Receiver,” 1997 ION National Technical Meeting, Santa Monica, California, USA, January 1997
[18] Moreno, R., and N. Suard, and L. Lestarquit, “Ionospheric Delay Using Only L1: Validation and Application to GPS Receiver Calibration and to Inter-frequency Biases AEstimation,” 1999 ION National Technical Meeting, San Diego, California, USA, January 1999
[19] Nakagawa, F., and Y. Takahashi, R. Tabuchi, J. Amagai, S. Tsuchiya, S. Hama, and H. Noda, “Results of Time Comparison Equipment on ETS-VIII. Time transfer experiments,” 2F16 ETS-VIII, Japan Science and Technology Agency conference, 2008
[20] Nisner, P., and M. Trethewey, “GPS Ionosphere Determination Using L1 Only,” 1996 ION National Technical Meeting, Santa Monica, California, USA, January 1996
[21] Paonni, M., and M. Anghileri, J.-A. Ávila-Rodríguez, S. Wallner, and B. Eissfeller, “Methodologies for the Determination of the Minimum Required Carrier to Noise Ratio to Receive GNSS Signals,” 4th European Workshop on GNSS Signals and Signal Processing, Germany, December 2009
[22] Schmitz-Peiffer, A., and L. Stopfkuchen, F. Soualle, J.-J. Floch, R. King, A, Fernandez, R. Jorgensen, B. Eissfeller, J.-A. Avila-Rodriguez, S. Wallner, J.H. Won, T. Pany, M. Anghileri, B. Lankl, T. Schüler, and E. Colzi, “Assessment on the Use of C-Band for GNSS within the European GNSS Evolution Program,” ION-GNSS 2008, Savannah, Georgia USA, September 2008
[23] Thevenon, P., and M. Bousquet, Th. Grelier, L. Ries, D. Roviras, “Regulatory Analysis of Potential Candidate Bands for the Modernisation of GNSS Systems in 2015-2020,” Satellite and Space Communications, pp. 172-175, IEEE International Workshop, 2008
[24] Xia, R., “Determination of Absolute Ionospheric Error Using a Single Frequency GPS Receiver,” ION GPS 1992, Albuquerque, New Mexico, USA, September 1992