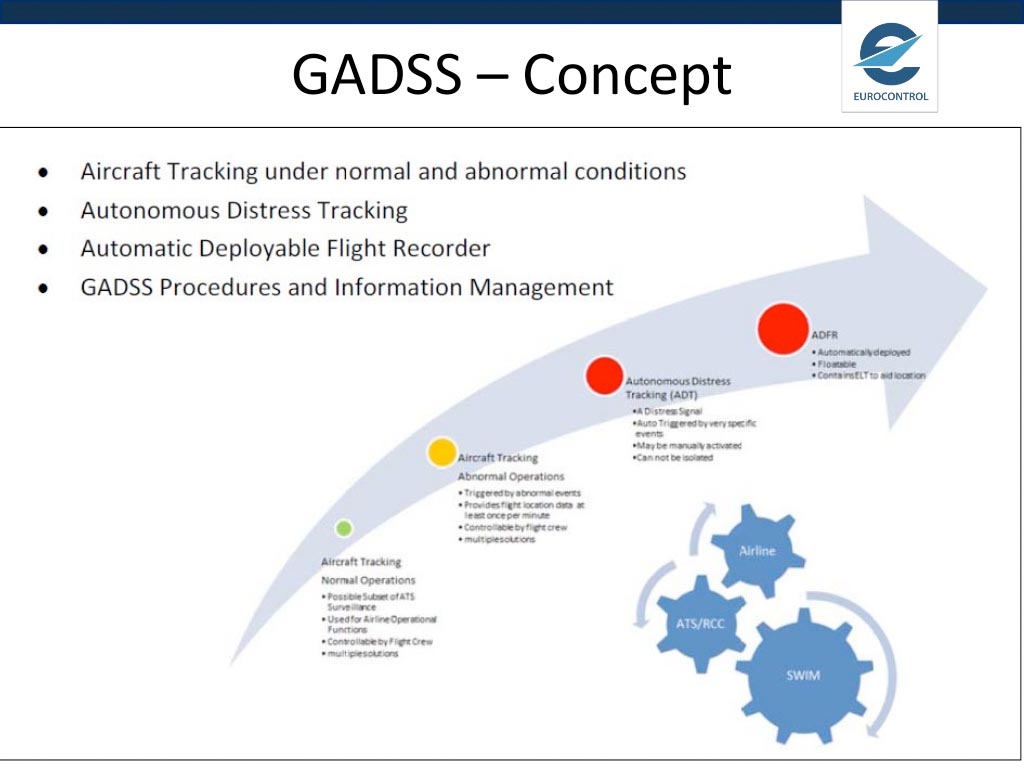
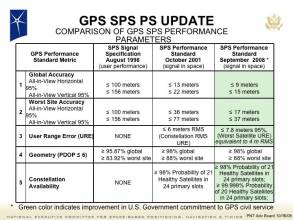
Q: The RTCM has announced a new version of its widely used differential GPS (DGPS) standard. Why did the group decide a new standard — Version 3 — was needed, and what are the benefits compared to Version 2?
Q: The RTCM has announced a new version of its widely used differential GPS (DGPS) standard. Why did the group decide a new standard — Version 3 — was needed, and what are the benefits compared to Version 2?
A: Initially, the RTCM (Radio Technical Commission for Maritime Services) Subcommittee (SC104) Version 2 standard was developed with marine DGPS as the target application. One of the design goals for the RTCM SC 104 standard was to have correctional information readily available for user equipment. The outlines of the messages were specifically tailored for low bit rate data links.
Not until the beginning of the 1990s did RTK (real-time kinematic) surveying applications come into focus for RTCM. The committee drafted new RTK messages based on the proven DGPS messages. Although the DGPS messages only contain corrections, the RTK messages also allow transmission of raw observables from the satellite signals. RTCM tentatively published redundant means of disseminating precise RTK information with the aim of gaining practical experience during their implementation.
The first implementations by different manufacturers had diverse interoperability issues. For instance, various manufacturers have different sign conventions for representing the carrier phase observations, which resulted in incompatibilities when mixing receivers of different manufacturers.
(For the rest of Dr. Hans-Jürgen Euler’s answer to this question, please download the complete article using the PDF link above.)
Q: What is the probability of correctly resolving integer ambiguities and how can it be evaluated?
A: Resolving, or “fixing”, carrier phase ambiguities to integer values is ultimately based on statistical assumptions and testing. As such, a probability is associated with resolving any particular ambiguity correctly. Evaluating the probability of correct fix (PCF), that is, the probability that the ambiguities are fixed to the correct integer values, is particularly important for safety-critical applications where an incorrect ambiguity fix would produce hazardously misleading information (HMI).
In fixed-ambiguity carrier phase processing, the usual procedure is to begin by estimating the carrier phase ambiguities as real-valued (“float”) parameters and then to determine their integer values. A difficulty with this method is that, although the least-squares adjustment or Kalman filter used to estimate the real-valued ambiguities provides an estimate of their quality (a covariance matrix), it is not obvious how to obtain an estimate of the quality of the integer ambiguities.
In most carrier phase ambiguity estimation methods, integer quality is validated using some sort of statistical test. These generally involve testing the least-squares sum-squared residuals of the best fitting integer solution against the second best fitting solution. The test statistic is then compared against a threshold value, the idea being that if the best solution is sufficiently better than the second-best solution, then it must be correct.
(For the rest of Kyle O’Keefe and Mark Petovello’s answer to this question, please download the complete article using the PDF link above.)