This article focuses on the research project Galileo Online: GO! – which with support from the Federal Ministry for Economic Affairs and Energy (grant number 50NA1510) designs and develops a reliable and high-precision receiver for multi-constellation and dual-frequency GNSS whose suitability and capabilities are tested in railway applications. Project results showcase the advantages of GPS and Galileo if used simultaneously in railway applications.
In the rail sector, the state-of-the-art localization of trains is determined by track-side equipment, which is expensive and a general cost driver for rail transportation. In order to reduce infrastructural costs and to enable new safety critical applications and non-safety critical business cases, a reliable but infrastructure-independent positioning system is required. Challenges of such a system include achieving high accuracy, robustness, and availability of train localization even under harsh environmental conditions. For these purposes, the use of satellite-based navigation systems is a viable option, especially the parallel use of both GPS and Galileo signals.
For GNSS data integration, a preprocessing is required, which corrects e.g. signal delays caused by passing the ionosphere. For satellite measurements the positioning error caused by ionospheric path delay at daytime is in average up to 45 meters (See BDStar Navigation BeiDou Application the Omni-Directional Service Business, Additional Resources). In the case of using GPS with one single frequency, the well-known Klobuchar correction model provides corrections of approximately 50 % in average (Kaplan and Hegarty, Additional Resources). However, Klobuchar is not suitable for highly precise localization, especially not for satellites with low elevation angles. In turn, very accurate corrections can be performed by means of differential correction distributed by surrounding ground stations. These corrections can be received via mobile communication and are only provided for a fee in most cases. To cover situations even without local reference stations available, with poor mobile connectivity, or to avoid the use of expensive correction data, the present work investigates the use of multi-constellation with dual-frequency as a viable alternative. Therefore, this article introduces dual-constellation and dual-frequency GNSS-navigation using both GPS and Galileo signals.
This article reviews the work within the GO! project in developing a navigation filter, which is capable of processing dual constellation – the parallel usage of GPS and Galileo signals – in combination with dual-frequency signals. The filter bases on quantities of an inertial measurement unit (IMU), which are tightly coupled with observables of GPS and Galileo inside a filter algorithm. In this context, tightly coupled means the processing of inertial measurements corrected by the raw GNSS (Global Navigation Satellite System) observables with lower sample rate. In contrast, a loosely coupled filter determines its GNSS-only position and velocity first to correct IMU measurement in a straightforward manner. A tightly coupled filter allows a state correction even if less than four satellites are available. Due to the usage of satellite raw data, it is possible to evaluate each GNSS observable, to correct or even to exclude it.
The dual-constellation mode in general enhances the satellite availability because of an increased total number of available satellites and therefore, improves the geometrical constellation. Dual-frequency enables precise first-order ionospheric path delay elimination. Multiple real-world tests were carried out comparing the attained accuracy of the dual-constellation aided filter to differential corrected GNSS observables (DGPS). Results show that a 2D accuracy of up to 0.6 meters is achieved using the dual-constellation mode, which is almost as accurate as a filter using differentially corrected GPS.
Tightly Coupled Navigation Filter
Our tightly coupled filter bases on IMU quantities, where 3D accelerometer and 3D gyroscope measurements at a rate of 100 hertz are used within a well-known strap-down algorithm to propagate the filter states. The navigation filter estimates 18 states in total:
![]()
where position p, velocity v, and biases of the accelerometers ba and gyroscopes bg incorporate three components each, attitude and heading are defined as a quaternion q, and the GNSS receiver clock error consists of an offset cb and a drift cd component.
To provide long-term stability of the state propagation step, GNSS observables at a rate of 10 hertz are used to correct the drifting filter states. During a GNSS pre-processing step the received satellite ephemeris is used to calculate satellite positions at the time of signal transmission. Pseudo-ranges, deltaranges and satellite positions are used within an error-state extended Kalman filter (EKF), which estimates the error of the current propagated state vector based on a measurement model and updates the estimated state error and covariance matrix P. This results in a 6-DOF nonlinear model as follows:
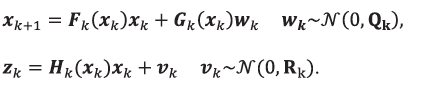
Here, k is the time index, x is the state vector of the system, w is the process noise, z is the measurement, and v is the measurement noise. w and v are assumed to be normally distributed with a mean of zero, where Q is the covariance matrix of the process noise (in this case the IMU noise) and R is the covariance matrix of the measurement noise included in GNSS observables. F, G and H are the state transition, noise and measurement matrices, respectively.
The usage of a digital receiver time pulse (pulse per second; PPS) allows measuring the time delay between measurement epoch and data reception on the target platform. It enables the synchronization of IMU data with GNSS observables. By introducing a data buffer for the IMU measurements and the past states, the Kalman filter update step can be performed with the (past) state at the time of measurement with a subsequent propagation to the present time. This approach improves the accuracy for highly dynamic movements.

Satellite Data Pre-Processing
Our EKF requires satellite position, relative velocity, and pseudo-and delta-ranges for all observed satellites. Therefore, satellite raw data is pre-processed to calculate the required system states for the EKF. Figure 1 sketches the applied structure of GNSS pre-processing.
The satellite signals are disturbed by several environmental influences causing biased pseudo-range measurements. The main influences can be summarized as ionospheric and tropospheric delays. The observed pseudo-range ρr can be described with the equation:
![]()
It is the sum of the real range , the satellite and receiver clock errors cS and cr , the ionosphere error
![]()
the troposphere error Tr and additive measurement noise vρ. Mρ is the multipath error, which is not corrected currently. The receiver clock error cr is dynamically estimated by the EKF. Both the GPS and the Galileo satellites transmit Kepler parameters. Therefore, position and velocity calculation and clock correction algorithms for GPS and Galileo are identical.
The GPS and Galileo radio propagation delay, caused by the ions of the ionosphere, is estimated assuming the delay as a first order frequency-depended function, for details see Gehrt et alia, Additional Resources. Therefore, this approach evaluates the received satellite signals and selects all satellites providing in dual-frequency mode.
In some cases, some satellites do not provide two frequencies. For example, when older GPS satellites or the receiver is not able to receive more than one frequency of a particular satellite due to environmental circumstances. In this case, the well-known Klobuchar model for GPS measurements is used to correct ionospheric delays. Tropospheric delays for both systems are calculated by a common mapping function, first presented in a paper by Collins (Additional Resources).
If available, differential corrections are preferred to increase the quality of the correction information. In this case, the correction models for ionospheric and tropospheric delays are replaced. The correctional data is received from a network of reference stations. They provide GPS observables and precise coordinates of a virtual base station close to the current user position. Currently this service is available for GPS only. Therefore, this mode is currently applied during GPS pre-processing only and will be extended for Galileo in the near future. The correction approach reduces the expected error standard deviation in GPS pseudo-range observables below 1 meter. (Farrell and Mohinder et alia, Additional Resources).
Dual-Constellation Extension
Processing GPS and Galileo observables of the same receiver and within a single navigation filter requires a synchronization
of both satellite system clocks. This synchronization was applied by introducing an extension in the GNSS pre-processing by Gehrt et alia at proceedings of the 2018 International Technical Meeting of The Institute of Navigation.
Therefore, the EKF receives observables with the same clock source, which allows estimating one clock error and drift within the state estimation. As clock source, GPS or Galileo is defined as reference system. Furthermore, it is assumed, that the pseudo-range measurements of the secondary GNSS system contain an additional artificial signal transmission error Δssystem , such that eq. (4) is extended as follows:
![]()
Δssystem can be interpreted as the product of the speed of light and the time difference Δtsystem between the reference system clock and the clock of the secondary system. In the case of GPS and Galileo, both clocks are real-time steering realizations of UTC (Hahn and Powers, Additional Resources). Therefore, it is assumed that Δtsystem is small and in turn Δssystem can be neglected within the GNSS pre-processing step. This results in a simpler downstream architecture, where the GNSS pre-processing is first executed followed by the described synchronization step.
Results
In order to validate the enhancements of the conducted multiconstellation extensions and its online capability, extensive measurement campaigns are performed within realistic railway environments. In the experimental validation, the online-capable navigation filter with three different settings with respect to the pseudo-range correction is evaluated and compared. The first setting corrects the ionospheric error of the pseudo-ranges of GPS L1 observables with the Klobuchar-Model. Setting two applies ionospheric corrections by means of dual-frequency approach in dual-constellation mode. These settings utilize the tropospheric correction model. The third setting performs differential corrections, which takes both the ionospheric and the tropospheric errors into account.
Zweigel et alia (Additional Resources) previously presented filter results in 2017. Herein, a best-case environment was
chosen with little infrastructural obstacles and low system velocity. As expected, the navigation filter aided with GPS L1 observables and Klobuchar ionospheric corrections provides low accuracy due to the low quality ionospheric corrections. In comparison, the 2D precision of the dual-constellation mode with dual-frequency correction could be improved to a position error lower than 0.4 meters. This result is within the range of the high accuracy of GPS L1 with differential corrections.
Additionally, extensive tests have been carried out in the railway test center Pruef- und Validationscenter Wegberg-Wildenrath (PCW) of the Siemens Company in Germany (Gehrt et alia, Additional Resources). Results confirm the comparable 2D accuracy of the dual-constellation mode compared to differential mode with an accuracy lower than 1 meter. Therefore, track-resolved train localization using the presented navigation filter could be proved.
Another test campaign has been performed, aiming on proving the high accuracy even during long duration tests in harsh railway environment. Figure 2 shows a general overview of the designated test track in Bavaria, Germany, which could be used thanks to the Chiemgauer Lokalbahn LEO from Bad Endorf to Obing. The test track is approximately 20 kilometers passing through urban environment, hills, and forest. The colored trajectory visualizes the whole track. The blue colored sub-track is the part which is evaluated here.
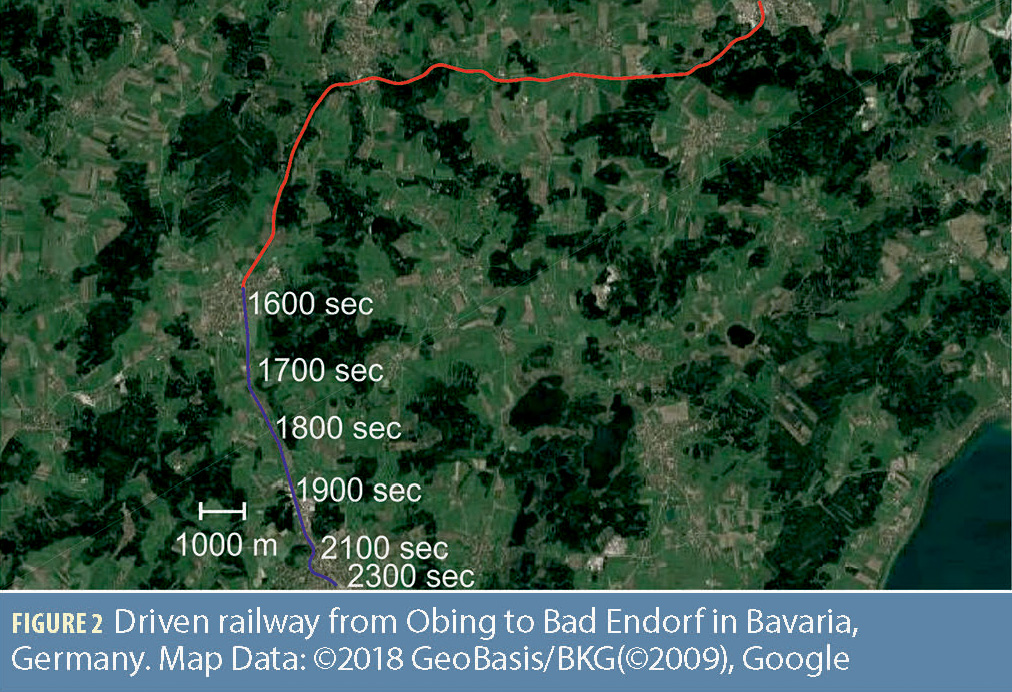
Figure 3 gives an impression of the test campaign conditions with high conifers close to the single rail track. Due to the season, the trees are covered with snow, causing signal reduction, attenuation, and signal shadowing. Furthermore, sections surrounded by farmland are covered with dry snow causing signal reflection and multipath effects.

During all tests, the measurement noise of the GNSS observables is calculated using a function of the Signal to Noise Ratio (SNR) measured by the receiver. For the navigation filter’s differential mode, the correction data is received in RTCM-V3 format using the N-trip protocol via broadcast. Due to poor internet connectivity, especially along the middle part of the test track, a continuous update of differential data cannot be guaranteed. Since Konrad et alia (Additional Resources) proved the RTK suitability as reference system for static and dynamic conditions, a RTK capable receiver is used for reference purposes. The platform on which the navigation filter is running is a Rapid Control Prototyping (RCP) system for real-world evaluation tests. The RCP realtime hardware is a 900 megahertz single core system.
For inertial measurement, the setup utilizes an industrial-class IMU-sensor that provides accelerations, angular rates and magnetometer measurements at a rate of 100 hertz. A receiver provides the required GNSS observables with an update rate of 10 hertz. The communication link between these two devices is realized via serial interface. In addition, communication and process delays can be determined and compensated using a PPS signal.
Figure 4 provides the evaluation results of the test campaign. The first plot gives the 2D-error of the three introduced GNSS pre-processing modes. Here, the 2D error means the difference between the EKF solution and the position of the reference system. The accuracy of this 2D-error calculation depends on the accuracy of the reference system. Therefore, the fourth subfigure gives the mode of the reference receiver, which switches between the precise RTK fix and less precise differential GPS modes due losses in differential data updates. Switches of the reference receiver mode can result in jumps on the 2D-error. The second sub-plot shows the satellite availability of the GPS and the Galileo system.
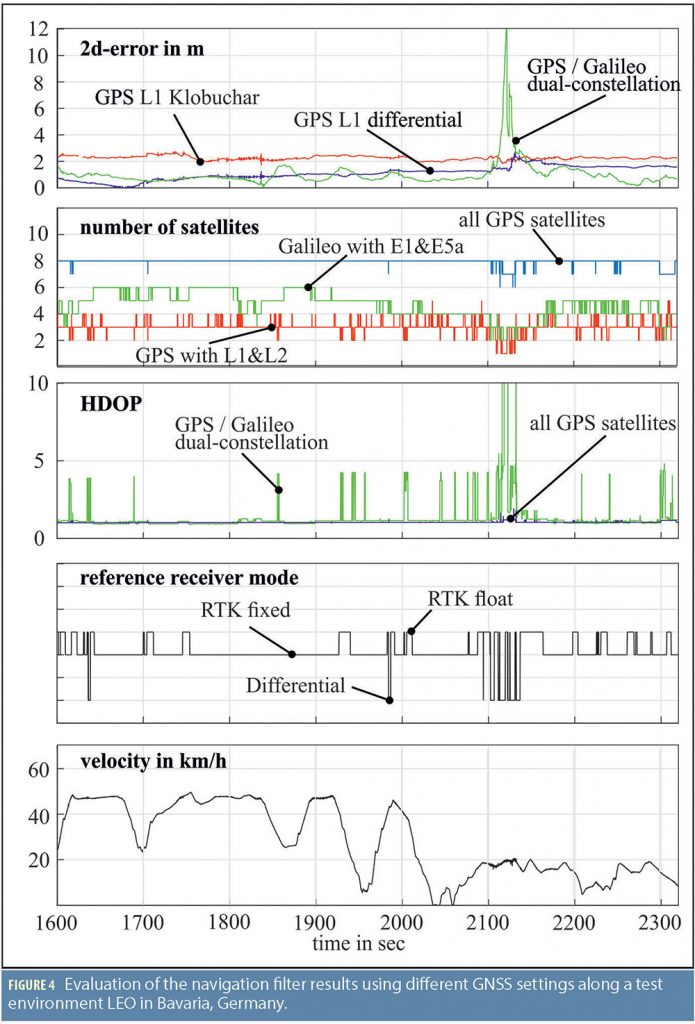
A closer look is taken on GPS and Galileo satellites, which are able to provide two frequencies and therefore, can be included in a dualconstellation with dual-frequency ionospheric correction. It is obvious that the rising number of available Galileo satellites just enables the exclusive use of dual-frequency satellites, when applying dual-constellation in combination with GPS. The corresponding Horizontal Dilution of Precision (HDOP) of the dual-constellation and for comparison of all available GPS satellites (within our elevation mask) is presented in the third sub-figure. In some instances, the available dual-constellation set of satellites only provides poor geometrical constellation. The vehicle velocity is given in the lower plot.
Compared to the results mentioned earlier from Zweigel et alia and Gehrt et alia, the 2D accuracy resulting in this last test campaign with respect to all three filter modes is of a slightly lower level. As expected, the accuracy of the EKF with GPS L1 observables and Klobuchar ionospheric correction is permanently in the range of more than 2 meters. Due to a temporary low number of available satellites and a resulting poor satellite constellation at i.e. second 1850, second 1930 and thereafter, the dual-constellation loses the high accuracy. It gets worse around second 2150, where only three satellites are available and HDOP rises towards infinity. Nevertheless, the total average accuracy is still below 1 meter and along some sections even better than the navigation filter with differential correction mode, which is in accordance with former measurement campaigns.
Summary and Outlook
The present work introduces the technical developments for the GNSS processing of an existing tightly coupled navigation filter as part of the ongoing research project Galileo Online: GO!. It presents Galileo enhancements with a dual-constellation approach and processing of differential data. The advantages of using GPS and Galileo in dual-constellation and processing two frequencies of each satellite are discussed and evaluated in extensive measurement campaigns in harsh railway environments. Obtained results prove that both the differential aided filter and the multi-constellation aided filter provide track-resolved position estimation, even under worst conditions. Moreover, results show that both modes are almost complementary. The huge advantage of the dual-constellation mode consists in the independency of differential corrections broadcasted via mobile radio.
For future works, a state machine, which enables switching between the available filter modes regarding current conditions, is in progress. Poor GNSS reception, signal damping, and multipath effects in combination with high requirements on the position estimation, reveal a wide field for future research on GNSS signal integrity determination. Developments, basing on well-known Receiver Autonomous Integrity Monitoring (RAIM) algorithms, applied on dual constellations with Fault Detection and Identification (FDE), methods are in progress.
Manufacturers
The RCP real-time hardware referenced in the Results section is a MicroAutoBox II, with a 900 megahertz single core system from dSPACE, Paderborn, Germany. For inertial measurement, the setup utilizes a LORD MicroStrain 3DM-GX4-25 industrial-class IMU-sensor from LORD Sensing, Williston, Vermont. A Septentrio AstRx3 HDC receiver from Septentrio, Leuven, Belgium and Torrance, California, provided the required GNSS observables with an update rate of 10 hertz.






