Q: Would you prefer to have more signals or more satellites?
A: This is somewhat of a classic GNSS question, but before getting to the answer, let’s seek some clarity about what is being asked. First, by definition, “more” signals or “more” systems must be referenced against some baseline configuration. This is commonly assumed to be a GPS L1 C/A solution, and this assumption is also used herein.
Q: Would you prefer to have more signals or more satellites?
A: This is somewhat of a classic GNSS question, but before getting to the answer, let’s seek some clarity about what is being asked. First, by definition, “more” signals or “more” systems must be referenced against some baseline configuration. This is commonly assumed to be a GPS L1 C/A solution, and this assumption is also used herein.
Second, “more signals” is most commonly interpreted as meaning more frequencies for a given GNSS (e.g., using GPS L1 C/A and L2C), and “more satellites” is typically interpreted as using additional GNSS relative to the baseline case (e.g., GPS and GLONASS, or GPS and Galileo).
Returning back to the original question, as is the case for so many GNSS questions, the answer is: it depends. It depends primarily on the operating environment and the desired positioning accuracy, although other issues may also be critical factors.
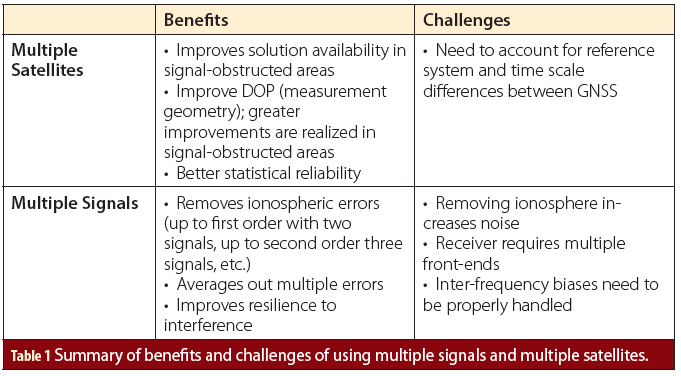
By extension, there is no one-size-fits-all answer to this question. Instead, below is a summary of the benefits and challenges of having more signals and having more satellites. I adopted this approach with the hope that readers will better appreciate the trade-offs between the two approaches such that they can make decisions for their specific applications.
More Satellites
Having more satellites is generally most useful when satellite visibility is reduced, such as in deep urban areas. In such cases being able to track signals from multiple GNSS makes it more likely to be able to compute a solution at all. That is, a multi-GNSS approach improves solution availability.
However, even if a single-GNSS solution were possible, having data from multiple GNSS will yield better measurement geometry, or lower dilution of precision (DOP) values. In turn, this results in more precise position estimates.
Having measurements to more satellites also allows the position filter to be more selective about the measurements to be used. For example, ongoing research is investigating how to use carrier to noise-density ratio (C/N0) information, 3D building models, cameras, or some combination of these to determine when a received signal does not contain a line-of-sight (LOS) component. These satellites can then be rejected leaving, hopefully, only LOS signals—or perhaps multipath-corrupted LOS signals—to derive a more accurate position estimate. To realize the full benefit of such approaches there needs to be enough LOS-based signals available to compute a solution. It follows that the probability of this happening increases as more GNSS are used.
Multi-GNSS approaches also offer accuracy benefits in less benign environments, but to a lesser extent. The reason for this is because in the absence of large errors arising from non-LOS (NLOS) or multipath signals, the main benefit is in terms of improved geometry. But the absence of (many) NLOS signals suggests good sky visibility, in which case even the baseline configuration of a single-GNSS solution will typically have reasonable geometry already.
Since DOP is approximately proportional 1⁄√N to where N is the number of satellites used, doubling the number of satellites only provides about 30% reduction in DOP, but tripling the number of satellites reduces DOP by only 42%. Although always beneficial, it is obvious that adding more and more satellites offers diminishing returns.
Unrelated to position accuracy, using more satellites will improve the statistical reliability of the system. In other words, a multi-GNSS solution is more likely (in terms of a probability) to identify a measurement blunder of a certain magnitude than is a single-GNSS solution. Equivalently, a multi-GNSS solution will be able to identify smaller blunders than a single-GNSS solution with the same level of probability.
Although the details of this are beyond the scope of this article, the reason for this is that the magnitude of blunder that can be detected at a given probability level is dependent on geometry which, as described above, is better with multi-GNSS solutions.
On the downside, multi-GNSS solutions need to properly handle differences, if any, in reference ellipsoids (e.g., WGS48 for GPS and PZ-90 for GLONASS) and time scales between the different GNSS. This is not particularly difficult, but ignoring such effects can have significant impacts on positioning performance. Of particular note is that extra states may need to be added to the position filter to properly account for timing differences.
Before moving on, it should be noted that if many satellites are being tracked but the receiver’s processing resources and/or power are limited, it may be desirable and/or necessary to only process a subset of all possible satellites to minimize power consumption. Such situations are likely to be uncommon (and much more enviable than other GNSS-related challenges), but selecting which satellites to process will need to consider the trade-offs between processing complexity, solution precision and statistical reliability.
More Signals
The main benefit of using multiple signals is improved accuracy. This happens in two ways: mitigating ionospheric effects and, to a lesser extent, minimizing multipath effects.
It is well known that ionospheric errors, I, are a function of the carrier frequency of the signal passing through the medium
I(f) = 40.3 x TEC/f 2
where TEC is the total electron count in a square-meter cross-section along the signal path and f is the signal’s carrier frequency. This dispersive quality allows measurements from two signal frequencies to correct for the first-order ionospheric effects. This accounts for typically 99% of the errors, but using three (or more) frequencies allows for the removal higher-order effects.
The downside of this approach is an increase in noise arising from the combination of multiple noisy measurements, for example, noise increases nearly three-fold when using GPS L1 and L2 measurements.
Ionosphere error minimization is the primary benefit of using multiple signals. Practically, however, this benefit is only realized if ionospheric errors represent a significant part of the error budget. This would include situations where multipath effects are limited and/or for real-time kinematic positioning with carrier phase data to improve ambiguity resolution.
For pseudorange-based systems, the benefit of removing the ionosphere will depend largely on the level of measurement noise; if the noise is too high relative to the ionospheric error, then there may be little practical benefits to be realized. That said, increased measurement noise is zero-mean and can be reduced with sufficient averaging/filtering, if the application allows.
Having multiple signals can also be helpful at minimizing the effect of multipath when the LOS signal is present (this contrasts with scenarios where there is multipath but all paths are NLOS). In such cases, the reflected paths are the same for both signals, meaning they both have the same path delay. However, the phase difference between the LOS and NLOS signals at the receiver is generally not the same and so averaging across signals offers some benefits, especially if one of the signals has a large multipath effect.
Of course, if the LOS signal is not present, then there is no benefit since the LOS signal cannot be recovered.
In theory, a multi-signal approach will also improve the statistical reliability of the solution. Practically, these improvements are minimal because GNSS measurement blunders typically arise from multipath and such errors (albeit with different magnitudes, as discussed above) are present on all signals from a given satellite. With this in mind, it should be intuitively obvious that using a blundered measurement to detect a blunder in another measurement does not typically yield the desired result.
The final benefit of multiple signals is the improved resilience to interference. This arises from the simple fact that jamming two or more signals in different bands is inherently more difficult than jamming a single frequency. If the additional signals also have ranging codes with wider bandwidths and/or different auto-correlation properties, this can further improve interference mitigation—this latter benefit would therefore be realized for multi-GNSS systems as well.
The challenges of using multiple signals are two-fold. First, the receiver will need two front-ends, which in turn requires more power. This will be especially important for power-sensitive applications. Second, inter-frequency biases need to be properly accounted for. Most receivers already calibrate these but this is nevertheless a source of error.
Summary
Table 1 (at the top of this article) summarizes the benefits and challenges of each of the two scenarios discussed above. Broadly speaking, if you have to choose between the two approaches, multi-GNSS systems will be most beneficial in signal-obstructed the receiver is not ideally located on the object being positioned (e.g., inside a car or inside a bag). In contrast, multi-signal systems will typically be most useful for improving accuracy when signal visibility is less of a concern. areas such as urban canyons or when
That said, GNSS applications vary widely in terms of their requirements, operating environments, or both. It is the responsibility of the system designer to consider the benefits and challenges of the different approaches in order to maximize performance for their application.
Of course, the most desirable option would always be to use a multi-signal, multi-GNSS system, if possible.