Why the timekeeping and GNSS communities should start preparing.
DEMETRIOS MATSAKIS, MASTERCLOCK
DENNIS MCCARTHY, U.S. NAVAL OBSERVATORY, CONTRACTOR
Although the public is largely unaware of it, we have for the last 50 years been adding a second to the time occasionally, worldwide, as a consequence of the fact the Earth does not rotate perfectly uniformly.
The concept of the diurnal rotation of the Earth had been suggested in ancient Greece and accepted by several early Greek philosophers [1] but it remained unproven rigorously until the demonstration by Leon Foucault using his pendulum in 1851 [2]. The constancy of the Earth’s rotational speed was assumed until the 17th century when astronomical observations began to reach a higher level of accuracy and analyses by Halley and Newton cast doubt on that assumption [3]. In the 1860s, William Ferrel [4] and Charles-Eugène Delaunay [5] were able to show independently that lunar ocean tides exert a secular retarding action on the rotation of the Earth.
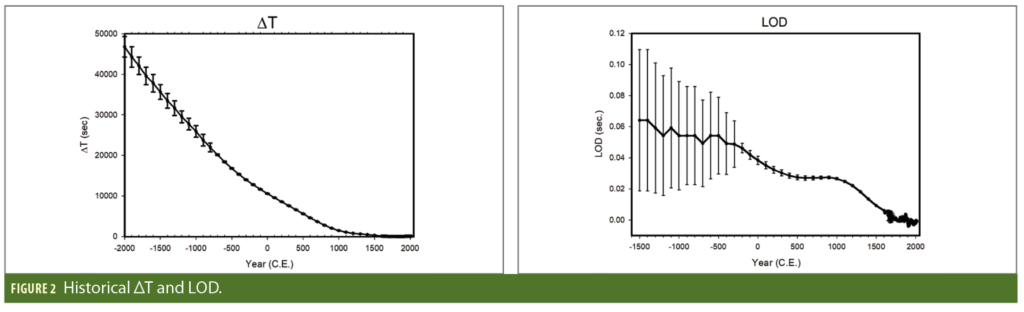
Pre-historical estimates of the variations of the length of the solar day can be inferred from fossil records [6], and the recorded occurrences of observations of solar eclipses provide historical estimates as well (Figure 3). These estimates are based on the difference in time between a uniform time and the local solar time now called Universal Time (UT). The uniform time, now called Terrestrial Time (TT), is based on the independent argument of time in the gravitational theories of the motion of solar system bodies or, in recent times, by atomic clocks calibrated to match time inferred from those theories.
Factors Influencing the Earth’s Rotation
While the slowing of the Earth’s rotation can be attributed largely to the tidal interaction of the Earth’s oceans with the Moon, several other factors have an influence. The warming of the Earth since the ice ages has caused glaciers to melt so the underlying polar land mass rises while the equatorial regions settle, making the Earth rounder. This effect, termed glacial isostatic adjustment, causes the Earth to rotate faster. While these two phenomena are the most significant contributors to the long-term changes in the Earth’s rotational speed, there are decadal variations apparently due to movements of mass within the Earth and which are being studied through earthquake and geomagnetic observations [7].
On a shorter scale, seasonal variations influence the Earth’s rotation. They were detected as early as 1936 by comparing astronomical observations of solar time with quartz crystal clocks [8]. Other high-frequency variations in the Earth’s rotation became extremely obvious after the invention of atomic clocks, the development of International Atomic Time (TAI), and the development of more accurate means to measure astronomically-based time, UT1. The latter include Lunar Laser Ranging (LLR), Very Long Baseline Interferometry (VLBI), and even analyses of the orbits of Global Navigational Satellite Systems (GNSS) [9,10].
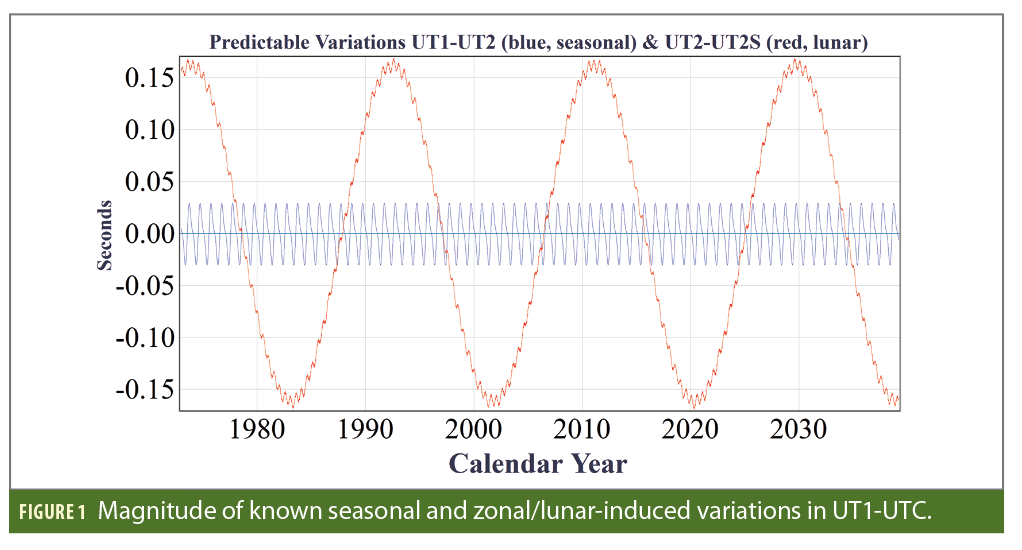
The excess length of day (LOD) is the derivative of TT-UT1, and it is typically expressed as a deviation from its nominal value of 86,400 SI seconds. Tidal and seasonal phenomena are predictable enough to be approximated by standard models in the IERS Conventions [11]. UT2 is defined as UT1 after the predictable seasonal effects are removed, and UT2S is defined as UT2 after predicable lunar and zonal atmospheric effects are removed from UT2. Analogously, LOD2S corresponds to the derivative of TT-UT2S. Chief among the lunar effects are the 14-day (half-orbit) periodicity of the Moon and the 19-year Metonic cycle of its orbital obliquity. Figure 1 shows the magnitude of these periodic terms.
Time Deviations
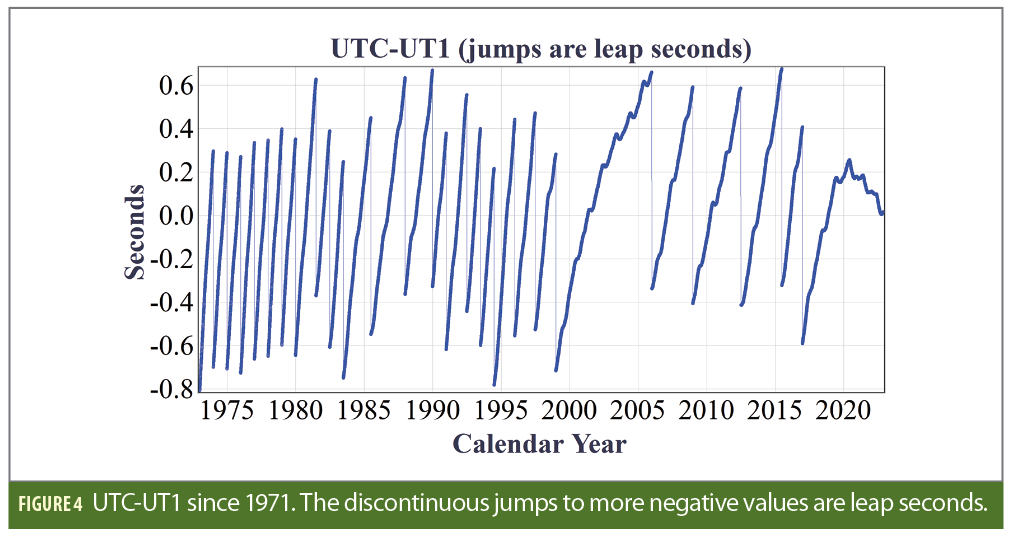
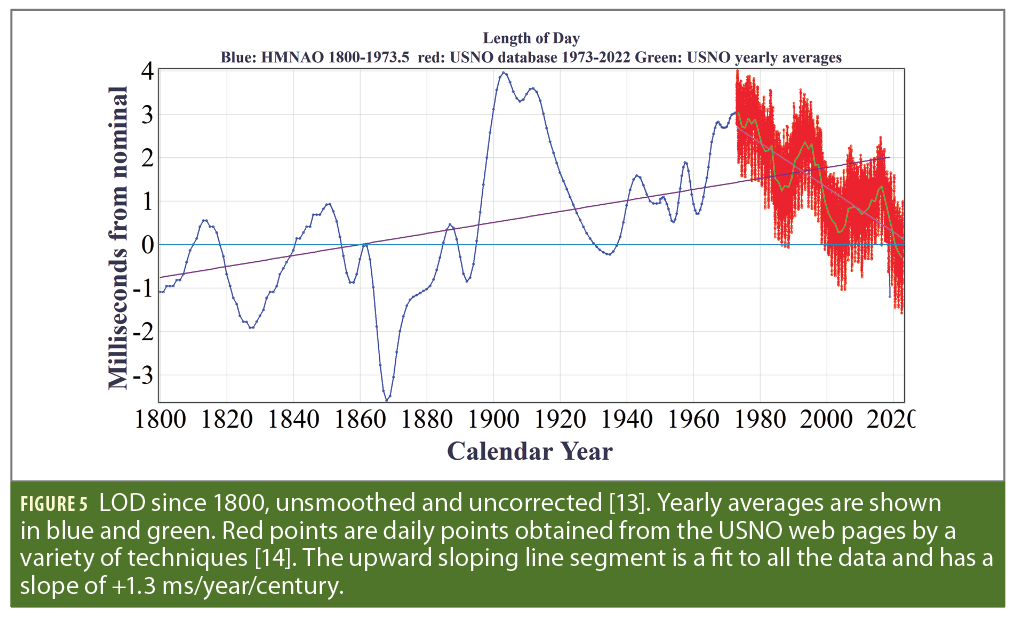
In 1970, it was decided to define the standard unit of time, the Système International (SI), or International Second, strictly in terms of the hyperfine atomic transition of Caesium-133, and to establish Coordinated Universal Time (UTC) as the worldwide operational time standard [12]. The epoch of UTC would be adjusted by one-second increments (leap seconds) as necessary to maintain synchronization with the Earth’s rotation so that |UTC-UT1|<0.9 seconds. This discontinuity could be introduced at the end of any month, as determined by the International Earth Rotation and References Systems Service (IERS) with preferences being the end of June or the end of December. Figure 2 shows the ΔT=TT-UT1 and the excess length of day (LOD) compiled by [13] using observations from 2000 BCE until 2015 CE.
Although TAI-UT2S shows less variations than TAI-UT1 or TAI-UT2, they have some common structure. On timescales less than two years, their unpredicted variations can be attributed largely to the atmospheric angular momentum variations, which strongly anticorrelate with the angular momentum (rotation) of the Earth’s crust. In fact, the predictions of crustal rotation rate generated by the U.S. Naval Observatory (USNO) for GPS operations are largely based on predictions of the atmospheric angular momentum [14, 15]. On decadal timescales, the LOD (and with it UT1, UT2 and UT2S) can fluctuate because of uneven braking as the torques experienced by the crust are passed into the Earth’s interior, and to a much lesser extent because of the shape of the Earth changing from recent global warming [16].
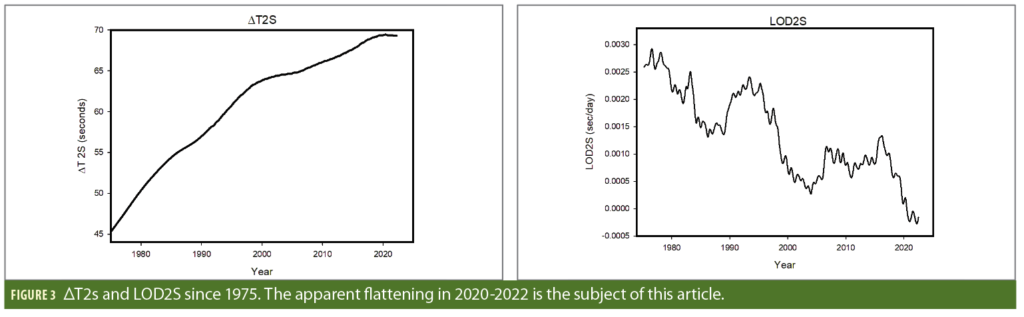
Our understanding of these decadal fluctuations is largely based on data from the pre-atomic days, reduced using the Moon’s orbit to create a proxy for TAI/TT. Figure 5 shows available data since 1800, which are suggestive of a random walk (RW) process. The data are averaged but not smoothed, and the large long-term variations are the decadal fluctuations. The pre-1950 data are yearly averages, while the 1950-1971 points are six-month averages. The data since 1971 are daily points, and their large apparent jitter is largely due to the 14-day lunar cycle. The yearly averages of those daily points are shown in green. The historical slow-down of 1.4 ms/day/century is fully obscured by the decadal variations, although a least-square fit to the yearly points yields a value close to that.
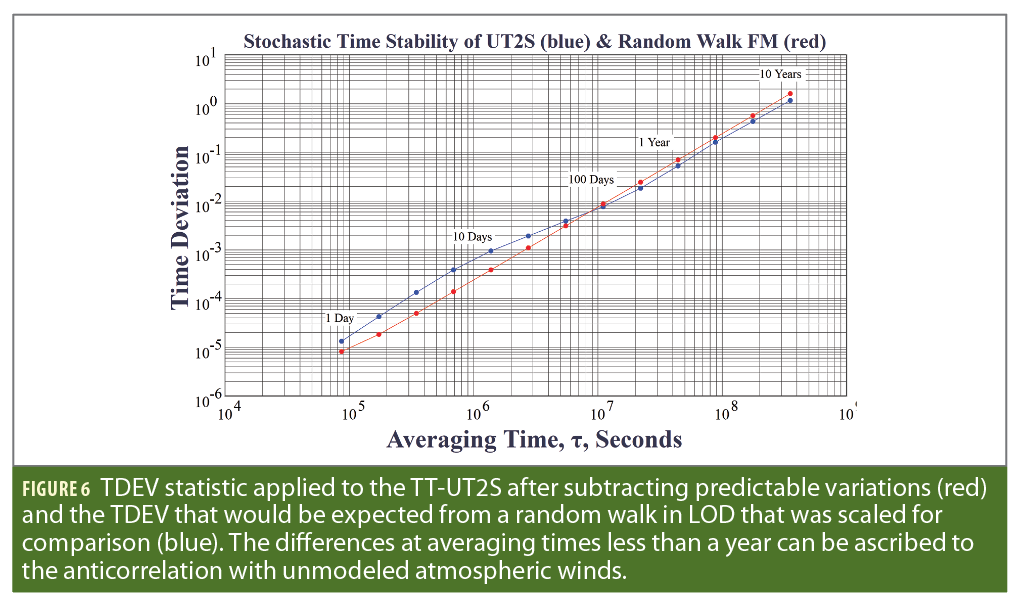
The LOD timeseries of Figure 5 can be analyzed using the Time Deviation (TDEV) statistic σx, which is a measure of the variations of any time series. In the case where the derivative of the time series is characterized as a random walk, the time deviation is expected to have a slope of +1.5 on a log-log plot of σx versus τ [17].

The TDEV plot of the TT-UT2s data is shown in Figure 6, along with what would be expected if the LOD timeseries was a RW scaled to agree at the large τ. It is evident that the actual LOD data behave very much like a RW for timescales larger than a year. Unpredictable atmospheric effects are the likely source of deviations on the shorter scales.
Predicting Rotational Behavior
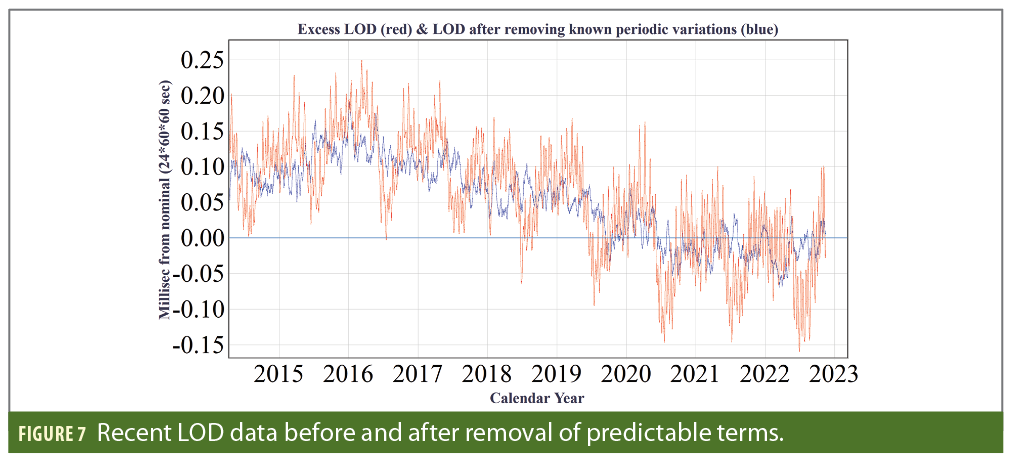
The strategies used to predict Earth rotational behavior for the next decade start with removing all of the known deterministic effects to obtain TAI-UT2S. Figure 7 shows the derivative of the most recent TAI-UT2S data, along with the derivative of the TAI-UT1 data. These derivatives are the LODs with and without the predictable variations.
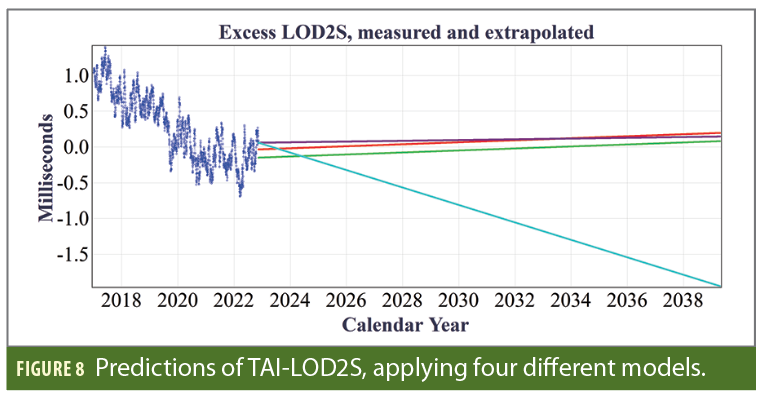
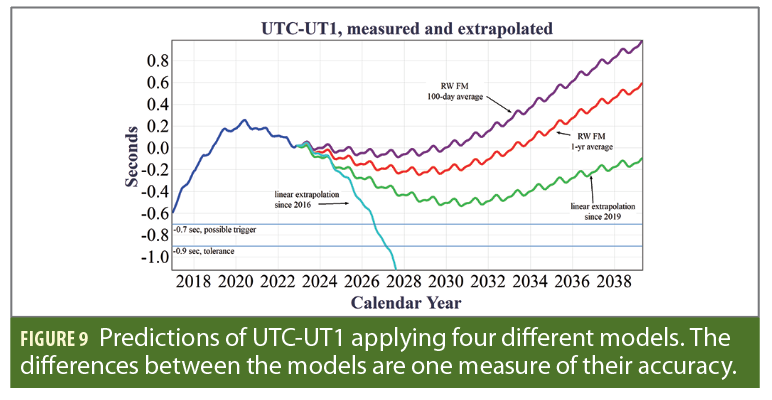
Predictions extending a few years into the future do not entirely enter the regime where a RW would dominate. Therefore, two predictive models are employed, each with two variations. In the RW family of models, the best predictor of future data is the most recent datum (because the derivative of a RW is white noise, equally likely to be negative as positive). Given the need to smooth over short-term variations, the current value of the RW is taken as either the average over the last year, or as the average over the last 100 days. A second family of models simply assumes that the linear trends observed in the LOD will continue for the entire predictive period. Here again, two subfamilies are employed. One is a linear extrapolation of the LOD from January 1, 2016, to today, and the other extrapolates only over the last three years. In all cases, the extrapolations are integrated to form TAI-UT2S predictions, which are then converted to UTC-UT1 predictions by adding back the predictable corrections. Figures 8 and 9 show the results of the four extrapolations in the LOD2S and UTC-UT1. These plots are based on data made public by the IERS Rapid Service/Prediction Centre on February 8, 2023.
In these curves, the general uptrend after 2030 is largely due to the Metonic cycle. There is also the accumulated effect of the long-term historical slowdown, which integrates to about 0.25 seconds in a decade. It is important to realize that each extrapolation, even within the context of its own assumptions, does not indicate a highly likely outcome. Rather, each curve indicates the median behavior of its range of possible outcomes. An additional uncertainty is what extrapolated value or trend of UTC-UT1 will be considered by the IERS to be the proper one to trigger a negative leap second, given the need to announce it well in advance and the possible disruption it might cause. In this plot, a possible trigger value of -0.7 seconds is shown solely because in the past leap seconds have been inserted so UTC-UT1 would reach that level. Given the concern about the possible effects of a negative leap second, they may decide to go closer to the tolerance.
Conclusion
The chief conclusion of our analysis is that we are almost as likely as not to experience a negative leap second in the next 12 years. We also note that the General Conference on Weights and Measures (CGPM) adopted a resolution in November, 2022 [18], calling for the tolerance for |UTC-UT1|to no longer be fixed at 0.9 seconds, but rather be determined after due consideration of the needs of the stakeholders [19]. While the tech giants Meta (Facebook), Amazon and Microsoft have recently joined the U.S. and many other governments in calling for the abolition of all future leap seconds as quickly as practical, and although the CGPM resolution calls for a change to be made before or in 2035, it is widely anticipated that it would be more likely in 2035. Therefore, the possibility of a negative leap second is very real. The timekeeping and GNSS communities need to check their software and hardware for possible breakdowns due to positive or negative leap seconds, both by inspection and with testing. In such testing it would be important to test entire systems as well as individual components [20].
References
(1) McColley, Grant, 1937, “The Theory of the Diurnal Rotation of the Earth” Isis, 26, 392-402.
(2) Foucault, L., 1851, “Démonstration physique du mouvement de rotation de la terre au moyen du pendule,” C. R. Acad. Sci. 32, 135-138.
(3) McCarthy, D. D. and Seidelmann, P. K., 2018, Time: From Earth Rotation to Atomic Physics 2nd Edition, 400 pp.
(4) Ferrel, W., 1864, “Note on the Influence of the Tides in Causing an Apparent Secular Acceleration of the Moon’s Mean Motion,” Proc. American Acad. Arts and Sciences, 6, 379-383.
(5) Delaunay, C.-E., 1865, “Sur l’existence d’une cause nouvelle ayant une action sensible sur la valeur de l’équation séculaire de la Lune,” Comptes rendus hebdomadaires des séances de l’Académie des sciences 61, 1023-1032.
(6) N. J. de Winter, N. J., Goderis, S., Van Malderen, S. J. M., Sinnesael, M., Vansteenberge, S., Snoeck, C., Belza, J., Vanhaecke, F., Claeys, P., “Subdaily-Scale Chemical Variability in a Torreites Sanchezi Rudist Shell: Implications for Rudist Paleobiology and the Cretaceous Day-Night Cycle,” Paeloceanography and Paleoclimatology, 35, 5 Feb 2020.
(7) Yang, Y. and Song, X., “Multidecadal variation of the Earth’s inner-core rotation”, Nature Geoscience , 23 Dec 2023, https://doi.org/10.1038/s41561-022-01112-z
(8) A. Scheibe and U. Adelsberger, 1936, “Schwankungen der asronomischen Tageslange und der astronomischen Zeitbestimmung mit den Quarzuhren der Phys.Techn. Reichsanstalt, ” Phys. Z., 37, 185-203.
(9) Eubanks, T. M. 1993, “Variations in the Orientation of the Earth”, Contributions of Space Geodesy to Geodynamics: Earth Dynamics: Geodynamic Series, Volume 24. Edited by David E. Smith and Donald L. Turcotte. Washington, D.C.: American Geophysical Union, 1993., p.1.
(10) https://igs.org/products.
(11) IERS Conventions (2010), Gérard Petit and Brian Luzum (eds.). “(IERS Technical Note ; 36) Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie, 2010.” (“IERS – IERS Technical Notes – IERS Conventions (2010)”) 179 pp., ISBN 3-89888-989-6.
(12) Arias, F., Matsakis, D., Tavella, P., Quinn, T., 2018 “The Fiftieth Anniversary of the Atomic Second,” Trans. UFFC, 2018.
(13) Stephenson F. R., Morrison L. V., and Hohenkerk C. Y. 2016, “Measurement of the Earth’s rotation: 720 BC to AD 2015,” Proc. R. Soc. A., 472, id 20160404 http://doi.org/10.1098/rspa.2016.0404 .
(14) D.Matsakis “Predicting UT1-UTC, a work in progress”, report to the timing subcommittee of the Civil GPS Service Interface Committee, 2018, https://www.gps.gov/cgsic/meetings/2018/matsakis.pdf.
(15) N. Stamatakos, D. Salstein, and D. McCarthy, “IERS Rapid Service/Prediction Center Use of Atmospheric and Ocean Angular Momentum for Earth Rotation, EGU21, 2021, and references therein.
(16) Zotov, L., Bizouard, C., Shum, C. K., Zhang, C., Sidorenkov, N., Yushkin, V., 2022, “Analysis of Earth’s polar motion and length of day trends in comparison with estimates using second degree stokes coefficients from satellite gravimetry,” Advances in Space Research, 2022, 69, pp.308-318. (10.1016/j.asr.2021.09.010). (insu-03713038).
(17) Barnes, J.A., Chi, A.R., Cutler, L.S., Healey, D.J., Leeson, D. B., McGunigal, T.E., Mullen Jr., J.A., Smith, W.L., Sydnor, R.L., Vessot, R.F.C. Winkler, G.M.R., 1971, “Characterization of Frequency Stability”, I.E.E.E. Trans. Instr. Meas., IM-20, No. 2, 1971.
(18) https://www.bipm.org/documents/20126/64811223/Resolutions-2022.pdf/281f3160-fc56-3e63-dbf7-77b76500990f.
(19) Levine, J., Tavella, P., and Milton, M., “Towards a consensus on a continuous Coordinated Universal Time”, Metrologia, open source, https://doi.org/10.1088/1681-7575/ac9da5,2022.
(20) At the Plugfest associated with the 2022 meeting of the International IEEE Symposium on Precision Clock Synchronization (ISPCS) it was found that one participant’s Device Under Test treated a negative leap second as a positive one. The cause was traced to the format of the Uni Erlangen time string, which does not allow for a negative leap second (Thomas Behn, private communication). This is why we test.
Authors
Dr. Demetrios Matsakis has been Chief Scientist for Masterclock, Inc. since his 2019 retirement as Chief Scientist for Time Services at the U.S. Naval Observatory (USNO). In his 40 years at the USNO, he worked on most aspects of precise timekeeping, including 16 years as Department Head. His first 18 years there were devoted to measuring variations in the Earth’s rotation using interferometry. More recently, he represented the U.S. at the ITU, in Geneva, where leap seconds was the main issue. Since retirement, he has worked on improving the USNO’s predictions of Earth rotation for GPS operations as a member of the Va. Tech faculty. In 2023 he won ION’s PTTI Distinguished Service Award. He is an editor for GPS Solutions, has published approximately 170 scientific papers, and secured one patent. His definition of time can be found on the Encyclopedia Britannica’s web pages.
Although officially retired from the U.S. Naval Observatory where he was Science Advisor, Director of the Directorate of Time, and Head of the Earth Orientation Department, Dennis McCarthy is now a contractor with the Observatory and a member of U.S. Working Party 7A of the International Telecommunications Union Radiocommunications Section. Internationally, he is the representative of the International Astronomical Union to the Bureau International des Poids et Mesures and Consultative Committee on Time and Frequency. He has served as President of the Commission on Time, Commission on Earth Orientation, and Division 1 (Fundamental Astronomy) of the International Astronomical Union (IAU). He was also secretary of Commission 5 of the International Association of Geodesy. He has been a chair of, and member of, various working groups within the IAU and the author and editor of publications dealing with fundamental astronomy, time and Earth orientation.






