Government agencies and private industry worldwide are advancing toward a sustained presence on the Moon. In response, NASA, ESA and JAXA are collaborating to develop LunaNet—a network of cooperating networks designed to provide robust and interoperable lunar communications and PNT services.
PHILIP DAFESH, GOURAV KHADGE, NATHAN WONG, GORAN DJUKNIC, THE AEROSPACE CORPORATION JUAN M. CRENSHAW, CHERYL J. GRAMLING, BRIAN C. PETERS, NATIONAL AERONAUTICS AND SPACE ADMINISTRATION (NASA) FLOOR MELMAN, RICHARD SWINDEN,
COSIMO STALLO, THE EUROPEAN SPACE AGENCY (ESA) MASAYA MURATA, JAPAN AEROSPACE EXPLORATION AGENCY (JAXA)
The build-up of LunaNet services is envisioned to provide a wide array of capabilities supporting future lunar exploration (Figure 1). This initiative aims to support the anticipated surge in lunar missions, including those associated with Artemis.
The LunaNet Interoperability Specification, or LNIS, is the mutually agreed upon set of standards that define the services that comprise LunaNet and incorporates input from open public dissemination. Establishing these international interoperability standards facilitates a more distributed approach to building up critical lunar infrastructure, allowing various service providers to deliver specific services, coverage and capabilities as demand grows. The goal is to enable any potential LunaNet Service Providers (LNSP) to implement selected services as defined in the LNIS and achieve seamless integration with the greater LunaNet ecosystem. Among the first service providers to instantiate LunaNet will be NASA’s Lunar Communications Relay and Navigation Systems (LCRNS), ESA’s Moonlight Lunar Communication and Navigation System (LCNS), and Japan’s Lunar Navigation Satellite System (LNSS). This article is associated with the upcoming release of LNIS version 5, specifically regarding the accompanying Applicable Document #1 Volume A.

A key component of LunaNet defined in the LNIS is the Lunar Augmented Navigation Service (LANS), which is designed to provide a S-Band Radionavigation Satellite Service (RNSS) via the Augmented Forward Signal (AFS), following some basic principles of GNSS services on Earth. An individual LNSP with multiple nodes can sufficiently deliver services for a mission. However, in contrast to Earth’s GNSS, LANS as a unified service aims to improve individual capabilities by integrating LNSP asset sources from multiple parties (Figure 1). The AFS is a forward link from the perspective of the LNSP node, being broadcast to any number of users in the lunar service volume. It is “augmented” with features distinguishing it from other communications and navigation signals by offering information beyond typical PNT broadcast systems.
Figure 2 describes the range of LunaNet PNT offerings, of which the AFS is a core capability. In addition to PNT services, the AFS provides an avenue to broadcast other information such as network access and scheduling notices for upcoming point-to-point (P2P) contacts, representing an entry point to the LNSP network.

In establishing the AFS standard, several design factors unique to operation in the lunar regime must be considered. These include accommodating varying orbit types, reduced size, weight and power (SWaP) for Moon-orbiting assets, resilience to interference and multipath, and flexibility of implementation to allow LNSPs to provide custom message formats. This article describes the design of AFS, its features, and the benefits it will provide to lunar users. It also discusses the specific challenges and constraints that influenced the design process to complete version 5 of the standard [1].
Background
Following recommendation SFCG REC 32-2R5 [2] from the Space Frequency Coordination Group (SFCG), LunaNet established the AFS to be broadcast with a center frequency of 2492.028 MHz derived from 2436 times 1.023 MHz, a frequency common to legacy GNSS systems. Alternative frequencies that are multiples of 1.023 MHz offer less available two-sided spectrum. The recommendation considers ITU-R RA.479-5 [3], which establishes protection of frequencies for radioastronomical measurements in the shielded zone of the Moon. The adopted frequency band (2483.5 MHz–2500.0 MHz) avoids interfering with the multiple weak L-band GNSS signals received from Earth orbiting satellites, which may also be exploited for cislunar PNT.

Despite these precautions, the frequency choice poses challenges regarding interference with neighboring wireless and 3rd Generation Partnership Project (3GPP) channels also envisioned for use in the lunar environment (Figure 3).
To achieve LANS interoperability, LunaNet specifications must consider the challenges associated with different contributing networks operating in the lunar regime. This involves various orbital designs, with an LNSP possibly using Elliptical Frozen Lunar Orbits to enhance services at the lunar South Pole, while others might opt for circular orbits. Unlike Earth GNSS, this leads to a significant dynamic range of received power on the ground, affecting co-channel interference. Additionally, establishing a common lunar time and reference systems is essential for effective interoperability.
Radio navigation systems rely on accurate, precise and continuous time as a reference source for their transmitted signals and messages. GNSS in orbit around Earth act as sources of the Coordinated Universal Time (UTC) timescale reference to Earth’s surface of equipotential, the geoid. Even though each system may include an identified offset to UTC, they have consistent clock rates as a fundamental aspect for interoperability. LNSPs providing LANS will disseminate LunaNet Reference time (LRT), which serves as a reference for the AFS signal. LRT will be linked to the proposed Coordinated Lunar Time (LTC) that is referenced to the lunar geoid [4]. The link between LRT and LCT will be defined in future versions of the LunaNet interoperability specification.

AFS Overview
The AFS has features similar to the original GPS signal structure, having a low-rate, I channel spreading code in phase quadrature with a higher-rate Q channel spreading code.
where
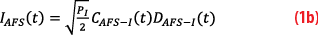
and
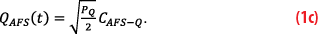
DAFS-I is the I channel data symbol sequence, PI and PQ are the received power levels for I and Q channels, each assumed to be -163 dBW.
Like the original GPS C/A code, the in-phase (I channel) AFS spreading code, CAFS-I, is a 1.023 Mcps binary phase shift keying (BPSK) modulated code, denoted by BPSK(1). The 1.023 Mcps spreading code was chosen for ease of acquisition and to enable low-SWaP and low-complexity receivers. In general, BPSK spreading signals with greater heritage were chosen over Binary Offset Carrier (BOC) signals due to their lower complexity and greater robustness to interference for a given occupied bandwidth. The 500 sym/s AFS data rate and 6000 symbol message block size enable rapid transmission of Clock and Ephemeris data (CED) and provide margin for additional data contents, beyond what is required for PNT.
The quadrature phase (Q channel) signal uses a 5.115 Mcps spreading code, CAFS-Q, denoted by BPSK(5), which is limited in chip rate due to the available ~ 16 MHz bandwidth. Similar to the I channel, BPSK modulation was selected for the Q channel to minimize adjacent-band interference and maintain low receiver complexity.

AFS Data Channel
The AFS data channel consists of a symbol stream that commences with a 68-symbol word that provides high reliability frame synchronization for low SWaP receivers that only use the I channel. This is followed by four subframe blocks (SBs) including SB1, containing the time of interval (TOI) and frame identifier (FID). SB2 contains the CED, while SB3 and SB4 will include almanac data, alerts, network access information, other message types and optional information that can be implemented by service providers.
AFS Data Frame Structure
The AFS data frame design entailed several competing objectives:
• Exploit high performance Low Density Parity Check (LDPC) forward error control (FEC) coding from available standards.
• Provide a frame identifier field independent of the LDPC coding and interleaving to permit changes to the data structure in the future, if needed (e.g., separate interleaving of SB2 and SB3+SB4 messages, or support of a different frame structure).
• Provide a high reliability synchronization word to enable frame sync for low SWaP users at or below the level of the LDPC code.
• Provide a data rate and frame size that permit frequent navigation message updates and flexibility to transmit network status and alert messages.
• Select message and synchronization word sizes that provide useful interleaver factorizations.
To simultaneously achieve all these objectives, several design iterations were conducted in parallel. Iterations involved changes in synchronization word size, SB2-SB4 message lengths, encoding and interleaving, SB1 bit allocations and encoding, with some of this work described in [5].
The resulting frame structure baselined for initial operation is represented by FID=0 and shown in Figure 4. The 68-bit synchronization word was selected to achieve reliable detection at C/N0 = 25.2 dB, for a detection probability of 99% and a false alarm rate of 10-6 per hypothesis, which is below the data message threshold. While carrier tracking performance is limited to C/N0≥25.2 dB for user receivers that only process the I channel, higher reliability frame sync may be achieved by tracking the Q channel pilot.
The rate (52, 9) extended BCH code used in GPS L1C was selected for use in AFS because it has a sufficiently low Message Error Rate (MER) at much lower C/N0 levels than AFS’s LDPC code[5,6]. This selection permits detection of CED at lower C/N0 levels [5]. To support reliable FID decoding, the BCH(52,9) code is re-purposed to provide both a 7-bit TOI and 2-bit FID that are independent from the remaining data.
The AFS TOI increments with every 12-second transmitted frame until it reaches a value of 100, representing a block interval (BI) of 20 minutes, and then resets to zero. The curve fit interval over which the CED is valid is expected to be uniquely defined for each service provider. This approach is analogous to the one in L1C’s CNAV 2 message [6] and is described in [7]. When the curve fit interval is a multiple of the 20-minute BI, and the SB2 CED data stays constant and repeat over several subsequent frames, CED can combine across frames to enhance decoding sensitivity when using a linear block FEC like LDPC. This intermediate step takes the soft decisions of multiple codewords and adds them symbol-wise to produce a final set of values (Figure 5). Figure 6 shows that with just two combined messages of SB2, the receiver can read data at 3 dB lower C/N0, at a performance close to SB1.

To exploit commercially available standards and provide a flexible encoding scheme for varying frame sizes and rates, a set of rate-½ LDPC FEC codes were constructed using the 5G NR technical specification for SB2-SB4, which consists of 5,880 interleaved FEC coded symbols [5,8]. The raw, CRC-protected NAV information bits contained in SB2-SB4 are separately encoded and then interleaved together. Flexibility to support different LNSPs for future accommodations can be obtained through a combination of lifting and puncturing on the protograph structure [8].
The performance of these codes is shown to surpass all other currently used GNSS codes in terms of bit error rate performance vs Eb/N0 (Figure 7). If needed for other FIDs, the documented 5G NR design process can be repeated to achieve a unified AFS approach using accessible standards [8].
A navigation user is primarily interested in the likelihood of successfully demodulating CED. This quantity may be computed from Ps1=1-PM, where PM is the MER. In this case, a message is successfully decoded when all bits in the message are correct and so PM=0.01 corresponds to the case when at least one bit is incorrect in one out of 100 messages.
For signals that use block encoding of CED using a single message, a reasonable message error rate of 10-2 allows for a success rate of 99%. For legacy signals requiring multiple independent messages to decode CED, the success rate is determined as the product of the success rates needed for each message. For example, with L5 and C/A code signals, three messages are needed for CED. Under the assumption the noise induced errors in each message are independent,
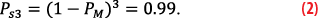
For a 99% success rate, such signals require that PM=1-0.991⁄3=0.0033. Similarly, the probability of successfully decoding N messages is given by

As described in [10], one typically requires a receiver to acquire and obtain a fix with a 95% confidence interval. Let P4Acq be the probability of acquiring four satellites needed for a fix. The probability of acquiring four satellites needed for a fix (assuming independent measurements from four satellites), and successfully demodulating CED using N messages for each of four satellites with a joint 95% confidence is given by
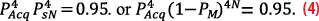
If we assume acquisition and data decoding are designed to have the same reliability, PAcq=PsN, the MER required for 95 % confidence is given by

This can be solved for the required MER, resulting in PM=1-.
The MER for a message of size M bits may also be determined from the Bit Error Rate (BER) by PM=1-(1-Pb)M≅MPb, where 1-Pb is the probability that a bit is correct. Therefore, (1-Pb )M is the probability that all bits in a message are correct, assuming data bits errors are independent and random. Solving for Pb and combining the equations above results in
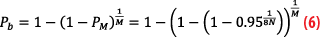
or to a good approximation,
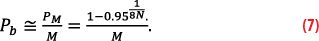
The 95% confidence metric provides a fairer comparison of the data demodulation performance than using a fixed BER or MER criterion or fixing the data message block length to compare different data modulation and encoding approaches as described in [9]. The required BERs and MERs for a TTFF with 95% confidence are given in Table 1 for GPS, Galileo and AFS.


The resulting error rates are very close to the previously used criterion of BER = 1×10-5 for GPS and MER = 1% assumed in previous works [6].
As observed, even though the AFS message size is the largest of any in satellite navigation signals, it can be detected at lower Eb/N0 than any previous GNSS message. Its threshold C/N0 is 1 dB lower than in GPS L1 C/A and is comparable to Galileo E1B (E1OS), even with higher data rate. Due to the possibility of CED combining two short (12 second) messages (3 dB improvement), AFS can enable data demodulation at 4 dB lower C/N0 levels than the C/A code signal and 3 dB lower C/N0 than the Galileo E1B signal.
To mitigate fading, a classical block interleaver was implemented across encoded subframes 2, 3 and 4. The block interleaver can be visualized as a two-dimensional array with 60 rows and 98 columns. The usage of interleaving allows the noise to be distributed across all the LDPC encoded subframes, improving the individual decoding process for each subframe as described in [11].

Spreading Signals and Ranging Codes
As with terrestrial GNSS signals, the impacts of multiple access interference need to be limited. Therefore, the I channel AFS spreading code was selected to use a BPSK(1) spreading code with improved cross-correlation properties relative to C/A code by using a longer spreading code. Because of its narrower bandwidth, the I channel is most susceptible to co-channel interference, but is spectrally separated from the wireless and 3GPP bands, providing improved adjacent band interference rejection, as shown in Figure 3.
The combined I and Q channel ranging code structure is shown in Figure 8.
I Channel Spreading Code
The I channel spreading code period matches the data symbol period and employs a 2 ms long, 2,046-chip short cycled 2,047-length Gold code. This provides immediate bit synchronization and results in an acquisition implementation that is only a factor of 2 more complex than the C/A code. As in GPS, 210 spreading codes were selected based on the best auto-and cross-correlation properties from the set of 211+1=2048 possible Gold codes.
The AFS Gold codes are designed from the preferred pair of maximal length sequences based on the following generator polynomials [8],
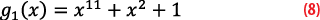
and
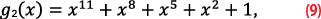
where the polynomials are initialized to 11111111111 and codes are selected in a manner analogous to the C/A code generation described in ICD-GPS-200.

Table 2 compares the use of a 1023-chip C/A code for the AFS-I channel vs the selected 2046-chip Gold code. For a 1023 chip C/A code, cross-correlation is assumed to be over 1 ms during acquisition and 2 ms during track, due to the ambiguity between data symbols and spreading code prior to synchronization. The cross-correlation for the 2,046-chip AFS Gold code is always over 2 ms because the data symbols are aligned with the code period. The cross-correlation results assume an equal probability of even and odd cross-correlations for the LDPC coded and interleaved AFS data symbols between satellites. The results assume an equal probability of even and odd cross-correlations because the data symbols between satellites are approximately uncorrelated.
A 2046 chip AFS I channel spreading code was found to provide a 3 dB improvement 99.9% of the time during acquisition, compared to the GPS L1 C/A spreading code and over 1 dB while tracking, assuming random data symbols. A 2046-chip short cycled 2053-length Weil sequence was found to have comparable performance, but a Gold code was selected to simplify implementation.
The improvement over C/A code is 1.6 dB for acquisition and 2 dB during track with a 2 ms coherent integration. For this reason, the longer 2046 AFS Gold code was selected instead of the 1023-chip C/A code.

Q Channel Spreading and Overlay Codes
The Q channel pilot signal leverages the 10230-chip L1C primary spreading code, for which 210 codes had already been designed. Fifty E5b sequences were initially analyzed in this three-tiered structure (Figure 8), and L1C codes were selected due to their superior cross-correlation performance and pre-existence of 210 spreading codes ready for use, pending formal confirmation for AFS use.
A secondary code from the Galileo E5b-I signal (HEX letter “E” or 1110 in binary) was leveraged to produce a tiered intermediate code, CInt, of length 8 ms consisting of the modulo-2 sum of a repeating four chip secondary code and a 2-ms 10230-chip repeating primary code.
Initial correlation results assumed the same secondary spreading code for all satellites, but it was found that by performing three circular shifts of the 1110 secondary overlay, the overall code correlation properties of the tiered codes were dramatically improved. The circularly shifted codes shown in Table 3
are perfectly orthogonal, making this set of codes optimal for a length-4 overlay sequence.
As described in [5] and [12], the acquisition search complexity of a repeating code scales roughly with the product of the chip rate and the code length.
State of the art acquisition circuitry today can search the 10230-chip, 10.23 Mchip/s L5 code directly [12]. The AFS pilot primary code is roughly ½ the complexity of an L5 acquisition search implementation, with comparable processing gain. The tiered intermediate code with 40,920 chips can be searched with an acquisition engine having twice the complexity of L5 only receivers, though resulting in a processing gain (proportional to coherent integration period × chip rate) that is 6 dB greater. The AFS’s multi-tiered acquisition structure therefore provides exceptional receiver acquisition sensitivity in interference environments, while also providing a tertiary code for absolute time.

The Tertiary Overlay Code
This family of AFS spreading codes is based on Weil sequences [13]. The AFS tertiary overlay sequences are derived from the length-1499 Legendre sequence, which is generated by the quadratic residue approach from [14] but may also be generated in a recursive manner [15]. In the Legendre sequence,
L=(L0,L1,…,L1498) element values are

Element LSn is always -1, and
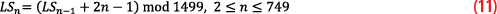
where LS1=1. The set of 749, length-1499 Weil sequences is then obtained as
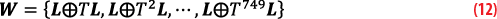
where the Tk operator represents the cyclic shift of the sequence for k places, and ⊕ is the modulo-2 operation. Each Weil sequence is a component-wise exclusive-OR of the Legendre sequence and its circular shift. The value of the shift is the index of Weil sequences, which are also of length-1499. The length-1500 set of augmented Weil sequences is obtained by appending -1 to each sequence in the set W. A search was conducted to produce 210 Weil-based overlay codes with the best autocorrelation properties (lowest sidelobes) and low mutual cross-correlations, using minimum RMS cross-correlation (sidelobe) values as the criterion.
The code also serves as a source of absolute time for receivers with knowledge of time to within 12 seconds. Synchronization to the tertiary code normally occurs after acquisition and tracking of the AFS intermediate code CInt. The tertiary code phase is determined by performing a maximum likelihood search by dwelling over some number of tertiary code symbols for each possible code phase offset. Figure 9 shows the 99% C/N0 threshold as a function of dwell period. A minimum of 22 symbols must be integrated to achieve synchronization performance comparable to the I channel synchronization word threshold (25.2 dB-Hz). Up to 50 symbols are needed to achieve C/N0 performance that is well below the data threshold. Absolute time synchronization to within one AFS-Q chip may be determined by correlating 50 successive 8-ms symbols against 1500 possible CInt code-phase offsets, which takes less than one second in software.

Tiered AFS-Q Code Performance
An initial assessment of the tiered code performance is shown in Table 4 for sets of primary, secondary and tertiary sequences that were sequentially paired with each other. Results are shown for the L1C primary code sequences versus the Galileo E5b primary code sequences under different coherent integration assumptions, corresponding to acquisition of the 2-ms sequence, acquisition of the tiered 8-ms secondary sequence, or tracking with 100-ms or 200-ms coherent integration periods considering synchronization to the tertiary code sequence.
Even though there is a larger set of L1C spreading codes, 99% and 99.9% cross-correlation results with 210 length-1500 tertiary chip Weil sequences, four secondary overlay codes and 210 L1C primary codes are 0.3-1 dB better (blue boxes) than previous results with 50 E5b primary sequences, four secondary sequences and fifty 1500-chip tertiary overlay codes. For these reasons and the existence of the larger code set, the L1C Weil sequence was selected for use in the AFS. No effort was made to optimize specific sets of tertiary, secondary and primary tiered codes. Example code sets are provided within the first release of LNIS Applicable Document 1 Volume A, for use by service providers during the initial development [11].
Conclusions
The AFS was designed to deliver high-performance PNT services and low-rate data messages to users in the lunar vicinity, while accommodating a range of use cases and operational modes.
The AFS-I channel design enables low SWaP implementations, analogous to C/A code receivers, while providing high performance LDPC coding and frame synchronization without an overlay sequence. This is achieved by using a robust 68-symbol synchronization word on the I channel that enables frame sync near the C/N0 detection threshold of the 5G NR-based LDPC FEC.
The AFS-I channel also employs a 1.023 Mcps, spreading code chips about twice the complexity of the GPS C/A code. To accommodate increased data throughput, however, the symbol rate for messages is increased tenfold compared to GPS C/A. Given the increased data rate, a high performance 5G NR LDPC FEC enables robust data decoding that exceeds the E1OS and C/A code.
The AFS-Q channel design establishes a pilot channel for use in precision tracking. It features a chip rate of 5.115 Mcps using a BPSK modulation to make use of the available bandwidth, reduce adjacent band interference and avoid complexities involved with BOC signals. A tiered code approach is employed to facilitate flexibility in receiver acquisition, data synchronization, absolute time synchronization and precision signal tracking. Overall, the AFS provides the following enhancements:
• Employs 5G NR Forward Error Control coding with the best decoding performance of any GNSS signal;
• Multi-tiered ranging codes permit receivers to trade acquisition sensitivity with complexity;
• Tertiary overlay code enables rapid time dissemination, high integrity code acquisition, frame synchronization and a special messaging capability;
• High integrity sync word enables low SWaP single channel users to perform frame sync at levels commensurate with the demodulation of the LDPC coded data channel without a pilot overlay;
• The signal structure supports future changes through the robust BCH encoding of the FID field.
Acknowledgements
A portion of this work was funded by the NASA Lunar Communications Relay and Navigation Systems (LCRNS) project to inform the LunaNet Interoperability Specifications, with Aerospace funded under contract 80GSFC19D0011.
References
(1) LunaNet Signal-In-Space Recommended Standard—Augmented Forward Signal (LSIS), Draft Version 5, August 31, 2023.
(2) Space Frequency Coordination Group (SFCG), “Communication and Positioning, Navigation, and Timing Frequency Allocations and Sharing in the Lunar Region,” Recommendation SFCG 32-2R5, 7 June 2023.
(3) International Telecommunication Union—Radiocommunication, “Protection of frequencies for radioastronomical measurements in the shielded zone of the Moon,” Recommendation ITU-R RA.479-5, May 2003.
(4) Ashby, N., Patla, B.,“A Relativistic Framework to Estimate Clock Rates on the Moon,” The Astronomical Journal, Vol 168, No 3, August 2024. https://dx.doi.org/10.3847/1538-3881/ad643a.
(5) P.A. Dafesh, G. K. Khadge, N.S. Wong, G. Djuknic, (2024), “Flexible Data and Frame Synchronization Structure for the LunaNet PNT Signal,” Proceedings of the ION 2024 Pacific PNT Meeting (pp. 844–866).
(6) J.W. Betz, M.A. Blanco, C.R. Cahn, P.A. Dafesh, et al., “Description of the L1C Signal,” ION International Technical Meeting of the Satellite Division, Sept. 2006, p. 2080.
(7) LunaNet Signal-In-Space Recommended Standard (LNIS)—Augmented Forward Signal (Noted as Applicable Document 1 [AD1 Vol-A] in LNIS V5, August 2024.
(8) 3rd Generation Partnership Project; Technical Specification Group Radio Access Network; NR; Multiplexing and Channel Coding, Release 16, V16.2.0, 3GPP Standard TS 38.212, Jul. 2020.
(9) M. Anghileri, M. Paonni, et al., “Assessing GNSS Data message performance,” Inside GNSS, March-April 2013.
(10) RTCA DO-229F, “Minimum Operational Performance Standards (MOPS) for Global Positioning System /Satellite Based Augmentation System Airborne Equipment,” June 2020.
(11) P. A. Dafesh, E. L. Vallés, J. Hsu, D. J. Sklar, L. F. Zapanta, C. R. Cahn, “Data Message Performance for the FutureL1C GPS Signal,” Proceedings of the ION International Technical Meeting, 2007.
(12) Greg Turetzky, “L5-only receiver designed for mobile phones,” GPS World, October 5, 2020, https://www.gpsworld.com/l5-only-receiver-designed-for-mobile-phones/.
(13) J.J. Rushanan, “The Spreading and Overlay Codes for the L1C Signal,” Navigation, Vol. 5, No. 1, Spring 2007.
(14) G.H. Hardy and E.M. Wright, An Introduction to the Theory of Numbers, 5th ed., Clarendon Press, Oxford 1979, pp. 67-71.
(15) K.V. Rao and V.U. Reddy, “Biphase Sequence Generation with Low Sidelobe Autocorrelation Function,” IEEE Tran. Aerospace & Electronics Systems, Vol. AE-22, No. 2, Mar 1986, pp. 128-133.
Authors
Dr. Philip A. Dafesh
is a Distinguished Engineer at the Aerospace Corporation. He supports the development of GPS and space systems and has contributed to the development of the modernized GPS signal structure and associated receiver processing for GPS L1, L2C and M-Code signals. Phil hold B.S. degrees in electrical engineering and physics form Cal Poly Pomona and received his Ph.D. degree in electrical engineering from UCLA. He has published 64 technical papers and holds 21 patents involving GNSS modulation, signal combining, interference mitigation and related technologies.
Gourav K. Khadge
is a senior member of technical staff in the Digital Communication Implementation Department of The Aerospace Corporation. He received his M.S. in electrical engineering in 2018 from the University of California, Los Angeles, specializing in signals and systems. His current work is in research, analysis, testing, and development in wireless communications signals and systems, software defined radio, GPS and GNSS technologies. He has published four papers in IEEE, ION and The International Symposium on Information Theory and holds one patent in GNSS receiver signal processing technology.
Nathan S. Wong is a senior member of technical staff in the Digital Communication Implementation Department at the Aerospace Corporation, specializing in software-defined radios and communication waveform design and validation. Previous work of his includes circuit design, machine learning and system integration for aviation platforms. He received his M.S. in electrical engineering in 2018 from the University of California, Los Angeles, with a research focus on information theory, error correction and channel modeling. He has published two technical papers.
Dr. Goran Djuknic is a member of the Performance & Analysis group at the Aerospace Corporation, specializing in wireless communications, digital signal processing, analytical methods and navigation signal design. His contributions to GNSS included jamming mitigation algorithms, snapshot positioning, and GPS signal generation. At Raytheon Technologies, he developed methods for wireless communication in airline cabins, cargo spaces and jet engines. He researched and developed methods for modeling, simulation and measurement of signal propagation in airliner cabins and elevator shafts. He has published 10 technical papers and was awarded 14 patents.
Juan Crenshaw has been a navigation engineer at NASA’s Goddard Space Flight Center since 2020. He has over 15 years of prior experience with communications networks and spacecraft navigation, holding telecommunications engineering degrees from UPM and UAX (Spain). Juan is involved in technology development for lunar position, navigation and timing and is dedicated to promoting interoperable solutions, including the development of standards such as LunaNet. Additionally, Juan is involved in international organizations, including the International Committee on GNSS (ICG), Interagency Advisory Group (IOAG), and the Consultative Committee for Space Data Systems (CCSDS).
Cheryl Gramling has over 40 years of experience leading trajectory design and navigation for NASA missions in LEO, GEO, HEO, lunar, and libration points, including relay systems and distributed system missions such as the Magnetospheric Multiscale. With expertise in NASA Communication Networks, PNT systems and operations, her focal areas are ground-based and autonomous orbit estimation, extrapolating existing capabilities in the networks and onboard sensors to cost-effectively achieve mission objectives. She now serves as the Lunar PNT and Standards Lead and is a Goddard Senior Fellow.
Brian C. Peters is pursuing his Ph.D. in electrical engineering and computer science at Ohio University within the Avionics Engineering Center. His research interests include GNSS interoperability, GNSS interference monitoring, weak-signal GNSS, pulsar-based navigation/timing, and lunar navigation systems. He has previously worked on Ohio University’s Bobcat-1 CubeSat mission, and he was a navigation systems engineer for NASA’s CAPSTONE mission. He is currently a Pathways intern at NASA Goddard Space Flight Center where he supports the LCRNS project.
Floor Thomas Melman received his MSc in Aerospace Engineering at the Delft University of Technology in 2018. He is currently a radio navigation engineer in the radio navigation systems and techniques section within ESA/ESTEC in the Netherlands. He is coordinating the GNSS receiver experiment that will fly on the Lunar Pathfinder mission and supports the ESA Moonlight program that will provide lunar communication and navigation services. Furthermore, he is the ESA lead within the LunaNet PNT working group that will define standards and protocols enabling interoperable lunar PNT systems.
Richard Swinden is a navigation system engineer in the RF Systems Division at the European Space Agency. His main current responsibilities involve providing system and navigation engineering support to lunar and Mars-related projects including Moonlight, Argonaut and LightShip-MARCONI. He holds a first-class Master of Electronic Engineering degree from the University of Nottingham and has more than 15 years of experience in the GNSS and space domains.
Cosimo Stallo received a Ph.D. in Microelectronics and Telecommunications at the University of Rome Tor Vergata. He has experienced several years working on GNSS with University of Tor Vergata, RadioLabs, Italian Space Agency as senior researcher and technical manager of ESA and EUSPA projects. He joined Thales Alenia Space Italy in December 2019 as senior system navigation engineer. In 2023, he was appointed head of unit on E2E system design within the Navigation Systems Department, Domain of Observation and Navigation Italy. In June 2024 he joined ESA as LCNS/moonlight principal navigation system.
Masaya Murata joined the Japan Aerospace Exploration Agency (JAXA) in 2017 and is the lunar PNT lead for Japan lunar PNT system called Lunar Navigation Satellite System (LNSS). He had 10 years of private-company experience before joining JAXA and earned his Ph.D. from the University of Tokyo in 2017. From October 2021 to September 2022, he served as a visiting scholar at the Aalto university in Finland and the University of Texas at Austin, respectively. He is now actively participating in the International Committee on GNSS (ICG) and the Interagency Operations Advisory Group (IOAG) to facilitate the international collaboration for lunar PNT.






