With a Low-cost Single-frequency Multi-GNSS Receiver
Although precise point positioning (PPP) has been largely limited to applications in open environments using high-end GNSS receivers, recent test results demonstrate that a new PPP system with a mass-market receiver can significantly improve positioning accuracy in urban environments.
ZHITAO LIU and YANG GAO, The University of Calgary
Precise positioning for mass-market applications faces several challenges. Among them, only low-cost GNSS receivers in the form of small size modules and chips are widely employed in those applications. These suffer large noise levels in pseudorange and more frequent cycle slips in carrier-phase observations, compared to high-end GNSS receivers. Additionally, mass-market applications are often conducted in challenging signal environments with severe navigation signal blockage and attenuation. Finally, current precise point positioning (PPP) algorithms are designed mainly for high-end GNSS receivers.
PPP requires state space representation (SSR) corrections to mitigate satellite orbit, clock and other sources of errors and effects in GNSS measurements. These SSR corrections are freely available from many scientific organizations such as the International GNSS Service (IGS) and from commercial suppliers, such as RTX from Trimble and TerraStar-X from Hexagon, via satellite link or Internet connection. Driven by emerging mass-market applications that demand precise location information, new correction services are being developed such as the TruePoint.io GNSS assistance data from RX Networks, the Skylark correction service from Swift and the SAPA correction service from Sapcorda. Although high accuracy has been widely demonstrated with PPP techniques, it is still largely limited to applications in open environments and using high-end GNSS receivers.
Multipath effects and non-line-of-sight (NLOS) signals constitute two major obstacles to using GNSS in urban environments, with errors up to hundreds of meters. Various methods have been developed to improve positioning accuracy in urban environments, including integrating low-cost GNSS receivers with multi-sensors (e.g. inertial measurement unit (IMU), visual odometry (VO), WiFi, and Bluetooth), and 3D map-aided (3DMA) GNSS positioning methods.
A GNSS-only approach is cost-effective due to no additional sensors required and has been widely investigated, for example, a dual-polarized antenna, a consistency check using receiver autonomous integrity monitoring (RAIM) algorithms, and machine-learning methods such as support vector machine (SVM) and deep learning. Each has their own advantages and disadvantages.
Here we focus on a new PPP system based on a low-cost single-frequency GNSS receiver. A machine learning based method for NLOS signal detection is first described. With detected NLOS information, a new weight scheme is then applied to mitigate NLOS errors in carrier-phase, phase rate and pseudorange observations in urban environments. With the NLOS effect mitigated, a two-filters algorithm is designed for measurement processing to improve positioning accuracy and reliability. Positioning results from two land-vehicle kinematic tests indicate that significant positioning accuracy improvement can be achieved in urban environments using this system.
Methodology
The new PPP system includes three major components:
• an SVM-based classifier to detect NLOS observations and output their probabilities.
• a weight scheme to map the NLOS probabilities into GNSS observation variances for application by the GNSS estimator.
• a two-filters approach for GNSS observation processing and position determination in urban environments.
NLOS Detection wih SVM Classifier
Accurately detecting and properly handling NLOS observations are critical for improving positioning accuracy in urban environments. Here we apply the SVM to detecte the NLOS observations. The SVM is a canonical classifier that has been widely applied in many fields. It is not only computationally efficient but also able to utilize non-linear margin to classify multi-dimensional features when equipped with the radial basis function (RBF) kernel. Our new PPP system uses an RBF SVM classifier, which includes six features calculated from the GNSS observations to predict the probabilities of GNSS observations as LOS or NLOS signals, namely PLOS or PNLOS in the following. The six features include the C/N0, the single-difference ambiguity, the double time-differenced phase, the double time-differenced pseudorange, the phase and pseudorange consistency calculated from the discrepancy between the phase rate predicted measurement and the observed measurement. More details can be found in our article “An SVM Based Weight Scheme for Improving Kinematic GNSS Positioning Accuracy with Low-Cost GNSS Receiver in Urban Environments,” in Sensors magazine, December 2020.
INLOS Probability-Based Weight Scheme
When NLOS observations are detected, the predicted NLOS probability from the output of the SVM classifier can be a good indicator of the magnitude of observations being affected by multipath and NLOS signals. It can therefore be used to create an effctive weight scheme to mitigate the impact of the multipath and NLOS signals. This weight scheme maps the NLOS probability into the observation variance, which consists of a LOS component and a NLOS component, and it can be written as:

where Cdj, CPj and CLj represent the variance for GNSS phase rate, pseudorange and phase observations for satellite j, respectively. σd,l denotes the LOS part standard deviation of phase rate observation (0.06m/s in this work). b is a constant empirical value to be tuned. e is the Euler’s number, e≈2.718. PNLOS is the NLOS probability from the SVM classifier. The maximum value of PNLOS is set to equal 0.95 to avoid astronomical variance values which will corrupt the 64-bits float-data width-based estimator. a is a constant empirical value to be tuned; ele is the elevation angle in rad. d is the scale factor for phase and pseudorange LOS observation variance (0.01 for phase and 1 for pseudorange in this work). c is a constant empirical variable to be tuned and will have different values for pseudorange and phase observations. When the PNLOS is smaller than 0.4, the observation will be considered as LOS signal.

Two-Filter Algorithm
The L1 single-frequency observation equations with multi-constellations for precise point positioning (SFPPP) can be written as:

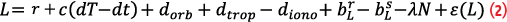
where P and L are the raw GNSS pseudorange and phase observations. r represents the satellite to receiver distance. dT and dt denote the satellite clock and receiver clock biases respectively, and they are to be estimated individually for different navigation sytems. c is the speed of light in vacuum. dorb, dtrop, diono are the orbital, tropospheric and ionospheric errors respectively. bPr and bPs are the receiver and satellite pseudorange hardware biases. bLr and bLs are the receiver and satellite phase hardware biases. N and λ are the phase ambiguity and the carrier phase wavelength, ε(P) and ε(L) represent observation noise for pseudorange and phase respectively.
The error sources in the observation equations must be corrected or estimated for precise position determination. The orbital error, satellite clock bias and ionospheric delay are to be corrected using the real-time products from the French National Centre for Space Studies (CNES). The zenith wet part and hydrostatic part of the tropospheric error are corrected using the Saastamonion model. The receiver and satellite phase biases bLr and bLs are stable over a short period thus can be absorbed by the ambiguity terms to be estimated along with position coordinate parameters. The code bias bPs is corrected using the 30-days differential code bias (DCB) product from the Center for Orbit Determination in Europe (CODE).
Although the proposed SVM-based weight scheme can significantly mitigate the effect of multipath and NLOS error, concerns still exist in severe signal blockage environments with very poor satellite geometry. To further improve the robustness of the position solution in urban environments, we have adopted a velocity-based kinematic model to constrain the position solution with respect to the estimated velocity information. Traditionally, a single Kalman filter is used to process all available GNSS measurements to simultaneously estimate the receiver position and velocity. This however may suffer from poor robustness in its positioning solutions due to undetected NLOS errors in all observations. In our work, two separate Kalman filters are employed, which include a velocity filter for velocity determination using only phase rate observations and a position filter for position determination using both pseudorange and phase observations. This two-filters approach can provide more reliable velocity solution which can improve the robustness and accuracy of the position filter. The corresponding state vectors for the two Kalman filters are:


where x1 and x2 are the state vector for the velocity filter and the position filter, respectively. v is the velocity vector, is the receiver clock drift; r is the position vector, dtG, dtR and dtE denote receiver clock bias for GPS, GLONASS, Galileo and BeiDou systems, respectively. N represents the phase ambiguity for each satellite. The velocity, receiver clock drift and receiver clock bias states are modeled as a random walk process while the ambiguity term as a random constant process.
The proposed methods and algorithms for SFPPP with multi-constellations and low-cost GNSS receivers have been implemented into the software system P3-SF developed at the University of Calgary. P3-SF can be embedded in a low-cost GNSS receiver as a real-time positioning engine. A consistency check based on a chi-square test between the velocity filter and the position filter is also implemented to ensure the integrity of the positioning system. To further enhance the integrity of the positioning system in the presentation of NLOS/LOS missclassification, a consistency check based on chi-square test is also implemented in the velocity filter and the position filter.
Field Tests and Data Description
To assess the performance of the proposed SFPPP system with a low-cost GNSS receiver in urban environments, we developed a vehicle-based data acqusition system. As shown in Figure 1 on the upper-left, an upward fisheye camera was installed on the vehicle roof to capture the surrounding environments and provide satellite visibility ground truth for the training and testing of the SVM model. A NovAtel SPAN system, as shown in Figure 1 on the lower left, which includes a high-end Novatel Propak6 GNSS receiver and a tactical IMU with a built-in fiber optical gyroscope, is used to provide the position reference solutions (accurate at decimeter-level in urban environments).
A low-cost u-blox M8T single-frequency multi-GNSS receiver and a low-cost u-blox F9P dual-frequency multi-GNSS receiver (sharing the same GNSS signal splitter with the Novatel SPAN system) are used as shown in Figure 1 on the right. Only the GNSS raw observations from the u-blox M8T are used for position determination using P3-SF while the position outputs from the other receiver will be used for performance comparison. A single-board computer (Odroid N2) collects data from all GNSS receivers and the fisheye camera (the time tag of its image frames is properly aligned to the GNSS time).
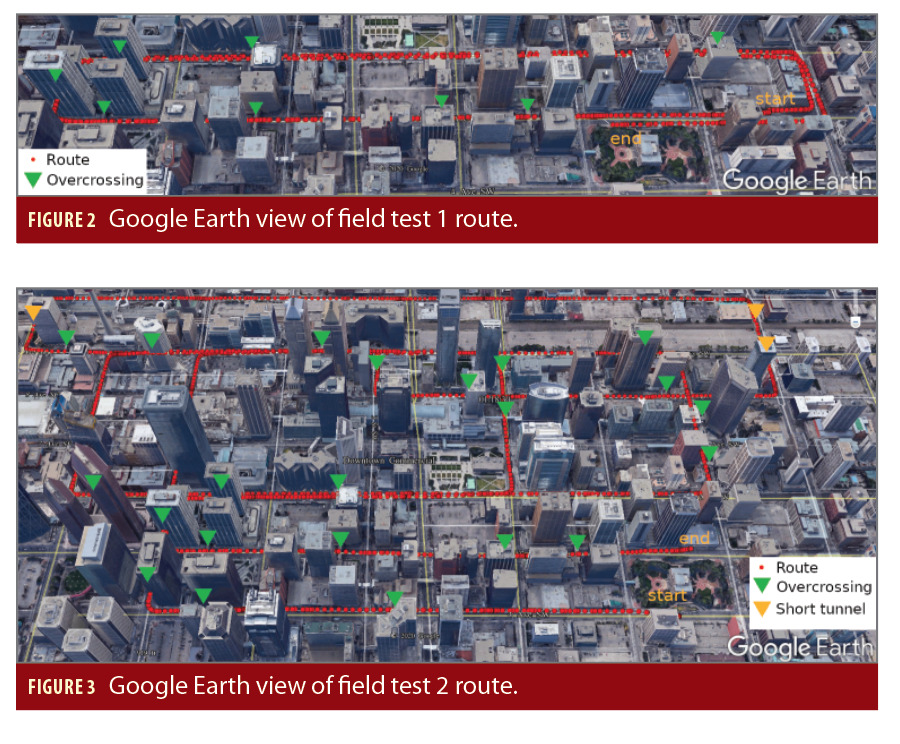
Two kinematic field tests were conducted using the vehicle based data acquisition system in the downtown of Calgary, on August 4 (field test 1) and October 12 (field test 2) 2020. Figures 2 and 3 show the test routes, respectively. In addition to tall buildings on both sides of the streets, there are many short tunnels and pedestrian bridges connecting buildings (see the yellow and green triangles). Severe signal blockages and multipath effects therefore exist along the test routes.
The test vehicle moved at a speed of around 50km/h (the speed limit in urban Calgary) during both field tests. Field test 1 was about 10 minutes long and the dataset was used to train and test the SVM signal classifier. Field test 2 lasted about 30 minutes and the dataset has been used for positioning accuracy evaluation. As to the GNSS data acquisition setups, the u-blox M8T receiver was set to track GPS, GLONASS and Galileo since the maximum number of concurrent constellations that can be observed by the receiver is three. The data sampling rate was 10 Hz and the elevation cutoff angle was set to 5 degrees to allow more satellites available in severe signal blockage environments.
The satellite visibility can be acurrately calculated by comparing the segmented fisheye camera image with its location on it. There are 6078 images captured by the upward fisheye camera in field test 1 which were segmented manually using a labeling tool developed at the University of Calgary to calculate the satellite visibility ground truth for all GNSS observations. 70% of the data was used for training the SVM classifier while the remaining 30% of data was used for positioning performance evaluation. The overall classification accuracy reaches 86.05%. The classification can run in real-time on a low-power device like a Raspberry Pi.
Positioning accuracy and comparison
The performance of the new PPP system was first assessed by comparing it to typical single point positioning (calldd traditional system hereafter) which uses a single filter to process the pseudorange measurements and perform position determination in urban environemnts. For both cases, the real-time product from CNES are applied to mitigate orbital, satellite clock and ionospheric errors and the 30-day DCB product from CODE is used to mitigate code bias. Further, the SVM-based weight scheme is applied to determine the variance of the pseudorange observations in the traditional system and variances of the pseudorange, phase and phase rate observations in the new PPP system. The major difference is that the phase measurements become the principal observable for position determination and two more separate filters are employed in the new PPP system.
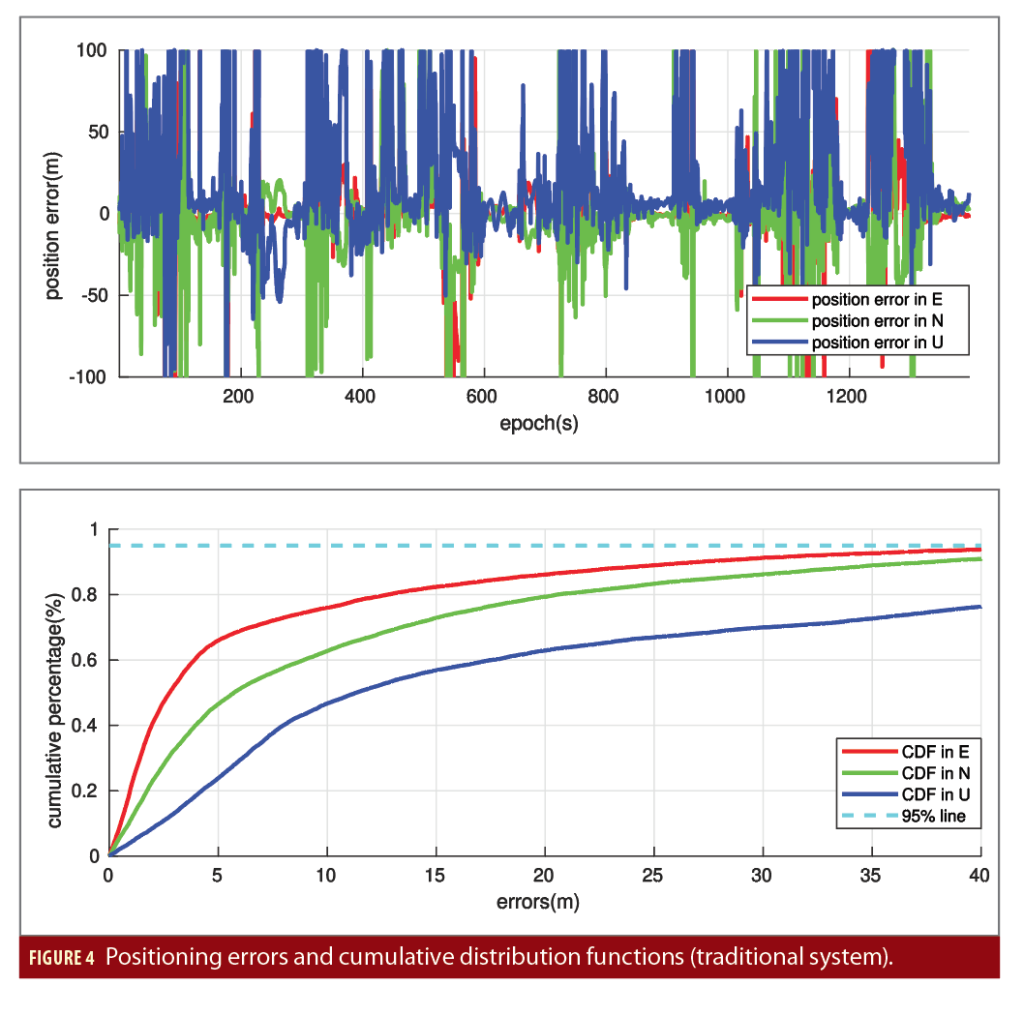
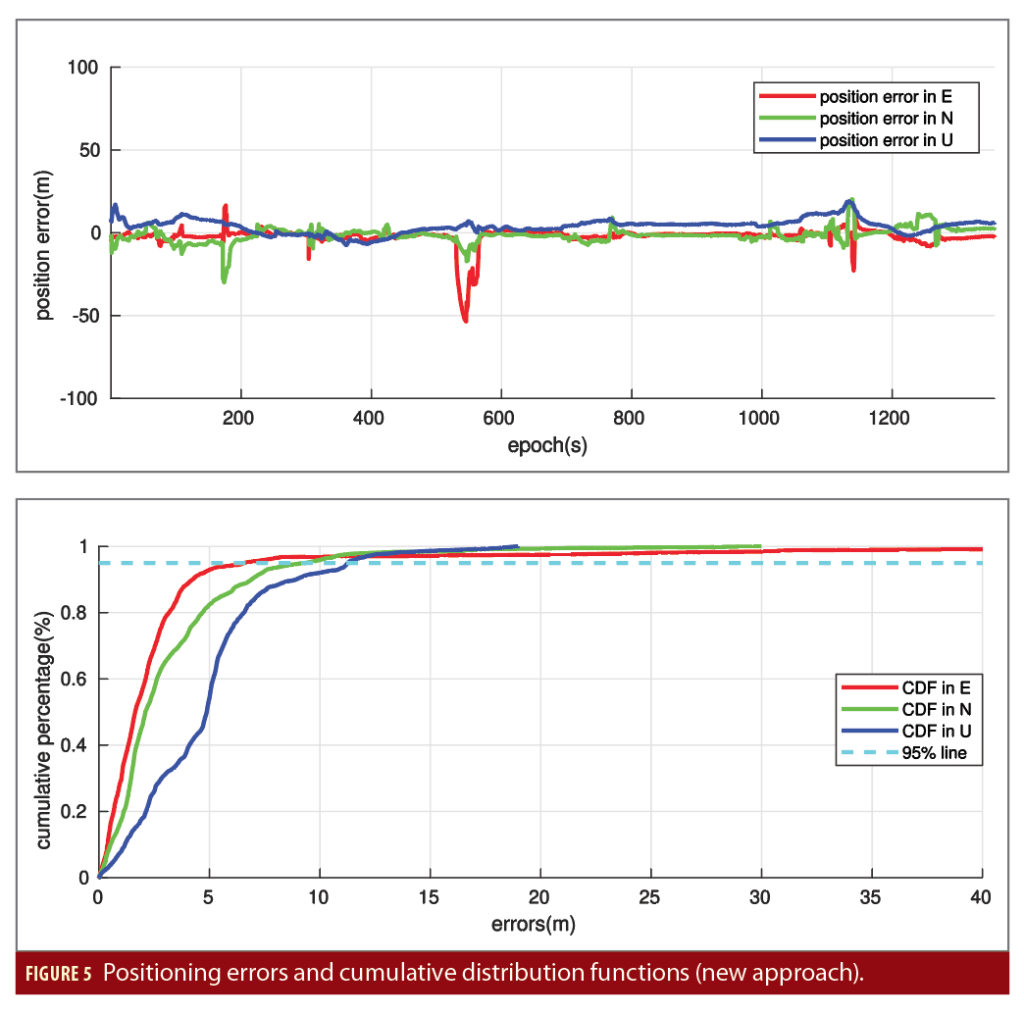
Shown in Figures 4 and 5 are the positioning errors and its cumulative distribution function (CDF) obtained from the traditional system and the new PPP system, respectively, using the data from the low-cost u-blox M8T single-frequency multi-GNSS receiver. The results in Figure 4 indicate very poor positioning solutions due to the effect of significant NLOS observations and poor satellite geometry in urban environments. The horizontal positioning accuracy is 47.9m while the vertical positioning accuracy is 83.7m in terms of root-mean-squares (RMS) errors.
The results in Figure 5 indicate that the new PPP system can significantly reduce the positioning errors in both horizontal and vertical directions. The horizontal positioning accuracy is 7.9m while the vertical positioning accuracy is 5.8m in RMS errors. This corresponds to an improvement of 83.6% and 93.1% over the traditional system in the horizontal and up directions, respectively.
As a comparison, we see that the 95% CDF of the positioning errors using the traditional system exceeds 40 meters in the east, north and up directions, while the new PPP system brings down the 95% CDF to 5m, 10m and 12m in the three coordinate directions. This confirms the importance of phase observations to position determination due to much lower level of observation noises and multipath effects compared to the pseudorange measurements. The robust velocity solution from a separate velocity filter also plays a crucial role for kinematic positioning in urban environments since the phase rate measurements are less affected by the NLOS signals and multipath effects.
In Figure 5, we notice that there are a significant position error spike at the epoch 550s in the east direction and two other smaller position error spikes at the epoch 180s and 1120s in the east and north directions, which can also be observed in all three coordinate locations. This can be due to misclassification by the SVM-based signal classifier as well as poor GNSS signal visibility in environments with severe signal bloackages. An integration with a low-cost IMU could provide more information to enhance the reliability of NLOS detection.
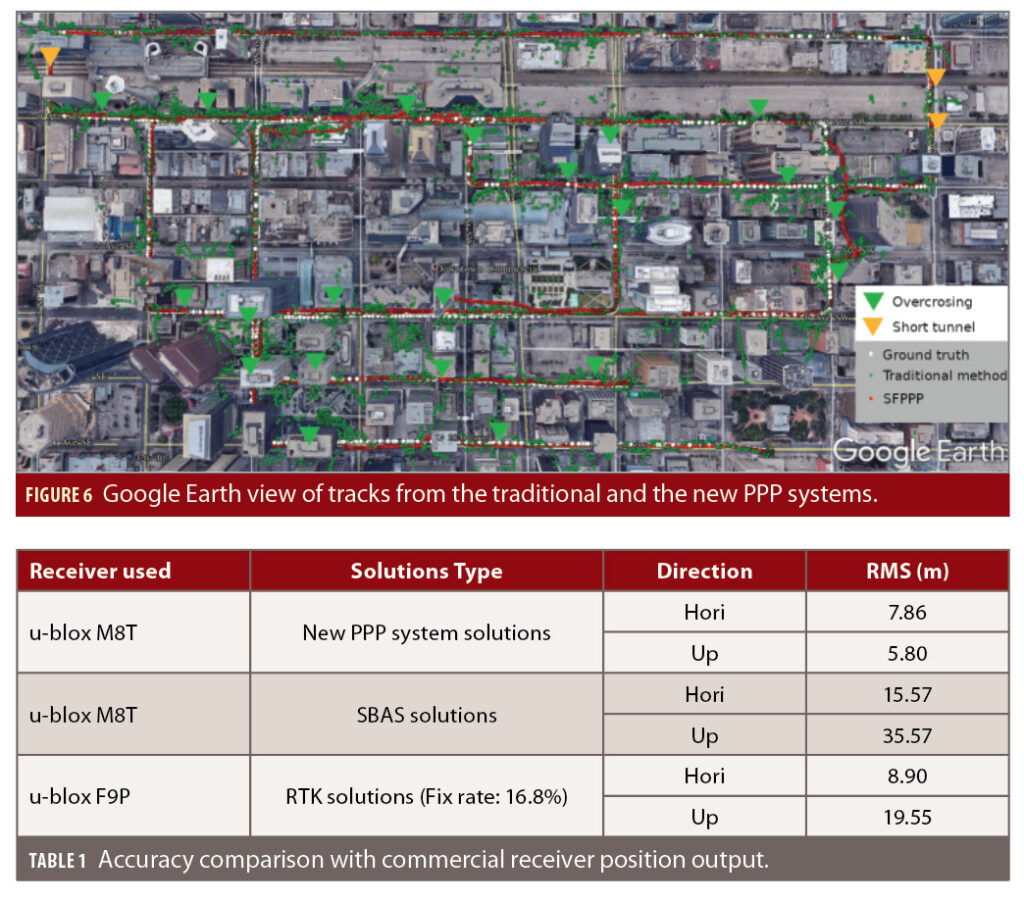
In addition to positioning errors and CDF plots, Figure 6 shows the position tracks of the position solutions from the traditional system and the new PPP system. Numerous large position errors are present for the traditional system especially in the cross-street direction, in a range up to hundred of meters in some places. As a comparison, the position track from the new PPP method stays close to the ground truth most times.
In addition to this internal assessment, the performance of the new PPP system is compared to the output from the commercial receivers. This provides an independent external assessment. As mentioned earlier, an additional receiver (a low-cost u-blox F9P dual-frequency multi-GNSS receiver) was used in the field tests in addition to the low-cost u-blox M8T single-frequency multi-GNSS receiver, connected to the same antenna through a GNSS signal splitter.
The in-receiver SBAS position output from the u-blox M8T and the in-receiver RTK position output from the F9P are compared to the position solutions from the new PPP system with the u-blox M8T. The results are given in Table 1. We can see that the availability of ambiguity-fixed RTK solutions from the receiver is low for the u-blox multi-frequency GNSS receiver (16.8%). The positioning accuracy improvement in the horizontal and up directions by the new PPP system using a single-frequency GNSS receiver (u-blox M8T) over the in-receiver position output is 49.5% and 83.7% for the u-blox M8T SBAS and 11.7% and 70.3% for u-blox F9P RTK.
Conclusions
A new PPP system with a low-cost single-frequency GNSS receiver can improve positioning accuracy in urban environments. With carrier phase as the principal observable, the system employes a novel weight scheme and a two-filters algorithm to improve GNSS positioning accuracy in urban environments. The positioning results from two land-vehicle kinematic tests demonstrate that the positioning accuracy could be improved by 83.6% and 93.1% in the horizontal and up direction compared to the traditional system. In comparison to independent real-time receiver output, the new PPP system solution outperforms the commercial receivers in test urban environments. The new weight scheme and the two-filters algorithm have the potential to improve multi-frequency PPP and RTK performance in urban environments. To further improve the robustness and accuracy of the developed system, an integration with a low-cost IMU should be investigated.
Authors
Zhitao Lyu s a Ph.D. student in the Department of Geomatics Engineering, University of Calgary, Canada. His research interest covers several fields including GNSS positioning in challenging environments and multi-sensor navigation algorithm development.
Yang Gao is a professor in the Department of Geomatics Engineering at the University of Calgary, . His research includes theoretical aspects and practical applications of satellite-based positioning and navigation systems. His current research focuses on high-precision GNSS positioning and multi-sensor integrated navigation systems.