A new method for multipath rejection employs a multicorrelator-based GNSS receiver with an extended Kalman Filter (EKF) as an iterative solver, replacing the conventional delay locked loop (DLL) code tracking. The technique significantly reduces the positioning error and has low complexity. It can therefore be implemented in a real-time processing environment.
GNSSs have a broad field of application, such as aeronautics or maritime navigation. Moreover, it can also be found in the civil sector. In these areas reliable and precise positioning is, under nominal conditions, already possible today. Such systems are very susceptible to multipath propagation, however, leading to performance degradation or even failure. This makes the use of GNSS receivers with safety critical applications such as autonomous cars or unmanned aerial vehicles a challenging task requiring additional solutions on the signal processing side. For this reason, many approaches to reduce the effect of multipath have been proposed.
Multipath denotes the coherent reception of reflected satellite signals. In this process, the line of sight (LoS) signal is superimposed by several delayed replicas of itself, which leads to a deformation of its cross-correlation function with the local signal replica of the receiver. The conventional DLL might provide biased results under such conditions. This in turn can cause positioning errors of multiple meters.
Currently, various approaches that can handle multipath environments range from detection to active mitigation systems. Signal-quality monitoring (SQM), for example through delta or ratio metrics, is commonly used to monitor satellites for any anomalies. However, the same metrics can also be applied to unveil the distorting effects of multipath environments. Once an affected satellite has been detected, it can be de-weighted in the PVT solution or excluded altogether.
To actually mitigate multipath signals several advanced code tracking loops have been proposed in the past. The most common ones depict the narrow correlator and the class of double-delta correlators (DDCs) with, e.g., the strobe correlator or the early-late slope (ELS) technique. These solutions are computationally inexpensive but tend to be in particular sensitive towards short-distance multipaths. On the positioning level a widespread approach is vector tracking. Here, all satellites are processed jointly so that individual multipath effects are suppressed. However, since the multipath is not actively removed, the position error increases with the number of affected satellites. Besides that, multipath rejection can also be incorporated to some extent in the physical structure of the receiver by using, e.g., choke ring antennas. This damps signals from low elevation angles and thus, reduces the effect of ground reflections.
Along with the pure mitigation approaches discussed above, there is also a group of techniques that aims to determine the parameters of the individual multipath components and suppress these additional signal paths accordingly. A commonly known method is the Multipath Estimating Delay Locked Loop (MEDLL). Here, the correlation function, sampled by a correlator bank, is matched with one generated from a multipath incorporating signal model. The multipath parameters are estimated using the maximum likelihood (ML) criterion. This allows to subtract the multipath components from the received signal. The remaining signal can then be tracked distortion-free with a conventional GNSS receiver. Alternative approaches exist using ML estimators, Bayesian solutions, or a combination of both.
Naturally, such solutions are much more computationally demanding than anything else mentioned before. This makes them challenging to implement in real-time systems. Besides that, there exist many techniques that make additionally use of antenna arrays. These are very effective and powerful solutions due to the enabled spatial signal processing. However, such arrays introduce higher cost for not only the antenna, but also the receiver hardware. Furthermore, in many applications the installation size is a crucial parameter, where large antennas would not fulfil the requirements.
Recently, a new iterative single antenna approach has been proposed by using an EKF. Here, the conventional DLL with early, prompt, and late is replaced with a correlator bank driven by the code delay estimate of the EKF. The underlying signal model of the EKF describes the radio propagation channel between a GNSS satellite and the user antenna with the help of a tap-delay line CIR model. The coefficients of the CIR model are the state parameters of the EKF which are needed to be estimated. This approach inherently allows for the consideration of multipath propagation effects and other signal distortions which can be modelled with respect to the propagation channel. Due to the low computational complexity of the EKF, it also depicts a promising solution for real-time implementations. The behavior has been demonstrated and evaluated with a few fundamental simulations. Further extensions and possible fields of application were shown in follow-up studies.
Here we pursue the EKF-based approach proposed, by showing that it suffers from ambiguities between delay estimate and CIR when applied to more realistic navigation scenarios. A solution to that is proposed by introducing an additional constraint. Moreover, the state and measurement model have been adjusted to comply with the requirement of non-complex delay estimates as well as allowing for acausal CIRs. The latter one is required to enable a correct channel estimation in case of imperfect delay estimates. The adjustments have been tested with simulations and actual measured data from a GNSS constellation simulator from GSS9000 series of Spirent.
Signal Model
The signal model in the following was originally proposed by R. A. Iltis and further investigated by A. Iliopoulos et al in 2017. A GNSS satellite emits periodically its pseudorandom noise (PRN) code sequence.
s¯ (t) ≡ s¯ (t − pTcode), ∀p ∈ Z,
where Tcode denotes the code period. For transmission it is modulated onto a carrier frequency and correspondingly down-converted on the receiver side. Due to the transmit and receiver filter a band-limited version of the ideal pulse sequence reaches the user, denoted as s(t) in the following. Furthermore, the radial distance between satellite and receiver causes the time dependant propagation delay τ (0)(t). In addition to that, channel characteristics, e.g., multipath propagation, as well as hardware imperfections lead to further signal distortions. These effects can be modelled by a filtering operation so that the baseband received signal is given by
where Tc is the chip duration of the individual chips in the PRN signal and η(t) is a zero mean complex white Gaussian noise with variance σ2. Due to the nature of PRN signals being almost uncorrelated for τ > Tc, the underlying improper integral has been approximated by limiting it to Tc. All remaining cross-correlation components are modelled with the noise term η(t).
Proposed Algorithm
The algorithm is a modified version of a solution proposed by Iliopoulos et al. First, the received signal is compressed to reduce computational load. A correlator bank has been used to project the measurement onto a smaller space and therewith, compress the data. For further computations, see the online version of this article.
An extension of the EKF formulation consists in the introduction of an additional constraint related to the position of the LoS signal associated channel tap in the CIR. Due to the interdependence of the channel coefficients h(l) and the code delay τ (0), there exists an ambiguity. A too small delay can be compensated by the LoS path being represented with a later tap in the CIR and vice versa. Therefore, we had to introduce a constraint holding the LoS path in place. This has been implemented through an additional constraining measurement.
Implementation Details
Precomputing Partial Derivatives. Several expressions can be precomputed in order to reduce computational load during runtime. One expression (shown online) is time-invariant and independent of the state vector. Hence, this part can be determined once in an initialization phase and remains constant throughout the entire tracking. In addition to that, the partial derivatives can be precomputed entirely.
PRN Filtering. As already mentioned in the signal model, the ideal PRN sequence s¯ (t) reaches the user with finite bandwidth due to receiver and satellite transmitter restrictions. Accordingly, the signal model considered that by using the band-limited version s(t). This signal is also required for the EKF measurement model. However, the exact filtering that s¯(t) experiences is usually not known. Therefore, s(t) is assumed to be simply a low-pass filtered version of s¯(t) with the cut-off frequency of either the satellite or the receiver, whichever has the smaller bandwidth. It turned out that this provides a good enough approximation.
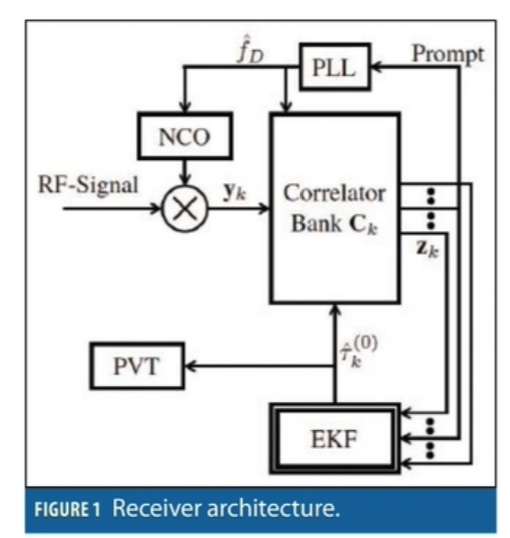
Receiver Structure. Figure 1 illustrates how the multipath detecting and mitigating algorithm can be integrated into a GNSS receiver. From the left side comes the radio frequency (RF) signal. It is first of all down-converted using a numerically-controlled oscillator (NCO) according to the current Doppler estimate fˆD provided by the phase locked loop (PLL). Therewith, one obtains the baseband signal yk which is directly fed into the correlator bank Ck.
All correlator outputs zk are processed by the EKF, whereas the PLL requires only the prompt correlator. In the EKF block the CIR and code delay estimation takes place. The latter one is used to drive the correlator bank so that it matches with the incoming signal yk. In addition to that, the delay estimate is required for the PVT solution.
Effect of Doppler. Until now it has been ignored that the Doppler shortens or stretches the received PRN signal. In fact, the local replicas in the correlator bank and the EKF measurement model would have to be constantly adapted accordingly. This would also entail that the partial derivatives in F update entirely every iteration leading to increased computational load. To avoid that, we made the following approximation. Our implementation relies exclusively on PRN replicas with zero Doppler used for the measurement model and the correlator bank. The latter is shifted according to current code delay estimate. When Doppler is present, the correlator bank is additionally shifted by half the Doppler introduced shortening or stretching. Therewith, one obtains a perfectly centred correlator bank.
The only approximation that has been made is that the local replicas are slightly longer or shorter than the actual received PRN signals leading to a negligible power loss due to the imperfect correlation and a minor mismatch between the measurement model and the received signals.
However, as the correlation is performed over only one code period Tcode, even the strongest possible Doppler introduced shortening or stretching lays in the region of 10−2Tc or less compared to the nominal period for GPS L1 C/A code. Thus, the approximation errors can be neglected for most applications.
Furthermore, the Doppler introduced shortening or stretching causes a carryover into the subsequent correlation. This is due to the circumstance, that the stacked received signal yk always holds the same amount of samples corresponding to the nominal code period Tcode. However, the actual code period deviates from that according to the current Doppler. To compensate for that, an additional correlator bank shifting is required. It is determined by the Doppler frequency and accumulates over time. This principle is also known from the conventional DLL implementation, where it is solved by relying on its own Doppler estimate. Since the EKF does not provide Doppler estimates, a carrier-aiding approach has been followed and fˆD from the PLL has been used.
Measurement Noise. To set up the EKF parameters correctly, one also requires the measurement noise variance σ2. One method to determine the parameter is as follows. Assuming non-normalized correlator outputs, one populates the correlator bank with truly random sequences that have the same amplitude as s(t). The variance of the obtained correlator outputs are then the diagonal elements of Rη,C. With that, σ2 can be determined accordingly.
Simulation
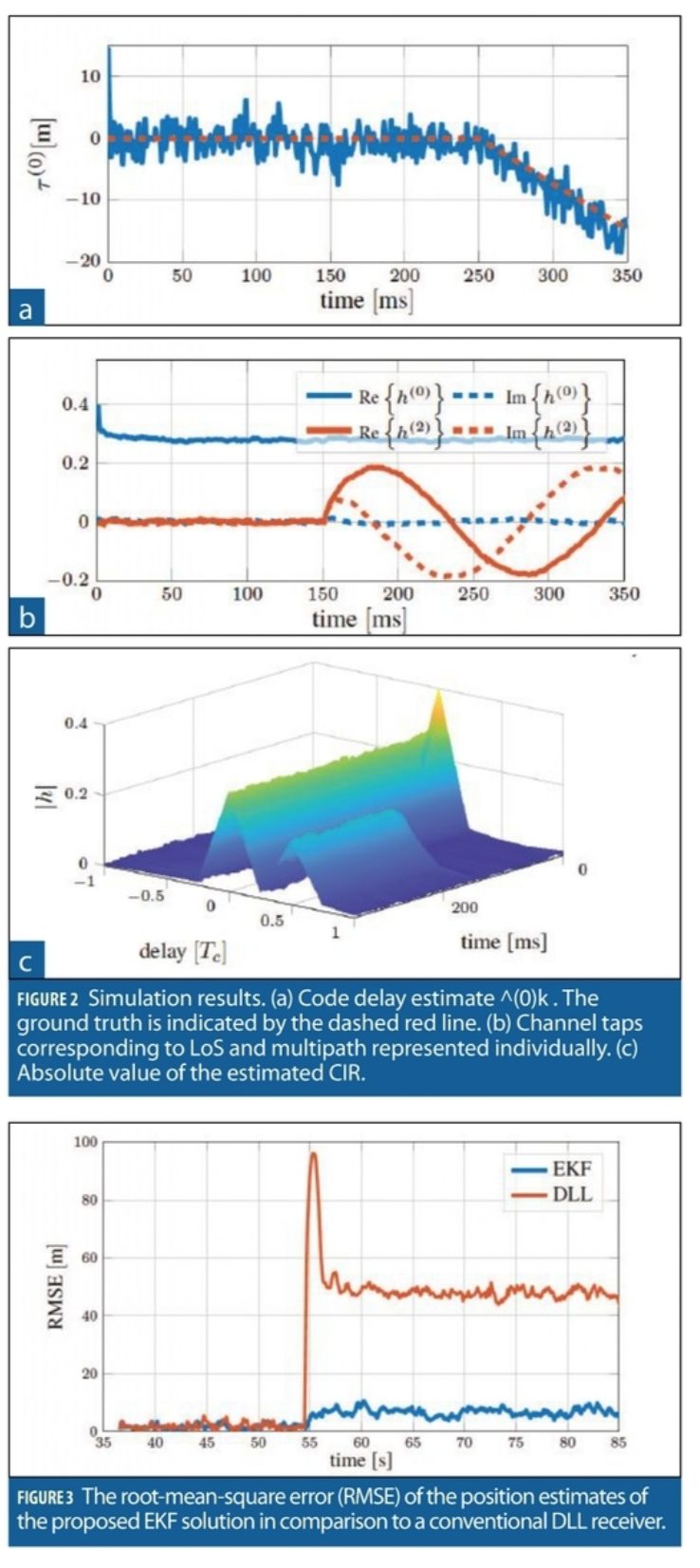
The following simulation has been performed to demonstrate the functionality of the algorithm. A scenario with a single GPS satellite received with 55 dB Hz Carrier-To-Noise-Ratio (C/N0) and zero Doppler at start using the L1 C/A code with Tcode = 1 ms has been investigated. After 150 ms a multipath appears with an additional path length and attenuation of 0.5Tc and 3 dB, respectively. The multipath has a code Doppler offset to the LoS of 5 Hz. Furthermore, the receiver uses a one-sided bandwidth of B = 4.092 MHz sampled at Nyquist frequency. Correspondingly, the local PRN replicas for the correlator bank and the measurement model are low-pass filtered according to B. The EKF uses a nine-tap CIR with a channel tap spacing of Th = Tc/4 leading to Nst = 19 states.
Figure 2a shows the obtained code delay estimate. One can see a short initialization phase where the initial code delay estimate converges towards the ground truth. At 150 ms the estimate shows its most dominant outlier. This is due to the activation of the multipath and the ensuing adaption of the EKF to the new conditions. The absolute value of the estimated CIR is in Figure 2c. The results meet expectations. Due to the imperfect initial LoS amplitude estimate the channel tap h(0) converges first of all towards its true value of around 0.28. Besides the LoS one can see the multipath appearing at 0.5Tc. Its amplitude is with approximately 0.19 meeting the expected 3 dB loss compared to the amplitude of the direct path.
Figure 2b represents the real and imaginary part of the estimated LoS and multipath channel tap l = 0 and l = 2, respectively. One can clearly see how the phase of the multipath signal rotates due to its frequency offset. It causes the constant interchanging of the real and imaginary part of h(2).
Hardware Demonstration
To demonstrate the capabilities of the proposed solution under realistic conditions, the algorithm has been tested with authentic GNSS signals. The signals have been generated on the L1 frequency band by the Spirent GNSS constellation simulator of the GSS9000 series and recorded as baseband signal samples with the help of the NI PXIe-5170 4-channel oscilloscope card.
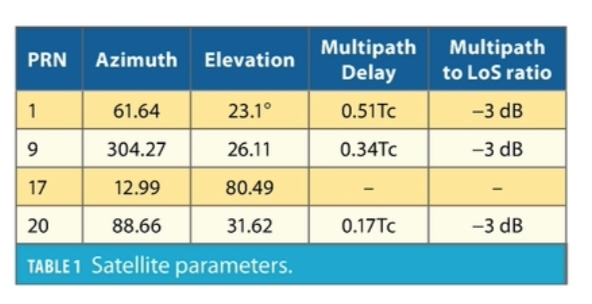
Here, a full medium Earth orbit (MEO) constellation with GPS satellites broadcasting the C/A code has been simulated. The receiver position is set statically to 48°N and 11°E with nine satellites in sight. Four satellites were used for the processing, where three out of the four selected ones are affected by multipath. See Table 1 for more details.All multipaths arise at the same time at around 55s.
The generated simulator signals were sampled at an IQ-rate of fs = 20 MHz with an RF front end that had a one-sided bandwidth of 6 MHz. The local PRN replicas for the EKF were low-pass filtered according to the latter. The remaining EKF parameters are given in the online version of this article.
Tracking Results
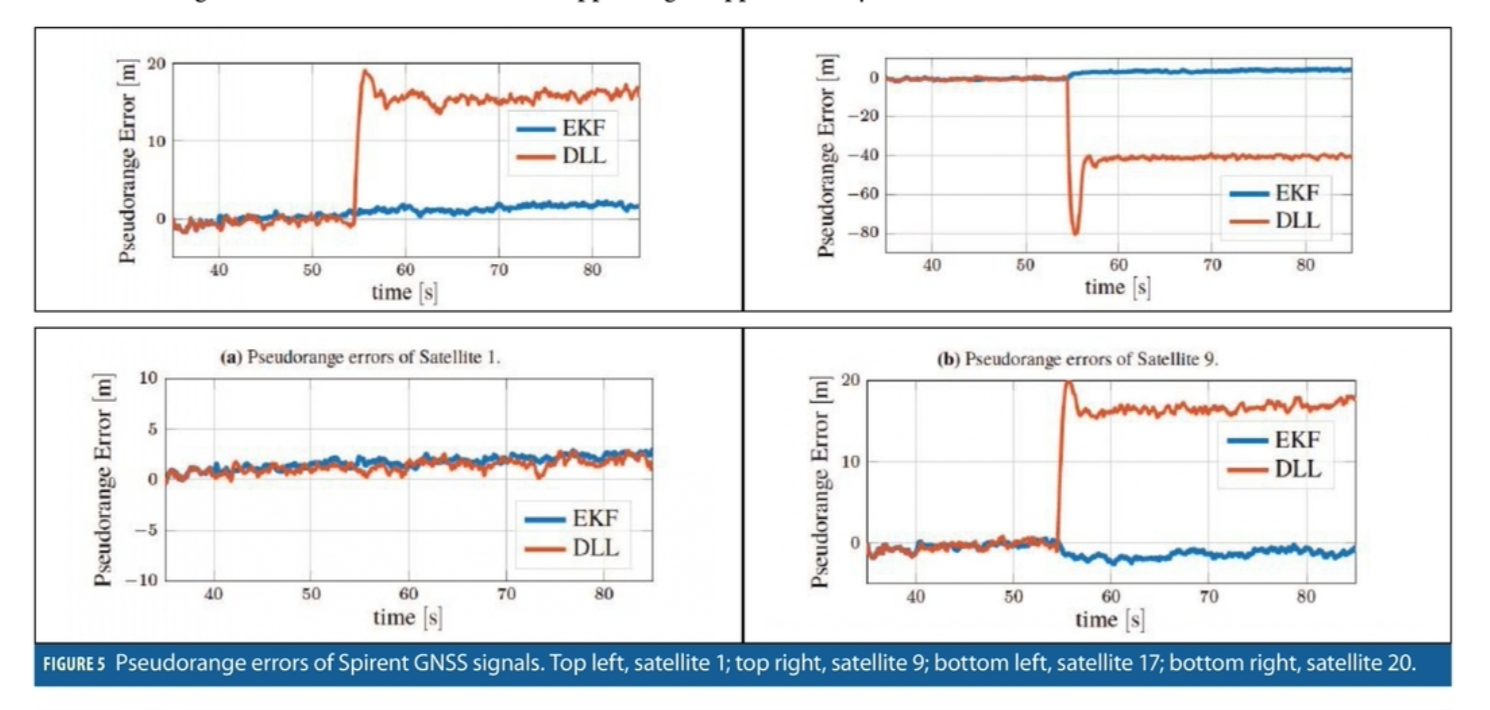
The estimated CIRs are given in Figure 4. The LoS paths are all well locked at 0Tc, thus, the introduced constraint in the measurement model of the EKF seems to work as expected. Furthermore, for the three interfered satellites the additional signal components are appearing at approximately 55s. The multipath delays correspond to the values given in Table 1. When the multipath has a delay which is not directly covered by a channel tap, the neighboring coefficients are weighted correspondingly, as one can see in 4b and 4d.
The resulting pseudorange errors before the PVT solution are given in Figure 5. In all graphs the first seconds have been cut of as the EKF has been enabled only after 40 s. For the satellites 1, 9, and 20 one can clearly see how in the DLL case the error jumps at 55 s due to the enabled multipaths. On the other hand, the EKF can maintain mostly its track. Merely for satellites 9 and 20 an additional error of around 2 m has been obtained. Figure 3 compares the position RMSE of the conventional receiver with the one achieved by the proposed EKF solution. Due to the severe multipath environment the DLL is heavily distorted after 55 s leading to errors of up to 50 m in its steady state. In contrast, the EKF manages to achieve errors on average as low as 6.7 m with multipaths. During the multipath free part in the beginning of the scenario, both solutions perform comparable. Note, since the time to first fix (TTFF) took 36.6 s seconds in this example, no position estimates were available before that.
Conclusion
This article studied the case of GNSS in multipath environments and proposed a multipath estimating and mitigation algorithm. It consists of an EKF replacing the conventional DLL.
The proposed EKF aims at delivering code delay estimates which are more robust against disturbing multipath phenomenon than in case of using a DLL as its measurement model incorporates the radio propagation channel. Thus, besides a reliable code tracking, one also obtains an estimate of the CIR.
Simulations as well as hardware implementations demonstrated the functionality of the algorithm. The code tracking was barely affected from multipath and the estimated CIR represented well the propagation channel. This led to significant pseudorange and PVT error reduction, even under severe multipath conditions.
In a future work one should investigate the possibility to add Doppler estimation to the EKF to not rely on carrier-aiding.
Acknowledgment
This article is drawn from a paper presented at the Institute of Navigation International Technical Meeting, January 2021.
Authors
Christian Siebert works in the Institute of Communications and Navigation of the German Aerospace Center (DLR) in Oberpfaffenhofen and is a Ph.D. candidate at Rheinisch-Westfälische Technische Hochschule (RWTH) Aachen University. His research interests include multipath detection and mitigation.
Andriy Konovaltsev is a research assistant in the Institute of Communications and Navigation of DLR. His main research interest is in application of antenna array signal processing for improving performance of satellite navigation systems in challenging signal environments.
Michael Meurer is the director of the Department of Navigation of DLR and a professor of electrical engineering and director of the Chair of Navigation at RWTH Aachen University. His current research interests include GNSS signals, GNSS receivers, and navigation for safety-critical applications.






