Multipath is a major phenomenon that degrades the integrity of GNSS-based navigation services. Under multipath, a receiver Delay-Lock Loop (DLL) does not correctly estimate the actual peak of the correlation curve, resulting in ranging errors. To overcome this effect, mitigation techniques have been developed, a detailed discussion of which
is found in Bhuiyan and Lohan (Additional Resources). As a general observation, some of these mitigating techniques attempt to minimize the effect by modifying the receiver hardware or tracking structure and others try to jointly estimate the multipath parameters. Among these well-investigated mitigation techniques, the selection of least distorted measurements is receiving attention in the context of GNSS multi-constellations in which case the number of available signals is large enough to de-weight or exclude faulty ones without significant degradation in solution geometry. In this context, SQM techniques have been developed to detect multipath distortions by incorporating monitoring correlators at the tracking level. The general approach is based on the linear or nonlinear combination of different early-late monitoring correlators to define symmetric and asymmetric test statistics and detect multipath distortions in the tracking correlation peaks. The correlator output samples are evaluated and integrity warning is set when the SQM metrics deviate from nominal values.
While different SQM metrics have been defined and extensively applied for GNSS multipath detection, little investigation has been conducted to provide insight on how theoretically sensitive and effective these metrics are under different scenarios. It has been shown that multipath affects SQM statistics (e.g., mean and variance) by distorting the correlation peak, but there is no analytical discussion about how sensitive such an approach is for detection. Some works show that SQM-based monitoring techniques can be used for multipath reduction by excluding or de-weighting affected measurements, but their effectiveness is an issue requiring more investigations under different tracking and signaling strategies.
This article evaluates the performance of SQM techniques under a broad range of multipath scenarios. In the sequel, after modelling the received GNSS signals in the tracking output, monitoring correlators are defined based on their relative code delays from the reference tracking correlators. A Double-Delta SQM metric is defined as a basic test statistic to detect distortions. SQM metric variation profiles are then proposed as a function of multipath relative delay and power. It is shown that such profiles, along with conventional multipath error envelopes, provide an appropriate framework to jointly analyze the sensitivity and effectiveness of the SQM approach under different multipath scenarios. SQM variation profiles are extracted and discussed for the Binary Phaseshift Keying (BPSK(1)) and Binary Offset Carrier (BOC(1,1)) signaling schemes. Two different tracking discriminators, namely Narrow Correlator (NC) (See Van Dierendonck et alia, Additional Resources) and High Resolution Correlator (HRC) (McGraw and Braasch, Additional Resources), are considered. These tracking strategies are commonly used in many receivers to mitigate multipath. Field data analysis is carried out to validate the analytical discussion and examine SQM detection performance under real static and kinematic multipath scenarios.

Signal Model
The received Intermediate Frequency (IF) signal is modeled as a combination of digitized signals corresponding to different Pseudorandom Noise numbers (PRNs) as described by Misra and Enge (Additional Resources)
Equation (1) (see inset photo, above right, for all equations)
where I is the PRN index, L is the number of satellites, CI is the power of the received signal from the Ith satellite, bI is the binary navigation data and cI is the spreading code used to modulate the navigation data; τI, fd,I and ϕI are code delay, Doppler frequency and carrier phase introduced by the communication channel; fIF is the IF and fs = 1/Ts is sampling frequency. ηfe (nTs) is front end complex zero mean Gaussian noise.
For each PRN, a reference tracking correlator multiplies the received signal by a corresponding replica and the samples are integrated over a coherent integration time period. The output of the Ith channel at time kNsTs (kth coherent integration epoch) is given by
Equation (2)
where Ns is the number of samples in the coherent integration period. Using a sum of geometric series, Equation (2) becomes
Equation (3)
where the effect of bit transition is neglected due to an assumed bit synchronization process; the index I is omitted for simplicity. Δτ0 = τ − ̂τ, Δf = fd − f̂0 and Δφ0 = φ − ̂φ are code, frequency and phase offsets between the received and the replica signal generated by the reference tracking correlator. NTs is the coherent integration time, also noted by TI • η consists of inphase and quadrature-phase Gaussian noise and Rτ(Δτ0) is the correlation function which is related to the choice of the GNSS signaling scheme. When the received signal is stabilized in PLL mode, it is assumed that there are no tracking code and phase offsets and thus the in-phase output of the ith early or late correlator is defined in the code-delay domain as
Equation (4)
where Tc is the chip duration and uiTc denotes the spacing of the ith early (for ui < 0) or late (for ui > 0) correlator from the reference prompt correlator. ηIui is the corresponding in-phase noise described above. Since the tracking loops are locked and the received signal is tracked in PLL mode, the in-phase component is considered. If the receiver operates in a non-coherent mode, both in-phase and quadrature-phase components should be taken into account.
SQM Metric Definition
SQM metrics are defined based on the linear or non-linear combination of tracking and monitoring correlators. The tracking correlators are used to track the signal and the monitoring correlators are used for quality monitoring. The conventional Double-Delta SQM metric (also known as Delta test) is considered as it is commonly used as a basic SQM metric in detecting GNSS distortions. The Double-Delta SQM metric is defined here based on the difference between two pairs of tracking and monitoring early-late correlators normalized by the prompt correlator
Equation (5)
where the tracking and monitoring early-late correlator spacings are chosen as 0.2 and 1 chips. I0 is the in-phase output of the prompt correlator. At each synchronized correlation epoch, the constituent components of the defined SQM metric have the same binary data with either a positive or negative sign (i.e., +1 or -1) in the corresponding numerator and denominator. Therefore, the navigation data has no effect on the SQM metric outputs. Under nominal conditions, in low multipath open sky environments and the absence of other GNSS signal degradation errors, the output of the SQM metric is a random process whose statistical properties are determined based on the location of the constituent correlators and receiver noise. The methodology of the SQM statistical analysis can be found in Pirsiavash et alia in Additional Resources, where numerical results have been presented for the mean and variance of the defined SQM metric.
Performance Analysis and SQM Variation Profiles
Performance evaluation is conducted by extracting SQM variation profiles and comparing them with the conventional multipath ranging error envelopes. As mentioned before, the analytical discussion of performance includes NC and HRC discriminators whose DLL discriminators are defined as
DNC = (I-dtrk I2−I+dtrk I2) (6)
DHRC = (I-dtrk I2−I+dtrk I2)−0.5(I-dtrk−I+dtrk) (7)
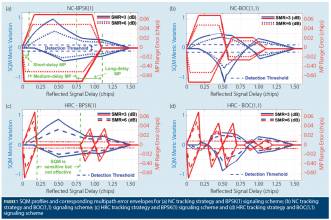
where a coherent tracking procedure is assumed and thus the in-phase tracking outputs are used. dtrk is set to 0.2 chips to build up the tracking discriminator functions and extract the corresponding tracking range error envelopes. These envelopes are shown in Figure 1 (right-hand vertical axis in red) for 3 and 6 dB Signal-to-Multipath Ratio (SMR) values and BPSK(1) and BOC(1,1) signaling schemes. To extract these envelopes, a single reflection is considered and the relative delay of the reflected signal with respect to Line-Of-Sight (LOS) signal is swept through a range of values to assess DLL code misalignment and resulting tracking range errors for in-phase and out-of-phase multipath components. Figure 1a also determines the approximate range of short, medium and long delay multipath considered here for 1 megahertz chipping rate. Reflected signal delays less than 0.1 chips (about 30 meters for the GPS L1 C/A case) are considered as short-delay multipath; a range of 0.1 to 0.75 chips is considered for medium-delay multipath and long-delay multipath covers reflected signal delays longer than 0.75 chips.
Figure 1 shows that for short-delay multipath the error envelopes are almost the same for all tracking strategies and signaling schemes. For path delays longer than approximately 0.5 chips, when NC is used as the tracking strategy, the corresponding tracking range error for the BOC(1,1) modulation is less than (about one third of) that of the BPSK(1) signal. This is because of the difference in the shape of the correlation functions for BPSK(1) and BOC(1,1) signaling schemes. For the HRC technique, the maximum tracking range error is the same for both signals under the effect of short-delay multipath. While the BPSK(1) ranging error is reduced to zero under medium-delay multipath, the tracking range error of the BOC(1,1) is significantly lower than that of the BPSK(1) signal for a long-delay multipath scenario.
To extract the SQM variation profiles shown in Figure 1 (left-hand vertical axis in blue), a similar methodology was used. A single reflection is considered and then the relative delay of the reflected signal is swept through a range of values to evaluate SQM metric outputs for in-phase and out-of-phase multipath components. It is observed that the SQM variation envelopes take their maximum absolute values around 0.5 chips where the late monitoring correlator is overlapped by the peak of the reflected correlation curve. When the multipath correlation curve passes the late monitoring correlator, the SQM variation envelopes decrease until the multipath correlation curve no longer overlaps with tracking and monitoring correlators for multipath signal delays greater than 1.5 chips. For the BOC(1,1) signaling scheme, due to the different shape of the BOC(1,1) correlation function, the reduction in variation envelopes shows a different behavior between 0.5 and 1 chips. In all cases, a lower SMR and consequently higher level of multipath relative power result in higher SQM variations as expected. For a Carrier-to-Noise-density ratio (C/N0) value of 45 dB-Hz (decibel-hertz), detection thresholds have been set to three times the corresponding nominal Standard Deviation (SD) to satisfy a false alarm probability of 0.0027.
The SQM profiles are now being used to evaluate the theoretical sensitivity and effectiveness of the SQM metric in multipath detection. SQM “sensitivity” and “effectiveness” are first defined as the critical keywords for the subsequent discussion.
SQM Sensitivity and Effectiveness for Multipath Detection
The sensitivity of the SQM approach is based on the magnitude of the variation profiles. If the SQM outputs exceed a given threshold, the effect of multipath is detected and the SQM method is considered sensitive. Otherwise, the multipath effect is not detectable and the SQM metric is therefore not sensitive.
Effectiveness is based on the multipath error magnitude. An approach is considered effective when the threshold excess of the SQM outputs coincides with a significant range error on the corresponding measurements. Effectiveness is important since ideally SQM based measurement weighting should be based on it and not on sensitivity.
Based on the aforementioned definitions and considering the SQM profiles shown in Figure 1, the following conclusions can be made regarding the sensitivity and effectiveness of the SQM metric under different multipath scenarios.
- For short-delay multipath, the effectiveness of the SQM metric is almost the same for all tracking strategies and signaling schemes. For this range of multipath delays, the SQM detection outputs can be effective when the range error envelopes take non-zero values. However, due to the low overall sensitivity of the SQM metric for the short-range multipath delays, it is possible that the resulting SQM values do not exceed the detection thresholds and thus multipath remains undetected. As illustrated in Figure 1, multipath with relative delays less than 10 meters is not detectable for either NC and HRC discriminators for the given signal parameters and receiver settings.
- For medium and long-delay multipath, when the NC discriminator and BPSK(1) modulation are used, metric deviations from nominal values (sensitivity) coincide with nonzero tracking range error envelopes. This means that the SQM detection results can be exploited effectively to reduce the imposed multipath error by de-weighting (or excluding) distorted measurements (effectiveness).
- When the NC discriminator is used, effectiveness under BOC(1,1) signaling is less than that for BPSK(1) for path delays longer than 0.5 chips. In this area, the overall ranging error is about one third of that of the BPSK(1) signal. In this scenario, according to the SQM profiles, the sensitivity of the metric is also lower due to the different shapes of the correlation function.
- In the case of medium-delay multipath, HRC discriminator and BPSK(1) signaling schemes, the SQM metric will not be effective since the ranging error is negligible. In this scenario, relying on SQM detection results to de-weight or exclude detected measurements may even impose position errors due to geometry degradation. For BOC(1,1), the SQM can be effective for some intervals of medium-delay multipath when tracking range error envelopes take non-zero values.
- For long-delay multipath, when HRC discriminator is used, a lower SQM performance is observed for the BOC(1,1) signaling scheme where the sensitivity of the SQM metric is less and the multipath performance of the BOC(1,1) is significantly better than that of the BPSK(1) modulation.
- In all cases, lower SMR and consequently higher levels of multipath relative power result in higher sensitivity as expected. For a given SMR value, a higher C/N₀ increases sensitivity by reducing the nominal standard deviation of the metric and thus lowering the resulting detection threshold.
The SQM variation envelopes show the maximum level of SQM sensitivity under specific multipath delay and power. In practice, due to satellite motion and other effects, there are always phase variations between LOS and multipath signals causing SQM outputs to fluctuate between in-phase and outof- phase envelopes. This will drop the practical sensitivity of the SQM metric for multipath detection. The same argument applies to multipath range error envelopes and consequently SQM effectiveness.
Field Data Analysis
To validate the sensitivity of the SQM approach in real environments, field tests were conducted for static and kinematic multipath scenarios. These tests were carefully designed and considered to provide controlled conditions corresponding to the above analysis.
Static test scenario
GPS L1 C/A data was collected using a static antenna surrounded by buildings with smooth surfaces acting as short-range reflectors as shown in Figure 2. IF samples were collected using a front-end receiver with a 10 megahertz sampling frequency. The IF data was then analyzed with a software receiver to extract SQM outputs for different PRNs. A narrow correlator discriminator with 0.2 chips early-late spacing was implemented. Monitoring correlators were placed 1 chip apart and the coherent integration time was 20 milliseconds.
Figure 3 shows Code-Minus-Carrier phase (CMC) and C/N0 measurements for selected PRNs. C/N0 values are computed using the Narrowband-Wideband Power Ratio (NWPR) method (See Parkinson and Spilker, Additional Resources). CMC measurements are extracted to characterize code multipath errors (See Braasch, Additional Resources) where carrier phase measurements are subtracted from the corresponding pseudorange measurements. In addition to code and carrier noise and multipath errors, the subsequent outcome includes carrier phase ambiguities and twice the ionospheric errors (due to ionospheric code delay and phase advance). The effects of ambiguity and ionosphere are approximated and removed through polynomial curve fitting. Neglecting residual effects of carrier phase noise and multipath errors, the resulting values are a valid measure of code multipath and noise. PRN 23 can be considered to be in a multipath-free measurement while PRN 22 is heavily affected as shown by corresponding CMC values.
Figure 4 shows monitoring results for the Double-Delta SQM metric calibrated and normalized using its nominal SD. In this normalization, the C/N0 values are smoothed by a moving average with length of 60 seconds. Detection thresholds are fixed to ±3 for the normalized metric. The M of N detection strategy is used by taking windows of N samples and comparing them to the predefined threshold. If M or more samples exceed the threshold, then the detection output will be 1 and otherwise 0. This procedure is repeated for each step of the sliding search window. With this detection strategy, the overall probability of false alarm in N trials is given by Kaplan and Hegarty (see Additional Resources)
Equation (8)
Pfa is the false alarm probability in each trial equals to 0.27% under the assumption of normal distribution for the SQM metric and ±3SD as the detection threshold. Figure 4 shows monitoring results for PRN 23 and 22 when N = 500 (samples or 10 seconds) and M = 12, 15 and 20 are chosen to satisfy the overall probability of false alarm around and 2 °— 10-8, 1.6 °— 10-11 and 1.8 °— 10-14, respectively. As shown in Figure 4a, the output of the designed detection algorithm for PRN 23 is zero for almost all epochs identifying this PRN as clean. In the case of PRN 22 (shown in Figure 4b), while medium effect of multipath (according to its CMC measurements) remains almost undetected, code measurements with errors above 5 meters are clearly detected.
Kinematic test scenario
Figure 5 shows the data collection environment and setup for kinematic data set 1. The GPS L1 data was collected with an antenna mounted on a cart moving at a velocity of 0.5 m/s through a suburban area. The data was down-converted and sampled with a 20 megahertz sampling frequency. The GPS signals were then acquired and tracked in the software receiver (with the same settings mentioned before) to monitor the signal quality as well as SQM metric outputs.
Figure 6 and Figure 7 show PRN7 monitoring results. According to CMC measurements, multipath during the data collection is generally low and errors do not exceed 5 meters except for some epochs between 20 seconds and 60 seconds. The corresponding SQM results were then extracted for each 20 milliseconds of the coherent integration time. The metric was calibrated and normalized using its nominal standard deviation. In this normalization, the C/N0 values were smoothed using a moving average window. Compared to the static scenario, the length of the smoothing window was reduced to 4 seconds due to the dynamic characteristic of the data and consequently faster multipath variations as a function of time. The detection thresholds were fixed to ±3 times the normalized SD. The length of the sliding search window (N) was 2 seconds and M = 5, 6 and 7 were chosen to detect multipath with overall false alarm probabilities 8.7 × 10-6, 3.7 × 10-7, 1.3 × 10-8, respectively. The sensitivity of the SQM metric is limited to epochs whose multipath error is in the order of 5 meters or more. For M ≥ 9, The SQM detection output is zero for all epochs and multipath errors remain undetected.
A second kinematic data set was collected in the urban canyon shown in Figure 8a. The building on the right has smooth surfaces considered as strong reflective sources. The GPS L1 data was collected with the same setup but mounted on a vehicle driving at a velocity of 1 m/s in the west direction through the canyon.
Figure 9 and Figure 10 show the PRN 21 monitoring results during the different segments of the trajectory. Similar results were observed for other PRNs. The data collection was started in a fairly open sky environment whose first 5 seconds is shown in the figures. The vehicle then passed through the canyon for 100 seconds and ended in a fairly open sky environment (the last 35 seconds). Corresponding multipath was observed in the CMC measurements shown in Figure 9 where segments with relatively strong multipath are marked in red while medium and low multipath segments are marked in yellow and green.
Figure 10 shows the SQM and detection results for PRN 21 with the same settings as mentioned previously. This time M = 7, 9 and 11 were chosen over a 2 second sliding search window (N). With this assumption, the overall false alarm probabilities are approximated by 1.3 × 10-8, 1.2 × 10-11, 1 × 10-14, respectively. In Figure 10, the detection output for the regions with low multipath (green region shown in Figure 9) is zero, indicating clean range measurements for PRN 21. It is also shown that the medium effect of multipath (multipath is below 3 meters according to CMC measurements) is buried under the SQM metric noise and remains almost undetected. However, for those epochs strongly affected by multipath (when multipath error is in the order of 5 meters or more), the SQM metric is mostly sensitive and the metric outputs show multipath occurrence.
Summary and Conclusions
We analyzed the performance of SQM approach for multipath detection. The Double-Delta SQM metric was investigated by incorporating tracking and monitoring correlators under different tracking and signaling schemes. Different scenarios and comprehensive analyses were provided. The results extracted for 1 megahertz chipping rate show that although SQM is sensitive to medium and long-delay multipath, its effectiveness differs based on the selection of tracking strategy and signaling scheme. Therefore, for a given scenario, its effective utilization requires the joint analysis of both sensitivity and effectiveness as proposed here. Under short-delay multipath scenarios (especially for multipath delays below 10 meters), the range measurements multipath effect remains mostly undetected for a realistic range of multipath power values. In all cases, a lower SMR results in higher SQM sensitivity and effectiveness, as expected. For a specific level of SMR, higher C/N0 increases SQM sensitivity by reducing the nominal variance of the SQM metric and thus lowering the corresponding detection threshold. The analysis of actual measurements in static and kinematic multipath scenarios validates the analytical discussion where the SQM metric is mostly sensitive to multipath errors larger than 5 meters for given receiver settings and monitoring parameters.
Additional Resources
[1] Bhuiyan, M. Z. H. and E. S. Lohan (2012) “Multipath Mitigation Techniques for Satellite-Based Positioning Applications,” Global Navigation Satellite Systems: Signal, Theory and Applications, Jin, S., Ed.; InTech: Rijeka, Croatia, 2012; pp. 405–426.
[2] Braasch, M.S. (1995) “Isolation of GPS Multipath and Receiver Tracking Errors,” Journal of Institute of Navigation, vol. 41, no. 4, pp. 415–434.
[3] Kaplan, E.D. and C.J. Hegarty (2006) Understanding GPS Principles and Applications, 2nd Ed., Artch House, Norwood, MA, ISBN 1-58053-894-0.
[4] McGraw, G. A. and M. S. Braasch, M. S. (1999), “GNSS multipath mitigation using Gated and High Resolution Correlator concepts,” In Proceedings of the National Technical Meeting of the Satellite Division of the Institute of Navigation, San Diego, CA, January 25-27, pp. 333–342.
[5] Misra, P. and P. Enge (2006) Global Positioning System: Signals, Measurements and Performance, 2nd ed.; Ganga-Jamuna Press: Lincoln, MA.
[6] Parkinson, B.W. and J. J. Spilker (1996) Global Positioning System: Theory and Applications, American Institute of Aeronautics and Astronautics Inc., Washington, DC, vol. 2.
[7] Pirsiavash, A., A. Broumandan and G. Lachapelle (2017) “Characterization of Signal Quality Monitoring Techniques for Multipath Detection in GNSS Applications,” Sensors, vol. 17, no. 7, 1579.
[8] Van Dierendonck, A. J., P. C. Fenton and T. Ford (1992) “Theory and performance of narrow correlator spacing in a GPS receiver,” Journal of The Institute of Navigation, vol. 39, no. 3, pp. 265-283.