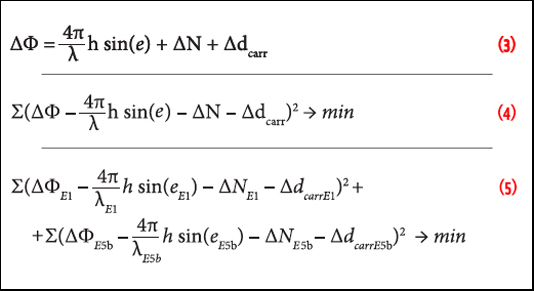Galileo satellites 5 and 6 (E18, E14) were declared unusable in February 2021 after reports indicating repeatable daily problems with RTK. This article explores the possible impact of deviant elliptical orbits on the performance of RTK and finds that there is no reason to expect any anomalies caused by high orbit eccentricity per se. Thus there is no reason to declare the satellites unhealthy.
The saga of Galileo satellites 5 and 6 (E18, E14) will be remembered in the history of satellite navigation as a dramatic story of successful recovery from what seemed to be a failed mission. Erroneously launched in 2014 into highly elliptical orbits, quite far from their originally planned destinations, the two satellites were moved to acceptable moderately elliptical (eccentricity 0.162) orbits, where their non-standard orbit parameters would fit the navigation message and could be used in a regular way.
After a few years of steadfast effort by ESA and related organizations, health flags on both satellites were finally cleared on Nov 30, 2020. Thus, two more usable satellites were added to the Galileo constellation. The commissioning of E14 and E18 satellites into service went uneventful; the vast majority of receivers survived the switch.
However, repeatable daily problems with RTK, a precise phasedifferential positioning technology, were reported for some receivers. Upon investigating these reports, on Feb 16, 2021, GSA decided to change the status of the two elliptical satellites back to unhealthy. It was deemed unfair that some commercial users should have their RTK solutions degraded, while others would benefit. This decision stripped Galileo users of two apparently usable satellites, thus weakening the Galileo constellation which is still incomplete.
In our opinion this step was taken a bit too rashly. Stricto sensu, no GNSS system provides guarantees for RTK. In fact, RTK is simply out of scope of the Galileo ICD as well as of the ICDs of other major GNSS systems. At the same time RTK, being the most precise GNSS-based positioning technology, is universally used in both commercial and scientific applications. This fateful GSA’s decision of Feb 16, 2021 was probably the first one in GNSS history when the constellation was changed following isolated complaints from RTK user community even though RTK does not stand in the list of Galileo services and is not officially monitored by the ground control segment.
RTK, by its nature, is a ‘trick’, which allows user receivers to cancel out most GNSS errors but has an inherently limited range of applicability. Main keys to the performance of RTK are in the hands of service providers and designers of user algorithms which, in their complexity, go far beyond original ICDs. It is well known that the performance of RTK is primarily an issue of rover-base compatibility and algorithmic robustness, depending only in part or indirectly upon the factors defining performance of GNSS systems as it is defined in their ICDs.
We summarize our experience with E14 and E18 satellites, with particular attention to the impact on RTK performance, which, to our knowledge, did not receive yet sufficient attention in literature. Although quite a few research papers were published reporting on the positioning performance with the use of elliptical Galileo satellites—mostly with positive conclusions—no inquiry into the functioning of differential positioning algorithms running in receivers tracking E14 or E18 signals has hitherto been made.
The status of discussion still allows for a suspicion that even in a good generic receiver some regular malfunctioning of the RTK navigation solution would be possible due to inherent anomalies of elliptical orbits.
We believe that this is not the case. We argue that with a correct implementation of RTK algorithms, following Galileo ICD and GNSS theory, the deviant elliptical orbits are computed with the same precision as normal orbits except for a limited degradation of accuracy provoked by occasionally high age of ephemeris. Such occurrences can be reported by Galileo itself in terms of SISA index (I/NAV word 3, F/NAV page 1) without the need to exclude two perfectly functioning satellites from the constellation.

Challenges of Eccentric Orbits and Uplink Outages
One very real nonconformity of elliptical satellites to the Galileo ICD is the absence of almanacs; high eccentricity does not fit the range of permitted values of almanac’s orbit parameters. But almanacs, in the traditional GNSS paradigm, are only meant to aid with the acquisition of signals. Once a satellite is tracked, almanacs are no longer needed. Ephemerides can be used to compute position as well as satellite’s elevation and azimuth, the two important parameters which have multiple uses in receivers: to predict visibility, calculate troposphere delays, refine error models etc. In fact, most today’s GNSS receivers include dedicated hardware acquisition modules, which perform so-called ‘wide search’ and do not depend upon availability of almanacs.
Another increasingly popular alternative to almanac-based initialization is a quick delivery of latest ephemerides via general communication networks (Assisted GNSS). Of course, receivers of a more traditional design which use stored almanacs for signal acquisition, will have problems acquiring signals of E14 or E18 satellites. But, once their signals are acquired in one way or another, the calculation of position will not suffer from their deviant orbit parameters. Let us go into some further detail to support this statement.
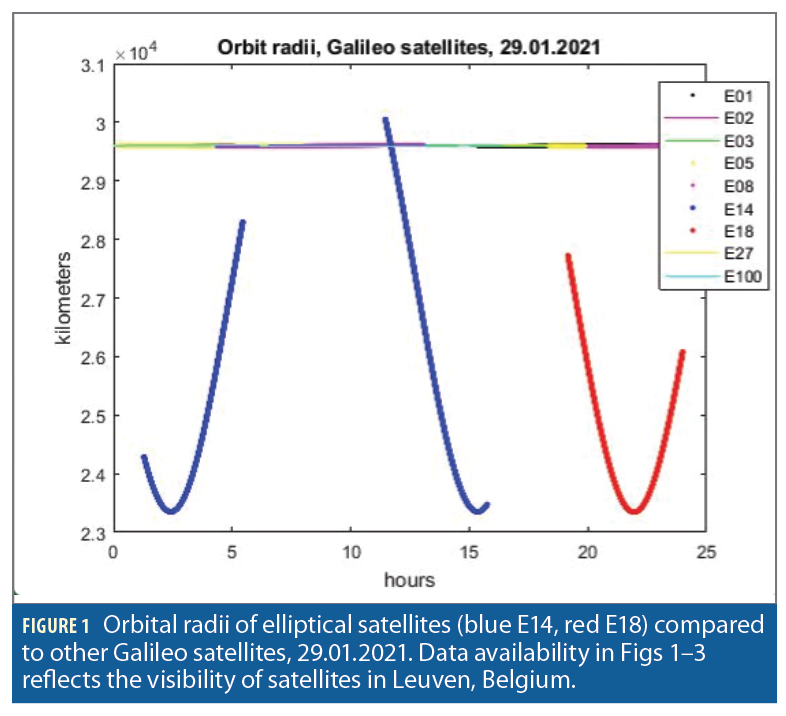
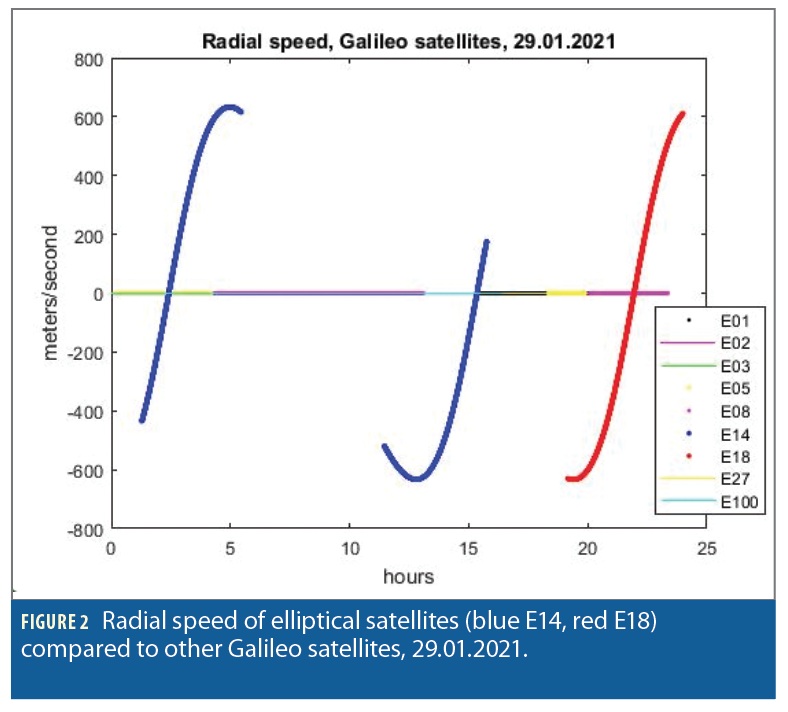
The main peculiarity of eccentric orbits is in large variations of their orbit radii (Figure 1). Satellite’s radial speed is, accordingly, quite high (Figure 2). The relativity correction, being proportional to the radial speed, is also much higher than with normal satellites (Figure 3). But although these and some other orbit-related parameters have values out of a nominal range, these parameters can still be computed with an acceptable level of precision comparable to that of normal satellites. The formulas of Galileo ICD which are used to calculate satellite positions as a function of GNSS time are geometrically precise and cause no extra errors within their intervals of applicability.
The problem is rather that with elliptical satellites, due to higher variability of their orbit radii, the actual limit of applicability is about 2-2.5 hours. In reality, the age of ephemeris sometimes gets as high as 3 hours, the official maximal allowable age of ephemeris being 4 hours. Based on the data presented in “Signal in space error and ephemeris validity time evaluation of Milena and Doresa Galileo satellites,” by Robustelli, U., Benassai, G. Pugliano, G., in Sensors, 19(8), 1786 (2019), a few days were identified where the radial orbit errors of E14 and E18 satellites reached values about 10m with ephemeris age of 2.5–3 hours, whereas predicted orbits of other satellites remained bound within expected limits of 1–2m. In what follows we show that similar periods still occur on a regular basis.
Of course, the age of ephemeris reaches such high values quite rarely. Most of the time it stays on the level of 20-30 min. Periods of high ephemeris age occur due to the deficit of available antennas and transmitters used to upload Galileo ephemeris data to satellites. The number of those ‘dishes’ distributed around the globe is normally sufficient to maintain a nominal uplink rate. But if a few ‘dishes’ are not usable for any reason, some of the satellites may receive ephemeris updates with significant delays. On such occasions, satellites would broadcast pre-computed extrapolated sets of ephemerides causing the age of ephemeris to grow as high as 3 hours.
Such periods occur few times a year and typically last 2-3 days. At the time of writing, the latest event of this kind happened March 5-7, 2021, while a previous one occurred January 19-20, 2021. Current updates as well as historical data are available from the unofficial Galileo monitoring site galmon.eu. According to the information on this site, the age of ephemeris never exceeds the value of 3 hours.
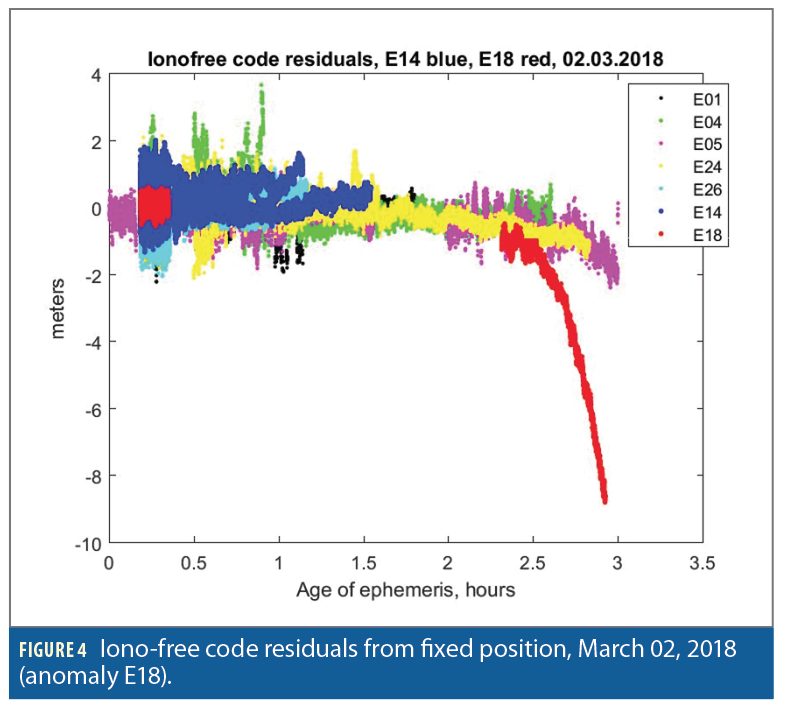
We used iono-free code residuals of standalone processing with a fixed position as indicators of anomalous orbit errors. Two examples are presented below: one case of historical data of March 02, 2018 (Figure 4) and a recent event of March 6, 2021 (Figure 5). Of course, code residuals include both orbit and clock errors, but it is well known than clock errors of E14 and E18 as well as of other Galileo satellites stay on submeter level and even decrease with the evolution of the system.
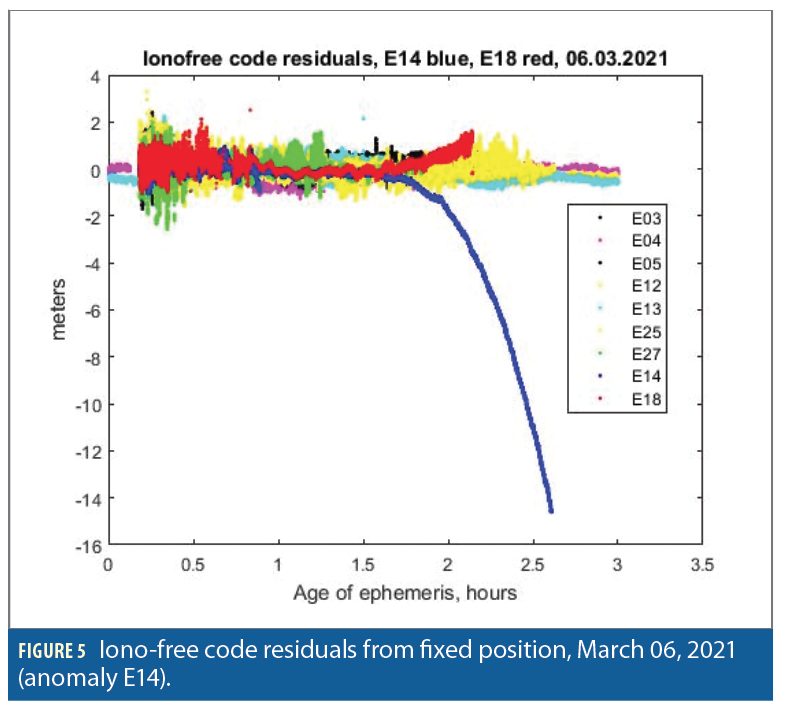
The RMS clock errors of Galileo satellites went down from 60 cm in 2015 to 25 cm in 2018. The behavior of both orbit and clock errors of E14 and E18 was analyzed in “Analysis of Galileo signal-in-space range error and posi- tioning performance during 2015–2018,” by W. Wu, W., Guo, F., Zheng, J., in Satellite Navigation, 1(6), (2020). It was clearly demonstrated that during the periods of orbit anomalies, clock errors remained at the same low level, no different from other satellites. This is logical: elliptical satellites differ from others in their orbits, not in their clocks. Hence, long-term meter-level anomalies of iono-free code residuals can be safely attributed to orbit errors.
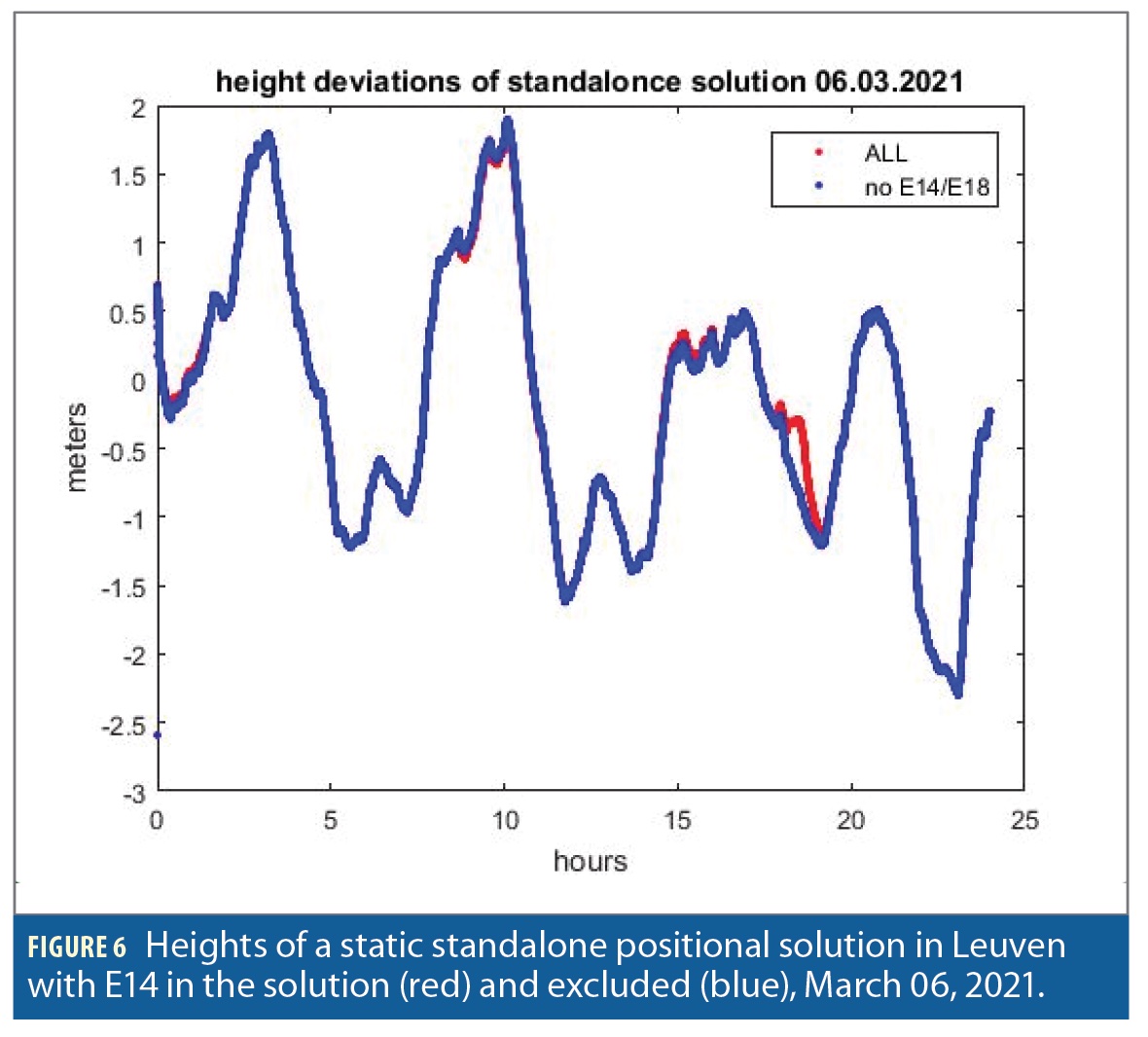
The impact of such orbit anomalies on quad-constellation GNSS (actual default in precise GNSS positioning) is small. Indeed, the total number of satellites used in open- sky applications is about 30 (34 in the case of Figure 6), hence the disturbance of the solution caused by a single satellite with high orbit error is visible but does not bring about what we would call ‘an outlier.’ The contribution of elliptical satellites is further reduced by the fact that Galileo observations are somewhat de-weighted relative to GPS observations.
Indeed, if Galileo and GPS ICDs are followed to the letter, Galileo satellites must be used with the variance of orbit errors of 9.43 m2, while for GPS the same value is 4 m2. This means that the impact of Galileo satellites would be attenuated relative to GPS.
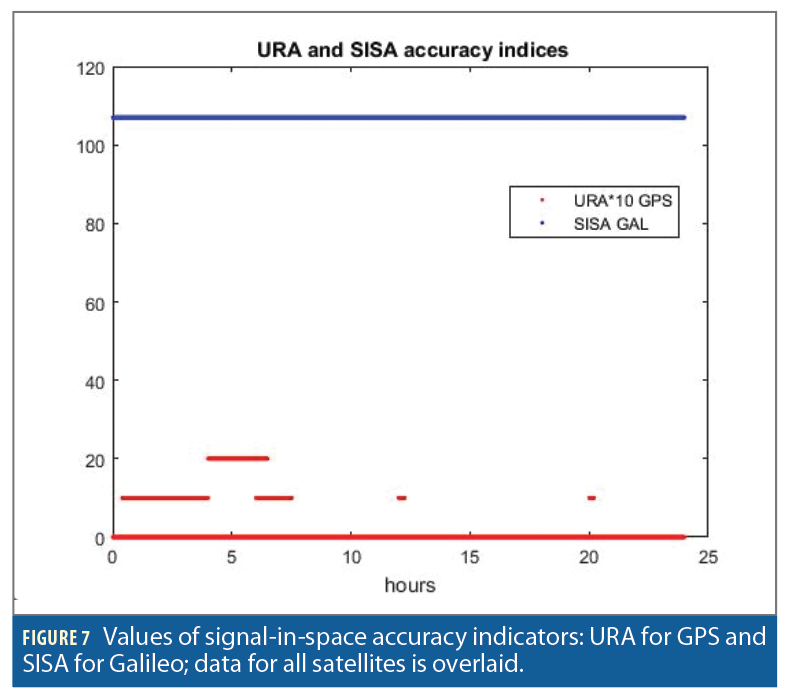
But even this impact can be reduced or avoided if the SISA index, which at this writing stays the same for all satellites (Figure 7), would be used to inform users about the chances of higher orbit errors for elliptical satellites or in other similar cases.
This means that the ground segment should be aware of the time of actual upload of an ephemeris and estimate the lowest boundary of the possible age of ephemeris in extrapolated sets as well as the consequent error level. If this were the case, user receivers could appropriately adapt their noise models, or even temporarily remove satellites from the solution if the SISA index would take a special value (as stipulated in the ICD) indicating the absence of valid ephemeris. Note that this would be done in a strict formal accordance with the ICD.
Of course, receivers can also take measures to de-weight or exclude elliptical satellites during periods of high radial orbit errors. For example, receiver-side algorithm can detect elliptical satellites by a high value of orbit eccentricity (0.162) and then look at the age of ephemeris data. But the goal is to strive for complete backwards compatibility for all Galileo-compatible receivers out in the field. It seems that all the instruments needed to reliably protect Galileo users from the impact of rare occurrences of high orbit errors are available.
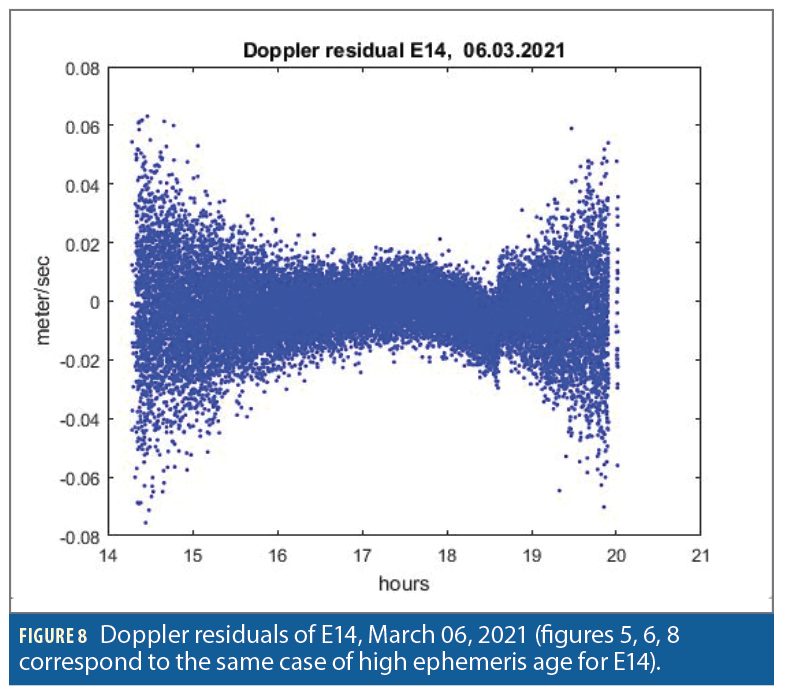
Radial velocities of elliptical satellites are shown in Figure 2; they reach the level of 600 m/sec. Nevertheless, residuals of Doppler measurements obtained at the computation of receiver’s velocity are but slightly biased (Figure 8).
The maximal impact, corresponding to the radial error of 15m is about 1cm/sec. Simple estimation shows that this error is caused by high values of the time derivative of radial orbit errors (15m/1800sec = 0.8 cm/sec). The jump in Doppler residuals corresponds to the moment when the ephemeris of E14 was finally updated; at this point a fresh ephemeris was received and a small bias was corrected. The impact of this bias on velocity calculation is insignificant.
Impact on RTK performance
Let us now turn to phase-differential RTK processing. Orbit errors enter RTK processing with an attenuation factor of the order of baseline/range. With a typical RTK baseline of approximately 10 km and normal radial orbit errors of about 1 m, their contribution to RTK error budget for heights would be less than 1mm. With an unrealistically high (in normal situations) radial orbit errors of 5m, the RTK height error would reach 3-5 mm.
The fact of a simple proportionality between the impact of orbit errors on standalone and RTK positioning means that if orbit errors are high enough to degrade RTK, they would degrade standalone positioning as well. Hence, the information on the expected values of orbit errors encoded in the SISA index can be used for both standalone and RTK error modeling.
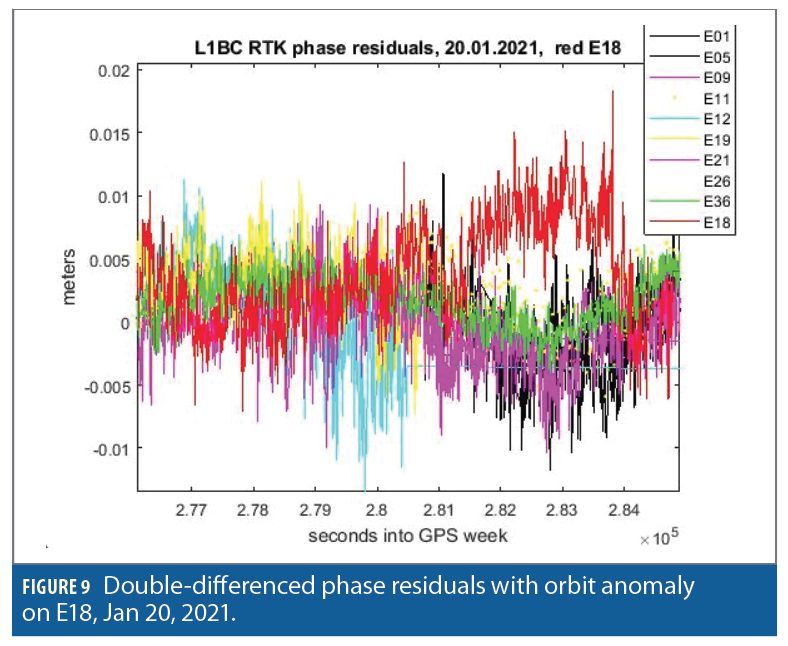
In fact, RTK is less sensitive to orbit errors than standalone positioning. Figure 9 shows double-differenced phase residual of E18 on Jan 20, 2021 when it had orbit errors of the order of 10 m. With the baseline of about 15 km, phase residuals reached the values of 1.5-2 cm. This kind of error is on the high side of the statistical distribution, but it might as well have occurred due to high multipath or for other reasons.
High radial speeds of satellites on elliptical orbits cause one more peculiarity in RTK computation. In the cases of high time latency between rover measurements and base station corrections, satellite’s positions and ECEF radii for base and rover epochs combined in RTK could differ significantly. This means that so-called ‘double differencing’ is not to be taken literally: one cannot just subtract base and rover measurements.
Satellite positions and relativity corrections must be accurately referred to transmit times on base and rover. Of course, the same is true for normal satellites as well, but for elliptical satellites the difference is significantly greater and a price of computational inaccuracy or an invalid approximation is higher. For example, when base station corrections are 10 seconds behind the rover measurements, relativity corrections on base and rover might differ by 30 cm.
To make sure that no extra errors would creep into RTK algorithms via time latency of corrections, we verified double-differenced phase residuals for E18 and E14 satellites when the time intervals of RTCM3 differential corrections were 1, 5, 10, 30 and 60 seconds. This experimentation has shown that the noise of phase residuals for elliptical satellites was growing with the delay of differential corrections at the same rate as for ordinary Galileo satellites, hence eccentric satellites did not present in this respect any anomaly at all.
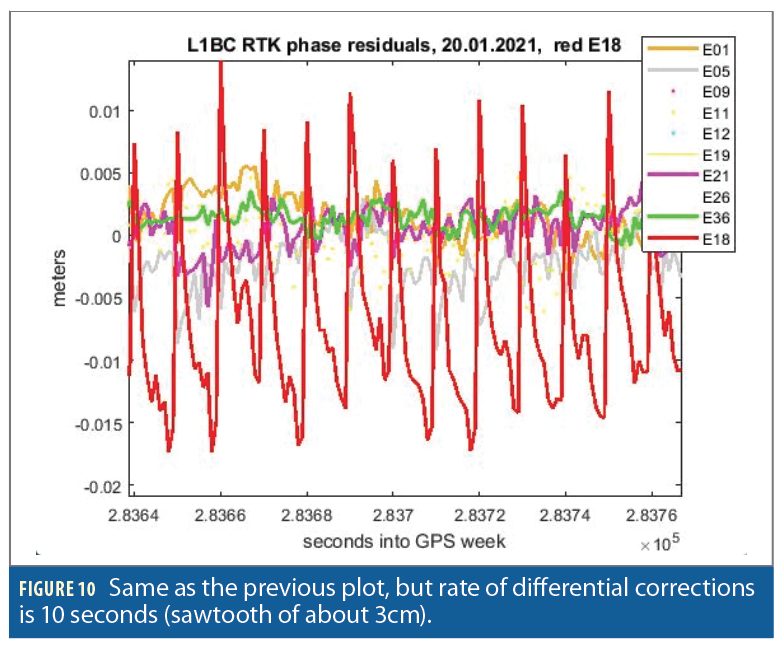
However, if anomalous orbit errors occur simultaneously with high time latency of differential corrections, a new kind of error would appear, which can reach values of about 10m/1hr = 3mm/sec. For example, with the time latency of 10 sec, the extra error would reach 3 cm for any baseline length. This means that if differential corrections would arrive at a rate of 10 seconds and if the radial orbital error of eccentric satellites would, at the same time, reach values of the order of 10m, phase residuals of these satellites would exhibit a sawtooth pattern with an amplitude of about 3 cm (Figure 10). The overall impact on RTK-computed positions in real-life applications will depend upon the availability of other satellites and multiple environmental factors.
Conclusions
Our analysis of precision-critical points in standard navigation algorithms has shown that elliptical satellites generally contribute to both phase-based and code-based positioning with no extra errors. However, with elliptical satellites there exists a chance of higher radial orbit errors of the order of ten meters on rare occasions when the age of ephemeris grows from nominal values of 20-30 minutes to 2.5-3 hours. This happens few times a year due to logistical problems and a limited uplink capacity of Galileo’s ground control segment.
The impact of these extra errors on standard RTK services with baselines of about 10 km was insignificant in our examples (as it is expected for normal benign cases). However, when differential corrections are received with a delay during such periods of abnormally high orbit errors, a peculiar cm-level bias in double-differenced measurements is generated. This baseline-independent bias is proportional both to the latency of corrections and to the time rate of radial orbit errors.
According to the ICD, Galileo users must be alerted about the possibility of high orbit errors by means of increased values of the SISA index (or a value indicating the absence of orbit prediction), which would prompt users to adapt their noise models or to remove a satellite from the solution. Hence, we conclude that there is no reason to declare E14 and E18 satellites unhealthy, but it is advisable to report appropriate values of the SISA index to indicate degraded accuracy of orbit predictions.
These conclusions are not directly applicable to PPP. With all the variety of existing PPP services and providers, the impact of elliptical orbits on the PPP performance may differ between providers.
Authors
Andrew Simsky received his Ph.D. in physics from the University of Moscow. He is currently involved with design and performance analysis of GNSS navigation algorithms.
Dries Schellekens received his M. Sc. in electrical engineering and Ph.D. in computer security and cryptography from the Katholieke Universiteit Leuven. He is an embedded software engineer at Septentrio.
The authors presented the material in this article at the ICL-GNSS2021 conference, Tampere, June 2021.