This research derives effective formulas relating GNSS meta-signal observations to the measurements obtained from its side-band components, when processed independently in a standard receiver architecture. Meta-signal processing can lead to high-accuracy solutions even under harsh conditions.
DANIELE BORIO AND CIRO GIOIA
EUROPEAN COMMISSION, JOINT RESEARCH CENTRE (JRC)
High-accuracy position, velocity and timing (PVT) solutions are key enablers for several applications including surveying, autonomous driving and precision farming, just to mention a few. High-accuracy PVT information is usually obtained using carrier-phase measurements in precise point positioning (PPP) or real-time kinematic (RTK) solutions, which operate well in favorable propagation conditions such as open-sky. Problems may, however, arise in harsh propagation conditions or long converge times may be required for filtering carrier-phase observations and achieving the full benefits of PPP and RTK solutions.
For this reason, significant research has been performed to obtain high-accuracy position solutions using code-only measurements. In this respect, GNSS meta-signal processing is a promising approach that can lead to high-accuracy solutions even under harsh conditions. Meta-signal processing exploits the full potential of modern GNSS, which broadcast several signals on different frequencies. Indeed, a meta-signal is obtained by jointly processing two (or more) components broadcast on two different frequencies as a single entity.
The resulting composite signal has a Gabor bandwidth much wider than that of the original signals denoted in the following as side-band components. A wide Gabor bandwidth is required to obtain high-accuracy pseudoranges and consequently high-accuracy code solutions. The concept of meta-signals was originally introduced by J. L. Issler et alia (see Additional Resources) and since then significant work has been performed to solve the challenges related to meta-signal processing and in particular, the code ambiguity problem. A recent article from J. A. García-Molina listed in additional resources describes a possible approach for effectively processing GNSS meta-signals and obtaining position solutions with a sub-meter accuracy.
While significant work has been performed in the signal processing domain, to design efficient methods for processing GNSS meta-signals, little research has been performed to characterize meta-signal carrier phases and pseudoranges. The goal of this article is to derive effective formulas, relating GNSS meta-signal observations to the measurements obtained from its side-band components, when processed independently in a standard receiver architecture. These formulas allow reconstruction of meta-signal observations from side-band measurements and shed light on the nature of meta-signal carrier phases and pseudoranges. Meta-signal pseudoranges, in particular, are obtained by mixing both code and carrier observations from the side-band components: thus they cannot be considered as pure code measurements. Ambiguities in meta-signal code observations can also be explained in terms of the ambiguities originating from the side-band carrier phases.
Meta-signal Processing
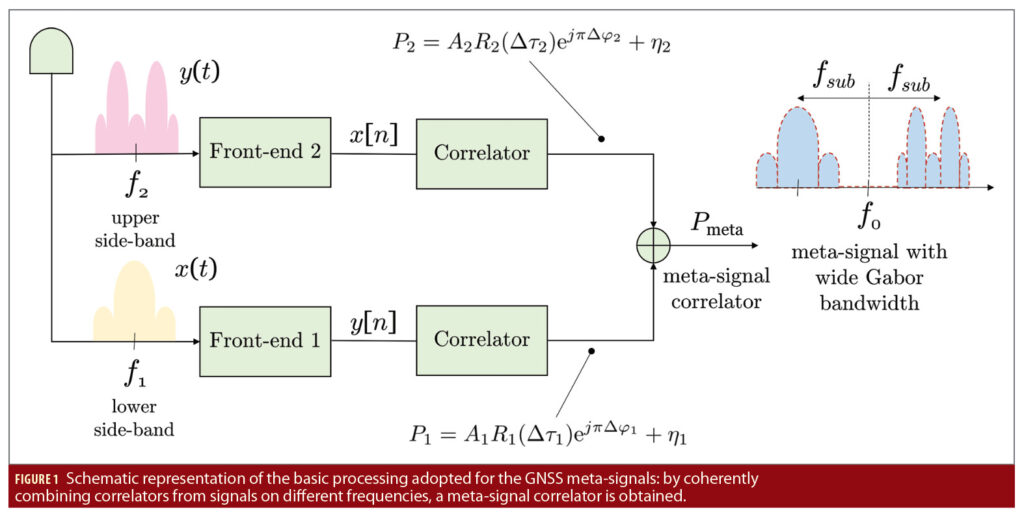
Meta-signals can be effectively processed by coherently combining the correlators obtained from side-band components. This fact has been demonstrated by the work of Paonni et al. listed in Additional Resources. Figure 1 provides a schematic representation of such processing, where two GNSS signals from the same satellite are recovered from different frequencies. The lower side-band component is denoted here as x(t) and has center frequency f1, whereas the upper side-band component is indicated as y(t) and has centre frequency f2. In Figure 1, two synchronous front-ends are used for the signal recovery, down-conversion, quantization and analog-to-digital conversion. The same operation can be performed using a wide-band front-end able to recover the whole band including both f1 and f2 frequencies.
After analog to digital conversion, the digital sequences obtained from the side-band components are correlated and a pair of complex correlators, P1 and P2 are obtained. When processed in an independent way, these correlators are a function of the side-band residual code delay and carrier-phase errors and can be expressed as:
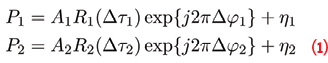
where Δτi and Δφi are the residual code and carrier-phase errors for component i = 1, 2. R1(.) and R2(.) denote the correlation functions of the side-band components with amplitudes A1 and A2, respectively. Finally, η1 and η2 are two independent noise terms. In Eq. (1), the effect of residual Doppler frequency errors has been neglected.
In meta-signal processing, the two side-band components are processed jointly, and constraints are imposed on the residual code and phase errors of the side-band components. For instance, a single code-delay error, Δτ1 = Δτ2 = Δτ0, may be tracked using a single delay lock loop (DLL), driven by a single meta-signal correlator obtained by coherently combining the side-band correlators, P1 and P2. In this work, we assume the use of a dual-phase estimator (DPE) architecture for tracking the meta-signal carrier-phase components. In particular, by coherently combining P1 and P2 and constraining Δτ1 = Δτ2 = Δτ0, the following correlator is found:
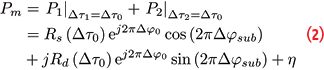
where Rs(Δτ0) = A1R1(Δτ0) + A2R2(Δτ0) and Rd(Δτ0) = A1R1(Δτ0)-A2R2(Δτ0). Δφ0 is the meta-signal residual carrier-phase error and Δφsub the residual subcarrier-phase error. In a DPE architecture, these components, further discussed in the next section, are tracked independently using two separate loops, which provide carrier and subcarrier measurements. The use of a dedicated loop to track the subcarrier phase solves the ambiguity problem that arises in meta-signal processing when side-band components are combined. When the subcarrier phase is assimilated to the code delay, the cosine term in Eq. (2) introduces secondary peaks in the meta-signal correlation function that becomes ambiguous: if a single tracking loop is adopted to track code and subcarrier components, false locks on secondary peaks can occur, leading to ambiguities in the code measurements. A DPE architecture, discussed in the relative article cited in Additional Resources, solves this issue.
Synthetic Measurements
By comparing the correlation functions obtained considering side-band processing, i.e. assuming separate residual code delay and carrier-phase errors for each side-band component, and the overall meta-signal correlation function with constrained errors, we were able to obtain formulas relating meta-signal pseudoranges and carrier phases to the side-band observations. Note that residual errors are estimated by the receiver tracking loops and used for the generation of the final observations. For this reason, it was possible to establish relationships between the different sets of measurements. In the following, final formulas are provided without proof. Additional details can be found in our paper listed in Additional Resources.
The meta-signal carrier-phase error, Δφ0, introduced in the previous section, is the average of the residual carrier-phase errors on the individual side-band components. This implies that the meta-signal carrier phase is the average of the side-band carrier phases expressed in cycles:
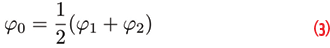
where φ1 and φ2 are the side-band phase measurements and φ0 is the meta-signal carrier phase. All the measurements are in cycles. Taking into account that the meta-signal center frequency is the average of the side-band center frequencies, carrier phases in meters can be expressed as
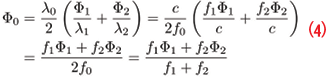
where f0 = ½(f1 + f2) is the meta-signal center frequency. λ1 and λ2 are the side-band signal wavelengths, λ0 the meta-signal wavelength and c the speed of light. Capital Φ letters are used to denote carrier-phase measurements in meters. Eq. (4) indicates that meta-signal carrier-phase observations are the narrow-lane dual-frequency combination of the side-band carrier phases. When Eq. (4) is used to reconstruct meta-signal phases directly from the side-band measurements, it is important to note that narrow-lane combinations are ambiguous of multiple integers of , the wavelength of the narrow-lane combination, which is half λ0. Thus, meta-signals can be reconstructed up to an integer number of λNL. When expressed in cycles, φ0 are affected by half-cycle ambiguities.
Similar to the carrier-phase case, it is possible to show that subcarrier-phase measurements in cycles are the mean differences of the side-band carrier phases:
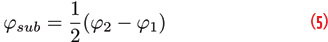
where φsub is the meta-signal subcarrier phase in cycle. When expressed in meters, the meta-signal subcarrier phase becomes the wide-lane dual-frequency combination of the side-band carrier phases:
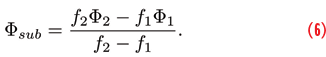
Similar to the previous case, the reconstructed meta-signal subcarrier phase is ambiguous of an integer number of wide-lane wavelengths, .
The reconstruction of meta-signal pseudoranges is more complex and requires two steps: the computation of the raw pseudoranges, derived from the code error, Δτ0, alone, and the final high-accuracy pseudoranges obtained combining raw pseudoranges and subcarrier phases. This last step is equivalent to the combining approach introduced by Hodgart et al. (2008) in the double estimator (DE).
Meta-signal raw pseudoranges can be reconstructed from the pseudoranges of the side-band components using the following relationship:
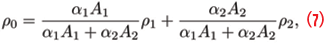
where A1 and A2 are the correlation amplitudes introduced above and α1 and α2 are the slopes of the main peak of the correlation functions, R1(.) and R2(.). The side-band pseudoranges are denoted as ρ1 and ρ2 whereas ρ0 is the raw meta-signal pseudorange. According to (7), ρ0 is a weighted average of the side-band pseudoranges: contributions from the signal with the sharpest correlation function and with the highest amplitude (or equivalently highest signal power) are weighted the most. If the two side-band components are received with the same amplitude and are characterized by the same modulation, (7) becomes a simple average:

The final meta-signal pseudoranges are obtained as
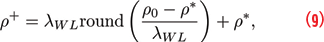
where “round(.)” is the rounding operator that returns the closest integer to its argument and ρ* is derived from the subcarrier phase as
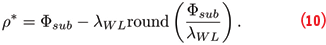
The improved accuracy of meta-signal pseudoranges is due to the subcarrier component that is determined by the carrier difference of the two side-band components. In this respect, meta-signal pseudoranges are mixed code and carrier measurements.
These formulas allow construction of synthetic meta-signal measurements from side-band observations.

Experimental Setup
To support these theoretical findings, experiments have been performed using real measurements collected using the receiver shown in the left part of Figure 2. This device can simultaneously process the Galileo Alt-BOC modulation and its side-band components, the E5a and E5b signals. In this way, we were able to simultaneously collect observations for the full Alt-BOC, which is considered a meta-signal, and its side-band components. Carrier smoothing was disabled to obtain pure code measurements. The receiver was connected to the rooftop antenna of the European Microwave Signature Laboratory (EMSL) of the European Commission Joint Research Centre (JRC). The right part of Figure 2 gives an aerial view of the JRC EMSL with the location of the multi-frequency GNSS antenna used for the experiment.
Experimental Results
The data collected using the experimental setup have been used to compare measurements from the Alt-BOC modulation with synthetic observations obtained from the E5a and E5b components.
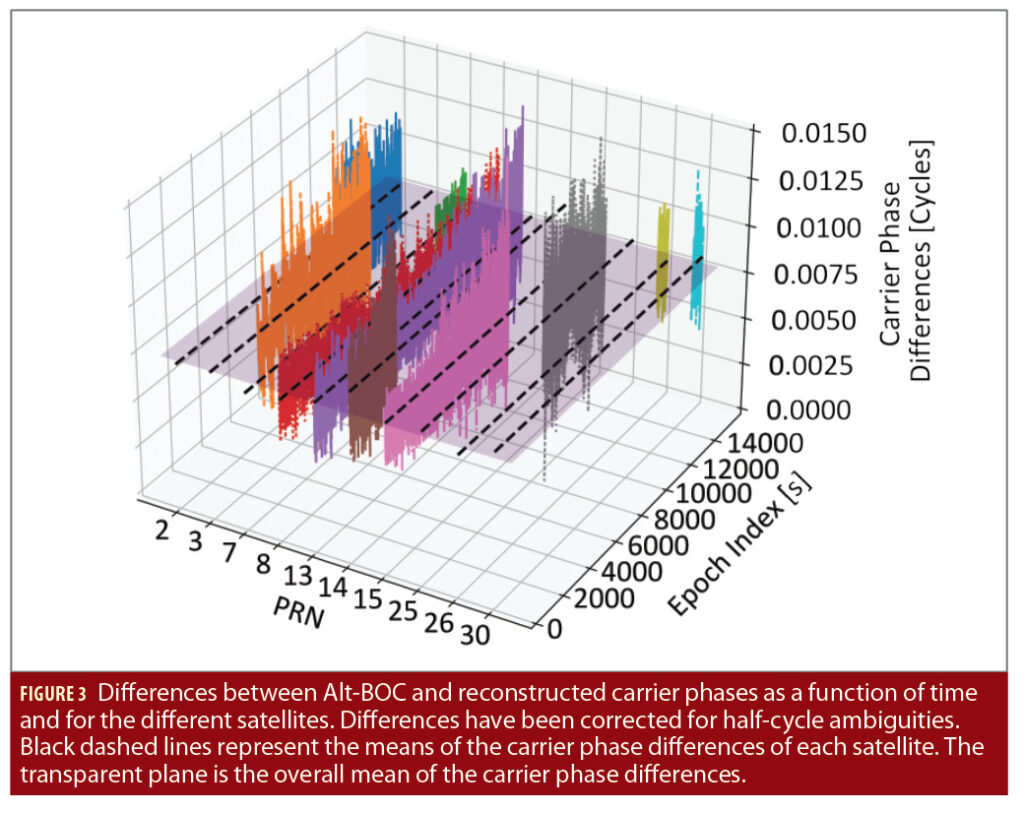
Differences between Alt-BOC and reconstructed carrier phases are depicted in Figure 3 as a function of time and for the different satellites. As discussed earlier, reconstructed carrier phases suffer half-cycle ambiguities due to the factor 1/2 in the reconstruction formula (see Eq. (3)). For this reason, the differences depicted in Figure 3 have been corrected for half-cycles that have been removed. Black dashed lines represent the means of the carrier-phase differences of each satellite: these means assume very close values and practically lay on the transparent plane, which represents the overall mean of the carrier-phase differences. In a position solution, these constant means affecting the carrier-phase differences will be absorbed in the clock bias. Carrier-phase differences are also affected by random variations around their means: these variations are reduced, and the associated overall standard deviation is 1.36 ·10-3 cycles (about 0.34 mm). This standard deviation and the associated variations are within the processing noise of carrier-phase observations.
Note that it is not possible to expect identical carrier phases from the Alt-BOC processing and from the recombination of E5a and E5b observations: the Alt-BOC and its side-band components are processed with different algorithms and possibly with different tracking loops. Thus, equivalence should be expected in an approximate statistical sense. The differences in Figure 3 confirm the validity of reconstruction formula (3) and that meta-signal carrier phases can be reconstructed from side-band observations up to an integer number of half-cycles and with a constant offset that will be absorbed in the clock-bias term of the final position solution.
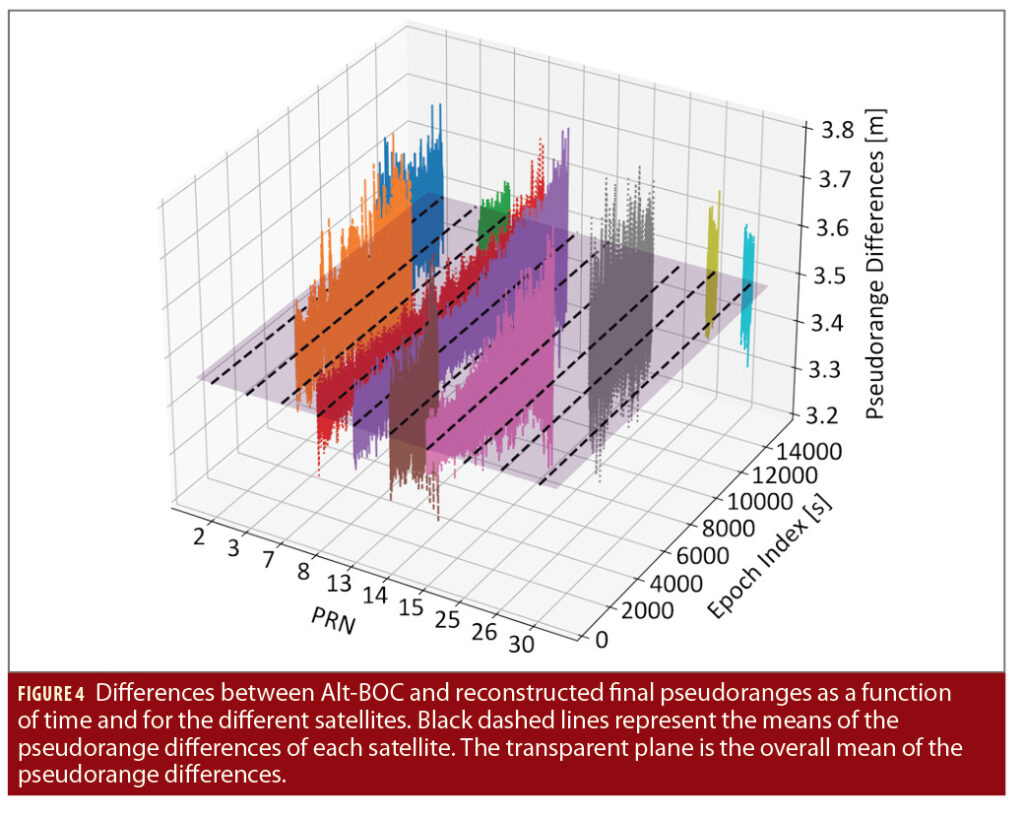
An analysis similar to that conducted for the carrier phase has been performed for the pseudoranges. Figure 4 shows the differences between Alt-BOC and reconstructed final pseudoranges as a function of time and for the different satellites. In this case, no ambiguity exists, and no correction has been applied to the pseudorange differences. Also in this case, the pseudorange differences have very close means (black dashed lines in Figure 4) that lay on the same plane. As for the carrier-phase case, these additional means will not impact the final position solution and will be absorbed by the clock-bias term. The pseudorange differences in Figure 4 are characterized by an overall standard deviation of about 5 centimeters. These results support the validity of Eq. (9) for reconstructing Alt-BOC pseudoranges from the code and carrier observations of the E5a and E5b components.
The pseudoranges from the E5a, E5b and the Alt-BOC signals have been used to compute different position solutions including those obtained from raw and final pseudoranges reconstructed from side-band observations. Figure 5 gives the scatter plots of the horizontal components of the different position solutions. Positions are displayed in an East North Up (ENU) frame centered around the true location of the EMSL roof-top antenna. In this way, deviations from the origin can also be interpreted as position errors in meters.
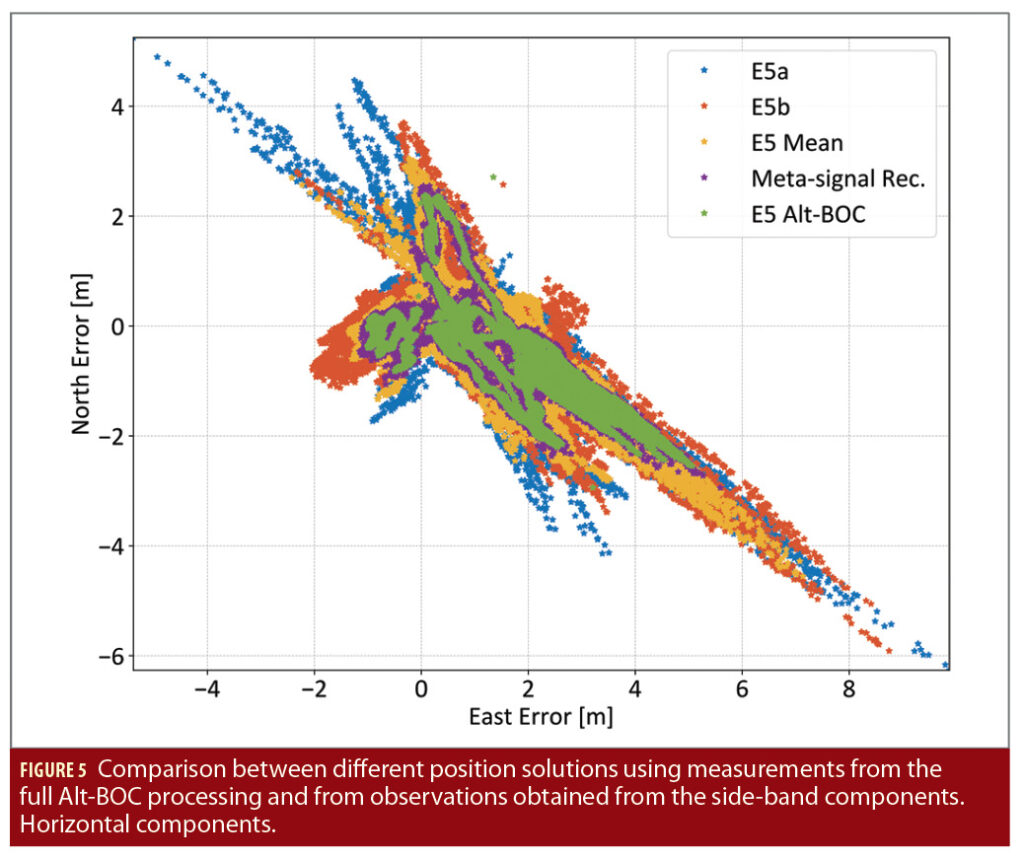
From the figure, it emerges that the most accurate position solution is the one obtained using Alt-BOC pseudoranges: the associated scatter plot in Figure 5 is the one with the lowest dispersion. The advantages of the Alt-BOC with respect to the E5a and E5b solutions clearly appear in Figure 5. When average raw pseudoranges are used, a reduction in the dispersion of the position solution scatter plot is observed with respect to the side-band components. However, the accuracy of the Alt-BOC solution is not reached. When reconstructed final pseudoranges are used, position solutions very close to those obtained using the Alt-BOC pseudoranges are found: this fact clearly emerges in Figure 5 where the two corresponding scatter plots practically overlap.
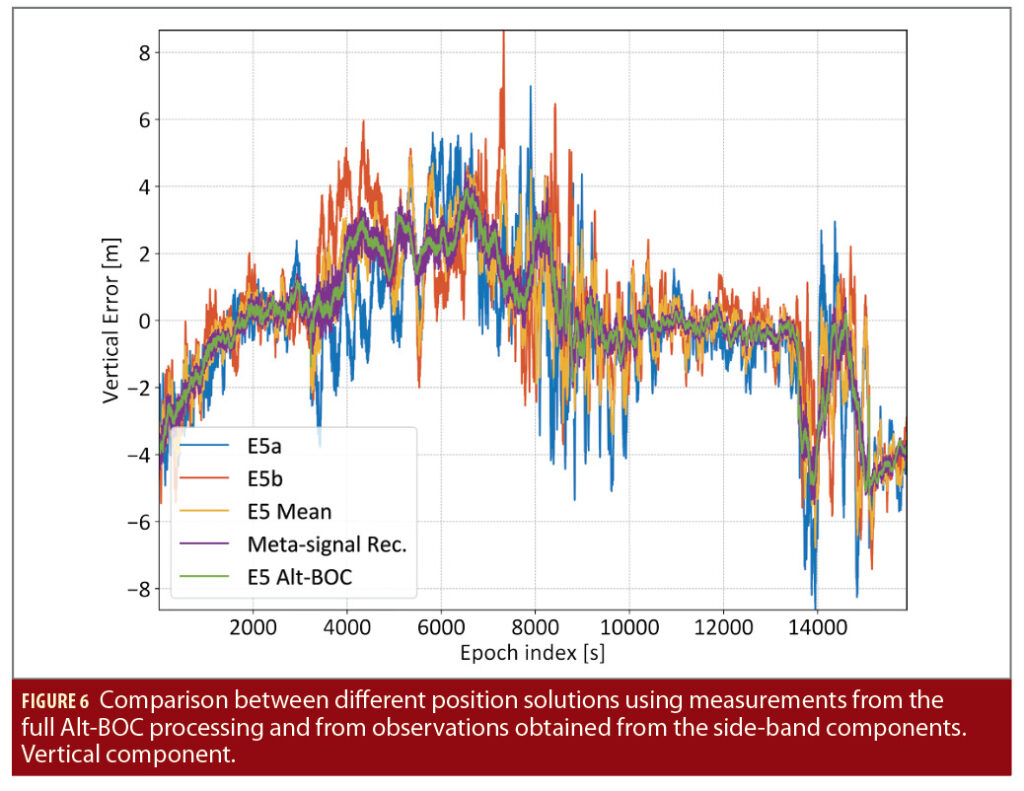
The vertical position errors for the different position solutions are shown in Figure 6: the vertical errors confirm the results discussed for the horizontal components. The Alt-BOC solution is the most accurate with clear advantages with respect to the side-band solutions. Also in this case, reconstructed final pseudoranges lead to position solutions very close to those obtained using Alt-BOC measurements. The vertical errors of the position solutions for the Alt-BOC and the reconstructed final measurements are practically coincident.
The differences between position solutions obtained using Alt-BOC and reconstructed final pseudoranges are zero mean and are characterized by random variations with a standard deviation lower than 25 cm, which is the value observed on the vertical component.
The results in the position domain further support the theory developed in the first part of this article: meta-signal measurements can be effectively reconstructed from the side-band observations.
Conclusions
Meta-signals observations can be effectively reconstructed from the pseudoranges and carrier phases of side-band components. When a DPE architecture is used for GNSS meta-signal processing, the meta-signal carrier phase is equal to the narrow-lane dual-frequency combination of the carrier phases of its side-band components. Similarly, the meta-signal subcarrier phase is equivalent to the
wide-lane combination of the side-band carrier phases. Finally, meta-signal high-accuracy pseudoranges are obtained by mixing side-band pseudoranges, averaged to reduce noise, and wide-lane combination of the side-band carrier observations. In this respect, meta-signal pseudoranges are not pure code measurements but take advantage of the subcarrier component that is used to smooth the final code observations.
Manufacturers
The multi-frequency multi-constellation GNSS receiver used for the data collection is a PolarRx5S device from Septentrio.
Additional Resources
(1) Borio D., “Double Phase Estimator Towards a New Perception of the Subcarrier Component”, Inside GNSS, May/June 2015, pp. 58-64
(2) Borio D. and Gioia C. “GNSS Meta-signals, Dual-frequency Combinations and the Double Phase Estimator”. In Proc. of the Institute Of Navigation (ION) International Technical Meeting (ITM), January 2022, pp. 1-12.
(3) García-Molina J. A. “Unambiguous Meta-Signal Processing a Path to Code-Based High-Accuracy PNT”, Inside GNSS, March/April 2021, pp. 50-55
(4) Hodgart M. S., Blunt P. D. and M. Unwin “Double Estimator a New Receiver Principle for Tracking BOC Signals”, Inside GNSS, Spring 2008, pp. 26-36
(5) Issler J.-L., Paonni M. and Eissfeller B. “Toward centimetric positioning thanks to L- and S-band GNSS and to meta-GNSS signals”. In Proc. of the ESA workshop on satellite navigation technologies and european workshop on GNSS signals and signal processing (NAVITEC), December 2010, pp. 1-8
(6) Paonni M., Curran J., Bavaro M., and Fortuny-Guasch, J. “GNSS meta signals: Coherently composite processing of multiple GNSS signals”. In Proc. of the 27th International Technical Meeting of the Satellite Division of the Institute Of Navigation (ION GNSS+), September 2014, pp. 2592-2601.
Authors
Daniele Borio received a doctoral degree in electrical engineering from Politecnico di Torino. Previously a senior research associate in the PLAN group of the University of Calgary, Canada, he is currently a scientific policy officer at the European Commission (EC) Joint Research Centre in the fields of digital and wireless communications, location and navigation.
Ciro Gioia received an MSc. in Nautical Sciences and a Ph.D. from Parthenope University. After serving as an external consultant at JRC, he is now scientific project officer at the center, focusing on location and navigation with special emphasis on geomatics aspects.