In the past two decades, satellite navigation systems have undergone great development. The development of new generations of global navigation satellite systems (GNSS), represented by GPS III, Galileo, and the BeiDou global system (BDS), is rapidly advancing.
Signal design is one of the core tasks of GNSS development, because the broadcast signal is the only interface of the system for receivers, and its inherent performance determines the success of the entire system’s performance. Once the signal detail is defined, any subsequent change may cause changes to a large number of user terminals, which could have significant cost impact.
Therefore, GNSS signal design cannot simply follow the “release first, update later” route. It must be fully studied and demonstrated before system implementation. However, as a significant infrastructure, GNSS has a long development cycle. It may take several years from the time of initial signal design to the full operation of the system. This fact forces signal designers to have sufficient foresight, using existing technology, to enable unknown service requirements over future decades of operation. Therefore, although most of the signals in current GNSS have been defined, the evolution of GNSS signal design will not stop there. The full operation of the current GNSS is the beginning of the design work of the next generation GNSS.
From the reality of GNSS design one can find that the growing expanded applications and refined services prompt the new generation systems to broadcast more signals with more complicated structure, which on the one hand makes more efficient use of limited spectrum resources, already crowded with GNSS signals, but on the other hand makes the spectrum crowding situation even worse. Moreover, such a complicated signal structure may make the realization of signal multiplexing more difficult for satellite payloads. Additionally, the limitation of receiving complexity, the requirement for backward compatibility, as well as the demand of interoperability among systems, add many constraints into the GNSS signal design optimization problem. The immaturity of methodology and the conflict between application expansions and resource scarcity cause the signal design of the next generation GNSS to face a series of challenges. At present, it is necessary to take a hard look at the technical challenges in future GNSS signal design, and look for possible solutions in advance.

Challenges Facing Future GNSS Signal Design
Compared with wireless communication signal design, the major feature of navigation signal design is the pursuit of high accuracy ranging capability. If we compare the wireless communication signal, of which the most concerned targets are the capacity and reliability of data transmission, to a paper envelope, then the satellite navigation signal can be compared to a ruler, since its main concern is the accuracy and robustness of the ranging measurement.
In the design process of this “ruler”, the selection of the carrier frequency, the optimization of the spreading modulation, and the multiplexing of signal components are the top three critical and challenging parts.
Carrier Frequency Selection
The carrier frequency, as is the material of a ruler, determines many of the attributes of a navigation signal, including the propagation characteristics, the cost of transmitting and receiving hardware, signal Doppler shift, and possible interference with other radio systems.
Among all available spectrum resources, the L-band has many advantages for satellite navigation applications, such as good propagation characteristics, moderate antenna size, and relatively small atmosphere influence, and therefore became the preferred frequency band for satellite navigation signals. At present, the vast majority of GNSS signals are gathered in the upper L band (1559 ~ 1610 MHz) and the lower L band (1164 ~ 1300 MHz).
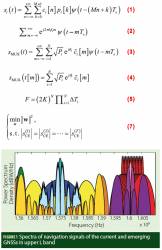
Figure 1 (see inset photo, above right) illustrates spectra of navigation signals of the current and emerging GNSSs in the upper L band. Obviously, it is hard to find any unoccupied contiguous segment in this frequency band. There are only a few scattered available frequency fragments remaining between main lobes of existing signals. Interference arises among different signals. Although it is possible to reduce the spectral overlap of the signal located at the same central frequency to a certain extent by using different subcarriers or adjusting the spreading chip waveforms, it is still becoming increasingly difficult to find a suitable central frequency for a newly added navigation signal in L-band.
Some studies (including Avila-Rodriguez et alia, and Irsigler et alia, Additional Resources) consider the use of higher frequency bands, such as the S-band at 2483.5 to 2500 MHz and the C-band at 5010 to 5030 MHz. However, compared with L-band, the valid frequency spectrum allocated to navigation service in S- and C-bands is more limited, so that signals these bands can support are more limited. In addition, using these bands with higher frequencies will result in greater space transmission loss, greater phase noise, and greater Doppler shift.
Spreading Modulation Design
Spreading modulation is to a satellite navigation what scale is to a ruler. The most direct influence of the spreading modulation design is to adjust the signal spectrum shape in order to distribute the power of the signal to a specific frequency position. Research indicates that spreading modulation directly affects the receiving performance for a signal in thermal noise, interference, as well as multipath environments, and RF compatibility between signals in the same frequency band. Therefore, the optimization of the spreading modulation technique is considered one of the most important ways to realize spectrum compatibility and performance improvement simultaneously.
In the new generation GNSS, there are two new trends emerging in spread modulation design. Firstly, signal power distribution is changing from concentrating near the carrier frequency to a splitting spectrum form, which is represented by binary offset carrier (BOC) modulation. Research indicates that splitting spectrum characteristics result in a spectrum separation from legacy signals located at the same central frequency and a wide root mean square (RMS) bandwidth which results in the potential advantage of improved ranging accuracy and inherent multipath resisting ability. Secondly, in addition to bipolar waveforms, more and more multi-level spread modulation waveforms are emerging, such as that in Composite BOC (CBOC) and Alternative BOC (AltBOC) modulations. Relaxing the constraint of waveform level can provide greater freedom for spread modulation waveform optimization, thus providing more possibilities for improvement of the signal performance (Pratt and Owen, and Zhang et alia 2011, Additional Resources).
However, these two trends bring increased complexity to both the transmitter and the receiver. The larger RMS bandwidth of the splitting spectrum signal requires a higher subcarrier frequency, which means a wider receiver frontend bandwidth and the increment of complexity of the receiver. Although the sophisticated receiving strategy is acceptable for high-end applications such as surveying and mapping, the cost and complexity is hard to justify for low-end consumer electronics devices. A direct way to address this problem is by transmitting multiple signals from the satellite, providing high-end users with a wideband signal that uses a complex chip waveform, while allowing the low-end users to have a simple receiving strategy for a narrowband signal with a simple chip waveform. Unfortunately, the increment in the number of signals at the same frequency degrades the multi-access interference (MAI) between the system and the inter-system signals, which leads to deterioration in the receiving performance. Furthermore, the increase in the number of signals and the complexity of the signal waveform pose a challenge to constant envelope multiplexing, which is another critical part of satellite navigation signal design.
Multiplexing
Signal multiplexing refers to the technique of combining multiple different signal components into one signal over a shared transmitting chain. It is not widely treated in most GNSS interface control documents (ICDs) but is the basis for a variety of PNT services for today and the future. Due to the limitation in GNSS transmitting power and the nonlinearity of the amplifier, multiple spreading signals should share a carrier frequency and multiplex into a composite signal with a constant envelope in the signal transmitter.
In the constant envelope multiplexing on the navigation satellite, as the number of multiplexing signals increases, more inter-modulation terms power should be added to keep the envelope of multiplexed signal constant. Since the information carried on inter-modulation terms is redundant for a receiver, the higher proportion of inter-modulation terms mean the less useful power output, which is expressed as a lower multiplexing efficiency, thus reducing the received carrier to noise ratio (CNR). Though increasing the transmitting power can compensate for the multiplexing loss, it will further deteriorate MAI between the system and the inter-system signals.
A Gordian Knot
Under the conventional idea of separately optimizing carrier frequency, spreading modulation, and multiplexing, a Gordian knot is emerging in future GNSS signal design. As shown in Figure 2, in the independent design of these three key elements, it is difficult to reconcile the contradictions among service diversity, ranging accuracy, receiving complexity, radio frequency (RF) compatibility and multiplexing efficiency.
Users always want signal ranging performance to be as high as possible while the receiving complexity is as low as possible. However, one cannot have both at the same time. The most straightforward way to cope with the high-performance demand is to increase the signal bandwidth, and moving the main spectrum component of signal away from the carrier frequency. However, since there are almost no contiguous segments of unoccupied spectrum remaining in the upper L-band, increasing the signal bandwidth will aggravate spectral interference between the new signal and existing signals. Furthermore, a wider signal bandwidth and complex subcarrier structure also result in a higher processing burden on receivers, which is unacceptable by low-end users. The direct way to further support low-end users is to add more narrowband signals with simple structures. Nevertheless, increasing signal numbers not only further increases spectrum interference, but also further reduces the power efficiency of multiplexing. That means the useful signal power is reduced, and also that the interference is increased. As a result, although the original intention is to improve the overall performance, the actual effect is to degrade the performance of each signal component.
In order to get out of the cycle of contradictions among measurement accuracy, services variety, RF compatibility, as well as multiplexing efficiency in satellite navigation signal design, it is necessary to break the routine.
Our inspiration is attributed to Vernier caliper, which combines two rulers with different scales together. In principle, each scale can be used independently as a simple ruler. However, based on the difference between scale divisions of these two rulers, when we use these two scales jointly in a proper way, we can obtain a higher measurement accuracy. Along the way, in navigation signal design, when we re-examine carrier frequency, spreading modulation, and multiplexing these three key elements as a whole, we find a solution to cut the Gordian knot: the multicarrier constant-envelope composite (MCC) signal.
Multicarrier Constant-Envelope Composite Signal
The concept of multi-carrier signals originates from the field of wireless communications. Typical multicarrier communication signals include multi-tone signals, orthogonal frequency division multiplexing (OFDM) signals, and multicarrier code division multiple access (MC-CDMA) signals. However, the satellite navigation signal has two major differences compared with the communication signal: First, the core mission of the navigation signal is the high accuracy time of arrival (TOA) estimation but not the data transmission. The TOA estimation processes based on multi-carrier communication signals, such as OFDM signal, are complex (See Thevenon et alia, Additional Resources) and the inherent high RMS bandwidth performance advantage of multi-carrier signals is difficult to be adequately brought into play. Second, the vast majority of existing multi-carrier signals have a high peak-to-average ratio (PAR), which hinders their application for satellite transmission (See Mateu et alia, and Emmanuele et alia, Additional Resources).
Unlike the above-mentioned multicarrier communication signals, as shown in Figure 3, the proposed MCC signal is like a “spectral transparent adhesive”. It “glues” a plurality of narrowband signal components located in multiple spectral gaps together to form a wideband constant envelope signal, sharing a common up-converter, amplifier chain and antenna aperture. The core features of the MCC signal are:
- Sparsity in the frequency domain;
- Envelope constancy in the time domain;
- High flexibility on design elements such as the number of sub-bands, sub-band frequency spacing, the number of signal components in each sub-band, shape of the spreading waveform, the power ratio and relative phase of signal components;
- Transparency of the compositing to the receiver.
Compared with existing solutions, the MCC signal has the following unique advantages:
On the one hand, multicarrier is one of the most effective ways to utilize spectrum gap resources. As previously mentioned, in the increasingly crowded satellite navigation band, the absolute bandwidth of the newly added signal is severely limited. There are only some scattered frequency fragments available between main lobes of existing signals, as illustrated in Figure 3(a). However, the frequency difference between signal components in different sub-bands of the multi-carrier signal can transform this unfavorable factor into a favorable one. As illustrated in Figure 3(b) and (c), placing multiple sets of narrowband signals components in the fragment band gaps and combining them into a wideband constant envelope signal can construct a MCC signal. The spectrum sparse characteristic of such signal can not only ensure adequate spectral separation with existing signals in the same band, but also provide a large RMS bandwidth for better ranging performance, resulting in solving the contradiction between spectral efficiency and ranging performance.
On the other hand, the different narrowband components in the MCC signal can be optimized for targeted PNT services, with different spreading sequences, different spreading waveforms, different power allocations, and different data message structures and contents, to meet future diversified PNT requirements. At the same time, in MCC signals, those components are combined into a whole signal by constant envelope multiplexing that is “transparent” enough for receivers, not only allowing narrowband receivers to process each component separately with low-complexity, but also allowing wideband receivers to process the total or partial components of this signal with a wide RMS bandwidth. That is, the MCC signal has innate features of diversified receiving and processing strategies, which addresses the contradiction between power efficiency and service diversity.
In addition, the integrated structure of the MCC signal ensures a strong correlation between the transmission channel effects of each sub-band component, which creates conditions for joint processing of components in multi sub-bands, such as joint acquisition, joint tracking, and joint pseudorange extraction.
Given the above, a MCC signal can not only achieve outstanding ranging accuracy without significantly increasing the RF interference to the existing signals in the same band, but also provide users with diversified and targeted service without noticeably deteriorating the multiplexing efficiency onboard the satellite. It provides a promising technique solution for the next generation GNSS signal design.
Construction of a MCC Signal Based on the CEMIC Method
The key to the MCC is determining how to combine several flexible signals located at multiple different central frequencies with arbitrary power, chip rate, and spreading waveform into an integral signal with a constant envelope. In the field of satellite navigation signal design, the study of constant envelope multiplexing has long focused at single-frequency cases. Although there are some dual-frequency constant envelope multiplexing methods, such as those described by Lestarquit et alia, Yao et alia 2016 and Zhang in Additional Resources, few of them can support multiplexing for more than two sub-bands. Moreover, the vast majority of existing constant envelope multiplexing techniques are only applicable under strict pre-conditions in the component waveform shape, component number, component power ratio and phase relationship, which is not suitable for the proposed conception of using multiple spectral gaps to carry diversified services.
The recent emergence of a high efficiency generalized multicarrier joint CEM technique for multilevel spreading signals, termed CEM via intermodulation construction (CEMIC), as described by Yao et alia 2017a in Additional Resources, presents the possibility for the realization of a MCC signal. Compared with existing CEM techniques, CEMIC has a much higher design flexibility in the number of sub-bands, the number of signal components, power ratio and phase relationship among components, and the shape of spreading chip waveforms. CEMIC can be applied to any number of bipolar or multilevel spreading spectrum signals with arbitrary power distribution at one or more subcarrier frequencies. Such a high degree of design flexibility provides system designers great room in signal scheme optimization for varied navigation applications in the future.
In this section, based on the design theories presented in Yao et alia 2017a, and Yao et alia 2017b, Additional Resources, an implementation technique of MCC with extremely high design flexibility is presented.
Consider combining N spreading spectrum signal components located at several sub-bands, si(t), for i = 1 = N , into a composite signal with constant envelope. In principle, there is no constraint on the spreading code rate and spreading waveform shape for each si(t). However, for simplicity, here we assume that all of the si(t) are MCS signals with the same code rate Tc, and every MCS symbol is divided into M segments with equal length Ts = Tc/M. More general cases can be found again in Yao et alia 2017. Then can be mathematically expressed as
Equation (1) (see inset photo, above righ, for all equations)
where ci is the navigation data modulated by the corresponding spreading code, pi is the waveform value in k-th segment, and ψ(t) is unit amplitude rectangular pulse function with Ts duration.
Define fi as the frequency offset of the subcarrier of si(t) from the carrier frequency f0, the selection of which depends on the specific location of spectral gaps. For the convenience of digital implementation, the subcarrier waveform can choose the sample-and-hold version of the complex sinusoid waveform
Equation (2)
where Δfi = fiTs. Since for all of the deployed GNSS signals, the carrier frequency, the spreading chip rate, as well as the subcarrier rate are all the multiple of 1.023 megahertz, by choosing the proper values of Tc, fi, and M, it is easy to ensure that ΔTi = 1 / Δfi is an integer. That means the signal component modulated by the subcarrier is still a MCS signal.
Directly combining these N signal components into a multicarrier composite signal is mathematically equivalent to constructing a new baseband signal, of which the complex envelope is
Equation (3)
where c̃i[m] = ci[n]pi[k] ej2πΔfim with n = [m Ts/Tc] and, k = [(mTs − nTc)/Ts], Pi and θi are the power allocation and initial phase of i-th component respectively.
It can be seen from the above equation that sMUX(t) is also a MCS signal with segment length Ts, and in every duration t[m] ∈ [mTs,(m+1)Ts) , its value is fixed to
Equation (4)
In general, the MCS waveform may have multi amplitude levels. For simplicity, assume that every pi has up to K different possible values, while every sample-and-hold version subcarrier waveform has up to ΔTi different values. Then sMUX(t) has a maximum of
Equation (5)
possible complex values, resulting in the temporal fluctuation of the envelope. In order to keep the envelope of the multicarrier composite signal constant, the basic idea of CEMIC is adding an additional component IIM(t) to sMUX(t) to compensate for the envelope fluctuation. This additional component can be referred to as the intermodulation (IM) term. In every time period t[m] ∈ [mTs, (m+1)Ts], the value of IIM(t) is determined by the value of sMUX(t[m]), to ensure the composite signal sCE(t) = sMUX(t) + IIM(t) is a constant envelope signal. As pointed out in Yao et alia 2012, this is equivalent to finding an amplitude mapping rule f: {c̃1, c̃2, …, c̃N} ↦ IIM, that gives values to the IM term for each of the F combinations of values of c̃i, to make the envelope of the superposed signal be constant.
If only the envelope constancy of sCE is constrained, then an infinite number of mapping rules can be used. However, since the IM term IIM(t) is only used to maintain the constancy of signal envelope, from a receiving power efficiency standpoint, its proportion should be as low as possible in the whole composite signal, and its influence on receiving performance should be as small as possible. The core of CEMIC is to find an optimal mapping rule, which constructs an IM term that can guarantee the optimal power efficiency, minimal impact on the correlation characteristics of useful components, and the envelope constancy of the composite signal.
Generally, using CEMIC to construct a MCC signal has the following four main steps:
1) According to Tc, fi, M, and the shapes of pi, for i = 1 = N, list all F possible combinations of values of {c̃1, c̃2, …, c̃N}, and construct the component weight vectors
c̃i = [c̃i(1), c̃i(2), …, c̃i(F)]T (6)
for i = 1 = N, where c̃i(ℓ) is the value of c̃i in the ℓ-th combination. Note that, in order to distinguish from the time index that is in square brackets, here the combination index is put in parentheses.
2) Based on component weight vectors c̃1, c̃2, …, c̃N using the Gram-Schmidt orthogonalizing method or other methods, construct a set of orthogonal vectors {g1, g2, …, gF-N} to make span{g1, g2, …, gF-N} be the orthogonal complement space of {c̃1, c̃2, …, c̃N}. A general construction algorithm for this step is given in Appendix A of Yao et alia 2017. However, if all of pi are bipolar, a much simpler direct construction method proposed in Zhang et alia 2012, Additional Resources can also be available.
Define
sCE = Cr + Gw, where C = [c̃1, c̃2, …, c̃N], G = [g1, g2, …, gF-N], and r = [√P1ejθ1, √P2ejθ2, …, √PNejθN]T and solve the following constraint minimization problem
Equation (7)
to obtain the optimal coefficient vector w, where s(ℓ)CE is the ℓ-th entry of sCE.
Let λ = Gw = [λ(1), λ(2), …, λ(F)]T. Then we obtain the optimal mapping rule from the value combination of N signal components to the IM term IIM(t). In every moment, if the values of {c̃1, c̃2, …, c̃N(t)} correspond to the ℓ-th value combination, IIM(t) takes the value λ(F), and sCE(t) = sMUX(t) + IIM(t).
Case Study of Adding a MCC Signal in L1 Band
As a sample application, consider adding a new MCC signal in the L1 band. Although current GNSSs do not have such a plan yet, through this specific example, one can clearly see the design process of a MCC signal, and the characteristics and advantages of this signal in both the transmitter and receiver.
As mentioned, the upper L-band has been overcrowded. All GNSSs broadcast their open and authorized service signals in this band. If a new wideband signal is added to this band, it will be hard to avoid significant spectrum overlapping with the existing signals. However, it is noted that most of the existing signals in this band have spectral nulls at 1575.42, ±4.092, ±8.184, and ±10.23 megahertz, etc. Thus, under the premise of ensuring good RF compatibility, a possible new signal solution is to place multiple narrowband components in these spectral gaps.
For simplicity, consider the case of multiplexing five narrowband components with BPSK-R(0.5) spreading modulation in this example. As shown in Figure 4, the center frequencies of these five components are set to 1577.466 MHz, 1579.512 MHz, 1581.558 MHz, 1583.604 MHz, and 1585.65 MHz, respectively. In the transmitter, the carrier frequency of the composite MCC signal can be 1581.558 MHz. Thus, the subcarrier frequencies of components are f1 = –4.092 MHz, f2 = –2.046 MHz, f3 = 0, f4 = 2.046 MHz, and f5 = 4.092 MHz, respectively. Under the equal power assumption, r can be set to [1,1,1,1,1]T. In this design case, considering the constraint of implementation complexity, M should not be too large. Here we take M = 8, the shortest segment length Ts = (32 °— 1.023e6)–1 s.
The theoretical power spectral density (PSD) of these five narrowband components before the constant envelope reconstruction is shown in Figure 5(a). Following four steps of the CEMIC method presented in the previous section, the MCC signal is constructed, for which the theoretical and simulation PSDs are shown in Figure 5(b) and (c), respectively.
By comparing Figure 5(a) and (b), it is observed that after constant envelope reconstruction, the PSD of the MCC signal is different from that of the direct superposition of these five components. The difference is mainly reflected in the appearance of the IM term in MCC signal. It can be seen that the power of the IM term is much lower than that of the useful signal components, and the difference is at least 10 decibels. In fact, the multiplexing efficiency of this example is 80.41%. That is, the newly added IM term accounts for only 19.6% of the total signal power, and its spectrum is distributed far away from the carrier center frequency.
Figure 6 shows the modulation constellation of the MCC signal. As illustrated in the figure, all the phase points are distributed on a circle. This feature enables the payload high power amplifier (HPA) to operate in its full-saturation mode to maximize power conversion efficiency.
RF Compatibility Analysis
To evaluate the RF compatibility between the newly added MCC signal and the existing BPSK-R(1), MBOC(6,1,1/11), BPSK (10), as well as BOC (10,5) signals in the same frequency band, we calculate their spectral separation coefficient (SSC). The receiver front-end filter is assumed to center on 1575.42 MHz, with a single side bandwidth of 12 megahertz, which is sufficient to cover the highest frequency component of the MCC signal. Table 1 shows the SSC of the existing signals with MCC signal.
It can be seen that the MCC signal maintains good RF compatibility with the existing signals by effectively utilizing the fragment band gaps between the main lobes of existing signal spectrum. It can be verified that if more sub-bands are employed, or moving f5 from 1575.42 + 10.23 MHz to 1575.42 + 12.276 MHz, the RF compatibility between MCC signal and the BOC(10,5) signal can be further improved.
Diversified Processing Strategies
As previously mentioned, in addition to the effective utilization of the spectrum resource, another key advantage of the MCC signal is that it inherently has multiple receive modes, providing a variety of processing strategies for receivers with different performance and complexity constraints.
Since the MCC signal is composited in the digital baseband, the subcarrier phase of each component is completely coherent, and components within the MCC signal pass through the same transmission channel, the errors introduced by thermal noise, multipath, as well as the dynamic stress also have strong correlation. The receiver can either treat these signal components separately, or jointly process multiple components or even the entire composite signal as a whole.
The simplest processing mode is treating the narrowband components in the MCC signal as different signals. Such a processing mode requires minimal processing complexity. If narrowband components employ BPSK-R spreading modulation, as discussed in this example, their acquisition and tracking methods can be directly inherited from the traditional cases, where both the rectangular pulse spreading chip and the sinusoidal subcarrier waveforms can be employed in the local replica. The cross-correlation function (CCF) between the received MCC signal and the local replica of each signal component in this processing mode is shown in Figure 7(a).
If the receiver jointly processes three signal components, which are s2(t), s3(t), and s4(t), without loss of generality, the local replica can be
slocal(t) = s2(t)ej2Πf2t + s3(t) + s4(t)ej2Πf4t (8)
The CCF between the received MCC signal and this local replica is shown in Figure7(b).
Further, the whole MCC signal can even be used as the local replica to realize the matching receiving, for which the CCF is shown as Figure 7(c).
In order to quantitatively compare the performance of above three processing modes, equivalent Gabor bandwidth, correlation loss, and average multipath error envelope are used as evaluation indexes to measure the code tracking accuracy, the performance of acquisition and demodulation, and the multipath resisting performance, respectively.
Figure 8(a) and (b) show the equivalent Gabor bandwidth and the correlation loss of these three processing strategies with respect to the front-end double-sided bandwidth, respectively. Figure 8(c) shows the average multipath error envelopes of these three processing strategies, with front-end double-sided bandwidth of 10 megahertz, and multipath-to-direct ratio (MDR) of –5dB.
One can see from Figure 8 that in different processing strategies, the receiving performance presents an obvious graded characteristic. With a narrow bandwidth, the single-component processing mode has the minimum processing complexity, but the largest correlation loss and the lowest ranging accuracy. However, as an increasing number of components are processed jointly, for wideband receivers, not only is the correlation power loss decreased, but also a higher ranging accuracy as well as a better multipath resisting ability can be obtained. That means the innate multiple processing strategies of the MCC signal can provide different tradeoffs between performance and processing complexity to different PNT application requirements. With MCC signals, receivers can obtain various levels of receiving performance by jointly processing different subsets of signal components. This is one of the major advantages of the MCC signal.
Processing Mode Switching
The inherent multi-strategy processing advantage of MCC signal can be taken not only by different types of receivers, but also in different stages of a wideband receiver. The MCC signal allows the receiver to dynamically switch the processing strategy at different processing stages, according to the current working status to achieve balance between processing complexity and accuracy.
From Figure 7, it can be seen that the main peak of CCF under the single-component processing mode is the widest, which can widen the acquisition bins and provide an unambiguous large pull-in range to the tracking loop. As more components are jointly processed, the energy of the CCF increases significantly, and the main peak of the CCF becomes sharper, which implies higher potential tracking accuracy. However, more side peaks appear on both sides of the CCF main peak.
One possible strategy for a wideband MCC signal receiver is using the single-component processing mode in the initial acquisition and pull-in phases, utilizing the wide CCF main peak to obtain a wider search step and a larger pull-in range. After the tracking loop is stabilized, three- and five-component joint processing can be employed incrementally, gradually gaining higher signal-to-noise ratio and sharpening the CCF peak to obtain higher tracking accuracy.
The switching strategies of the processing mode of MCC signals are not limited to this simple mode. In fact, the multi-component multi-subcarrier structure of the MCC signal provides the possibility for the future receivers to explore the diverse switching strategies.
Selective Availability
Since the multiplexing used in MCC signal construction is sufficiently flexible, different signal components in the MCC signal can be configured with different pseudorandom (PN) codes and different spreading modulation waveforms, and can be modulated with different data messages. Therefore, the service provider can assign different codes and messages to different signal components, controlling the access permissions and providing selective performance to different user levels. The receiver selects the corresponding processing mode according to its own privilege level and thus obtains the available acquisition, tracking, and demodulation performances.
For example, as shown in Figure 9, in the five-component design case provided in this section, s3(t), which is located on the carrier frequency, can be assigned to be the open access signal, of which the PN code generation method and the data message structure are fully open. All receivers can access this component with the single-component processing mode, thus obtaining a relatively low signal-to-noise ratio, and a basic ranging accuracy level.
Components s2(t) and s4(t), which are with relatively low subcarrier frequencies, can be assigned as the secondary authorized signals. Their PN code generating information and data message structures are only provided to the authorized secondary users. These users can access three components, so that multi-component joint processing and dynamical mode switching strategies can be used to obtain the improved performance.
Components s1(t) and s5(t) can be assigned as senior authorized signals, with encrypted PN codes and data message structures, serving authorized senior users. Senior authorized receivers can access all the five components, to obtain the most diversified processing strategies, the highest signal-to-noise ratio, and the highest ranging performance.
In addition, if the data structures of different components are well-designed to carry complementary messages — for authorized users who can access multiple components — the time to first fix (TTFF) can be effectively reduced. In theory, the TTFF of a receiver that jointly processes five components can be shortened by 80% over that of the basic single-component receiver.
The case study in this section demonstrates that the MCC signal has a high degree of flexibility in both the broadcasting strategy and the receiving strategy. There are many more possible broadcasting and receiving modes of MCC than those discussed in this example. In fact, this signal structure offers a wide design space for both the system providers and the receiver developers in future.
Conclusions
As a significant infrastructure, GNSS has a long development cycle. This characteristic means that we can only employ existing techniques to meet the demands over the next few decades. Although it is impossible to envision GNSS products and services further out in time, we can enable future development by implementing excellent signal designs with higher adaptability and flexibility.
The contradiction between the need for performance improvement and the fact that power and spectrum resources are limited will be more serious in the next generation of GNSS signal designs. In order to solve this contradiction, this article first proposes the concept of a multi-carrier constant envelope signal, and studies its feasibility as the next generation satellite navigation signal. A corresponding design method based on the CEMIC technique is given, and an example is presented to demonstrate the RF compatibility, typical receiving strategies, corresponding performances and selection availability of MCC signals. The analyses show that the MCC signal can make full use of the existing spectrum resources, providing both various broadcast strategies and multiple receiving strategies with a variety of performance levels for different categories of users. This technique can serve as a practical new solution to the next generation satellite navigation signals design.
Acknowledgment
This article is based on a presentation given by the first author at the ION GNSS+ 2017 conference on September 27-29, 2017, hosted by the Institute of Navigation in Portland, Oregon, USA. This work is supported by National Natural Science Foundation of China (NSFC), under Grant 61771272.
Additional Resources
[1] Avila-Rodriguez, J.-A., S. Wallner, G. W. Hein, B. Eissfeller, M. Irsigler, and J.-L. Issler, “A vision on new frequencies, signals and concepts for future GNSS systems,” in Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation, Fort Worth, TX, 2007, pp. 517-534.
[2] Emmanuele, A., et alia., “Evaluation of Filtered Multitone (FMT) Technology for Future Satellite Navigation Use,” Proceedings of the 24th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2011), pp. 3743-3755, 2011.
[3] Irsigler, M., G. W. Hein, and A. Schmitz-Peiffer, “Use of C-Band frequencies for satellite navigation: benefits and drawbacks,” GPS Solutions, vol. 8, no. 3, pp. 119-139, 2004.
[4] Lestarquit, L., G. Artaud, and J.-L. Issler, “AltBOC for Dummies or Everything You Always Wanted to Know About AltBOC,” presented at the ION GNSS 2008, Savannah, GA, US, 2008.
[5] Mateu, I., et alia., “A search for spectrum: GNSS signals in S-band, part 2,” Inside GNSS, vol. 2010, no. October, pp. 46-53, 2010.
[6] Pratt, A. R. and J. I. Owen, “BOC modulation waveforms,” in Proceedings of the 16th International Technical Meeting of the Satellite Division of the Institute of Navigation, ION-GPS/GNSS-2003, 2003, pp. 1044-1057.
[7] Thevenon, P. et alia, “Pseudo-Range Measurements Using OFDM Channel Estimation,” (in English), Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2009), pp. 481-493, 2009.
[8] Yao, Z., J. Zhang, and M. Lu (2016), “ACE-BOC: dual-frequency constant envelope multiplexing for satellite navigation,” IEEE Transactions on Aerospace and Electronic Systems, vol. 52, no. 1, pp. 466-485, 2016.
[9] Yao, Z., F. Guo, J. Ma, and M. Lu (2017a), “Orthogonality-based generalized multicarrier constant envelope multiplexing for DSSS signals,” IEEE Transactions on Aerospace and Electronic Systems, vol. 53, no. 4, 2017.
[10] Yao, Z., and L. Mingquan. (2017b) Signal Multiplexing Techniques for GNSS: The principle, progress, and challenges within a uniform framework. IEEE Signal Processing Magazine.
[11] Zhang, X. M., X. Zhang, Z. Yao, and M. Lu (2012), “Implementations of Constant Envelope Multiplexing based on Extended Interplex and Inter-Modulation Construction Method,” (in English), Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation, pp. 893-900, 2012.
[12] Zhang, X., Z. Yao, X. Zhang, and M. Lu (2011), “A Method to Optimize the Spreading Code Chip Waveform in Sense of Gabor Bandwidth,” in Proceedings of the 24th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2011), 2011, pp. 1299-1304.
[13] Zhang, K., “Generalised constant-envelope DualQPSK and AltBOC modulations for modern GNSS signals,” Electronics letters, vol. 49, no. 21, pp. 1335-1337, 2013.