An approach leveraging time-transfer from Earth-GPS.
SRIRAMYA BHAMIDIPATI, TARA MINA, GRACE GAO, STANFORD UNIVERSITY
More than 50 years after the Apollo program, we are entering a “second Space Race,” seeking to not only return humans to the Moon, but to further establish a sustainable human presence. In the coming decade, NASA Artemis missions will land the first woman and person of color on the lunar south pole. More than 40 lunar missions by 10 international space agencies are also lined up in the next decade. Furthermore, this round of space missions will have crucial involvement from commercial space industry companies, including SpaceX and Blue Origin.
The upcoming endeavor of building the first lunar stations that support life away from Earth will serve as a crucial steppingstone for the success of future deep space missions [1]. With significant increases expected in crewed and robotic activities, future lunar missions will require reliable and precise Position, Navigation, and Timing (PNT) services everywhere on the Moon.
Recently, the NASA Goddard Space Flight Center (GSFC) and the European Space Agency (ESA) have conceptualized GPS-like satellite constellations around the Moon, named LunaNet [2]
and Moonlight [3], respectively. Correspondingly, there exist rich preliminary studies on the design of future lunar navigation constellations [4–7]. These NASA and ESA lunar PNT constellations will assist in the overarching effort of establishing a sustainable human presence on the Moon by providing global PNT and communication services to lunar users. In particular, in the next decade, these initiatives seek to satisfy needs expressed by the global exploration community, with a targeted position accuracy of less than 50 m for lunar users [3].
While the lunar positioning accuracy using a lunar navigation satellite system (LNSS) depends on a variety of different factors, a few key ones among them are listed as follows: a) the lunar User Equivalent Ranging Error (UERE), b) the constellation size, c) the Dilution of Precision (DOP), d) the minimum received power, which affects signal acquisition and tracking performance, and e) the overall cost, which depends on the launch costs from Earth, injection costs into stable orbit around the moon, and onboard equipment and its maintenance costs. This article assesses the LNSS design in terms of lunar UERE. Assessment for other factors will be explored in our future works.
There has been an emerging interest in the use of a SmallSat platform for the lunar satellite constellation to allow for cost-effectiveness and rapid deployment [2]. Designing a SmallSat-based LNSS involves unique challenges as compared to legacy Earth-GPS, leading to additional design limitations, including:
Limited size of LNSS satellites. A SmallSat platform limits its payload capacity, including the size, weight and power (SWaP) of the onboard clock. Given that lower SWaP clocks tend to have worse timing stabilities [8], the SWaP limitation of the clock directly affects the ranging accuracy of transmitted navigation signals;
Limited ability to monitor LNSS satellites. Given that a limited number of ground monitoring stations can be established on the Moon and that resources on Earth for monitoring the lunar constellation are limited, it is desirable for LNSS satellites to require less maintenance, including fewer stationkeeping maneuvers and clock correction maintenance; and
Increased orbital perturbations in lunar environment. Because the Moon has a highly non-uniform distribution of mass, its gravitation field is more anisotropic than Earth’s. In addition, Earth’s gravity can significantly impact satellites in high-altitude orbits around the Moon, thereby limiting the set of feasible and stable lunar orbits.
However, only a few prior works [9,10] account for SWaP constraints imposed by SmallSats in a standalone manner (i.e., without having to rely on the ground monitoring infrastructure of Earth or the Moon). Furthermore, these works do not estimate a measure of lunar UERE and its variation based on the lunar orbit type and the grade of onboard clock. Similar to the UERE metric defined for an Earth-GPS satellite, the lunar UERE provides key insights regarding the LNSS design at satellite level, as it characterizes the ranging accuracy of transmitted signals from an LNSS satellite, and thereby affects the position accuracy achieved by a lunar user.
Drawing inspiration from GPS time-transfer techniques for terrestrial applications [11], in this work we harness the legacy Earth-GPS signals to alleviate challenges in designing a SmallSat-based LNSS. In particular, one can perform time-transfer from Earth-GPS to correct a lower-grade clock onboard an LNSS satellite, thereby mitigating the need to install and maintain ground stations on the Moon and/or the need to schedule one-on-one communication with Earth’s ground stations.
While the use of Earth-GPS for near-Earth space applications is well-researched, using Earth-GPS signals for lunar satellites is not straightforward. This is because the Earth-GPS transmit antennas point toward Earth, as shown in Figure 1, thus causing a major part of its main lobe to be occluded by Earth. Thus, Earth-GPS signals are received in lunar orbits from the side lobes and small, unoccluded parts of the main lobe of Earth-GPS satellites, which are located at the far side of Earth, as shown in Figure 1.
Furthermore, the Earth-GPS satellites are only intermittently available due to occultation from both Earth and the Moon. Additionally, because the received carrier-to-noise density (C/N0) depends on the transmit antenna power and free-space path loss, the Earth-GPS signals are largely attenuated at lunar distances of about 385,000 km from Earth.
At the same time, there has been significant progress toward expanding the Earth-GPS service volume to include users in cislunar space. The NASA GSFC has pioneered work in developing the Navigator, a fully space-flight-qualified GNSS receiver with the ability to track very weak Earth-GPS signals [12]. The Navigator is scheduled for testing on the Moon in 2023 during the lunar GNSS receiver experiment [13] and will be the first GNSS positioning fix on the lunar surface. On a similar note, the SpacePNT has developed a high sensitivity spaceborne GNSS receiver named NAVIMOON that will orbit the Moon onboard the ESA’s lunar Pathfinder. It will perform the first GNSS positioning fix in a lunar orbit [14].



Our LNSS Design Using Time-Transfer from Earth-GPS
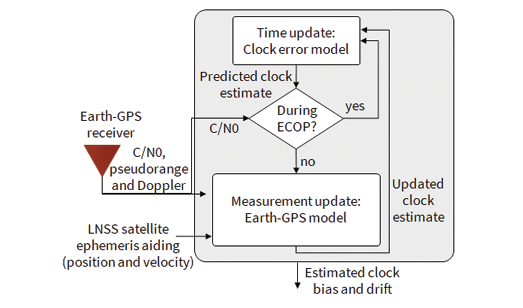
We propose the design of a SmallSat-based LNSS with time-transfer from Earth-GPS [15-17], wherein each LNSS satellite will listen to signals already broadcast by the Earth-GPS and process those signals to estimate timing corrections, as illustrated in Figure 2a. We design a timing filter that corrects the lower-grade clock onboard an LNSS satellite when Earth-GPS signals are available. When Earth-GPS signals are unavailable, we propagate these clock estimates forward in time. We develop an Earth-GPS continual outage period (ECOP) metric to analyze the visibility effects of Earth-GPS on the timing stability of the onboard clock. We also devise a mathematical formulation of the lunar UERE metric, which is proportional to the root-mean-square (RMS) timing error, to analyze the ranging accuracy of an LNSS satellite. We perform an extensive case study analysis to illustrate the trade-off between the different design considerations of the onboard clock and the orbit type for an LNSS design that leverages Earth-GPS time-transfer. Our proposed Earth-GPS-to-LNSS time-transfer technique alleviates requirements with regards to timing stability and, correspondingly, the SWaP of the onboard clock.
At any LNSS satellite, our proposed timing filter, depicted in Figure 2b, maintains a two-dimensional state vector, consisting of the clock bias and drift. For the time update step of our timing filter, we define the process noise covariance in terms of the power spectral density coefficients h0, h−1, h−2 from the clock Allan deviation plot [18], which reflect the short-term and long-term stability of the onboard clock. When performing an Earth-GPS measurement update, we formulate a measurement residual vector by leveraging the position aiding information from available ephemeris for the LNSS satellite. We model the measurement covariance as a time-dependent diagonal matrix [15] based on the receiver tracking errors [19,20], the Earth-GPS UERE [19] and the expected error in available LNSS satellite ephemeris (via onboard orbit determination).
Based on the RMS error in our filter estimate, we formulate a lunar UERE metric that characterizes the accuracy of the LNSS ranging signals for lunar users. On the Moon, any atmospheric delays are minimal. Moreover, we consider multipath effects experienced by users on the lunar surface to be negligible due to the lack of building infrastructure and foliage. As a result, the lunar UERE can be computed in terms of the four most significant error components as follows:

where the errors due to the differential group delay σgd,LNSS and the receiver noise σrec,LNSS will depend on the finalized LNSS signal structure and lunar user receiver. Note that, because the timing filter uses position aiding from the LNSS satellite, the lunar ephemeris error component σeph,LNSS directly impacts the pseudorange residual measurement received at the LNSS satellite, which will thus also affect the LNSS onboard clock error σclk,LNSS.
In this work, we investigate how the LNSS clock error component σclk,LNSS differs for various grades of onboard clocks and lunar orbits, while also analyzing the impact on lunar UERE. We additionally analyze lunar UERE for a potentially reduced measurement update rate when Earth-GPS signals are available, with a sampling period of Tmeas=mTpred seconds, where m is a positive integer and Tpred is the rate at which time update step is executed. Indeed, a larger choice of m corresponds to less frequent measurement updates, which allows the Earth-GPS receiver to be switched off for a longer time duration to save power.
Overview of Case Studies on Clocks and Orbits
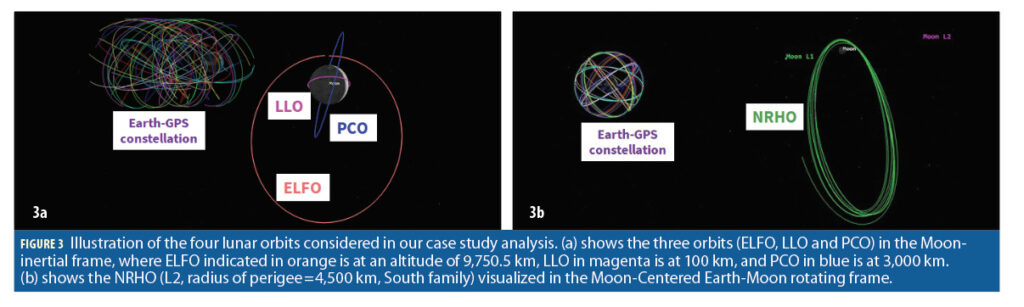
We design our case study analysis by simulating an LNSS satellite in various lunar orbit types. In particular, several types of lunar orbits that have previously been investigated include low lunar orbit (LLO), prograde circular orbit (PCO), near-rectilinear halo orbit (NRHO), and elliptical lunar frozen orbit (ELFO). ELFOs refer to a specific category of frozen orbits providing a greater coverage of the lunar poles, wherein the term frozen indicates that these orbits maintain nearly constant orbital parameters for extensive periods of time, without requiring stationkeeping [21,22]. Although PCOs are not frozen, they maintain multi-year stability with orbital parameters exhibiting predictable, repeatable behavior [22]. Due to their low orbiting altitude, LLOs have shorter orbital periods around the Moon, and there exist a few inclinations in which LLOs are also considered to be frozen or quasi-frozen [21]. While NRHOs are less stable than the above orbits, thereby requiring more frequent stationkeeping maneuvers, these orbits are highly elliptical with nearly constant visibility of Earth and the lunar poles [7].
For each orbit type, we design a high-fidelity simulation of an LNSS satellite using the Systems Tool Kit (STK) software by Analytical Graphics, Inc. (AGI) [23]. For each modeled orbit type, we design case studies in MATLAB by simulating various grades of onboard clocks. For each case study, we consider the start time epoch to be 9 Nov 2025 00:00:00.000 UTC and the experiment time duration to be 2 months. We create realistic simulations of an LNSS satellite in different lunar orbits by leveraging the High Precision Orbit Propagator (HPOP) in the STK software [23].
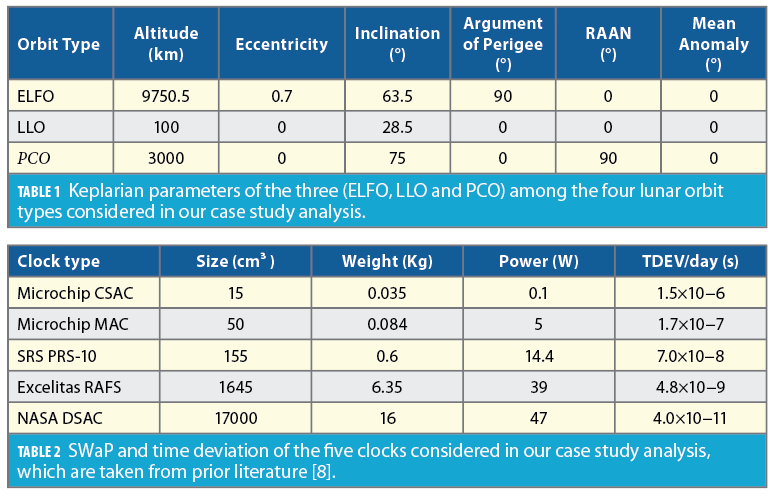
We model the three orbit types, namely ELFO, LLO and PCO, in the STK software using classical orbit mechanics. Specifically, we refer to prior literature [22, 24, 25] for defining the corresponding six Keplarian parameters at the start time epoch, which includes semi-major axis, eccentricity, inclination, argument of perigee, Right Ascension of the Ascending Node (RAAN), and mean anomaly.
Table 1 lists these Keplarian parameters while Figure 3a shows the orbit illustration in the Moon-inertial frame. In contrast, we refer to prior literature [26] for modeling the fourth lunar orbit, namely L2 South NRHO, that involves specifying the initial position and velocity in the Moon-centered Earth-Moon rotating frame. In the Earth-Moon rotating frame, which is particularly useful when discussing halo orbits in the Earth-Moon system, the x-axis is along the instantaneous Earth-Moon position vector, the z-axis is along the instantaneous angular momentum vector of the Moon’s orbit around Earth, and the y-axis completes the orthogonal system. The illustration of our NRHO is shown in Figure 3b.
Based on prior literature [8], our choice of clock types for this work includes Microchip Chip Scale Atomic Clock (CSAC), Microchip Micro Atomic Clock (MAC), Stanford Research Systems (SRS) PRS-10, Excelitas Rubidium Atomic Frequency Standard (RAFS) and NASA’s Deep Space Atomic Clock (DSAC) [27]. The specifications of these clock types are listed in Table 2 and have been arranged in the increasing order of their SWaP for convenience.
For each clock type, we simulate the true clock error model in MATLAB to have a constant drift in the clock bias and thereafter propagate the clock states forward in time using a first-order state transition matrix. We assign the true clock drift (constant value) based on the known specifications of Time Deviation (TDEV) observed at the end of a day, which are reported in Table 2. Note that, for any clock type, TDEV refers to the expected error in reported time after a certain holdover time that essentially depends on their respective values of Allan deviation and frequency drift.
For time-transfer from Earth-GPS, we simulate an Earth-GPS constellation of 31 satellites with eight satellites from Block IIR, seven from IIRM, 12 from IIF and four from Block III. We model the transmit antenna of Earth-GPS satellites by using the transmit power and antenna gain patterns of the L1 C/A signals, which are made available from the NASA GPS (Antenna Characterization Experiment) ACE study [28]. We also simulate a spaceborne Earth-GPS receiver at the LNSS satellite with a steering antenna pointed toward the Earth so as to maximize the visibility of Earth-GPS signals at the LNSS satellite. Based on prior literature [19, 24], we consider a high-gain antenna with 14 dBi at 0° off-boresight angle, and a 3dB beamwidth of 12.2°. We consider an Earth-GPS satellite to be visible when the received C/N0 value is greater than 15dB−Hz for a continuous time duration of at least 40 s.
Our Case Study Analysis: Results and Discussion
We analyze the trade-off across different case studies related to the onboard clock and the orbit type in terms of lunar UERE. For this, we consider the same group delay and receiver noise error magnitudes as with the Earth-GPS system, i.e. σgd,LNSS=0.15 m and σrec,LNSS=0.1m. Given that the future LNSS will have greater limitations on ground monitoring infrastructure as compared to Earth-GPS, we set the error component due to the broadcast ephemeris in the lunar UERE as σeph,LNSS=3 m (an order of magnitude higher than Earth-GPS). We design our timing filter with the time update executed every Tpred=60 s.
Validation Metrics
We define the following four validation metrics:
1. Satellite visibility, which indicates the percentage time of the entire experiment for which the number of visible Earth-GPS satellites are greater than pre-specified thresholds of a) at least 1, minimum number required to estimate the clock bias and drift; and b) at least 4, required to estimate full state vector that includes position, clock bias, velocity and clock drift;
2. Maximum ECOP to identify the region of maximum continuous time when no Earth-GPS satellites are visible;
3. RMS errors in clock estimates across the simulation time duration to analyze the performance of our time-transfer from Earth-GPS for a reduced measurement update rate with a sampling period of Tmeas=mTpred, where m=5; and
4. Lunar UERE metric that characterizes the ranging accuracy of LNSS navigation signals and depends on the RMS error of our timing filter. This is analyzed for different reduced measurement update rates with m= 1, 5, 30, 60. Note that, m=1 depicts the baseline comparison case (not reduced rate) where the measurement update step is executed whenever Earth-GPS satellites are visible.
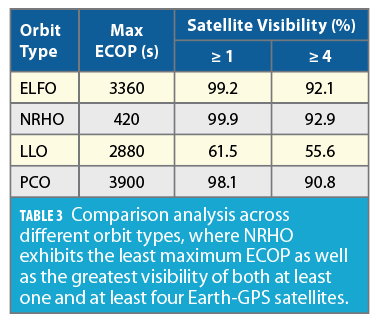
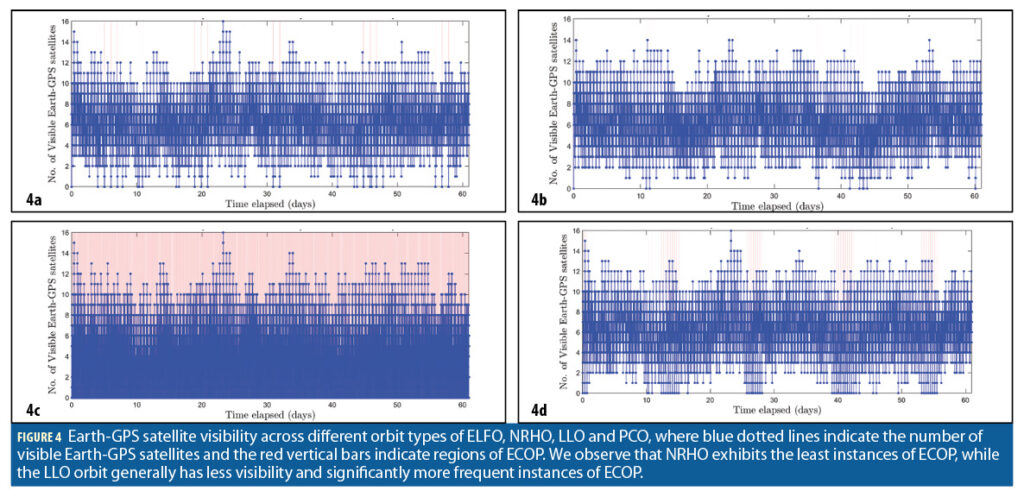
Across Orbit Types: Variation in Satellite Visibility and Maximum ECOP
For the four orbit types considered, we showcase the number of visible Earth-GPS satellites by blue in Figure 4 while the highlighted red vertical bars indicate the regions of ECOP. Based on Table 3, we observe that NRHO achieves the greatest at least one satellite visibility, which is 99.9% of the total time, and also the greatest at least four satellite visibility, which is 92.9% of the total time. Furthermore, NRHO also exhibits the least maximum ECOP of only 420s, while the other orbit types experience ECOP of at least 2,880s. Indeed, an LNSS satellite in NRHO operates at high altitudes ranging between 4,500km to 700,000km above the Moon’s surface, and thus experiences fewer occultations from Earth and the Moon. We observe that LLO, which has a low altitude of 100km, exhibits the smallest time spacing between consecutive ECOPs.
Across Clock Types: Variation in RMS Timing Errors
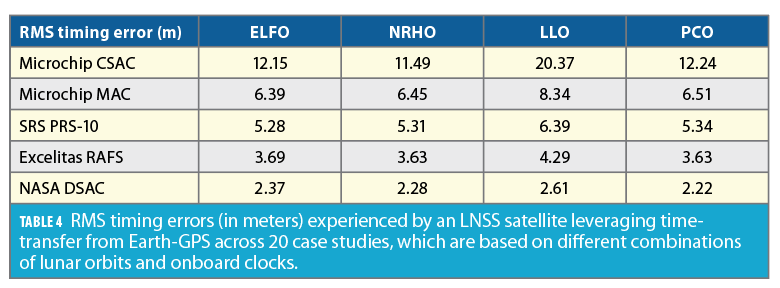
Table 4 compares the RMS timing error (estimation error in clock bias) across different case studies, which provides insights regarding the clock error component σclk,LNSS of the lunar UERE metric. For a reduced measurement update rate of Tmeas=mTpred with m=5, we observe that the three orbit types, namely ELFO, NRHO and PCO, demonstrate a comparable RMS timing error of <12.24m (equivalent to 0.0408 microseconds), while the case study based on LLO shows a higher RMS timing error of 20.37m (equivalent to 0.0679 microseconds).
As SWaP and timing stability of the onboard clock increases, we also observe that the variation in RMS timing error across orbit types becomes less significant, wherein the RMS timing error of DSAC is <2.61 m (equivalent to 0.0087 microseconds). Note there is only a small degree of correlation between the orbital viewing geometry for the least stable clock, say CSAC. This is because the mean distance between Earth-GPS and the LNSS satellite is already quite large (approximately 385,000 km), thus altitude variations in the lunar orbit, which are in the order of only thousands, are not enough to induce a significant difference in timing errors. This is indeed quite an interesting observation, as it ensures uniformity in the accuracy of onboard clock estimates, even if a hybrid constellation involving varied lunar orbit types are considered in the future LNSS.
Across Case Studies and Earth-GPS Measurement Update Rates: Sensitivity Analysis of Lunar UERE
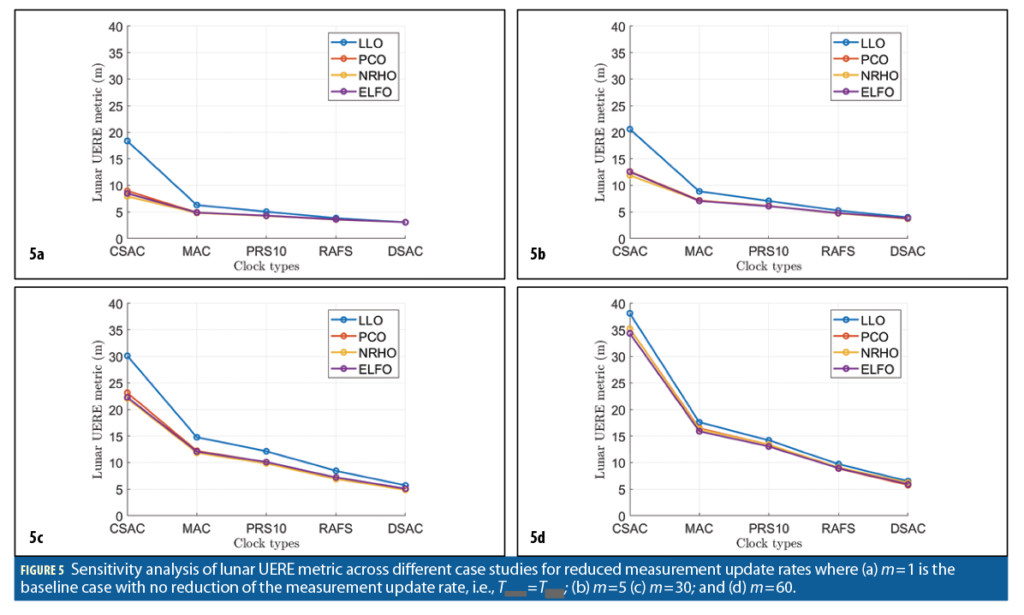
Figure 5a demonstrates the variation in the lunar UERE metric, as estimated using Equation 1, across case studies conducted while considering no reduction in the measurement update rate, i.e., m=1. We validate that our proposed time-transfer achieves a low lunar UERE of <10m for most case studies except the one involving the LLO and the Microchip CSAC, which exhibits a value of 18.4m. These observations imply that, if the desired lunar UERE to be maintained by an LNSS satellite is, for instance, <10m at all times, we can easily opt for an onboard clock that falls in the lower end of the SWaP spectrum, such as Microchip CSAC or Microchip MAC, instead of a high-SWaP clock, such as Excelitas RAFS or NASA’s DSAC. We also demonstrate that we can wisely choose the orbit type that is easy to maintain, such as LLO, PCO or ELFO, over the more complex NRHO that requires frequent stationkeeping to maintain stability.
Figures 5b-5d show the variation in lunar UERE metric for three cases of reduced update rates, where Tmeas=mTpred with m=5, m=30 and m=60 respectively. Note that Table 4 represents the LNSS clock error component σclk,LNSS of lunar UERE (in meters) for m=5 case.
As the Earth-GPS measurement update rate increases for low-SWaP clocks with sampling periods from Tmeas=60 min (m=60) to Tmeas=1 min (m=1), we observe an increased sensitivity of the lunar UERE metric across lunar orbits, i.e., difference in value between LLO and others increases. We also demonstrate that the estimated lunar UERE is <30m for a reduced Earth-GPS measurement update rate with a sampling period of up to Tmeas=30 min, which is comparable in order of magnitude to the baseline case with m=1 (Figure 5a) as well as the legacy Earth-GPS. Thus, even at a reduced measurement update rate, we validate that our LNSS design that uses time-transfer from Earth-GPS lowers the SWaP requirements of the onboard clock.
Conclusion
We designed an Earth-GNSS-to-LNSS time-transfer architecture that alleviated the SWaP requirements of the onboard clocks by leveraging the Earth-GPS signals to provide timing corrections. We additionally investigated which design considerations, including grade of onboard clock and lunar orbit type, for the SmallSat-based LNSS best leverages the intermittently available Earth-GPS signals to reduce the lunar UERE. Indeed, lunar UERE is one of the key components for determining the navigation performance provided by the LNSS for future lunar missions. By analyzing multiple case studies, we demonstrated that lower SWaP onboard clocks and easier-to-maintain lunar orbits can achieve a desirable lunar UERE, which can satisfy the targeted positioning accuracy of less than 50 m with sufficiently low DOP from the LNSS constellation.
We will extend this analysis to design the complete SmallSat-based LNSS constellation, which leverages Earth-GPS time-transfer, to achieve desired PNT performance for lunar missions.
Acknowledgments
We would like to thank the Analytical Graphics, Inc. (AGI) Educational Alliance Program (EAP) for providing us with the System Tool Kit (STK) software license to perform this research work. We would also like to thank Keidai Ilyama for the insightful discussions related to this work.
References
(1) Laurini, K. C. and Gerstenmaier, W. H., “The global exploration roadmap and its significance for NASA,” Space Policy, vol. 30, no. 3, pp. 149–155, 2014.
(2) Israel, D. J., Mauldin, K. D., Roberts, C. J., Mitchell, J. W., Pulkkinen, A. A., La Vida, D. C., Johnson, M. A., Christe, S. D., and Gramling, C. J., “LunaNet: A flexible and extensible lunar exploration communications and navigation infrastructure,” in 2020 IEEE Aerospace Conference. IEEE, 2020, pp. 1–14.
(3) Cozzens, T., “Galileo will help lunar pathfinder navigate around Moon,” GPS World, 2021. [Online]. Available: https://www.gpsworld.com/galileo-will-help-lunar-pathfinder-navigate-around-moon/?utm_source=Navigate!+Weekly+GNSS+News&utm_medium=Newsletter&utm_campaign=NCMCD210331002&oly_enc_id=6244C4859912F3Z
(4) Murata, M., Kawano, I., and Kogure, S., “Lunar navigation satellite system and positioning accuracy evaluation,” in Proceedings of the 2022 International Technical Meeting of The Institute of Navigation. Institute of Navigation, feb 2022, pp. 582–586. [Online]. Available: https://doi.org/10.33012%2F2022.18220.
(5) Pereira, F. and Selva, D., “Exploring the design space of lunar GNSS in frozen orbit conditions,” in 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS). IEEE, apr 2020, pp. 444–451. [Online]. Available: https://doi.org/10.1109%2Fplans46316.2020.9110202
(6) ——, “Analysis of navigation performance with lunar GNSS evolution,” in Proceedings of the 2022 International Technical Meeting of The Institute of Navigation. Institute of Navigation, feb 2022, pp. 514–529. [Online]. Available: https://doi.org/10.33012%2F2022.18210.
(7) Schonfeldt, M., Grenier, A., Delépaut, A., Giordano, P., Swinden, R., Ventura-Traveset, J., Blonski, D., and Hahn, J., “A system study about a lunar navigation satellite transmitter system,” in 2020 European Navigation Conference (ENC). IEEE, 2020, pp. 1–10. [Online]. Available: https://doi.org/10.23919%2Fenc48637.2020.9317521.
(8) Schmittberger, B. L. and Scherer, D. R., “A review of contemporary atomic frequency standards,” arXiv preprint arXiv:2004.09987, 2020. [Online]. Available: https://arxiv.org/pdf/2004.09987.pdf.
(9) Batista, A., Gomez, E., Qiao, H., and Schubert, K., “Constellation design of a lunar global positioning system using cubesats and chip-scale atomic clocks,” in WorldComp, 2012.
(10) Iiyama, K., Kawabata, Y., and Funase, R., “Autonomous and decentralized orbit determination and clock offset estimation of lunar navigation satellites using GPS signals and inter-satellite ranging,” in Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021). Institute of Navigation, oct 2021. [Online]. Available: https://doi.org/10.33012%2F2021.18019.
(11) Wouters, M. J. and Marais, E. L., “GPS-based time transfer using low-cost receivers,” MAPAN, vol. 34, no. 4, pp. 521–528, may 2019. [Online]. Available: https://doi.org/10.1007%2Fs12647-019-00322-y.
(12) Winternitz, L. M. B., Bamford, W. A., and Heckler, G. W., “A GPS receiver for high-altitude satellite navigation,” IEEE Journal of Selected Topics in Signal Processing, vol. 3, no. 4, pp. 541–556, aug 2009. [Online]. Available: https://doi.org/10.1109%2Fjstsp.2009.2023352.
(13) Parker, J. J., Dovis, F., Anderson, B., Ansalone, L., Ashman, B., Bauer, F. H., D’Amore, G., Facchinetti, C., Fantinato, S., Impresario, G., McKim, S. A., Miotti, E., Miller, J. J., Musmeci, M., Pozzobon, O., Schlenker, L., Tuozzi, A., and Valencia, L., “The lunar GNSS receiver experiment (LuGRE),” in Proceedings of the 2022 International Technical Meeting of The Institute of Navigation. Institute of Navigation, feb 2022, pp. 420–437. [Online]. Available: https://doi.org/10.33012%2F2022.18199.
(14) Cozzens, T., “Galileo will help Lunar Pathfinder navigate around Moon,” GPS World, Mar. 2021. [Online]. Available: https://www.gpsworld.com/galileo-will-help-lunar-pathfinder-navigate-around-moon/.
(15) Bhamidipati, S., Mina, T., and Gao, G., “Design considerations of a lunar navigation satellite system with time-transfer from Earth-GPS,” in Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021). Institute of Navigation, Oct. 2021, pp. 950–965.
(16) ——, “A case study analysis for designing a lunar navigation satellite system with time-transfer from earth-GPS,” in Proceedings of the 2022 International Technical Meeting of The Institute of Navigation. Institute of Navigation, Feb. 2022. [Online]. Available: https://doi.org/10.33012%2F2022.18202.
(17) —— (2022). Time Transfer From GPS for Designing a SmallSat-Based Lunar Navigation Satellite System. NAVIGATION: Journal of the Institute of Navigation, 69(3).
(18) Krawinkel, T. and Schön, S., “Benefits of receiver clock modeling in code-based GNSS navigation,” GPS Solutions, vol. 20, no. 4, pp. 687–701, 2016.
(19) Kaplan, E. D. and Hegarty, C., Understanding GPS/GNSS: Principles and applications. Artech House, 2017. [Online]. Available: https://dl.acm.org/doi/10.5555/3158927.
(20) Capuano, V., Basile, F., Botteron, C., and Farine, P.-A., “GNSS-based orbital filter for Earth Moon Transfer Orbits,” The Journal of Navigation, vol. 69, no. 4, pp. 745–764, 2016.
(21) Folta, D. and Quinn, D., “Lunar frozen orbits,” in AIAA/AAS Astrodynamics Specialist Conference and Exhibit, 2006, p.6749.
(22) Whitley, R. and Martinez, R., “Options for staging orbits in cislunar space,” in 2016 IEEE Aerospace Conference. IEEE, 2016, pp. 1–9.
(23) “Systems Tool Kit (STK),” AGI, 2021. [Online]. Available: https://www.agi.com/products/stk
(24) Ely, T. A. and Lieb, E., “Constellations of elliptical inclined lunar orbits providing polar and global coverage,” Journal of the Astronautical Sciences, vol. 54, no. 1, pp. 53–67, 2006.
(25) Delépaut, A., Schönfeldt, M., Giordano, P., Blonski, D., Sarnadas, R., Ries, L., and Ventura-Traveset, J., “A system study for cislunar radio navigation leveraging the use of realistic galileo and gps signals,” in Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), 2019, pp. 1199–1219.
(26) Williams, J., Lee, D. E., Whitley, R. J., Bokelmann, K. A., Davis, D. C., and Berry, C. F., “Targeting cislunar near rectilinear halo orbits for human space exploration,” 2017.
(27) Ely, T. A., Burt, E. A., Prestage, J. D., Seubert, J. M., and Tjoelker, R. L., “Using the deep space atomic clock for navigation and science,” IEEE transactions on ultrasonics, ferroelectrics, and frequency control, vol. 65, no. 6, pp. 950–961, 2018.
(28) Donaldson, J. E., Parker, J. J., Moreau, M. C., Highsmith, D. E., and Martzen, P. D., “Characterization of on-orbit GPS transmit antenna patterns for space users,” NAVIGATION, Journal of the Institute of Navigation, vol. 67, no. 2, pp. 411–438, 2020.
Authors
Sriramya Bhamidipati is a postdoctoral scholar in the Aeronautics and Astronautics Department at Stanford University. She received her Ph.D. in Aerospace Engineering at the University of Illinois, Urbana-Champaign in 2021, where she also received her M.S in 2017. She obtained her B.Tech. with Honors in Aerospace from the Indian Institute of Technology, Bombay in 2015. Her research interests include GPS, unmanned aerial vehicles, artificial intelligence, computer vision, power and space systems.
Tara Mina is a Ph.D. candidate in the Electrical Engineering Department at Stanford University. She received her B.S. degree in Electrical Engineering from Iowa State University in 2017 and completed her M.S. degree in Electrical and Computer Engineering from the University of Illinois at Urbana-Champaign in 2019. Her research interests include secure and reliable positioning, navigation and timing as well as GPS signal design.
Grace Gao is an assistant professor in the Department of Aeronautics and Astronautics at Stanford University. Before joining Stanford University, she was an assistant professor at University of Illinois at Urbana-Champaign. She obtained her Ph.D. at Stanford University. Her research is on robust and secure positioning, navigation and timing with applications to manned and unmanned aerial vehicles, robotics, and power systems.