For the complete story, including figures, graphs, and images, please download the PDF of the article, above.
Knowledge of carrier-to-noise ratio (CNR) can be of great value in the context of GNSS.
For the complete story, including figures, graphs, and images, please download the PDF of the article, above.
Knowledge of carrier-to-noise ratio (CNR) can be of great value in the context of GNSS.
In addition to determining the relative signal to noise strength, CNR information can assist various stages of signal tracking in a GNSS receiver. For example, CNR measurements may serve as status indicators of the code and carrier tracking loops by detecting the presence of loss-of-lock events. A receiver may also incorporate CNR estimates in its tracking stages for increasing the accuracy of the estimated synchronization parameters, enhancing multipath mitigation techniques, or as a triggering mechanism for switching among tracking algorithms to optimize performance in various CNR ranges.
The multitude of possible applications for CNR measurements is far from being exhausted. In order to efficiently serve existing and future CNR-based applications, receiver designs that maximize estimation accuracy become paramount. Whilst the technical literature contains plenty of paradigms, many GNSS-specific estimation methods are limited by sensitivity to noise power or perform poorly performance in low CNR conditions.
Situations in which higher estimation accuracy is desired may lead to techniques that require higher computational complexity. Acknowledging this trade-off, we propose a new CNR estimation technique called level-crossing-rate estimation (LCRE), which exhibits optimal performance under very noisy conditions.
Statistical Characterization of Signals
One of the main functions that a GNSS receiver performs is the cross-correlation of the received signal with a stored reference in order to match up the same pseudorandom noise (PRN) code. This process also incorporates a certain estimate of Doppler frequency and code delay.
. . .
Derivation of the Level-Crossing-Rate Estimator
Traditionally, the level crossing rate (LCR) information has been widely used in the field of wireless communications for optimizing various receiver parameters, such as modulation format, frame length, and automatic gain control (AGC). LCR information is also used for computing the average error performance of beamforming receivers and estimating the maximum Doppler frequencies or the speed of a mobile receiver.
In the context of satellite-based positioning, usage of LCR information has been rather sparse and only in connection with fading channel characterization and Doppler spread estimation. Despite this, the concept of associating LCR with accurate CNR estimation is, according to our knowledge, completely new.
. . .
Look-Up Table Reduces Computing Time
In order to reduce the complexity of the algorithm, we compute the CDFs for different level crossings and store the values in a look-up table. After the median of the CCF is computed, we compare it with those in the look-up table and choose the CDF output with the best level crossing match.
. . .
CNR Estimators
Typical CNR estimators for GNSS signals are based on the first- or higher order moments of the CCF output. Among the least computationally demanding, we find the first- and second-order moment (1stOM and 2ndOM, respectively) based estimators with which to estimate CNR . . .
. . .
Comparing Estimators’ Performance
In this section, we compare the simulation results based on performance of the four CNR estimators: 1stOM, 2ndOM, the proposed LCRE, and NWPR. In order to create a fair comparison, we use the same number of OPPs in the moment-based estimators as in our LCRE method, described by KOPP = Ktot – 2NsNB – 1.
The simulations were carried out assuming an infinite bandwidth, a rectangular pulse shaping filter, and an oversampling factor of Ns = 4, where each BOC interval contained four samples. The BOC order was NB = 12, and we set the time-bin equal to 1/(NsNB) millisecond, which is the interval between samples of the correlation function. The smaller the interval is, the more bins along the correlation function we have. Moreover, the output of the correlation function is coherently averaged using Nc = 10 milliseconds, followed by two blocks of non-coherent integration (Nnc = 2).
. . .
Summary and Conclusions
We introduce and derive a new method for estimating CNR, called Level Crossing Rate-based-Estimator (LCRE), by exploiting statistical characteristics of correlation samples. We compare the LCRE method with first- and second-based moments, as well as with the well-known Narrowband-Wideband Power Ratio method.
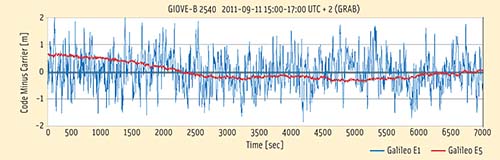
The performance comparison covers both cases of Additive White Gaussian Noise (AWGN) and fading multipath channels. The former is used for investigating the maximum achievable performance, while the latter is chosen for the representation of more realistic scenarios.
Results show the proposed LCRE method performs considerably better than the other three methods under very low CNR conditions, ranging from 5 to 20 dBHz or higher, depending on the scenario. However, the improved performance of LCRE is counterbalanced by its higher computational complexity, mitigated by the implementation of a look-up table.
In cases where low computational complexity is required, the NWPR method provides the best solution. Although the algorithm designer must decide how much computational complexity to trade for improved accuracy, the use of look-up tables reduces the LCRE execution speed.
For the complete story, including figures, graphs, and images, please download the PDF of the article, above.
Acknowledgements
This work was carried out as part of the “Future GNSS Applications and Techniques (FUGAT)” project, funded by the Finnish Funding Agency for Technology and Innovation (Tekes). The work has also been supported by the Tampere Doctoral Program in Information Science and Engineering and by the Academy of Finland.
Additional Resources
[1] Falletti, E.. and Pini, M. and Lo Presti, L. “Are C/N0 algorithms equivalent in all situations?” Inside GNSS, vol. 5, No. 1, January/February, 2010
[2] Islam, A.K.M.N., and E. S. Lohan, and M. Renfors, “Moment-based CNR estimators for BOC/BPSK modulated signal for Galileo/BPSK,” WPNC, Hannover, Germany, March 2008
[3] Lohan, E. S., “Statistical analysis of BPSK-like techniques for the acquisition of Galileo Signals,” in Proceedings of 23rd AIAA International Communications Satellite Systems Conference (IC-SSC), September 2005
[4] Lohan, E. S., “Analysis of Filter-Bank-Based Methods for Fast Serial Acquisition of BOC-Modulated Signals,” EURASIP Journal on Wireless Communications and Networking, Volume 2007, Article ID 25178, 12 pages, doi:10.1155/2007/25178.
[5] Proakis, J., “Digital Communications”, McGraw-Hill, New York, USA, 1995.
[6] Sayre, M. “A Block Processing Carrier to Noise Ration Estimator for the Global Positioning System”, in proceedings of ION NTM, 2004, pp. 862-868.
[7] Skournetou, D., and E. S. Lohan, “Indoor location awareness based on the non-coherent correlation function for gnss signals,” In Proc. of Finnish Signal Processing Symposium (FINSIG’07), Oulu, Finland, August 2007. Available online here
[8] Tsui, J. B.-Y., Fundamentals of Global Positioning System Receivers: a Software Approach, Wiley Interscience, 2005
[9] Van Dierendonck, A.J., "GPS Receivers", Global Positioning System: Theory and Applications. Vol. 1. Eds. B. W. Parkinson and J. J. Spilker, Jr. Washington, DC: American Institute of Aeronautics and Astronautics, pp. 329-407, 1996