Due to the proliferation of personal privacy devices and other jamming sources, it is imperative for safety-critical GNSS users such as airports and marine ports to be situationally aware of local GNSS interference. This article proposes and validates an enhanced method for geolocating GNSS interference sources so that jammers and spoofers can be found and disabled.
Wideband jammers or interference, intentional or not, are most effective at jamming nearby GNSS users as it is frequency agnostic and causes sustained loss of GNSS signal by nearby GNSS users (see Borio et alia, Additional Resources, posted in the online version of this article). Examples of intentional wideband jammers uses modulation schemes such as FM chirp (sometimes also known as swept Continuous Wave) and Additive White Gaussian Noise (AWGN). In comparison, narrowband jammers such as Continuous Wave (CW) are relatively frequency selective and can cause intermittent GNSS operation. Hence, it is imperative to have the ability to identify the presence of a wideband GNSS jammer and geolocate it as they pose a greater danger to GNSS users.
AOA of a Radiofrequency (RF) emitting signal source. Typical passive GNSS interference sensing uses a network of phased arrays to infer two or more Angles of Arrival (AOA). Conventional AOA estimation using phased arrays assumes narrowband signals that satisfy the time bandwidth product:
where ▵T is defined as the maximum distance (in meters) between station pairs and B is defined as the signal bandwidth is Hertz. To accommodate wideband signals, most AOA algorithms (see multiple papers, Additional Resources) partition the signal into multiple narrowband channels for AOA processing. Thus, such methods are attempting to geolocate wideband sources despite the source being wideband. Examples of algorithms that are able to deduce the AOA from phased arrays are MUSIC (Schmidt) and MVDR (Rieken and Fuhrmann).
The AOA measurements from two or more stations can then be used to triangulate the location of the interference source. By deploying multiple stations of phased arrays that are geographically dispersed, AOA estimates retrieved from each station can be used to accurately geolocate a source using techniques such as least-squares that are based on the intersection of AOA lines of position (Dempster)
To exploit fully the wideband characteristics of the source signal, a cross-correlation method needs to be employed. The cross correlation of received signals between two distant stations will produce a distinct peak at a cross-correlation delay with the Time Difference of Arrival (TDOA) of the corresponding source. Hence, TDOA is another sensor station’s observation that relates to the geographical location of the wideband source signal. If there are three or more stations, the combination of two or more detected TDOA measurements can be used to geo-localize the jammer position.
Recently, new methods consider a modified Maximum Likelihood (ML) approach for AOA geo-localization dubbed direct positioning (see both Cheong and Dempster, and Tzafri and Weiss). Indeed, cross-correlation and AOA characteristics can also be simultaneously exploited for geolocation in direct positioning. However, this occurs at the expense of orders of magnitude greater in computational cost and is beyond our scope.
Until recently, source geo-localization algorithms have only considered either AOA measurements or TDOA measurements as independent systems of equations for geo-localization. By and large, conventional algorithms have not appropriately considered the fusion of heteroskedastic (i.e. unequal variances) AOA and TDOA measurements and have not fairly characterised their advantages against pre-existing methods.
Modern techniques have attempted to integrate AOA with TDOA using computationally expensive constrained optimization techniques (Bishop et alia). Another method attempts to integrate AOA with TDOA by assuming at least one Time of Arrival (TOA) is available (Li and Weihua). While this may be afforded by CDMA cellular networks that are active systems, passive sensing systems like those considered here are unable to obtain TOA. Some papers considered unweighted algorithms, not considering that AOA and TDOA measurement standard deviations vary from station to station, which is highly unrealistic (see again Li and Weihua). The most recent progress has been made by Yin et alia where AOA and TDOA are combined for geo-localization in closed form but that method is unable to cope with incomplete information; hence one missing AOA measurement from station i, for example, will result in the complete loss of all TDOA measurements involving station i. This lack of robustness ultimately affects the geo-localization accuracy.
AOA Geolocalization
We consider a vector of AOA measurements from L stations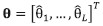 
modelled as a Gaussian distribution
Let us define the source’s TDOA of station i from station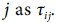 
. Then if we construct the observed TDOA from all stations with reference to station 
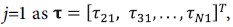the TDOA observation model used is a multivariate Gaussian
distribution. [6].
The mean and the covariance component of the multivariate Gaussian distribution can be further defined as:
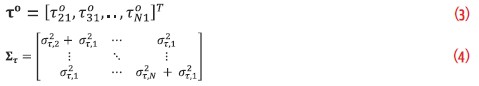
Note that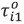 
is the true TDOA of the i-th station from station 1, and 
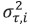is the variance related to the signal arriving at the i-th station.
Given that we are considering a wideband GNSS jammer, we can use cross-correlation signal processing techniques to measure the TDOA arriving between several stations. The TDOA measurement is related to the source coordinates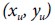 
by
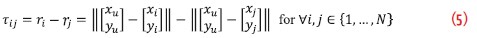
Note that ||.|| is the Euclidean distance of the vector. From its partial derivatives, we can construct the Jacobian matrix for the TDOA measurement vector as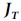 
as described in the paper by Kaune et alia. A Gauss Newton algorithm can be derived using its gradient 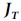for a TDOA-only source geo-localisation algorithm. The implementation of this iterative process can be summarised in Pseudocode 2.
Pseudocode 2 considers TDOAs from a star network topology. If a fully connected network is considered, the algorithm can still cater for all the TDOAs, but its effect on accuracy is negligible. However, in the case where there are certain missing
TDOA measurements, this algorithm can still easily adapt to that. Based on the reasoning for the case of AOA-only geolocalisation, the accompanying error covariance of the position solution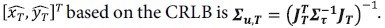 
Proposed AOA/TDOA Integrated Geolocalization
Proposed AOA/TDOA Integrated Geolocalization
This section presents the core contribution of this paper, that is to be able to geolocate by fusing both AOA and TDOA measurements. Given the AOA-only and TDOA-only geolocalization estimates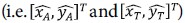 
which can be computed from Pseudocode 1 and Pseudocode 2 and their respective errors covariances 
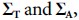their solutions can be found by using the Weighted Least Squares (WLS) as follows,
Where the integrated error covariance matrix and the transformation matrices are respectively,
The appropriately weighted AOA/TDOA loose integration requires perfect knowledge of the AOA-based and TDOAbased position error covariance matrices. The calculation of AOA-only and TDOA-only covariance matrices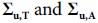 
in turn requires sufficiently accurate coordinates of the source and station. While the station coordinates are known, the source coordinates are generally unknown. In practice, this solution is implemented as an iterative process because the best guess of the source coordinates is at the end of each iteration. Thus, in such an iterative procedure, a guesstimate position from either the AOA or TDOA estimation process can be used in the first iteration to initialize both the TDOA and AOA position covariance matrices. After the AOA/TDOA integration has been performed, subsequent iteration uses the updated position estimates to re-calculate 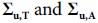. This is repeated until convergence. Indeed, we have experimentally verified that in some, but not all cases when 
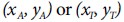is sufficiently accurate, the number of iterations for AOA/TDOA integration K can be as small as one. The maximum number of iterations is considered sufficient when the Euclidean difference between the coordinate estimates 
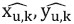of iteration K and K-1 is within a desired tolerance. This convergence principle applies also to Pseudocode 1 and 2. This iterative process is detailed in Pseudocode 3.
While this proposed architecture of integration can be thought of as “loose”, it has the advantage of accommodating existing TDOA-only and/or AOA-only geo-localization implementations that are already in place. It also has very low computational cost and low complexity as it does not require complicated forms of numerical optimization techniques, nor does it require evaluation of non-linear functions, as tighter integration methods do. To obtain the CRLB for the integrated solution, we first need to derive the Fisher Information Matrix (FIM) as
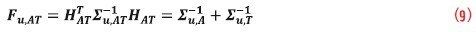
The CRLB for the joint AOA/TDOA geolocation is defined as the inverse of the FIM:
Numerical Results
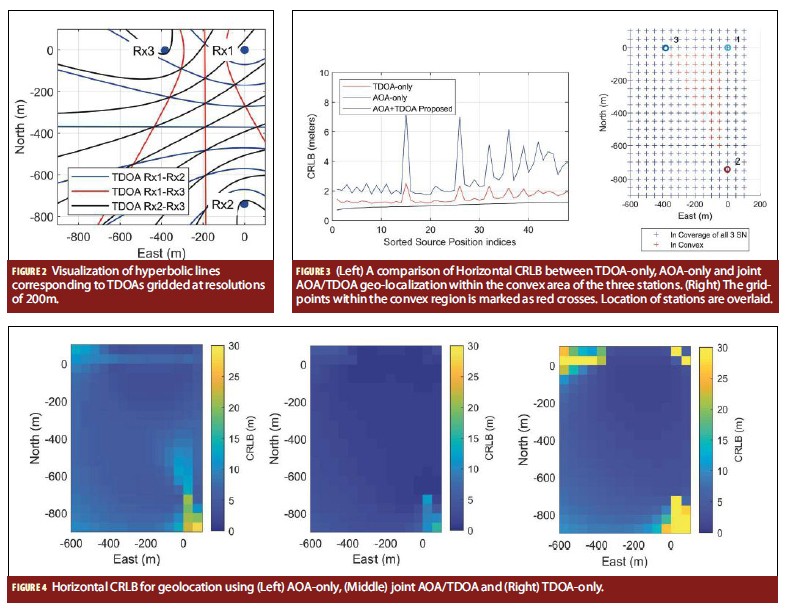
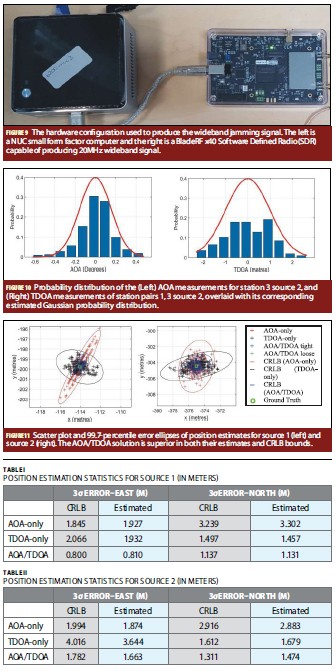
For this section, we intend to visualize the geometry-dependant accuracy of AOA-only, TDOA-only and our proposed AOA/ TDOA integrated solution over a realistic configuration of station baselines. We consider three stations in an ENU coordinate frame: (0, 0), (-2, -740) and (-383, -2). These coordinates correspond to the field trial configuration in the next section. In Figure 2, the superimposed geographical lines corresponding to a range of constant TDOA (iso-TDOA lines) spaced at 200 meters for a scenario with three stations is shown. An iso-TDOA line indicates the direction with zero gradient, hence the tangent to the iso-TDOA line is the direction with the greatest descent or greatest ascent.
For a fair comparison, it is important to assume appropriate measurement standard deviations that are realistic for both the AOA and TDOA systems in a convex region formed by three stations. The convex region corresponds to red grid points in Figure 3. For this section, we used AOA standard deviation of 0.3° and a time of arrival standard deviation of 1 meter as they are the worst case observed in our field test. For the following results, the effect of coverage is considered. Thus, the source location needs to be within 2 kilometers of a station for its AOA to be measurable and at least two AOA measurements are needed for AOA-only geo-localization, whereas TDOA can only be measured when the source location is in coverage of two stations and three stations are needed for TDOA-only geolocalization.
Figure 3 is produced by sorting the source’s position indices according to the CRLB of joint AOA/TDOA geo-localization and superimposing its corresponding AOA-only CRLB and TDOA-only CRLB. The superiority of joint AOA/TDOA estimation is obvious. The CRLB of either AOA-only or TDOA-only geolocalization within the convex region is within 2.0±0.5m and 5.0±3.0m, respectively as seen in Figure 3. In the same convex region, the CRLB of the joint AOA/TDOA geolocalization maintained within 1.0±0.3m. Hence, the AOA/TDOA geolocalization yields two major benefits. First, the CRLB at any point within the convex region will experience an overall reduction, in this case, a median of at least 50% improvement. Secondly, the stability of the positioning error within this region will have far smaller fluctuation; up to tenfold improvement in stability in this example.
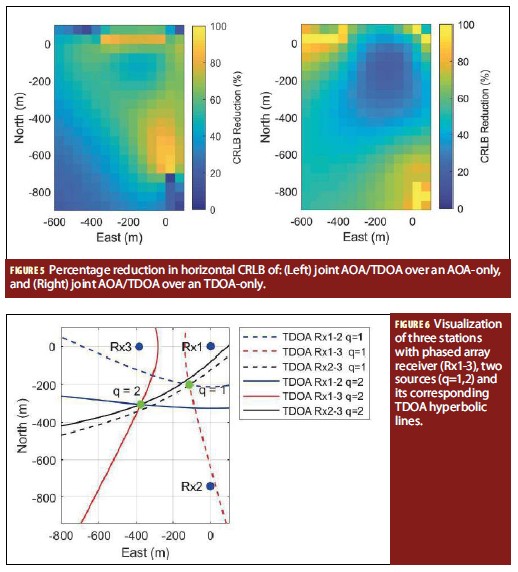
The horizontal CRLB of all three methods are shown in a colormap in Figure 4. Commensurate with Figure 3, these figures show clear improvements delivered by the joint AOA/ TDOA geolocalization.
The improvement, i.e. CRLB reduction, experienced when switching from an AOA-only geolocalization to a joint AOA/ TDOA geolocalization is shown in Figure 5. The percentage improvement peaks near the edges of the convex region where the AOA measured from a pair of stations have a difference of {0,π} radians. The joint AOA/TDOA geolocalization performs significantly better than AOA especially at these boundary points due the increased diversity in geometry when both AOA and TDOA measurements are considered for geolocation. From the TDOA-only geolocalization perspective, the joint AOA/TDOA geolocalization similarly yields an average of approximately 35% CRLB reduction within the convex region. This can be seen from Figure 5.
Field Test Result
We verify our proposed method against data collected from a specialised open area calibrated test range. The range is a remote site in southern Australia that permits actively monitored and
controlled transmissions of weak signal GNSS jamming & spoofing for experimental purposes. The 1 km2 range consists of three passive sensor arrays (each with a circular concentric array of eight element antennas, see Figure 7) as stations. As the sensor arrays operate in the GNSS band, it uses beam-steering to exploit the GNSS signal for calibration without being affected by the interference. This configuration is visualised in Figure 6. The positional inference from AOA measurements are not visualized here.
TThe stations are spread across three corners of the almost rectangular test range with local East-North coordinates (0.0, 0.0), (-1.9, -739.8) and (-383.1, -2.3). The station’s hardware was used to detect the occurrence of jammers and the computation of its AOA and TDOA measurements. It performs MUSIC processing of AOA measurements; whilst the TDOA measurements were computed via crosscorrelation of baseband signals.
In this field test in early 2017, we deployed two wideband jammers as stationary sources at GNSS-surveyed coordinates (-114.0, -199.8) and (-375, -304.5) for source 1 and source 2, respectively. The antenna is mounted on the two vehicles as depicted at the right of Figure 8. The GNSS antenna used for ground truth is shielded from the source’s antenna and is positioned at the null of the jammer antenna’s radiation pattern. Its RF cable is also guided away from source’s antenna before entering the equipment in the vehicle. The source transmitter is a BladeRF x40 (with a bandwidth of 20MHz) controlled by an Intel NUC small form factor PC running Linux.
Using the setup in Figures 7, 8 and 9, we collected 261 epochs valid of AOA and TDOA measurements from all three stations. These are logged from the GRIFFIN hardware which performs MUSIC processing for AOA estimation and cross-correlation processing for TDOA estimation in real-time.
We estimate the TDOA and AOA statistics from the dataset itself. The standard deviation of AOA for source 1 at stations 1, 2 and 3 are 0.05°, 0.12° and 0.30°, respectively. For source 2, those are 0.10°, 0.13° and 0.16°, respectively. The TDOA standard deviations for source 1 are 0.875m and 0.860m for the measurements between station 1-2 and station 1-3, respectively. For source 2, the TDOA standard deviations are 0.845 meters and 0.988 meters for the respective station pairs. An example for the gaussian fit on these measurements are shown in Figure 10.
The computed coordinates of the AOA-only geolocalization, TDOAonly geolocalization and the proposed AOA/TDOA geolocalization is shown in Figure 11. The scatter plot for both
sources show good agreement between the CRLB 3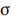
error ellipses and the empirical scatter points. Furthermore, the empirical scatter points for the proposed AOA/TDOA algorithm exhibited an equal degree of improvement as predicted by its theoretical CRLB error ellipse. More importantly, the geometry of the AOA (red) error ellipse and the TDOA (black) error ellipse is shown to complement each other to produce an improved accuracy for the joint AOA/ TDOA (blue) error ellipse.
The theoretical and empirical error statistics for the East and North component are shown in Table 1 and Table 2 for source 1 and source 2. The AOA and AOA/TDOA error statistics are highly commensurate with bounds dictated by the theoretical CRLB.
The minor discrepancy between the empirically measured 3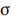 error and the theoretical 3 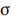CRLB can be attributed to minor diff erences between the modelled distribution of AOA and TDOA error and the actual AOA and TDOA error distribution (see Figure 10). Specifi cally, the empirical TDOA error statistics are unable to be correctly captured by a simple Gaussian model due to minor unmitigated timing variation and localised multipath eff ects.
From Table1 1, we can compute the empirical Euclidean 3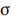 error for source 1 as 3.82 meters, 2.42 meters and 1.39 meters for AOA-only, TDOA-only and AOA/TDOA joint geolocalization. Th e corresponding errors for source 2 shown in Table 2 are 3.44 meters, 4.01 meters and 2.22 meters. RMSE reduction is empirically shown for the proposed AOA/TDOA method for source 1 to be at 63.6% from an AOA-only geolocalization and at 42.5% from a TDOAonly geolocalization. For source 2 the RMSE reduction is empirically shown to be ranging from 35.4% to 44.6%. These improvements are also commensurate with theoretical expectations as dictated by the CRLB.
While some of the features of the AOA/TDOA integration methods may enhance the positioning performance only in decimeters, they can be in the order of tens or hundreds of meters as the AOA and TDOA measurements
increase in error variance due to weaker transmit signal strength or greater geographical inter-station separation.
Application
While the scale of the RMSE enhancements are small in our fi eld trials, such improvements should not be underappreciated. To illustrate how our proposed method aff ect large scale deployment, we adopt the Kingsford Smith airport in Sydney, Australia as the scenario. The simulated stations are situated at (-1744, 2555), (1318, 1180) and (-32, -2262). As we only seek to understand the eff ects of geometrical variation, we base our TDOA and AOA measurements covariances to our fi eld trial data to compute the horizontal CRLB in this simulated scenario. Th e results are shown in Figure 12. Notice the signifi cantly enlarged contours of equi-RMSE for the joint AOA/TDOA method in comparison to the AOA-only or TDOA-only. Th e joint AOA/TDOA method also does not suff er from undesirable fl uctuation in accuracy as seen in the AOA-only method.
In absolute terms, the CRLB predicted RMSE are large because we have considered three stations over an approximately 3km x 5km coverage area, which is an order of magnitude larger than the coverage of our GRIFFIN open area test range. Also, the contours indicate the maximum CRLB. Actual CRLB near the center of the convex region of three stations are substantially smaller.
Conclusion
We have proposed a new integrated AOA/TDOA geolocalization algorithm that can be used for passively sensing and geolocating a wideband GNSS jammer and characterized its theoretical error distribution via Cramer Rao Lower Bounds. Also, we theoretically analyzed the proposed integrated AOA/ TDOA with realistic covariances in a hypothetical environment and found that this approach can deliver substantial reduction in root mean squared error (RMSE) over conventional AOAonly or TDOA-only geolocalization, when averaged across the entire test range. Additionally, we also show in a real-world experiment employing the GRIFFIN network of time-synchronized phased arrays that our proposed approach can deliver up to 63.6% and 44.6% of RMSE reduction when compared against AOA-only and TDOAonly geolocalization.
In absolute terms, our approach has delivered up to 2.43m reduction 3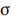 error in a real-world experiment, bringing the resultant horizontal 3 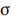error down to 1.39m. In our tests, the size of the approved GRIFFIN interference test range has limited our ability to test the case for stations spread across longer baselines. By way of extrapolation, our proposed methods can potentially deliver hundreds of meters of improvement in accuracy as visualised in a simulated deployment at an airport.
Acknowledgments
This work was jointly funded by the Australian Research Council (ARC) and GPSat Systems Industry through Linkage Project LP140100252. The field tests were supported by GPSat Systems Australia Pty Ltd.
Manufacturer
The stations used GRIFFIN prototype engineering hardware manufactured by GPSat Systems Australia Pty Ltd in early 2017 as supporting contribution for its ARC Linkage project with UNSW. The GRIFFIN hardware has since undergone substantial engineering changes. GRIFFIN is a series of hardware and software suite for detecting and geolocating jammers and spoofers in one or more GNSS spectrums. On 15 August 2019, the Australian Ministry of Defence announced that GRIFFIN is currently being taken into production via its Defence Innovation Hub program.
Additional Resources
See the online version of this article for references and papers cited.
Authors
Joon Wayn Cheong is a Postdoctoral Research Associate at the School of Electrical Engineering, University of New South Wales (UNSW) where he is currently investigating phased array signal processing techniques that can be used to geolocate harmful devices that can interfere with GNSS/GPS users. He received his PhD from UNSW in 2012 where he cracked the Locata pseudolite positioning system’s code and derived high-sensitivity GPS signal acquisition algorithms. He is the Technical Lead for UNSW’s Cubesat mission (named UNSW-EC0) and a ANUUSYD- UNSW three university joint-cubesat named I-INSPIRE 2. He developed firmware for the Namuru family of GPS/GALILEO spacequalified satellite navigation receivers.
Andrew G. Dempster received a Ph.D. from the University of Cambridge in 1995, in efficient circuits for signal processing arithmetic. He is currently a Professor with the School of Electrical Engineering and Telecommunications at UNSW and the Director of the Australian Centre for Space Engineering Research (ACSER). He was a System Engineer and Project Manager for the first global positioning system receiver developed in Australia in the late 1980s and has been involved in satellite navigation ever since.
Joe Fleming graduated as a Geomatics Engineer from University of Calgary 2000. In 2001, Joe joined the engineering systems team at GPSat Systems Aust. As the software manager he has led several key projects including AirServices Ground Based Regional Augmentation System (GRAS) which included 1.5 years contract time with Honeywell USA. More recently, Joe leads the development team continuing the evolution of precision positioning and navigation products for defence and mining applications.
Ming Zhu is a geomatics systems engineer in GPSat Systems Australia Pty Ltd. He participates in software and hardware design for a variety of customer geomatics related projects, including developing customised functions in GPS receivers via Application Programming Interface (API), real-time Global Navigation Satellite Systems (GNSS) simulation based on 3D engine and real-time terrestrial scanning. He achieved his Ph.D. degree in the School of Mathematical and Geospatial Sciences, RMIT University, Australia, in 2011 and has over 20 academic publications.
Graeme Hooper is the founder of GPSat Systems Aust P/L (1993), a company that delivers complex navigation engineering projects to defence, mining and aerospace. This is highlighted by the DST-Group CTD2014-2 project for deployable RF technology (GRIFFIN) continuously monitoring regional GPS frequencies, delivering rapid detection and precise geo-location for any RF interference Jamming and Spoofing activities. Graduated as an Electrical Engineer from Monash University 1980, he Joined Rockwell Int. 1987 as a defence GPS engineer commencing with two years in Cedar Rapids, Iowa on GPS Phase III User Equipment development.
