Design of a GNSS Acquisition-Aiding Signal

Working Papers explore the technical and scientific themes that underpin GNSS programs and applications. This regular column is coordinated by Prof. Dr.-Ing. Günter Hein, head of Europe’s Galileo Operations and Evolution.

Working Papers explore the technical and scientific themes that underpin GNSS programs and applications. This regular column is coordinated by Prof. Dr.-Ing. Günter Hein, head of Europe’s Galileo Operations and Evolution.

The structure of current GNSS open service signals is the result of a design trade-off between several performance figures of merit. The most relevant are position accuracy, receiver sensitivity (for signal acquisition, tracking, and data demodulation), and the time to first fix (TTFF).

Signal performance generally results from a compromise among those. However, if one concentrates on the signal acquisition phase, the last two factors assume a much higher relevance. Also, the design of the navigation message has to take into account many needs, and the information transmitted has to serve different services and/or classes of users. Again, of all the information present in a typical navigation message, only a portion is relevant to obtain the first position fix within a reasonable amount of time.

The main goal of the work described in this article is to propose the design of an acquisition-aiding signal and to discuss the benefits of adding such a signal to the current GNSS baselines.

Our work has focused on the Galileo E1 Open Service (E1-OS), but many of the concepts that we will introduce can be easily extended to any GNSS signal. The discussion presented here clearly does not pretend to be a proposal for an actual system implementation.

Signal Design
For the sake of simplicity, we refer to the new acquisition-aiding signal as E1-D. After an introduction to the overall approach used for its design, this section will consider various aspects of the E1-D, from the selection of the spreading modulation to all the elements related to data transmission, in particular the contents of the navigation message and the channel coding.

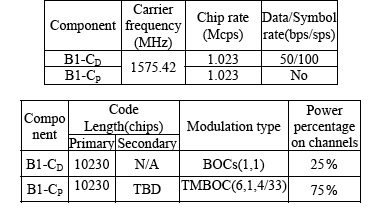
The design of a navigation signal must address several different factors, from the choice of the spreading modulation and of the PRN code characteristics to the design of the navigation message. As already anticipated in the introduction, a critical criterion for the choice of the spreading modulation involves the compatibility of E1-D with other existing signals in the band centered at 1575.42 MHz, both of the Galileo system and of other GNSSs. We also consider important criteria such as the correlation properties, multipath rejection, and ranging performance.

Selection of the PRN code length and the chip rate has to keep in mind that the E1-D component is intended to be an acquisition-aiding signal and, therefore, must guarantee that the acquisition is performed within a limited time interval. For this reason the code needs to be not too long, in order to limit the dimensions of the acquisition search space.

The important aspect of navigation message design and its channel coding — given the target of the E1-OS service — suggests that the signal should be characterized at the same time by a short TTFF and by sufficiently high data-demodulation sensitivity. We considered and analyzed several solutions, and the results are given in a dedicated section later on.

A final trade-off within the most promising alternatives has been realized taking into consideration the global performance for acquisition and data delivery, and a consolidated design is proposed as the first significant outcome of this work.

Spreading Modulation
The first fundamental criterion for designing a spreading modulation considers the radio frequency compatibility (RFC) within the newly introduced signal and those already present in the band. In our analysis, we assessed many possible modulations in terms of their effects on RFC.

In order to narrow down the possible choices, we needed a criterion of “acceptability.” For this purpose, we decided that an acceptable level of interference from E1-D would be no more than the same level of interference that nowadays is caused by E1-OS. Considering this criterion, we selected several possible spreading modulations.

Subsequently, we assessed the performance of the solutions that are acceptable from an RFC perspective with respect to several figures of merit, in particular the following: correlation properties, resistance against distortions due to the multipath effect, and ranging performance.

We considered binary phase shift keying (BPSK), sine-phased and cosine-phased binary offset carrier (BOC_sin and BOC_cos, respectively) modulations centered at E1 with a chip rate of [0.5,1]*1.023 MHz. As it will become even clearer later on, the limit on the chip rate is imposed by the fact that the signal needs to be acquired quickly and also that ranging accuracy is not the first priority. As for the sub-carrier frequency limit, this is imposed by the maximum allowed receiver bandwidth. For this, we considered the typical bandwidth of a Galileo E1-OS receiver as the limiting factor and, therefore, limited the sub-carrier frequency to 6.5*1.023 MHz.

Performing an RFC exercise within the main GNSS signals currently transmitted at the E1/L1 carrier frequency and signals modulated with the spreading modulations candidate for E1-D, we identified a subset of solutions satisfying these conditions:

• BOC_cos(0.5,0.5)
• BOC_sin(4,0.5) and BOC_cos(4,0.5)
• BOC_sin(4,1) and BOC_cos(4,1)
• BOC_sin(6.5,0.5) and BOC_cos(6.5,0.5).

The RFC analysis was performed in accordance with International Telecommunication Union (ITU) Recommendation ITU-R M.1831, which sets forth a methodology for RNSS inter-system interference estimation.

Another aspect that has to be mentioned when discussing compatibility is out-of-band (OoB) emissions. However, in the specific case of E1-D, we did not consider the issue of OoB emissions for two main reasons:

• no OoB emission requirements are available for the E1 band, e.g., no specific requirements are known to have been considered when Galileo E1 was designed, and therefore it is impossible to fix a requirement in terms of OoB that is coherent with the current signal baseline design
• the considered E1-D modulations are very narrow with respect to the total available bandwidth and consequently their impact in terms of OoB emissions on the global Galileo E1 signal are expected to be minor.

Performance Trade-Off and Sub-Selection
The properties of the correlation function comprise an important figure of merit that needs to be evaluated. As previously mentioned, E1-D is intended to serve as acquisition-aiding signal, and therefore it is crucial that the selected spreading modulation be characterized by a correlation function that eases the acquisition process.

As has been observed, the autocorrelation functions of the BOC_sin(6.5,0.5) and BOC_cos(6.5,0.5) modulations seem particularly questionable in terms of false-lock probability. Indeed, they are characterized by a very low first to secondary peak-to-peak ratio, as are the BOC_sin(4,0.5) and BOC_cos(4,0.5). Somewhat better is the case of BOC_sin(4,1) and BOC_cos(4,1), while clearly the BOC_cos(0.5,0.5) outperforms all the other solutions from the point of view of autocorrelation properties.

With respect to the distortions caused by multipath, the modulation displaying the poorest resistance to multipath has been found to be, as expected, that of BOC_cos(0.5,0.5). This is indeed the solution with the lowest chip rate and sub-carrier frequency. The signals producing the best performance under multipath conditions are the BOC_sin(6.5,0.5) and the BOC_cos(6.5,0.5), characterized by the lowest mean error, while the BOC_sin(4,1) and the BOC_cos(4,1) display better resistance to longer delay multipath due to their higher chip rate.

Looking at the code-ranging performance, the results that have been found are absolutely in line with that observed for the multipath rejection capability. Once again the best-performing modulations are the BOC_sin(6.5,0.5) and the BOC_cos(6.5,0.5), followed by the BOC_cos(4,1), the BOC_cos(4,0.5), the BOC_sin(4,1) and the the BOC_sin(4,0.5).

Summing up this evaluation, the two most interesting solutions are BOC_cos(0.5,0.5) and BOC_cos(4,1). The first has a very simple correlation function that makes it an ideal signal for acquisition aiding. The fact that the ranging and multipath rejection performance of the BOC_cos(0.5,0.5) are the worst among the candidates is of secondary importance, as the signal is intended mainly for acquisition. Any tracking would only take place with the aim of data demodulation, while users would not be expected to use it for ranging.

Meanwhile, the BOC_cos(4,1), this has on average the best performance, because it combines good compatibility performance with correlation properties and also exhibits good ranging and multipath rejection capabilities. We have discarded the BOC_sin(6.5,0.5) and the BOC_cos(6.5,0.5), despite their very good performance for ranging and multipath rejection, because of their poor correlation characteristics. The same applies for the cases of the BOC_sin(4,0.5) and the BOC_cos(4,0.5).

Navigation Message and Channel Coding Design
This section provides all the details on the design of the proposed E1-D navigation message and its channel coding. The articles by M. Anghileri et alia (2012) and M. Paonni et alia (2010) listed in the Additional Resources near the end of this article assessed the performance of the Galileo signals in terms of TTFF and its interrelationship with sensitivity performance. This performance reflects one of the major shortcomings identified in the Galileo E1-OS signal: the long wait time needed to retrieve the satellite ephemeris and system time data. One of the objectives of E1-D, therefore, is to overcome this problem by making available to the user the data necessary to achieve an initial position fix in the shortest time possible.

Another well-known problem of Galileo E1-OS is the fact that it employs a quite high symbol rate (250 sps) that allows user equipment to have a quite a short coherent integration time, thereby limiting receiver sensitivity. Together with improving the TTFF, a second requirement for the design of E1-D will be the one of improving the sensitivity, mainly by keeping the symbol rate as low as possible.

The basic concept that we propose to address this is to transmit, in addition to the system time, a set of reduced ephemerides in order to enable rapid signal acquisition, even if with an initially degraded ranging performance. This is a trade-off that mass-market GNSS users might tolerate. In order to simplify the generation of this new reduced set of clock and ephemeris data (CED) the article by M. Anghileri et alia (2012) proposes a very straightforward approach: rather than computing new parameters from scratch,the receiver signal-processing algorithm should take the broadcast CED that are already available in the satellites and obtain the new parameters by merely reducing the number of bits assigned to them.

A very simple, and at the same time effective, message design for an acquisition aiding signal would be to transmit orbit and clock parameters — already present in the I/NAV message of the Galileo E1-B data signal — in a compact version. The I/NAV message uses 428 bits to transmit orbit and clock parameters. As explained in the article by M. Anghileri et alia (2012), a compact set of CED can be sent within a block of 250 bits, still guaranteeing the minimum required performance.

Moreover, results presented in the referenced article and further analysis make us confident that one can also include the time of week (TOW) data within the 250 bits. For our purposes in this article, then, a block of 250 bits will be considered as the navigation message that the E1-D signal needs to transmit.

In order to guarantee the necessary protection of the data and making use of results presented in a related article by M. Anghileri et alia (2011), the following coding schemes have been considered for the design of the E1-D message: Galileo Convolutional Codes (CC) with a coding rate of ½, Turbo Codes with a coding rate of ½ and ¼, and Low Rate Convolutional Codes (LRCC) with a coding rate of ¼.

The need to guarantee the transmission of the desired data within a short time to improve TTFF requires us to shorten the redundancy (number of symbols per bit), and for this reason demands schemes with lower coding rates. For the same reason T_B, which corresponds to the time needed to transmit the whole block of length 250 bits, has to be kept as short as possible. For the design of the E1-D message, a maximum of 10 seconds has been allocated for T_B.

Considering the points discussed thus far, we have identified 10 possible E1-D solutions and measured their performance in terms of minimum carrier-to-noise density ratio (C/N₀) to demodulate the data. Table 1 gives the details of 10 alternative message-coding designs and their performance results.

The table provides results for both additive white Gaussian noise (AWGN) and land mobile satellite (LMS) channel models. The LMS results are provided for a user with a speed of either 5 or 50 km/h. The results have been obtained running the three-state LMS channel model for a suburban scenario and a satellite elevation of 40 degrees.

As can be seen in Table 1, the performance of the Turbo codes with a coding rate of ½ are always superior to those of the Galileo CC with the same T_B. Similar results appear for the Turbo codes with a rate ¼ versus the LRCC with the same coding rate. Given this performance data, we were able to make a first selection of the alternative designs, and from this point on we will only analyze the solutions based on Turbo codes. This means that the available solutions are:

• Turbo with coding rate ½, with T_B = 4, 5, and 10 seconds, which correspond to symbol rates of 125, 100, and 50 sps, respectively
• Turbo with coding rate ¼, with T_B = 8 and 10 seconds, which correspond to symbol rates of 125 and 100 sps, respectively.

Global Performance and Overall Trade-Off
In order to complete the design of the tool and make a choice within the various alternatives, we first needed to evaluate the global performance of the E1-D signal, focusing on the desirable characteristics of an acquisition-aiding signal — mainly a short TTFF and a high sensitivity.

Regarding TTFF performance, the most decisive factors are the following:

• chip rate and code length: those parameters are affecting the size of the acquisition search space, length of the acquisition process, and ultimately the acquisition time. In particular the product N ∙ T_c, where N is the length of the PRN code and T_c is the chip period, drives the total search space. The higher this product is, the longer will be the acquisition time, and therefore the TTFF;
• symbol rate: the inverse of the symbol rate represents the superior limit for the coherent integration time. The higher the symbol rate is, the shorter the maximum coherent integration time will be, and consequently the lower the maximum possible acquisition sensitivity.
• T_B: the longer the time needed to transmit the message, the longer will be the time to receive the data and, therefore, the TTFF.

Remembering what has been previously observed, it becomes evident that the last two factors are in opposition to each other. Among the alternative options presented in Table 1, those with a longer T_B are also those with a lower symbol rate, which improves the possibility of having a longer coherent integration time. At the same time, those are also the cases resulting in a lower data demodulation threshold.

Clearly this applies when considering the same coding rates. In our specific case, only coding rates of ½ and ¼ have been considered, again with the goal of not adding too much redundancy, which would also bring a higher symbol rate and therefore a lower sensitivity.

Sensitivity Analysis
Following the methodology presented in M. Paonni et alia (2009) cited in Additional Resources, Table 2 shows the minimum C/N₀ density ratios required to acquire, track, and demodulate a signal having one of the possible symbol rates of Table 1.

The acquisition sensitivity results have been obtained considering 10 non-coherent integrations, a detection probability of 0.9 and a false alarm probability of 10^-4. With respect to tracking, the results have been obtained assuming non-coherent tracking for both code and carrier, with loop bandwidth of 1 hertz for the delay locked loop (DLL) and 15 hertz for the phase locked loop (PLL). For the sake of comparison, Table 2 also shows the same computation based on the same assumptions for the case of Galileo E1-OS.

As can be seen, the values for the acquisition and (carrier) tracking sensitivity are in general higher than those enabling the data demodulation. In designing the E1-D signal, looking for very high data demodulation sensitivity is not useful if this is not supported by similar acquisition sensitivity values. At the same time, it remains very important to select a case with a short T_B in order to maintain a short TTFF. For this reason, among the various possibilities, the ones guaranteeing the lowest T_B have been considered, and therefore the Turbo with coding rate ½. The demodulation thresholds for these solutions are indeed already below the acquisition and tracking thresholds. So, considering solutions with a ¼ coding rate would have corresponded to longer T_B times without having effectively any advantage in terms of global sensitivity.

From the results shown in these two tables, one can see the benefits that E1-D would bring with respect to E1-OS. Case 3 (125 sps), for example, would correspond to an improvement of three decibels for acquisition sensitivity, one decibel for tracking sensitivity, and more than four decibels for data demodulation.

In light of the computations and results thus far, we performed a trade-off analysis among all the candidate solutions. Within the BOC_cos(0.5,0.5) and BOC_cos(4,1) the latter has been selected due to the faster chip rate and better RFC performance, multipath rejection, and ranging performance. A PRN code length of 1023 chips has been selected, in order to keep short the time to acquire the signal.

Within the coding options of Table 1, we selected Solution 2, which is characterized by a T_B of four seconds and employing a Turbo code with a coding rate of ½. In this way the T_B is much shorter than the one of I/NAV (30 seconds), and at the same time the symbol rate is kept to 125 sps, guaranteeing the possibility to have a coherent integration time up to eight milliseconds, with the previously described gain in sensitivity.

Table 3 summarizes characteristics of the designed E1-D signal and message.

Time-To-First-Fix Data (TTFFD) Analysis
The final element of our analysis aims to demonstrate the advantage that the introduction of E1-D would bring in terms of Time-To-First-Fix Data (TTFFD). This analysis has been performed following the methodology introduced in M. Paonni et alia (2010) and seeks to estimate the time needed to receive and demodulate the data needed for a first position fix.

The analysis has been performed for both the Galileo E1-OS and the E1-D signal as designed and described in the previous section. Figure 1 represents the cumulative distribution function (CDF) of the TTFFD for the E1-B and E1-D.

The plot of the TTFFD as a function of the delay for the E1-B and E1-D is represented in Figure 2.

Table 4 presents various metrics for the TTFFD for E1-B and E1-D extracted from the CDF results in these two figures. As can be seen in the previous table, the improvement brought by E1-D on the time to decode the data with respect to E1-B is very remarkable, resulting in a TTFFD four times shorter than the one of E1-B. Considering also the improvement in terms of sensitivity that has been observed in the previous section, we can conclude that the proposed E1-D acquisition-aiding signal as designed (Table 3) performs as desired.

Secondary Code Design
A fundamental point that needs to be tackled is how a newly introduced acquisition-aiding signal should assist the others already present in the baseline in terms of the necessary synchronization requirements that the acquisition aiding signal has to satisfy.

The secondary code of E1-D should address two objectives at the same time. First, it must achieve the bit synchronization needed to demodulate the data of E1-D. As indicated earlier, the primary code length has been fixed to 1,023, and therefore within one symbol the code is repeated eight times; the presence of a secondary code would solve this ambiguity and allow the bit synchronization in a very straightforward way. At the same time, recalling that E1-D is intended to be an acquisition aiding signal for the E1-OS services, we would like to use the secondary code to ease the hand-over from E1-D to E1-B and the E1-C pilot or dataless channel. For this reason we propose to put a secondary code of eight chips on top of the signal described in Table 3, with a chip period equal to one millisecond (that corresponds to one E1-D primary code), for a total length of eight milliseconds.

This secondary code can be used in a very straightforward way for the following cases:

• Bit synchronization within E1-D: The secondary code is used to locate the starting point of the symbols within the tracked sequence. Once the secondary code is aligned, the decoding of the symbols can immediately take place. The longest time to wait would be eight milliseconds, which would correspond to the length of one secondary code.
• Hand-over from E1-D to E1-B: Once the receiver is synchronized with the secondary code of E1-D it would be also aligned with the data symbols of E1-B. Indeed, within one E1-D secondary code are two E1-B symbols, and therefore the hand-over to the data channel of the OS service could be realized without any acquisition or re-acquisition. As a result, the receiver could immediately start to track E1-B and also decode the symbols and receive the accurate ephemeris and the other information contained within the I/NAV message.
• Hand-over from E1-D to E1-C: Again, once the receiver is synchronized with E1-D, it can begin tracking E1-C, too. If one wants to track the E1-C signal with a coherent integration time longer than four milliseconds, the secondary code should be aligned, as happens already for E1-C tracking.

Multiplexing E1-D within the Galileo E1 Signal
The following sections will examine the problem of how to multiplex this signal with the others already transmitted by Galileo in the E1 band. Currently, an interplex scheme is employed to multiplex together the E1-A, E1-B, and E1-C components within a composite constant-envelope signal.

The task of adding a further component is not trivial in terms of efficiency, especially considering the particular nature of Galileo’s composite binary offset carrier (CBOC) signal design. Indeed CBOC is a non-binary modulation, having four levels for both the data and pilot components. This being said, it becomes evident how everything comes down to multiplexing together six binary components: the PRS (E1-A), the four subcarriers of CBOC (BOC(1,1) and BOC(6,1) for each data and pilot code resulting in E1-B and E1-C, and the new E1-D to be added.

Within these multiplexing operations, majority voting and intervoting have been considered together with the interplexing. The main issue that arises is the multiplexing efficiency in light of the desired power split among the various components and the need for backward compatibility. This is a fundamental point, and all the solutions proposed here maintain backward compatibility, ensuring that E1-B and E1-C are placed on the I component and E1-A on Q. Additionally, the following power split ratios among the different components have been considered:

• ρ_OS/E1D = 3 dB
• ρ_OS/PRS = 0 dB

Moreover, considering the equal power share for E1-B and E1-C, in our proposed implementation the E1-D component ends up having the same power as either that of E1-B or E1-C.

Interplex
The interplex modulation (IM) presented for the first time in the article by S. Butman and U. Timor (Additional Resources) is a particular phase shift-keyed/phase modulation (PSK/PM) technique that combines multiple signals into a phase-modulated composite signal. IM has various implementations, two examples of which are the coherent adaptive subcarrier modulation (CASM) used in the GPS L1 band for the payload of the Block IIR-M satellites, and the modified interplex, that is the multiplexing scheme used for the Galileo E1 band.

We have developed a specific implementation for the E1-D study case with a very interesting result found for the Galileo E1 baseline: with the addition of an E1-D component, no power is wasted on the in-phase channel for intermodulation products. In general, the introduction of the IM signal results in a loss in terms of power, but at the same time it guarantees that the composite signal has a constant envelope. This latter characteristic is fundamental for transmitting the signal through the power amplifier of the payload without having AM/AM or AM/PM distortions.

Majority Voting
Majority signal voting is a technique used to multiplex different signal components in a composite signal to create a constant envelope. The technique is based on so-called majority logic combining.

As described in the article by J. Spilker, Jr., and R. Orr (see Additional Resources), the technique selects for transmission on a common carrier the value assumed by a majority of the component codes to be interplexed.

A more complex case, but also of greater interest from the point of view of navigation satellite signal design, is that in which the multiplexed signals are combined with different power levels. This approach requires the interlacing of chips from either the majority vote of the codes or any of the component codes themselves (which receive the name of solo chips). Thus, the code components are multiplexed in such a way that they can arbitrarily accommodate any power level.

The articles by the articles by J. Spilker, Jr., and R. Orr, and T. Fan et alia (Additional Resources) introduce two similar approaches aiming at adding a quadrature component to a majority-voted signal. Those techniques add a degree of freedom and make it possible to improve the transmission efficiency.

Starting from the results described in these two articles, the multiplexing scheme that we found to be the optimal solution interlaces the E1-D signal component sent on the I channel with a majority-voted signal and the solo chips of the BOC(1,1) components of the CBOC signal. A very interesting result here is that, in the particular case of the four components of the CBOC signal, the majority-voting logic could be applied to an even number of signals and result in a pure majority-voted CBOC signal.

Intervoting
Another promising approach that deserves attention for future application is the intervoting technique, presented in the article by G. Cangiani et alia. In intervoting, the majority voting and the interplex modulation are combined in a cascade of two blocks that capitalize on the most important advantages of both. Indeed, in the majority-voting logic unit, the components are multiplexed with lower power losses, and in the interplex modulator the power level between the signals are set more efficiently than in the majority-logic approach.

Making use of the results of the previous sections and considering the requirements in the terms of backward compatibility, the most convenient scheme for possible application of intervoting to the specific study case (E1-D) is the one represented in Figure 3 with:

• s_OSD,1 = D_OS(t)C_OSD(t)s_BOC(1.1)(t)
• s_OSD,1 = C_OSp(t)s_BOC(1.1)(t)
• s_OSD,6 = D_OS(t)C_OSD(t)s_BOC(6.1)(t)
• s_OSD,6 = -C_OSp(t)s_BOC(6.1)(t)
• s_E1D = D_E1D(t)C_E1D(t)s_E1D(t)
• s_PRS = D_PRS(t)C_PRS(t)s_PRS(t) 

where D_n(T) and C_n(T) are the materialization of the data message and of the spreading code of the n-component respectively.

All the signals have been implemented within a bit true simulator and the performance of the different techniques, measured and compared. Also, each composite signal realized with interplex, majority voting, and intervoting has been acquired, tracked, and processed with the standard SDR Galileo receiver mentioned earlier in order to demonstrate that all the solutions are effectively backward-compatible from the user perspective. The results of all those analysis are given in the following sections.

Multiplexing Efficiency Performance
The level of multiplexing losses introduced by each multiplexing technique represents a fundamental aspect that needs to be analyzed in order to understand the performance difference among the various possible solutions. The efficiency of a multiplexing algorithm can be defined in a very straightforward way as follows:

Equation 1 (see inset photo, above right)

Based on this definition, the results for the various options are provided in Table 5. The power levels have been measured after the modulation at IF, correlating the multiplexed signals (down-converted at baseband) with the baseband components.

This analysis implemented two different sets of power splits among the components, reflected in the table values, in order to show the dependency between the imposed power split ratios and the resulting multiplexing loss. The higher the power of the signal on the Q channel (here always E1-A) with respect to the power on the I channel, the more efficient the multiplexing scheme is. We can also observe that the efficiency increases with increasing the power split within E1-OS and E1-D, both transmitted on the I channel. With respect to the differences within the different algorithms, interplex is the most efficient, majority voting is the least efficient, and intervoting falls in between the other two.

We should point out that the inefficiency of the majority voting (and partly of the intervoting) in our specific implementation is due to the fact that the majority combining is applied here to the CBOC signal, for which the combined components are pairwise highly unbalanced (the power levels are 1/11 and 10/11 for the BOC(6,1) and the BOC(1,1), respectively). This is clearly penalizing the majority-voting approach that is well-known to perform best when the power spread among the components to be combined is not too large.

Signal Processing Results within a Standard SDR GNSS Receiver
In order to validate all what previously presented, the newly introduced signal has been processed with a software defined radio receiver for GPS and Galileo Open Service signals on the L1/E1 carrier frequency. The receiver, developed in Matlab, performs all the basic steps of coarse parallel acquisition, fine code phase and carrier frequency estimation, tracking, and navigation data bit decoding.

Coarse acquisition is implemented with a single-dimensional fast Fourier transform (FFT)-based approach. The fine acquisition improves the frequency estimation searching serially around the best estimate of the code delay. It also solves for the navigation data bit transition on GPS and for the secondary code phase on the Galileo pilot channel. Tracking uses a classical three-correlator (early-prompt-late) approach for GPS and a five-correlator (adding very early-very late) bump-jump approach for Galileo. The second- or third-order PLL and DLL adapt their bandwidth according to the tracking quality estimators, essentially the jitter of the discriminator outputs.

Verification of Backward Compatibility
The first analysis that we performed with the SDR receiver addressed one of the fundamental drivers for our design, namely, backward compatibility. From the receiver perspective the new composite E1-D signal is considered effectively backward-compatible if the legacy signals (namely E1-A, -B and -C) can be processed without any change in the receiver architecture and with comparable performance.

In order to verify that the new multiplexed signals are really satisfying this requirement, we used the software receiver to acquire and track the Galileo E1-C component from all the different newly designed composite signals (interplex, majority voting, and intervoting). The obtained results have been compared with what the receiver outputs when the legacy Galileo E1 signal is received.

In order to compare performance, a very straightforward figure of merit has been selected: the post-correlation C/N₀. Indeed, just comparing the estimated C/N₀ when tracking the E1-C component from the various baselines will enable us to understand whether the multiplexing techniques employed are introducing any losses and/or other issues at the correlation level, other than the ones already mentioned.

Following the approach described in the article by M. Pini et alia, we implemented three different C/N₀ estimators: signal-to-noise variance (SNV), the moment method (MM), and the classical narrowband-wideband power ratio (NWPR). The first is a coherent estimator, i.e., it relies on accuracy of the phase estimation, whilst the other two are noncoherent.

For GPS C/A and Galileo B and C components, the wideband integration time is fixed to one millisecond and the narrowband integration time, to 20 milliseconds (five Galileo symbols) in order to achieve consistent inter-constellation power-level measurements. The data channel coherent C/N₀ estimators are only valid for high C/N₀ as navigation data symbols are used to achieve the necessary coherent integration length.

On the Galileo E1-D component the wideband integration time is one millisecond, and the narrowband is eight milliseconds (the secondary code length). We adapted the NWPR formula accordingly, and the statistic leads to the same results as for the legacy signals with proportionally higher standard deviation. This is compensated by averaging over 200 milliseconds in all cases, which show comparable results.

The various signal baselines were generated with the same noise and signal power (normalizing the total power to the composite useful power). The three components (E1-B, -C, and -D) were acquired and tracked from all the signals and the C/N₀ estimated for the different cases. Figure 4 presents these results with Table 6 reporting the mean values. As can be seen, the three signal components tracked out of the three alternative composite signals realized with interplex, majority voting, and intervoting, respectively, produced results with almost the same C/N₀.

The minor differences within Table 6 are absolutely tolerable considering that the signals have been processed for just few seconds (five seconds in this specific case). Also, the slightly noisier estimate for the E1-D component is due to the shorter narrowband integration period (eight milliseconds).

Both the outputs of Figure 4 and the values of Table 6 refer to the NWPR estimates. The SVN and the MM estimators provided similar results, but we used the NWPR estimator, which settled to a stable value more quickly and therefore is more suitable for the quite short observation periods considered here.

The difference within the three signals and the Galileo legacy signal that can be observed in Table 6 is also absolutely consistent. In the case of the newly defined signals, each of the three components takes one-fifth of the total power, while in the legacy signal E1-B and E1-C get a quarter of the total, which brings us exactly to the one-decibel difference that appears in Table 6. In order to ensure complete backward compatibility, this gap has to be filled out on the transmission side by increasing the total transmitted power correspondingly.

E1-D Processing within the SDR receiver
The E1-D signal offers great flexibility in terms of signal processing options. Its modulation and data encoding allow the efficient implementation of acquisition and tracking policies in clear sky as well as in scenarios with degraded satellite signal availability.

With regards to acquisition, the one-millisecond–long primary code allows for double-block circular correlation in 500-hertz steps. A two-code long signal replica is needed in order to overcome the likely secondary-code (and/or navigation data symbol) transition, but the same holds true for a standard Galileo acquisition.

From a processing gain standpoint the BOC(4,1) modulation can be acquired and tracked as two separate BPSK(1) signals placed on its side-lobes. In either case, it is not critical to use a different center frequency as the sub-carrier offset can be embedded in the carrier recovery loop. Actually, in case of parallel in-frequency acquisition, the rotation of the signal’s discrete Fourier transform (DFT) can accomplish the demodulation in an elegant and efficient way.

In a stepwise implementation, acquisition would first be carried out at low gain and high speed to later gradually increase gain resulting in a longer scan time of all possible search bins.

If a correlation power loss of three decibels can be tolerated, then only a single side-lobe needs to be processed and twice as many bins can be processed in the same time. If more gain is needed, the secondary code can be used. Of course, the most straightforward method is to assume the combination of the two codes as a single eight-millisecond spreading sequence. The presence of navigation data bits requires the receiver to circularly correlate against 16 milliseconds of signal, which is expected to impose a significant computational burden.

Alternatively, the receiver can retrieve 16 one-millisecond cross-correlation arrays (spaced by 500 hertz) and re-combine them using a two-dimensional search of a zero-padded secondary code and 16 Doppler sub-bins. The final cross correlation matrix will have NxM dimension where N is the number of samples per primary code (one millisecond) and M is the number of 62.5-hertz frequency bins contained in the Doppler search space. The resulting processing gain in this latter case would be roughly nine decibels, which is higher than the legacy Galileo E1-B/E1-C case, with a corresponding improvement in acquisition speed.

The same agility offered by E1-D in the case of acquisition can be demonstrated for tracking. For strong signals, correlating one-millisecond codes and running a standard histogram-based secondary code alignment estimator will suffice. For a lower C/N₀ signal, if the secondary code ambiguity has not already been resolved during acquisition, an energy detector will leverage the presence of the good cross-correlation properties of the secondary code. The processing gain before and after secondary code alignment is shown in Figure 5 where the code discriminator output, the early/prompt/late (EPL) correlator output, and the time domain I/Q correlator output are represented.

Coherent integration of eight milliseconds allows higher processing gain compared to E1-B and naturally places the E1-D signal below the sensitivity achievable with a pure pilot signal.

In case of signals above 32 decibel-hertz, a single side-lobe can be tracked and symbols still retrieved from the navigation data. To achieve three decibels of further processing gain, two separate channels for each lobe can be recombined post-correlation with significant computational savings.

Once the synchronization with the secondary code has taken place, a smooth transition can be implemented at any point to E1-B. A reduction by 50 percent of the E1-C secondary code search space is also simultaneously achieved (as 8 milliseconds is not an integer divider of 100 milliseconds).

Conclusions
This article presented the proposed design of a GNSS acquisition-aiding signal. It discussed the specific implementation for the Galileo E1-OS case; however, most of the concepts presented here apply to any GNSS signal.

The different aspects to be tackled when approaching such a design have been discussed with trade-off analyses based on several performance key metrics. Particular effort was devoted to the design of the spreading modulation, the navigation message, and the multiplexing of the new signal within the Galileo E1 baseline.

For the choice of a spreading modulation, a key point was compatibility with the signals already present in the band. With respect to the message design, the concept of reduced ephemeris has been adopted in order to improve the time to first fix, while innovative channel-coding techniques have been considered in order to improve robustness and sensitivity. We discussed several possible approaches to multiplexing and analyzed their performance in terms of efficiency and backward compatibility with legacy receivers.

In order to have a complete understanding of the advantages and the challenges that the proposed design represents, we implemented an SDR receiver capable of fully exploiting the functionalities introduced by the acquisition-aiding signal and demonstrated the newly added signal processing. The obtained results clearly show the potential advantages that such a signal would introduce when processing the Galileo E1 Open Service signal, meeting the objectives of improving both the sensitivity and the TTFF of the E1 OS signal in a very flexible way.

Acknowledgments
The first part of the work dealing with the signal design has been accomplished at the University of the Federal Armed Forces in Munich within the European Space Agency (ESA) “Advanced Signal-In-Space Techniques (ADVISE)” Project. Implementation of the SDR receiver and the relative acquisition and tracking analyses were performed at the GNSS laboratory of the Institute for the Protection and Security of the Citizen, Security Technological Assessment Unit, within the Joint Research Center of the European Commission in Ispra (Italy). The tools and the SDR receiver used to obtain the results published within this article were programmed using MATLAB from the Mathworks, Inc., Natick, Massachusetts, USA. The contents of the present work reflect solely the authors’ view and by no means represent an official view of the European Commission or ESA.

Additional Resources
[1] Anghileri, M., and M. Luise, A. Perotti, A. Tarable, M. Paonni, B. Eissfeller, G. López-Risueño, and F. Zanier (2011), “A Fresh Look into Designing Channel Error Protection Codes for Satellite Navigation Messages,” European Workshop on GNSS Signals and Signal Processing, Toulouse, France, December 8–9, 2011
[2] Anghileri, M. and M. Paonni, E. Gkougkas, and B. Eissfeller (2012), “Reduced Navigation Data for a Fast First Fix,” Proceedings of Navitec 2012, Noordwijk, The Netherlands, December 2012
[3] Avila-Rodriguez, J.-A., and G. Hein, S. Wallner, J.-L. Issler, L. Ries, L. Lestarquit, A. de Latour, J. Godet, F. Bastide, A. Pratt, J. Owen, “The MBOC Modulation – A Final Touch for the Galileo Frequency and Signal Plan,” Proceedings of ION GNSS 2007, Fort Worth, Texas, 2007
[4] Butman, S., and U. Timor, Interplex – An Efficient Multichannel PSK/PM Telemetry System, IEEE Transaction on Communication, Volume 20, Is.3, Lune 1972
[5] Cangiani, G., and R. Orr and C. Nguyen, Methods and Apparatus for Generating a Constant-Envelope Composite Transmission Signal, International Patent WO02/28044 A2, September 2001
[6] Dafesh, P. and S. Lazar and T. Nguyen, “Coherent Adaptive Subcarrier Modulation (CASM) for GPS Modernization,” Proceedings of ION NTM 1999, San Diego, California, January 1999
[7] Fan, T., V. S. Lin, G. H. Wang, and P. A. Dafesh, “Study of Signal Combining Methodologies for Future GPS Flexible Navigation Payload (Part II),” Proceedings of the IEEE/ION PLANS 2008, Monterey, California, USA, May 6–8, 2008
[8] International Telecommunication Union (ITU), Recommendation ITU-R M.1831, “A coordination methodology for RNSS inter-system interference estimation,” 2007
[9] Paonni, M., and M. Anghileri, J.A. Ávila-Rodríguez, S. Wallner, and B. Eissfeller (2009), “Methodologies for the Determination of the Minimum Required Carrier to Noise Ratio to Receive GNSS Signals,” 4th European Workshop on GNSS Signals and Signal Processing, Oberpfaffenhofen, Germany, December 10–11, 2009
[10] Paonni, M., and M. Anghileri, J.-A. Ávila-Rodríguez, S. Wallner, and B. Eissfeller (2010), “Performance Assessment of GNSS Signals in Terms of Time to First Fix for Cold, Warm and Hot Start,” Proceedings of the ION International Technical Meeting 2010, San Diego, California, USA, January 25–27, 2010
[11] Pini, M., and E. Falletti and M. Fantino, “Performance Evaluation of C/N₀ Estimators using a Real Time GNSS Software Receiver,” Proceedings of the International Symposium on Spread-Spectrum Technologies and Applications, Bologna, Italy, 2008
[12] Rebeyrol, E., and C. Macabiau, L. Ries, J.L. Issler, M. Bousquet, M.L. Boucheret, “Interplex Modulation for Navigation Systems at the L1 Band,” Proceedings of ION National Technical Meeting 2006, San Diego, California, January 2006
[13] Spilker, J., Jr., and R. Orr, “Code Multiplexing via Majority Logic for GPS Modernization,” Proceedings of ION GPS 1998, Nashville, Tennessee, September 1998