Equations
EquationsGNSS is the technology of choice in most applications due to its dedicated infrastructure, Earth coverage, medium to high accuracy, and large market penetration. Most of the applications, including those we download on our smartphones, are in the category of Location Based Services (LBS). However, there are many other services and businesses that rely heavily on GNSS performance and reliability. For instance, Intelligent Transportation Systems (ITS) make extensive use of GNSS technology and this dependence will only grow in the future.
It’s not just that GNSS has become ubiquitous in our daily life, but many critical infrastructures worldwide have some sort of reliance on it. In addition to the already mentioned transportation systems, GNSS plays a significant role in synchronization in the power grid, high frequency trading operations, and synchronization of distant wireless communications towers.
This growing dependence on GNSS within critical (and non-critical) infrastructures has posed some concerns on the potential vulnerabilities of GNSS (see Amin et alia, “Guest Editorial: Vulnerabilities, threats, and authentication in satellite-based navigation systems,” in Additional Resources). As a consequence, there is a need for protecting GNSS against intentional and unintentional interference sources since disruption of GNSS can lead to catastrophic consequences.
The jamming threat, a specific form of intentional interference, is real and its occurrence has been documented in many occasions. Jamming devices are illegal in most (not all) countries, yet they are very easy and cheap to buy. Simple jammers can disrupt GNSS-based services in wide geographical areas (even in several kilometers), a fact that has certainly triggered research into anti-jamming techniques. Not only is jamming a threat, but other sources of unintentional interference can severely compromise GNSS performance.
This article aims at providing a discussion of classical mitigation techniques, while providing links to the field of robust statistics. This link provides a principled way of analyzing existing mitigation techniques, as well as conceiving new methodologies that rely on solid statistical principles. Purposely, we do not discuss interference detection techniques, leaving all the discussion to interference mitigation. Finally, the article introduces Transform Domain (TD) techniques and their robust versions, which are compared against time domain techniques using real data gathered in an experimental test.
The IC Principle
In this article, we are interested in both intentional and unintentional interference and, in either situations, the signal at the receiver antenna can be modeled as
y(t) = xθ(t) + i(t) + w(t) (1)
where xθ(t) is the legitimate signal, made of different components coming from the visible GNSS satellites, i(t) represents the interference signal, and w(t) is the random contribution of the thermal noise. Notice that xθ(t) is parameterized by θ, a vector containing the unknown parameters of the received signals such as their amplitude, time-delay, Doppler-shift, or carrierphase. For the i-th satellite signal, we define the parameters as Ai, τi, fd,i, and φi respectively. Roughly speaking, the estimates of θ are used to solve for the position at the receiver side. Most of the commercial jamming devices transmit rather simple periodic signals whose frequency is time-varying, fI(t). Therefore, a rather simple but general model is
i(t) = AI cos(2π(fRF + fI)t + φI) (2)
where AI is the amplitude of the interfering signal, fRF is the central Radio Frequency (RF), fI(t) is the time-varying interference frequency, and φI represents its phase. Depending on the behavior of fI(t) different jamming signals can be conceived such as Continuous Wave (CW) jammers when fI(t) = fI is a constant, or chirp-like jamming signals when fI(t) evolves over time following a saw-tooth pattern. Intuitively, the faster the variability and transitions of fI(t), the harder it is to mitigate interference at the receiver side. At the receiver, we are interested in digital signal processing methods to counteract interferences, therefore we assume that y(t) is sampled at a rate (fs = 1/Ts) satisfying the Nyquist criterion to yield its discrete-time version:
y[n] = xθ[n] + i[n] + w[n] (3)
A common approach to interference mitigation is to formulate it, statistically speaking, as an estimation problem. After detecting the interference, the set of unknown parameters characterizing the interfering signal needs to be estimated to enable Interference Cancellation (IC) at the receiver. A reconstructed version of the interference term, î[n], is subtracted from the observations such that a clean signal version is used afterwards by the receiver, ỹ[n] = y[n] – î[n]. The principle is depicted in Figure 1.
In the context of the standard operations of a GNSS receiver, IC can be better understood as the modification of the objective function in acquisition and tracking. Typically, GNSS receivers estimate the parameters of the received signals using a variety of methods that implement a Least Squares (LS) solution, where the input samples are compared with locally generated signal replicas. In particular, code delay, Doppler frequency and carrier phase are estimated as:
Equation (4) (see inset photo, above right, for equations)
Equation (5)
Notice that the subindex i denoting the satellite signal is hereafter omitted since we consider independent acquisition/tracking among satellites. c(·) denotes the spreading sequence for the satellite of interest and N the total number of samples used in the process. Cost function (5) can be minimized independently from A which can be estimated in a separate step. For this reason, the determination of A is not explicitly indicated in (4). In particular, it is possible to show that the minimization of (5) is equivalent to the maximization of the absolute value of the Cross-Ambiguity Function (CAF) defined as
Equation (6)
In the IC case, the cost function is modified after gaining knowledge of the interference. More precisely, the signal model is extended in order to account for the interference term and the cost function is rewritten as
Equation (7)
where î[n] is the reconstructed version of the interference, which requires detection and estimation as for Figure 1.
Using these definitions, the main IC techniques can be defined. For instance, a popular method for pulsed interference mitigation, due its simplicity, is pulse blanking (see article by Borio, 2016, Additional Resources). At a glance, pulse blanking detects the presence of interference by identifying abnormally large values in the pre-correlation samples. This can be easily achieved by comparing |y[n]| to a predefined threshold TPB. Then, the interfered samples are set to zero such that they are not used throughout the receiver. Mathematically, the estimated interference is
Equation (8)
which can be plugged in cost function (7) to understand how pulse blanking operates.
Robust Estimation
When the IC principle is used, the interfering term is treated as a signal component whose parameters should be estimated. A different approach for the design of interference mitigation techniques can be derived from the theory of robust statistics (see, for example, Huber and Ronchetti, Additional Resources). In this case, the receiver does not try to estimate the jamming signal but adopts processing strategies which can produce reasonable results even in the presence of interference.
The term “robust” is often used in the literal sense, in many cases just according to the definition provided by the dictionary. This has often generated confusion and algorithms defined as “robust” are not actually “statistically robust”. Robustness has to be intended here as a mathematical property of a system and can be assessed using rigorous criteria. An analogy can be made with the concept of Bounded Input Bounded Output (BIBO) stability: a system is BIBO stable if a bounded output is obtained for every bounded input. In a similar way, Qualitative Robustness states that a robust estimator is such that bounded departures from the assumed model do not cause it to provide aberrant results (see Hampel in Additional Resources). For instance, if an estimator assumes a Gaussian model for the observations, but outliers — which break the Gaussian assumption — are received and used, we expect the estimator to be relatively insensitive to them if claimed to be robust. For location estimators of the type
Equation (9)
i.e. that depend on a linear combination of input samples, y[n], processed by the non-linearity, ρ(·), robustness is obtained when ρ(·) is bounded. When pulse blanking is used, the CAF of the input samples is computed as:
Equation (10)
where, in accordance to (8), the non-linearity is
Equation (11)
is clearly a bounded function of the input samples. In this way, pulse blanking is not only a form of IC but is also a robust estimator for the CAF.
Although techniques implementing the IC principle can be robust, robust statistics provides, in general, a shift in the design paradigm for interference/jamming mitigation techniques. In particular, the focus is no longer in the definition of the most appropriate model for the interfering term, i(t), but on the search for robust procedures that allow the estimators to combat i(t) without actually estimating (or even detecting) it. A possible design strategy is to reformulate model (3) as
y[n] = xθ[n] + w′[n] (12)
where interference and noise are grouped together, with
w′[n] = i[n] + w[n]
In the robust estimation framework the goal is to adopt models for the aggregate term, w′{n}, which lead to robust estimators. In robust statistics, a model is considered as well, but its statistical assumptions are relaxed such that the estimators have some flexibility to process outlier measurements, which otherwise would make non-robust estimators diverge. In this respect, there exist several noise models which lead to robust estimators in classical robust statistical problems. It turns out that these models are also effective in the context of jamming mitigation in GNSS receivers. These models, which mainly characterize the statistics of w′{n}, include:
- Laplacian model: the aggregate noise term is assumed to follow a Laplace distribution.
- Cauchy model: the aggregate noise term is assumed to follow a Cauchy distribution.
- Student’s t model: the aggregate noise term is assumed to follow a t-distribution.
Other noise models could be considered for the design of different jamming mitigation techniques. Notice that, typically these distributions exhibit heavy-tail behavior, as opposite to the standard Gaussian assumption. From the aggregate noise model, robust mitigation techniques are finally obtained. We recently considered (see the paper presented by one of the authors at the 2017 European Navigation Conference and listed in Additional Resources):
- The usage of Zero-Memory Non-Linear (ZMNL) functions to pre-process the input samples.
- Non-linear correlators based, for example, on the median (which results from the Laplace noise assumption) and on the sample myriad (from the assumption of Cauchy noise).
The sample myriad is a location estimator, as the mean and the median, and it is defined, for real input samples, as
Equation (13)
where K is the linearity parameter of the Cauchy distribution (this is better explained in the following). A clear parallelism with the sample mean can be made: the mean is the argument which minimizes the sum of squares of the residuals, y[n]-μ. Additional details on the sample myriad can be found, for example, in the book by G. R. Arce listed in Additional Resources.
ZMNL functions can be directly obtained from the aggregate noise model as
ρ(y[n]) = –log f(y[n]) (14)
where f(y) is the probability density function (pdf) adopted to describe w′{n}. In this case, alternative versions of (10) are obtained by replacing ρPB(·) with ρ(·). In the ZMNL function case, the input samples are simply pre-processed using ρ(·) before being used by the standard correlator blocks. In this way, a robust CAF similar to (10) is obtained. In the second approach, it is recognized that the CAF is a weighted mean. The mean is inherently non-robust and thus, it can be replaced by robust operators such as the median and the myriad. For example, in the median case, the CAF in (6) becomes:
CR(τ,fd) = MEDIAN(y[n]c(nTs – τ)e–j2πfdnTs|n=0,1,…,N – 1). (15)
Note that the samples at the input of the MEDIAN operator in (15) are complex. In this case, it is assumed that two independent medians are computed on the real and imaginary parts of the samples. These approaches introduce significant robustness in the case of pulsed jamming and allow receiver operations even in the close proximity of a jammer.
Time, Frequency, Scale and All the Others
By representing the input samples in a different domain, an advanced class of interference mitigation techniques arises. A classic example is the usage of the Discrete Fourier Transform (DFT) and its fast implementation, the Fast Fourier Transform (FFT), to project the input samples, y[n], into the frequency domain. In this way, a new set of samples, Y(k), is obtained. Here, the index, k, is used to denote the set of discrete frequencies. The rationale of operating in a different domain is that, in such domain, the interfering term, i[n], admits a sparse representation. This implies that, I(k), the TD representation of i[n], is significantly different from zero only for a relatively small number of values of k. I(k) will thus appear as a set of pulses which can be easily blanked in the TD.
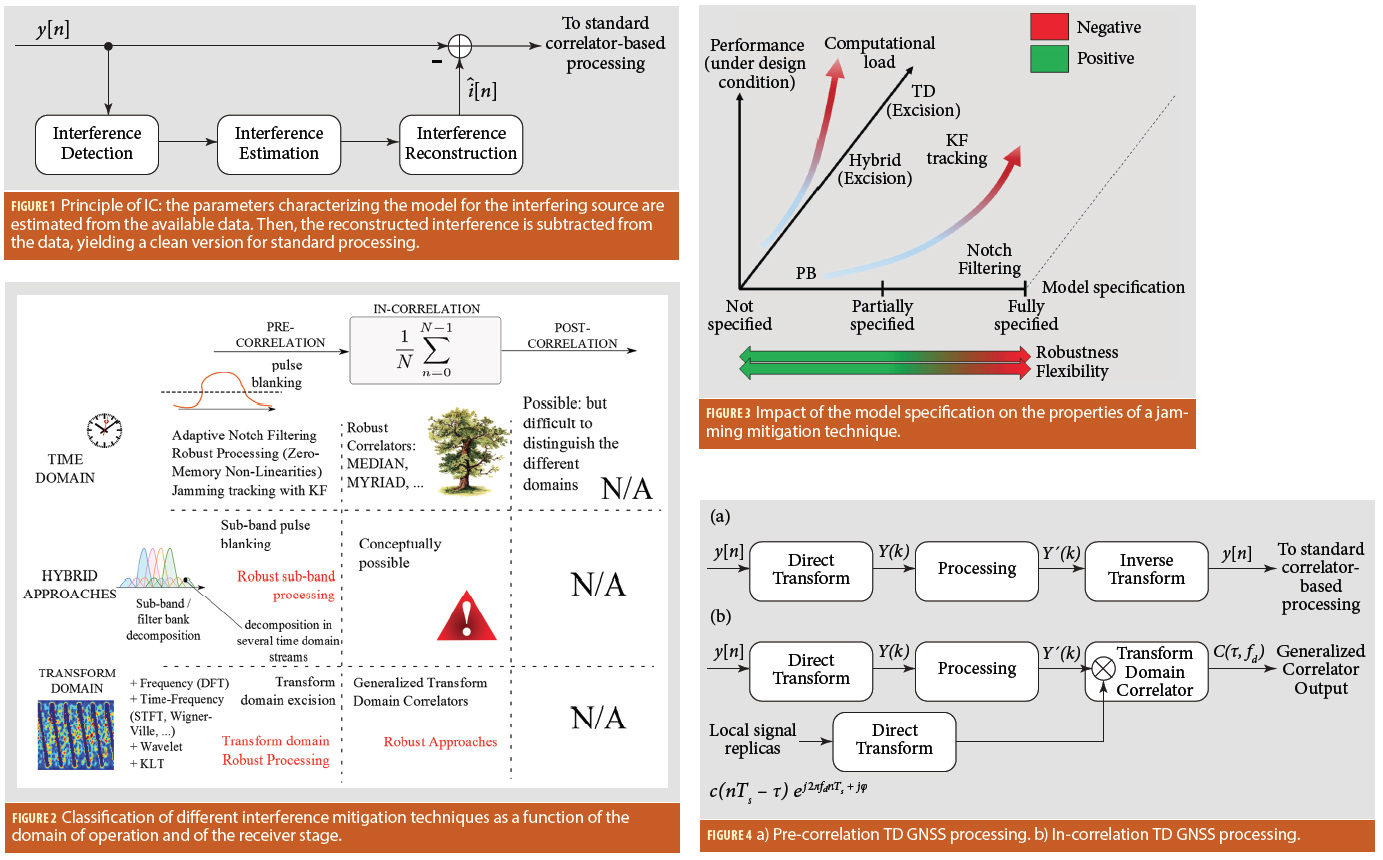
Depending on the domain of the transformation, it is possible to classify the different interference mitigation techniques as in Figure 2. The figure also takes into account the receiver stages where the techniques are actually implemented. In particular, interference mitigation techniques are classified according to their implementation with respect to the correlation operation as
- Pre-correlation: the algorithm operates before the correlation process takes place. In this way, mitigation is performed for all the processing channels at once and the characteristics of the useful received signals are not taken into account.
- In-correlation: mitigation is performed by modifying the standard correlation process.
- Post-correlation: mitigation is applied at the output of the correlators. In this case, different processing can be applied to the signals from different channels.
Time domain techniques are those that do not require a preliminary transformation to bring the input samples in a different domain. In this respect, adaptive notch filtering and pulse blanking are time domain techniques commonly used for interference mitigation, both implementing the IC principle. Adaptive notch filtering is an effective technique where the instantaneous frequency of the jamming signal is continuously estimated. The region of the spectrum occupied by the jamming signal is then removed through filtering. Although notch filtering performs the excision of a narrow frequency band, it is implemented using a recurrence equation in the time domain and thus it does not require a signal transformation. Alternative classifications can be adopted. Pulse blanking can be seen as a robust technique (as discussed earlier), whereas notch filtering is very sensitive to model mismatches. The notch filter can only operate if the interfering signal is instantaneously narrowband and if its center frequency is slowly varying with time. Other examples of time domain approaches used for interference mitigation are the usage of ZMNL functions, as described above, and the adoption of a Kalman Filter (see Mitch et alia in Additional Resources) to track and reconstruct the jamming signal. This latter approach is, in general, non-robust and sensitive to deviations from the model adopted for the design of the Kalman Filter.
Time domain pre-correlation techniques are, in general, low-complexity and approaches such as pulse blanking and notch filtering are now commonly implemented in professional and mass-market receivers. Time domain processing can be integrated with the correlator and, for example, robust correlators discussed in the previous section can be adopted. The complexity depends on the approach adopted. The median can be implemented in a quite efficient way and its complexity is comparable with that of the mean performed in standard correlators. The computation of the sample myriad requires an iterative procedure which can be computationally expensive.
Post-correlation mitigation techniques are not explicitly indicated in Figure 2. Techniques operating at this stage tend to be “mixed” in the sense that post-correlation information is used to drive pre-correlation processing. Moreover, after correlation, the input samples are significantly down-sampled and, for this reason, adoption of different domains is usually not considered. Remarkably, post-correlation techniques are typically ineffective in terms of jamming suppression, the main reason being that correlation with the local code causes a spread out of the (uncorrelated) interference, which makes it harder to be mitigated. Degradations in post-correlation products, such as the estimated Carrier-to- Noise power spectral density ratio (C/N0), can, however, be exploited for jamming detection.
In TD approaches, considered in the bottom row of Figure 2, the input signal, y[n], is projected into a different domain in the first place. These domains include frequency, with the usage of the DFT/FFT; joint time-frequency representations based, for example, on the Short Time Fourier Transform (STFT) or on the Wigner- Ville distribution; and joint timescale representations based on the Discrete Wavelet Transform (DWT). The Karhunen-Loeve Transform (KLT) has also been considered as a possible tool to obtain TD representations of the received GNSS signal, y[n]. Once in the TD, it is possible to apply techniques similar to those adopted in the time domain. TD excision is probably the most commonly adopted approach and it operates in a way analog to pulse blanking. If the absolute value of a sample in the TD is larger than a threshold, it is blanked and set to zero. Robust techniques can be also implemented in the TD, both at the pre- and in-correlation level. This topic is discussed in more detail in the next section. Although TD techniques are usually computationally demanding, several high-end professional receivers implement FFT-based algorithms and are able to perform interference detection and mitigation in the frequency domain.
In hybrid approaches the complexity of TD techniques is reduced using, for example, a bank of filters. The time domain signal is not transformed but split into several streams. Each stream is obtained using a separate filter which captures the content of the original signal on a specific frequency sub-band. This is a hybrid approach in the sense that each stream is a time domain representation of the frequency content of the original signal on a specific sub-band. Here, we referred to “frequency”, but other representation domains such as scale can be adopted for the design of the filter bank used for the signal decomposition. Approaches such as pulse blanking and the usage of ZMNL functions can then be implemented on the individual streams.
Finally, we would like to comment on spatial domain techniques, which can be used complementarily to the previously mentioned approaches. In this case, the time domain signal is not explicitly transformed but, instead, the signal is recorded using a multi-antenna receiver, which confers it with spatial discrimination capabilities. Conceptually, one can point to desired directions-of-arrival, while nulling the radiation pattern of the antenna at directions where an interference is detected. A detailed discussion is out of the scope of this article, but it suffices to say that pre- and postcorrelation techniques can be considered. Beamforming design can follow a plethora of options, being classified into temporal-, spatial-, or hybrid-reference beamforming techniques depending on the knowledge assumed for the desired and interfering signals. Typically, array processing techniques involve demanding computational resources and precise hardware designs.
Some general considerations on the properties of interference mitigation techniques are provided in Figure 3. In particular, the impact of model specification is analyzed. Strong model specifications reduce, in general, the flexibility and robustness of estimation methods to cope with (non-nominal) interference situations. This is the case of adaptive notch filters which can only deal with frequency modulated signals with slowly varying central frequencies. On the other hand, precise model specifications can significantly reduce the computational complexity of the technique and lead to optimal performance when the design conditions are met. For instance, notch filtering is computationally efficient and achieves performance comparable to that of TD techniques when dealing, for example, with CW interference.
TD techniques usually make only weak assumptions on the interference model. In particular, the underlying assumption is that the interfering signal admits a sparse representation in the TD. This corresponds to assuming that the interfering signals can be effectively described by a linear combination of few functions from a basis of the TD. For example, when the FFT/DFT is adopted, it is implicitly assumed that the interfering signal can be effectively described as the linear combination of few complex sinusoids. In general, weak assumptions on the interference model lead to flexible techniques which can operate in a wide range of conditions.
As a general principle, the increase of computational load should yield to performance improvements. When this improvement does not occur or it is limited, the mitigation technique should be re-considered. This phenomenon may occur for example when considering new TDs: the computational load of the transform required to project the input signal in the new TD might not be justified by the improvement of performance, for example, with respect to other TD techniques which can be implemented using fast algorithms such as the FFT.
Robust TD Approaches
Finally, we consider a new class of TD approaches which is based on the usage of ZMNL functions in the TD. More specifically, we assume that a linear transform, such as the DFT and the DWT, has been applied to the input signal and that the following TD samples have been obtained:
Y(k) = Xθ(k) + I(k) + W(k) = Xθ(k) + W′(k) (16)
Since linear transforms are used, the superposition principle applies and the different components in (12) have a corresponding term in (16). In particular, it is possible to identify the useful signal components, the interference term and the noise term. In this approach, we propose to model the received signal directly in the TD rather than in the time domain. In particular, we focus on different noise models for the aggregate TD noise term, W′(k). As discussed in the section on robust estimation, the model does not need to be accurate but should be selected in order to obtain robustness. In other words, in robust statistics, optimality is sacrificed in favor of robustness. In this case, we considered two non-Gaussian noise models: the complex Laplace and the complex Cauchy distributions for W′(k).
Following an approach similar to that developed for the time domain (see article by Borio, 2017, in Additional Resources), robust TD interference mitigation techniques can be obtained by processing the TD samples using a ZMNL function. Figure 4.a provides a schematic representation of TD approaches implemented at the pre-correlation level. The input samples are projected into the TD, processed and used to reconstruct a clean version of the time domain input signal, y′[n]. In the approach proposed here, the processed samples, Y′(k), are given by
Y′(k) = ρ(Y(k)) (17)
where ρ(·) is the non-linearity defined by (14). In this case, f(y) has to be interpreted as the pdf of the aggregate noise in the TD. If a Laplacian model is adopted, the following non-linearity is obtained:
Equation (18)
This implies that the TD components of the input signal are normalized by their amplitude and only the phase information is retained. Eq. (18) leads to a normalization of the different TD components: when frequency is considered, the spectrum of the output signal, Y′(k), has a constant unit amplitude. In this respect, the ZMNL function defined by (18) acts as a Zero-Forcing (ZF) equalizer. In common ZF equalizer implementations, however, several time samples are used to estimate the signal spectrum and determine the impulse response of the equalizer. In this case, a direct normalization is implemented in the TD. This, apparently simple processing, provides the receiver with remarkable interference mitigation capabilities.
Alternatively, if a Cauchy model is considered, the following processed signal is obtained:
Equation (19)
where K is the linearity parameter introduced in the robust estimation section when defining the sample myriad. This name is justified by the fact that K controls the “linearity” of (19): as K goes to infinity, non-linearity (19) becomes the identity. K should be set as a function of the variance of the non-interfered input noise. The determination of K is out of the scope of this paper.
Figure 4.b shows the in-correlator implementation of the TD processing. In particular, due to the Plancherel theorem, it is possible to show that unitary transforms preserve the scalar product and correlation operations. Examples of unitary transforms are the DFT and DWT (when properly scaled). In these cases, it is possible to compute the correlator directly in the TD. In some cases, this design choice allows significant computational load reduction. A well-known approach is, for example, the parallel code acquisition algorithm based on the usage of the FFT. In the parallel code acquisition algorithm, the FFT is already used for the computation of the correlators: the usage of nonlinearities in the frequency domain can be efficiently adopted without requiring additional operations.
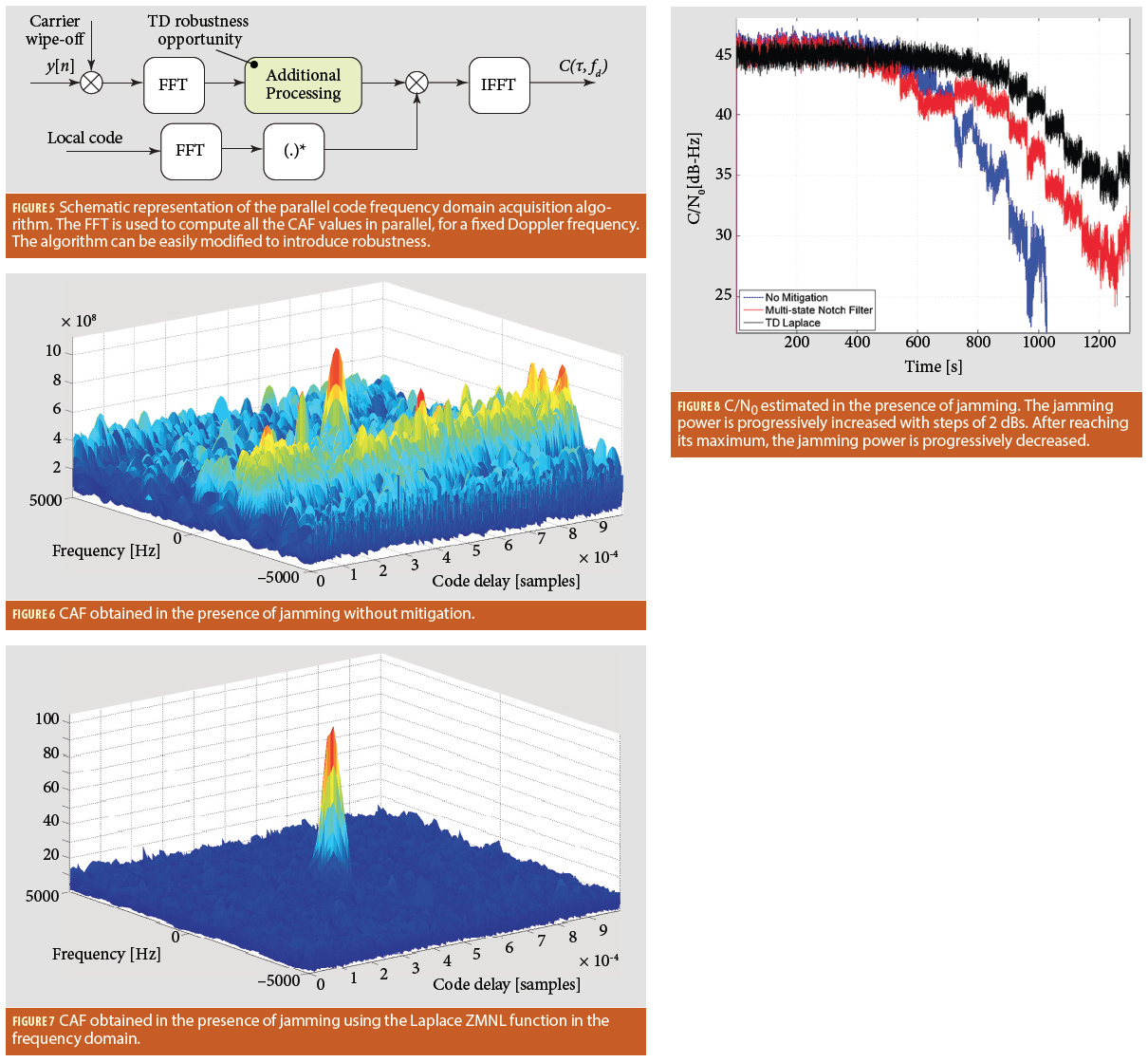
A schematic representation of the parallel code acquisition algorithm is shown Figure 5. As already mentioned, the algorithm foresees the transposition in the frequency domain of the input signal, y[n], thus it can be easily modified by introducing an additional processing block. This block is the light green box labelled “Additional Processing” in Figure 5. This block simply implements the ZMNL functions in Eqs. (18) and (19). In this case, robustness can be introduced with limited additional computational requirements.
In order to demonstrate the effectiveness of RTD approaches, we used the data available here and previously used to evaluate the behavior of an adaptive notch filter. The data contain a short dataset with GNSS data affected by jamming. In the archive, basic code allowing the acquisition of the GNSS signals present in the dataset is also provided. Without interference mitigation, it is not possible to detect the useful signal and the CAF shown in Figure 6 is obtained. Secondary peaks caused by the jamming signal are clearly present. RTD has been implemented by modifying the parallel code acquisition algorithm as indicated in Figure 5. Parallel code acquisition is implemented in the “DftParallelCodePhaseAcquisition.m” Matlab function and it is included in the archive indicated above.
Significant robustness can be introduced by adding a single line of code which implements normalization (18). We invite the readers to experiment with the code and add the following line of code
X = X ./ ( abs( X ) );
in the “DftParallelCodePhaseAcquisition.m” script. This line should be inserted in the “for” loop, before the computation of the inverse IFFT. With this modification, the impact of jamming is significantly reduced and it is possible to effectively acquire the useful GNSS signal. In particular, the CAF shown in Figure 7 is obtained: the signal peak clearly emerges from the noise floor and the secondary peaks due to the jamming signal are strongly attenuated.
The effectiveness of the proposed approach is further analyzed in Figure 8 which shows the C/N0 estimated for a signal affected by jamming under different conditions. In this experiment, the jammer was connected to a variable attenuator. The attenuation was progressively reduced leading to an increasing jamming power. In particular, the received jamming power was increased with steps of 2 decibels. This fact is reflected by the C/N0 values shown in Figure 8. After 1,200 seconds, the attenuation reaches its minimum value before being increased again. TD processing was implemented using the architecture depicted in Figure 4a and non-linearity (18) was adopted. TD processing significantly outperforms the notch filter used in Figure 8 for comparison. More specifically, a gain of more than 5 decibels is achieved for strong jamming signals. The considered notch filter implements interference detection and it is activated only when significant jamming power is sensed.
Conclusions and the Future of (Anti-) Jamming
Interference mitigation, in the context of GNSS receiver design, has been an active topic for research for several lustrums. It is likely to keep its good pace towards securing GNSS receivers — and the growing list of facilities and infrastructures depending on GNSS — from malicious jamming or unintentional interference. The field has indeed made substantial progress, mainly leveraging on advanced signal processing techniques. In this article we have covered classical time domain methods, but also discussed TD techniques that exploit sparsity of interference in other domains besides time. Additionally, the use of robust statistics was seen to provide interesting results and is a way forward for research. Anti-jamming is advancing, so are the capabilities of jammers to cause damage to GNSS receivers. Besides spoofing — which is probably one of the most complicated interference signals to generate — and jamming — probably the simplest — there is a middle ground. For instance, deceptive jamming, where a simple pulsed-jamming signal is disciplined to target specific parts of the navigation message. It was shown (see Curran et alia, “On the Threat of Systematic Jamming of GNSS”, Additional Resources) that deceptive jamming is not only feasible, but hardly detectable. It is foreseen that this, and other threats, will spur research in the area of antijamming.
Additional Resources
[1] Amin, M. G., P. Closas, A. Broumandan, J. Volakis, “Guest Editorial: Vulnerabilities, threats, and authentication in satellite-based navigation systems,” Proceedings of the IEEE, 104(6), pp. 1302-1317, 2016.
[2] Amin, M. G., X. Wang, Y.D. Zhang, F. Ahmad, and E. Aboutanios, “Sparse arrays and sampling for interference mitigation and DOA estimation in GNSS,” Proceedings of the IEEE, 104(6), pp. 1169-1173, 2016.
[3] Arce, G. R., Nonlinear Signal Processing: A Statistical Approach. Wiley-Interscience, Nov. 2004.
[4] Borio, D., “Swept GNSS Jamming Mitigation through Pulse Blanking” Proc. of the 2016 European Navigation Conference (ENC), Helsinki, Finland, June 2016, pp. 1-8.
[5] Borio, D., “Robust Signal Processing for GNSS,” Proc. of the 2017 European Navigation Conference (ENC), Lausanne, Switzerland, May 2017, pp. 150- 158.
[6] Curran, J. T., M. Bavaro, P. Closas, M. Navarro, “On the Threat of Systematic Jamming of GNSS,” Proceedings of the 29th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2016), Portland, OR, September 2016.
[7] Fernández-Prades, C., J. Arribas, P. Closas, “Robust GNSS receivers by array signal processing: theory and implementation,” Proceedings of the IEEE, 104(6), pp.1207-1220, 2016.
[8] Hampel, F. R., “A general definition of qualitative robustness,” The Annals of Mathematical Statistics, vol. 42, pp. 1887-1896, 1971.
[9] Huber, P. J., and E. M. Ronchetti, “Robust Statistics,” Wiley, second edition, February 2009.