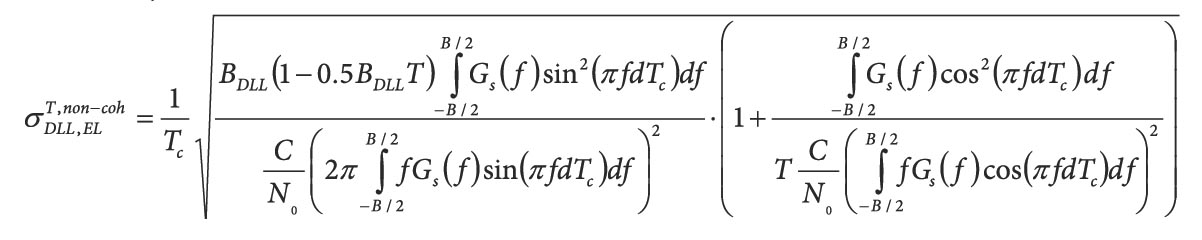
Four global navigation satellite systems are scheduled to be fully operational orbiting Earth in the coming years: the NAVSTAR Global Positioning System (GPS) from the United States, the GLObal NAvigation Satellite System (GLONASS) from Russia, the Compass/BeiDou-2 System (BDS) from China, and Galileo from Europe. A considerably high number of signals, coming from the satellites of those constellations, will share the radio electric spectrum.
Four global navigation satellite systems are scheduled to be fully operational orbiting Earth in the coming years: the NAVSTAR Global Positioning System (GPS) from the United States, the GLObal NAvigation Satellite System (GLONASS) from Russia, the Compass/BeiDou-2 System (BDS) from China, and Galileo from Europe. A considerably high number of signals, coming from the satellites of those constellations, will share the radio electric spectrum.
Moreover, some aeronautical radio navigation systems (ARNS) operate in the E5 Galileo band. For example, distance measuring equipment (DME) and tactical air navigation (TACAN) systems (both in the ARNS category) broadcast strong pulsed ranging signals that interfere with Galileo E5a and GPS L5 signals. As analyzed in the work by F. Bastide et alia, listed in the Additional Resources section near the end of this article, DME/TACAN interferences can severely degrade the receiver performance if left unmitigated.
Galileo receiver simulators are a powerful way to investigate the initial performance of Galileo receivers without the need of heavy measurement campaigns. Applications of open-source Galileo simulators, especially regarding the E5 band, are still hard to find in the current literature. This article presents the development of an open-source 64-bit Galileo simulator, including the acquisition and tracking parts and the interference mitigation blocks for continuous wave interference (CWI) and DME. The simulator is available on demand and upon agreeing to its open-source conditions (Details listed in the Manufacturers section at the end of this article).
This article thoroughly analyzes three narrowband interference mitigation methods explained in the next sections (notch filtering, zeroing, and pulse blanking) with Galileo E5a signals based on the open-source simulator created in our group (Signal Processing for wireless positioning group at Tampere University of Technology). The performance studies are done with both the benchmark CWI and the DME interferences.
The novelty of our work comes from analyzing jointly these three techniques with a practical Galileo simulator and from selecting the best method according to the interference type. We show that zeroing methods are best used for robustness and with strong narrowband CWI while pulse blanking methods are better than notch filtering methods for strong DME interferers. We also show that interferers with up to 10–15 decibels stronger power than the E5a signal power can be tolerated relatively well and that all considered approaches have relatively similar performance for medium strength interferers.
GNSS Interferences
Very simply put, GNSS interference can be defined as any signal, from any service, working in the same frequency as the satellite receiver. Wideband interference refers to interference with bandwidth comparable to or higher than the GNSS signal bandwidth, e.g., ultra-wideband (UWB) technology that transmits a huge amount of information with a very low power using a large bandwidth, inter-system interferences between satellites from different GNSSs, or intra-system interferences between satellites from the same GNSS (here Galileo). The spectrum is becoming overwhelmed by all the satellite systems deployed.
Some interference can be mitigated well using time or frequency processing methods. However, when dealing with wideband interference, the performance of these methods degrades, and additional processing has to be carried out, such as space-based processing methods (i.e., antenna array–based methods). Minimum variance distortionless response (MVDR) and minimum power distortionless response (MPDR) beamformers are some examples.
These spatial approaches are not assessed in this article, however, and we focused our research on narrowband interference — those whose bandwidth is much lower than the bandwidth of the GNSS signal of interest. Narrowband interference can be created, for example, by TV harmonics, inter-modulation products or signals from very high frequency (VHF) and ultra high frequency (UHF) stations, or signals generated by systems such as DME or TACAN. Figure 1 illustrates the different types of interference in Galileo bands.
Another criterion can be the intentionality. Within the unintentional interference group, we can emphasize: DME/TACAN, amateur radio, TV, surveillance radars, or wind profiler radars. Under the name of intentional interference (see Figure 2 and Figure 3), three different interference signals can be distinguished: jamming signals, which deliberately block or interfere with authorized wireless communications through illegal devices decreasing the signal-to-interference-plus-noise ratio (SINR); spoofing signals, which falsely imitate the signal-in-space (SIS) and may hack a targeted GNSS receiver; and meaconing signals, which are the interception and delayed-rebroadcast of actual GNSS signals.
In this article, we have simulated and studied two interference signals: CWI and pulsed signals such as those generated by the DME or TACAN systems. A CWI signal can be modelled as
Equation (1) (see inset photo, above right, for all equations)
where Δfcwi is the frequency offset with respect to the GNSS carrier, A is the CWI amplitude, and ϕ0 is the CWI signal initial phase.
Signals from air radionavigation systems, such as DME or TACAN, consist of Gaussian RF paired pulses. Pulse separation is 12 microseconds with each pulse lasting 3.5 microseconds. The maximum repetition rate is about 3,000 pulse pairs per second (pps).
DME systems are designed to provide service for 100 planes simultaneously and the transmitted power may vary from 50 watts to 2 kilowatts. A DME signal is typically modeled as:
Equation (2)
where α = 4.5 • 1011 s–2 is a parameter controlling the pulse width and Δt = 12 • 10–16 s is a parameter controlling the gap between paired pulses. The DME system operates between 960 and 1215 MHz; hence, it overlaps the Galileo E5 band.
Figure 4 shows an example of a DME signal in the time domain, its envelope, and its frequency spectrum.
State-of-the-Art Narrowband Interference Mitigation
Mitigation approaches can be categorized into two groups: time-domain and frequency-domain techniques. Time-domain mitigation techniques are those that make use of only mathematical calculation without any operation in the frequency domain. Heavy computational loads are avoided and complexity is lower. Non-linear methods, filtering methods based on convolution operations, or blanking methods are some of the proposed approaches in the literature.
Frequency-domain approaches are those based on signal alterations in the frequency domain. The article by A. Rusu and E. S. Lohan listed in the Additional Resources section near the end of this article presents a filtering method that exploits the cyclostationarity property using the spectral correlation function (SCF) and, therefore, can suppress additive white Gaussian noise (AWGN). Another, even simpler method is called zeroing, which is an excision-based method that we will explain in the next section.
The literature also presents various transformed domain mitigations that are worth mentioning briefly. One is the wavelet transform which is a time-scale representation technique that overcomes the common limit of fast Fourier transform (FFT) transformations using the short time Fourier transform (STFT), and another is the Gabor transform. Both of these methods separate useful signal and interference, removing the coefficients with high energy before the inverse transform. (These methods are described in articles by E. Anyaegbu et alia and K. Ohno and T. Ikegami, respectively, cited in the Additional Resources section.
Studied Mitigations. We selected the methods explained in this section based on the tradeoff between performance in acquisition and tracking and the method’s complexity, which in turn is directly proportional to the amount of computational load. The pulse blanking and notch filtering methods are time-based approaches, while the zeroing method is a frequency-based one in which the simulated signal is grouped into blocks that become suitable for FFT processing.
Pulse Blanking. This method is simple to implement: it blanks incoming signals that exceed a certain threshold, as illustrated in Figure 5.
The threshold can be chosen, for example, as a factor of the mean value of the absolute value of the received signal, i.e., γ = k • E(|s(t)|) with k optimized according to the interference. In our simulations, we used, for example, k = 3.5, chosen empirically. Figure 6 shows an example of pulse blanking performance in the frequency domain in the presence of a DME interferer.
Notch Filtering. Another time-domain method is notch filtering. A second order infinite impulse response (IIR) notch filter to mitigate the narrowband interference has been proposed, for example, by C. Ying-Ren et alia (see Additional Resources), based on the following transfer function:
Equation (3)
is the 3 dB filter bandwidth, and fI is the frequency of the interferer that must be canceled.
The interfering frequencies are searched in a recursive manner, based on a threshold, as illustrated in Figure 7. As an example, Figure 8 shows the spectrum of a GNSS signal affected by DME interference, with and without notch filtering-based mitigation.
Zeroing. The discrete Fourier transform of a sample GNSS signal s(n) can be written as:
Equation (4)
Narrowband interferences can be rejected just by zeroing the spectral samples above a certain threshold. This time, the threshold γFFT is obtained according to the mean and the variance of the absolute value:
Equation (5)
where ε is a parameter adjusting the threshold (in our simulations ε = 0.5). Figure 9 presents an example of the zeroing method (in the frequency domain).
Qualitative Comparison Among Narrowband Mitigation Techniques
Table 1 shows the strengths and weaknesses of each solution. Unlike the blanking approach, the zeroing and notch methods can be used for both CWI and DME interference. However, zeroing is much less effective than blanking against DME interference, and therefore it is not suitable for pulsed interference. The spread of the spectrum due to the steep variation in the time domain makes it more difficult to separate the useful signal from the DME signal. Some energy from the DME pulses remains after processing the signals employing the zeroing method.
Open-Source Simulator
The E5 Galileo band comprises two bands, an E5a band centered at 1176.45 MHz and an E5b band centered at 1207.140 MHz. The Galileo E5 signal is an AltBOC(15,10) modulated signal with a chipping rate of 10.23 Mcps. Figure 10 illustrates simulated and theoretical power spectral densities (PSDs) of an AltBOC(15,10).
Our team at Tampere University of Technology developed a simulator with which to analyze Galileo signals; Figure 11 illustrates an overview of this development. The simulator was initially started within the European Union’s Galileo Ready Advanced Mass MArket Receiver (GRAMMAR) project and is now offered via free licensing for research purposes.
The simulator implements the transmitted signal based on an AltBOC(15,10) modulation with a constant envelope signal, according to the Galileo Open Service SIS Interface Control Document (SIS-ICD). The signal is sent over a multipath channel with up to five Rayleigh fading paths; noise and interference are added inside the channel block.
Due to computing capacity, the signal is transmitted at an intermediate frequency (IF) of 20 megahertz. The down-sampling factor is applied before the channel is employed to reduce the simulation time. Because the processing of the E5a band is only carried out at the receiver, a lower bandwidth is needed. The E5a sampling rate in our simulator is 31.5 megahertz, while the transmitter sampling rate is four times higher. The interference generation block, included inside the channel simulation, is detailed in Figure 12.
The receiver includes the interference mitigation block, the acquisition, and the tracking unit. Figure 13 illustrates the interference mitigation block.
The acquisition block estimates the time and frequency initial values that are then fed into a tracking block. Figure 14 and Figure 15 show, respectively, examples of the time-frequency acquisition mesh without and with interference mitigation, in the case of a CWI interferer at 1176.45 MHz, i.e., an E5a carrier frequency.
The acquired signal is passed through a narrow correlator tracking block, including a delay lock loop (DLL) and a joint frequency lock Loop (FLL) – phase lock loop (PLL). Figure 16 presents the tracking unit block diagram.
Performance Comparison
We compared the performance of the mitigation techniques and present the results here in terms of detection probability at various carrier-to-noise (C/N0) levels. Figure 17 shows the acquisition performance in the presence of CWI for the zeroing and notch filtering methods (as the pulse blanking does not work for CWI cases). Figure 18 shows the acquisition performance in the presence of DME interference for the pulse blanking and notch filtering methods (as the zeroing method is not so suitable for DME interference). Both figures also show the situation without interference mitigation.
In order to achieve a high detection rate, the blanking method for DME pulses and zeroing method for CWI are the most effective techniques among those studied.
Regarding the tracking results, it is worth mentioning how large the tracking error can become if no mitigation is taken into account to deal with the interference. The acquisition threshold is selected based on the highest peak of the time-frequency mesh. (For further discussion of this point, see the article by E. Pajala et alia in Additional Resources.)
Due to some type of interference, for instance DME pulses, large fluctuations can appear at some point along this mesh, and as a result the initial values can be extremely large as Figure 19 shows. The computed position error could even be on the order of kilometers, due to the fact that the acquisition stage would feed an erroneous estimate into the tracking. However, as might be expected, the studied mitigations are able to keep this error within reasonable values as shown in Figure 20.
Conclusions
The main objective of our work has been to analyze the impact of CWI and DME narrowband interference on the performance of the E5 Galileo signal, and more specifically, E5a band when processed independently of the E5b band. We have implemented and evaluated three types of narrowband interference rejections, namely pulse blanking, zeroing, and notch methods. We have shown that the notch filtering has the worst performance among the three of them, while pulse blanking and zeroing methods are the best for DME and CWI, respectively (but none of them works for both interference types). We have also demonstrated that interferers with up to 10–15 decibels stronger power than the E5a signal power can be tolerated relatively well and that all considered approaches have relatively similar performance for medium strength interferers.
Acknowledgments
The authors express their warm thanks to the Academy of Finland (project 250266) and to the EU FP7 Marie Curie Initial Training Network MULTI-POS (Multi-technology Positioning Professionals) Grant No. 316528 for their financial support for this research work.
Additional Resources
[1] Abdizadeh, M., GNSS Signal Acquisition in the Presence of Narrowband Interference, Ph.D. thesis, Calgary University/PLANS Group, 2013
[2] Alonso de Diego, D., and N. G. Ferrara, J. Nurmi, and E. S. Lohan, “Simulink-Based Open-Source Simulator For the Narrowband Interference Mitigation in E5a Galileo Band,” Proceedings of the 5th International Galileo Science Colloquium, Braunschweig, Germany, October 2015
[3] Anyaegbu, E., and G. Brodin, J. Cooper, E. Aguado, and S. Boussakta, “An Integrated Pulsed Interference Mitigation for GNSS Receivers,” The Journal of Navigation, Volume: 61, pp. 239-255, 2008
[4] Appel, M., and A. Hornbostel, and C. Haettich, Impact of Meaconing and Spoofing on Galileo Receiver Performance, Institute of Communications and Navigation, German Aerospace Center (DLR), Oberpfaffenhofen, Germany, 2014
[5] Balaei, A., and B. Motella, and A. Dempster, “GPS Interference Detected in Sydney-Australia,” Proceedings of the IGNSS Conference, Sydney, Australia, 2007
[6] Bastide, F., and E. Chatre, C., Macabiau, and B. Roturier, “GPS L5 and GALILEO E5a/E5b Signal-to-Noise Density Ratio Degradation due to DME/TACAN Signals: Simulations and Theoretical Derivations,” Proceedings of the 2004 National Technical Meeting of The Institute of Navigation, San Diego, California, pp. 1049-1062, 2004
[7] Capon, J., “High-Resolution Frequency-Wavenumber Spectrum Analysis,” Proceedings of the IEEE, Volume: 57, pp. 1408–1419, 1969
[8] Dovis, F., “Recent Trends in Interference Mitigation and Spoofing,” Proceedings of the ICL-GNSS, Finland, 2011
[9] Gao, G. X., “DME/TACAN Interference and its Mitigation in L5/E5 Bands,” Proceedings of ION GNSS, Fort Worth, Texas, 2007
[10] Kang, C. H., and S. Y. Kim, and C. G. Park, “A GNSS Interference Identification using an Adaptive Cascading IIR Notch Filter,” GPS Solutions, Volume: 18, Issue: 4, pp.605-613, 2014
[11] Motella, B., and S. Savasta and F. Dovis, ”A Method to Assess Robustness of GPS C/A in Presence of CW Interferences,” International Journal of Navigation and Observation, Volume: 2010, Article ID 294525, 2010
[12] Musumeci, L., and F. Dovis, “Use of the Wavelet Transform for Interference Detection and Mitigation in Global Navigation Satellite Systems,” International Journal of Navigation and Observation, Volume: 2014, Article ID 262186
[13] Musumeci, L., and J. Samson and F. Dovis, “Performance Assessment of Pulse Blanking Mitigation in Presence of Multiple Distance Measuring Equipment/Tactical Air Navigation Interference on Global Navigation Satellite Systems Signals,” Radar, Sonar & Navigation, IET, Volume: 8, Issue: 6, pp. 647-657, 2014
[14] Ohno, K. and T. Ikegami, “Interference Mitigation Study for UWB Radio Using Template Waveform Processing,” IEEE Transactions on MTT, Volume: 54, Issue: 4, pp. 1782-1792, April 2006
[15] Pajala, E., and E. S. Lohan and M. Renfors, ”CFAR Detectors for Hybrid-Search Acquisition of Galileo Signals,” CDROM Proceedings of ENC-GNSS, 2005
[16] Rusch, L. A., and H. V. Poor, “Narrowband Interference Suppression in CDMA Spread Spectrum Communications,” IEEE Transactions on Communications, Volume: 42, Issue: 234, pp. 1969-1979, 1994
[17] Rusu, A., and E. S. Lohan, “Investigation of Narrowband Interference Filtering Algorithms for Galileo CBOC Signals,” Proceedings of the European Conference of Communications (ECCOM), Paris, France, 2012
[18] Rusu-Casandra, A., and E. Lohan and G. Seco-Granados, “Contributions to the Filtering of Narrowband Interferences in GNSS,” International Multidisciplinary Scientific GeoConference (SGEM), Albena, Bulgaria, 2013
[19] Rusu-Casandra, A., and I. Marghescu and E. S. Lohan, “Impact of Narrowband Interference on Unambiguous Acquisition Approaches in Galileo,” Proceedings of the International Conference on Localization and GNSS, pp. 127-132, Tampere, Finland, 2011
[20] Van Trees, H. L., Optimum Array Processing, Detection, Estimation, and Modulation Theory, Part IV, John Wiley & Sons; New York, New York USA, pp. 428–699, 2002
[21] Ying-Ren, C., and H. Yi-Cheng, Y. De-Nian, and T. Hen-Wai, “A Novel Continuous Wave Interference Detectable Adaptive Notch Filter for GPS Receivers,” Proceedings of the IEEE Global Telecommunications Conference, pp. 1-6, Miami, Florida USA, 2010
[22] Zhang, J., and E. S. Lohan, Effects and Mitigation of Narrowband Interference on Galileo E1 signal Acquisition and Tracking Accuracy, Proceedings of the ICL-GNSS, Tampere, Finland, 2011
[23] Zoltowski, M. D.. and A. S. Gecan “Advanced Adaptive Null Steering Concepts for GPS,” Proceedings of the 1995 IEEE Conference Record, Military Communications Conference (MILCOM’95), San Diego, California USA, pp. 1214–1218, 1995


