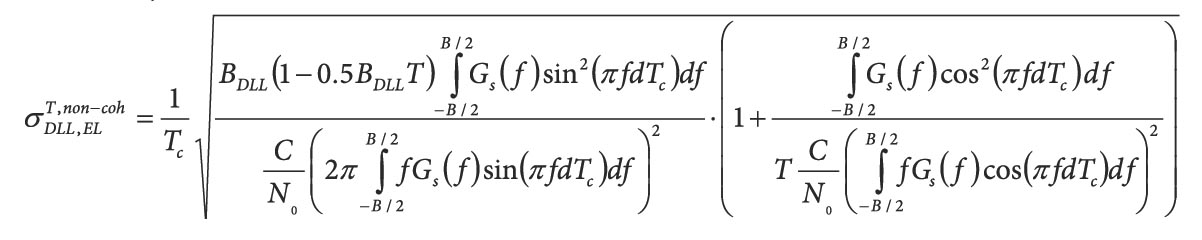
Working Papers explore the technical and scientific themes that underpin GNSS programs and applications. This regular column is coordinated by Prof. Dr.-Ing. Günter Hein, head of Europe’s Galileo Operations and Evolution.
Working Papers explore the technical and scientific themes that underpin GNSS programs and applications. This regular column is coordinated by Prof. Dr.-Ing. Günter Hein, head of Europe’s Galileo Operations and Evolution.
Nowadays a lot of alternatives exist for indoor positioning due to the recurring difficulties encountered by GNSS signals in such environments. However, because receiver performance and sensitivity are improving alongside GNSS signal availability, enough weak GNSS signals can already be detected and tracked reliably indoors to estimate a 3D user position.
Such high sensitivity receivers often make use of assisted GNSS (A-GNSS) to gather very weak signals. Once receivers are able to acquire and track these signals properly, further difficulties arise in the form of RF channel effects: for example, reflections, diffractions, and scattering. These fading effects must be modeled and parameterized correctly in order to make reasonable position and error estimates.
To assist the research and development process for innovative applications and algorithms, we have employed a GNSS reflectometry system to demonstrate the measurement of the deformation of the correlation function at L1, L5, E1, E5a, E5b, and E5ab (AltBOC) indoors. A previous article by J. Dampf et alia in the January/February 2013 issue of Inside GNSS described the reflectometry system design and operation. (See the Additional Resources section near the end of this article.)
The reflectometry system was adapted to investigate deformations in the GNSS signal correlation function. Knowing the shape of the correlation function in challenging environments can help engineers to understand and model signal behavior, providing a significant benefit for developing algorithms and applications. This article describes the tests and initial results that we have achieved.
Reflectometry System Design
The system uses a software receiver and open-loop tracking for the indoor channels, which are slaved to rooftop-based master channels so that we can measure extremely weak signals. Master and slave receiver share the same clock and, eventually, broadcast navigation data bits are removed from the slave tracking channel. This allows coherent integration times of tens of seconds (plus noncoherent integration) and thus the sensitivity is much below 0 dBHz.
The software receiver–based reflectometry measurement setup is able to:
- cope with all available civil GNSS signals in real time or post-processing
- support synchronization of two RF front-ends for a dual-antenna operation mode of up to four RF frequency bands simultaneously from each of the two antennas
- support channel slaving (open loop tracking) for carrier-only or carrier and code. (Slave channel offset parameters are adjustable.)
RF Configuration. The master front-end is connected to a roof antenna, and the receiver performs standard tracking. The slave front-end is connected to the static indoor antenna. The master channel assists the slave tracking channel by using the same numerically controlled oscillator (NCO) values to track the indoor signal.
The master channel outputs code and carrier pseudorange as well as the necessary prompt correlator values for later signal analysis. The slave tracking channel outputs multi-correlator values that are later summed up coherently and non-coherently. Figure 1 shows the RF setup. It is important to note that the two front-ends operate completely coherently based on the master front-end oscillator.
Generally, the receiver also allows real-time operation for multi-frequency reflectometry, but for our tests, data analysis in post-processing was more convenient.
Signal Processing.
In this section we will discuss the signal processing scheme of the software receiver and the main parameters of our methodology.
Master-Slave (Open Loop) Tracking. A common open loop tracking algorithm is used to steer the slave tracking channel. Herby the master channel keeps tracking the current signals. The master channel is responsible for estimating pseudoranges, Doppler, and provides NCO values for the slave channel. The slaved channel uses these NCO values to generate its code replicas. This allows for the placement of a multi-correlator around the prompt-correlator to later generate the plots of the deformed correlation function.
Figure 2 shows the general tracking channel structure. A switch indicates which NCO values are used. For the master channel the switch is set to (1) to use its own NCO values and the slave channel switch is set to (3) to use the NCO values from the master.
Multi-Correlator. The multi-correlator grid can be adjusted for each signal type. In our current investigation, we are interested in the multi-correlator values at zero Doppler offset while ignoring other Doppler bins. This is reasonable as the indoor antenna is static. Table 1 lists the correlator range and the spacing for the analyzed signals.
The output of the tracking channels is saved in scientific ASCII log files, including such necessary information as prompt and multi-correlator values. We can derive the correlator function from these values.
Extend Coherent and Noncoherent Integration. The files with stored correlator values are read in with MATLAB. The first step is to synchronize the prompt correlator values from the master channels with the multi-correlator values from the slave channels. This must be done because the multi-correlator output from the slave channel starts later due to the need for the master channel to first be locked — only afterwards can the hand-over to the slave channel be performed.
The multi-correlator values Pt;islave;raw for time epoch t and the multi-correlator code phase index i still contain all phase dynamics from the satellite movement and receiver/satellite oscillator jitter. They also possibly contain present data bits and the secondary code. These phase dynamics and the data bits/secondary code are removed from the multi-correlator values by subtracting the phases of the prompt correlator Ptprompt of the continuously tracked master channels. This is written as:
Equation 1 (see inset photo, above right)
Once the phase dynamic is removed, the phase stays relatively constant. The only phase changes are due to the different location of the two antennas and due to changes in the indoor environment, which is illuminated by the satellites at different elevation angles, which slightly changes the multipath reflections over time. This makes long coherent and non-coherent summation intervals possible. We should also note that the cross-correlation effects between different GPS C/A-code signals are mitigated due to the stochastic independence of the navigation data bits for different satellites.
Equations 2 & 3 (see inset photo, above right)
Measurement Results
Three different static measurements have been performed at the Lustbühel observatory in Graz/Austria (47°4’2” North, 15°29’36” East). The observatory consists of three floors. The measurements were performed at the first (lower, Figure 3) and second (middle, Figure 4) floors.
At each measurement point, we recorded streams of GPS L1/L5 and Galileo E1/E5a/E5b samples. We decided to start the measurements at a less challenging location in a window on the second floor, numbered 1 in Figure 4. The second measurement was performed at a center point of the second floor indicated with a 2 in Figure 4, and the third measurement at a central point on the first floor, indicated with 3 in Figure 3. The receiver itself was located near point 2. We moved the indoor antenna around tethered to a 50-meter long RF cable.
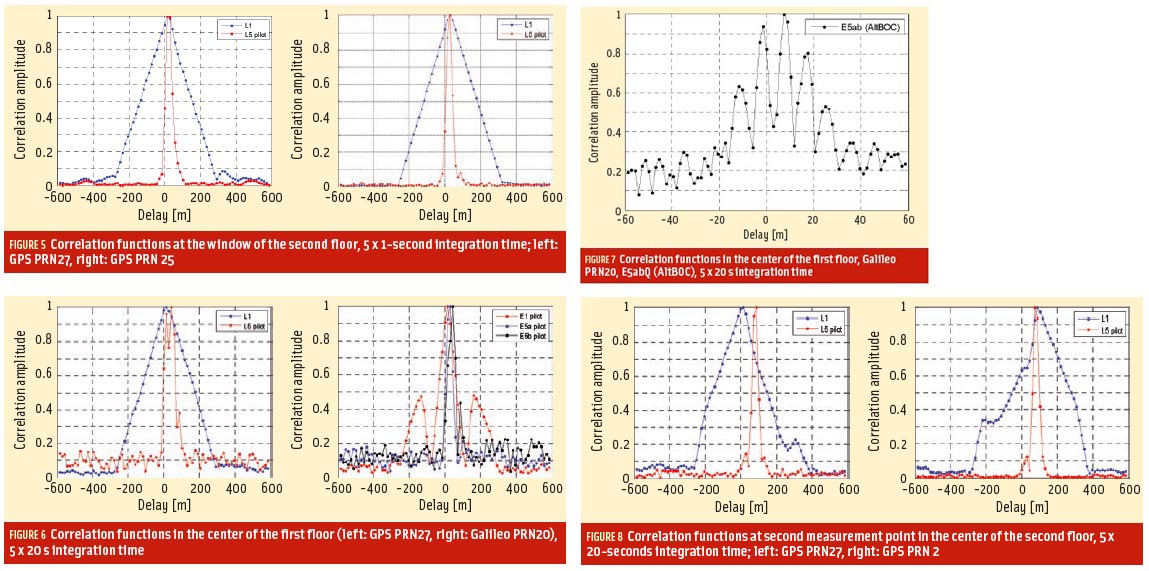
When looking at the results in Figure 5 obtained at the second-floor window where the antenna has more or less a clear line of sight to the satellite (apart from some canopy), one sees that the correlation functions for GPS L1 and L5 have more or less a triangular shape. The peak is for both frequencies at approximately the same delay. This delay is the projection of the baseline vector between the roof-top and window antennas in the satellite direction. (One antenna is closer to the satellite than the other) plus hardware delays (long RF-cables!).
Synchronization delays between the two RF frontends are below 14 centimeters and can be ignored. This test and its results basically validate the measurement setup.
Figure 6 presents the measurements at Point 3 for one GPS and one Galileo satellite. Both satellites had an elevation of around 20 degrees. Due to the attenuation of the GNSS signals, the integration time has been increased to 5 coherent sums of 20-second duration. By doing so, the received signal is brought well above the noise floor. We tried further increases in integration time, but these did not improve the results.
For the GPS satellite, one clearly sees how the L5 correlation function broadens, indicating severe multipath effects. One can identify three peaks in the L5 function and the left-most coincides with the L1 correlation peak. The L1 correlation function looks relatively undisturbed. The Galileo correlation function on E5a and E5b broaden also, but the peak positions differ on E5a and E5b (and both are different than E1). This would indicate a frequency dependence of the multipath effects.
The software receiver uses a post-correlation scheme to combine E5a and E5b correlation values to obtain the full AltBOC signal. This combination scheme also works for reflected signals. Interpolation allows us to achieve a much finer code phase resolution. Figure 7 shows the same measurement as Figure 6 but shows the AltBOC correlation function instead.
We noticed that the AltBOC correlation function is much more sensitive to the integration parameters. Eventually the multipath effects may cause the different AltBOC lobes to cancel each other, such that for certain integration parameters the AltBOC structure is destroyed. This is not the case for Figure 7 where the narrow (i.e., accurate) main peak of the AltBOC is visible.
A more complex behavior has been detected at Point 2 (Figure 8). First of all, we noticed the presence of significant RF tone interferers on L5, eventually determined to have been caused by nearby printers. This should not degrade the performance of the correlation function.
Looking at the GPS L1/L5 correlation functions, a very rich structure can be identified. L1 and L5 correlation peaks are separated by nearly 80 meters for PRN27 and the L1 correlation functions are severely distorted. We could not determine what may have caused this structure, but notice that such signals obviously would present a large challenge if used for indoor positioning.
Summary
A reflectometry system is an ideal tool to study the characteristics of indoor signals. As it is able to remove satellite dynamics, receiver oscillator jitter, and navigation data bits from the indoor signals in a nearly perfect way, the integration times can be extended almost infinitely and even the weakest signals can be measured. Tracking the same satellite on multiple frequencies allows for cross-checking of results. In our tests, we saw correlation functions ranging from nearly undistorted signals to extreme deformations. Generally, we could verify that L5 and E5 will boost indoor positioning significantly.
Acknowledgments
The authors would like to thank the staff of the Institute of Space Research of the Austrian Academy of Science (especially the satellite laser ranging team) for their hospitality during the measurements.
Additional Resources
[1] Dampf, J., and T. Pany, N. Falk, B. Riedl, and J. Winkel, “Galileo Altimetry Using AltBOC and RTK Techniques,” Inside GNSS, January/February 2013, pp. 54-63
[2] Hein, G., and M. Paonni, V. Kropp, V., and A. Teuber, “GNSS Indoors: Fighting the Fading — Part 1,” Inside GNSS, March/April 2008, pp. 43-52
[3] Hein, G., and A. Teuber, H. J. Thierfelder, and A. Wolfe, “GNSS Indoors: Fighting the Fading — Part 2,” Inside GNSS, May/June 2008, pp. 47-53
[4] Hein, G., and A. Teuber, “GNSS Indoors: Fighting the Fading — Part 3,” Inside GNSS, July/August 2008, pp. 45-53
[5] Pany, T., and N. Falk, B. Riedl, T. Hartmann, G. Stangl, and C. Stöber, “Software GNSS Receiver, An Answer for Precise Positioning Research,” GPS World, Vol. 23, No. 29, September 2012