 Figures 1-3
Figures 1-3Working Papers explore the technical and scientific themes that underpin GNSS programs and applications. This regular column is coordinated by Prof. Dr.-Ing. Günter Hein, head of Europe’s Galileo Operations and Evolution.
Working Papers explore the technical and scientific themes that underpin GNSS programs and applications. This regular column is coordinated by Prof. Dr.-Ing. Günter Hein, head of Europe’s Galileo Operations and Evolution.
During the past two decades, global navigation satellite systems (GNSS) have become an integral part of many critical infrastructures, including energy transmission and distribution, telecommunications, financial services, and transportation. An ever-growing dependence on GNSS inevitably creates incentives for adversaries to target GNSS with the intention of causing damage and disruption or to obtain an illegitimate advantage.
Improving the resiliency of navigation and timing can potentially be achieved through a combination of system and user-level techniques, providing protection of both navigation message and ranging level. This article introduces the fundamentals and various objectives of GNSS authentication. The focus is on protection of the navigation message and various schemes for providing assurance of its authenticity and cryptographic integrity. This is commonly referred to as navigation message authentication (NMA) [1].
In this article, we will first introduce the objectives of GNSS authentication and describe the concept and the design drivers for NMA. Next we will present various NMA schemes based on one-way functions and discuss key management considerations for NMA. Finally, we will makes some observations about the pros and cons for different classes of NMA approaches.
Fundamentals of GNSS Authentication
GNSS authentication can be divided into two major tasks:
- Navigation data protection enables the receiver of a message to determine whether it originates from its claimed sender (i.e., data authentication) or if it has been maliciously forged, and whether the observed message has been maliciously modified during transit (i.e., data integrity protection).
- Range measurement protection allows the receiver of a ranging signal to determine whether it originates from its claimed sender or if it has been maliciously forged (i.e., source authentication), and to ensure that the measured time of arrival (TOA) has not been maliciously altered.
Notice that in this article, the term integrity has a security-dictionary meaning (i.e., cryptographic integrity) and not to the risk of a position error exceeding a protection level or an alert limit.
We can summarize the types of attacks on the navigation function as follows:
- data-level attacks that have the goal of inducing a receiver to use wrong navigation message in the position/velocity/time (PVT) computation. This could be carried out by data forging or modification in which an attacker generates arbitrary navigation data or modifies the original data, or data replay
where the attacker retransmits old data for which a newer version is available, for the purpose of intentionally degrading the output of the navigation function.
- ranging-level attacks that have the aim of inducing the receiver to use wrong ranging measurements in the PVT computation. This could be carried out by signal forging whereby an attacker generates arbitrary navigation signals, or signal relay when the attacker records and rebroadcasts the entire RF signal modulated with unchanged code and data. In radar and satellite navigation domain this attack is known as meaconing, or wormhole attack for ground wireless protocols.
Furthermore, we should note that the aforementioned classes of attacks can be combined. For instance, it is possible to forge a signal (i.e., spoofing the ranges) that conveys true navigation data (i.e., data replay). For a more comprehensive analysis on the vulnerabilities of GNSS, readers can refer to the article by R. Ioannides et alia listed in Additional Resources. We can address the challenge of protecting the data level by using authentication techniques applicable to the information security domain, while the problem of protecting the ranging level belongs to the domain of signal or, rather, channel estimation, including techniques such as watermarking. The protection of both levels is necessary in order to provide assurance of the PVT, as both levels are used as input to the navigation function.
The mechanisms involved in the protection of the two layers are different and should incorporate distinct design drivers. Although it could be possible to use a single technique to protect both layers, this may result in sub-optimal performance. For instance, the adoption of NMA schemes can provide some assurance of ranging, based on the transmission of non-deterministic bit sequences. However, such protection is relatively weak when considered in the context of meaconing attacks employing early bit prediction or security code estimation and replay (SCER) techniques.
To improve the detection capability for such attacks, the number of unpredictable bits in the navigation message should be maximized. On the other hand, non-deterministic bit sequences can also have a negative impact on dissemination performance, particularly in challenging environments. Indeed, the navigation message is highly predictable for a given issue of data (IOD). Over time, receivers can accumulate the necessary pages of the navigation message containing ephemeris, clock correction terms, and so forth. With constantly changing bits of the message, the performance related to demodulation of authentication data are likely to degrade, affecting performance of NMA, including error rate and availability of authentication.
This paper follows a divide et impera approach, focusing only on providing an optimal solution for the protection of the data level. Ranging-level techniques will be discussed in a future article.
Design Drivers for NMA
Navigation message authentication seeks to authenticate for users the origin of navigation data and to provide cryptographic integrity protection for these. Navigation data is typically modulated on ranging signals at a low rate in order to minimize its effect on range estimation and provide adequate demodulation performance in a wide variety of environments for a message that changes infrequently.
For example, the data rate of the Galileo Open Service (OS) dissemination channel is 125bps; GPS C/A and L1C is 50 bps, the same bit-rate of the BeiDou D1 and GLONASS C/A signals. Therefore, NMA schemes must operate over a uni-directional broadcast channel and need to achieve an optimal tradeoff between the following factors:
- security — maximizing robustness against attacks, including
parameters such as size of keys, number of bits required for
authentication, security of algorithms, and security of key management
functions, such as key establishment - communications overhead — minimizing the bandwidth requirements of NMA, including the key management messages, e.g., renewal of the cryptographic keys
- robustness to channel errors — maximizing tolerance against errors in demodulation, especially in challenging environments
- tolerance for data loss — minimizing the consequences of losing authentication data on the continuity of operation, ability to recover from data loss
- scalability in terms of key management — suitability of the scheme for large groups of users, particularly in relation to distribution and management of keys.
- computation and memory requirements of the receiver — minimizing the burden of NMA processing on the receiver.
- Authentication performances — maximizing performance, including time to first authenticated fix (TTFAF) and authentication error rate (AER).
Authenticating information transmitted over wireless broadcast channels is a problem common to many telecommunications applications (e.g., broadcast television) and a variety of solutions, usually referred to as broadcast authentication, have been proposed. An extensive classification and comparison of such schemes can be found in the article by K. Grover and A. Lim cited in Additional Resources.
Digital signature (DS) schemes appear to be an obvious choice for NMA, due to the simplicity and scalability of key management that come with the use of asymmetric cryptography. The cryptographic community considers many DS schemes, such as those recommended by the European Network and Information Security Agency (ENISA), to be secure, and an additional number of DS methods are purported to be provably secure.
DS schemes often impose substantial overheads on the user in terms of computational complexity and the size of keys and/or signatures. An option for reducing this overhead is to use elliptic curve (EC) variants of the cryptographic primitives, which are able to reduce both the signature and key size. For example, the traditional digital signature algorithm (DSA) scheme requires a key of at least 1,024 bits, whereas an elliptical curve digital signature algorithm (ECDSA) requires a key size of just 160 bits for a security level of 80 bits. Both DSA schemes produce a signature of 320 bits; however, even 320 bits could be difficult to disseminate in highly bandwidth-constrained channels. For this reason, DS schemes are unlikely to be optimal for GNSS.
One-time signature schemes, including bins and balls (BiBa) and hash to obtain random subset (HORS) signatures, are a class of DSs offering the advantage of fast verification at the cost of increased memory requirements. As a drawback, they can only authenticate a preset number of messages before needing renewal of the public key. Therefore, the communication overhead and the public/private key size increase with the number of messages to be signed. For instance, as described in the article by A. A. Yavuz (Additional Resources), if HORS is used to sign 10,000 messages with an 80-bit security level, the required signature length is 200 bytes and the private and public key size are 24 and 48 megabytes, respectively.
Code-based signature methods, including McEliece or its Niederreiter variant based on Goppa codes and those based on low-density generator matrix (LDGM) codes, are a class of schemes against which all known attacks are still exponential. They present promising alternatives to public key schemes based on large number factorization, and are discrete logarithm problems, as they are believed to be secure against quantum computer attacks. Their security is based on the difficulty of some classical problems of coding theory, such as the well-known syndrome-decoding problem.
However, such methods have some non-negligible drawbacks concerning public key size, costs of signing and verification. In the article by N. Courtois et alia, the authors achieve good results in terms of signature length, that is, a 144 bits length for a security level equal to 80 bits. The signature length may also be shorter if traded off with the verification cost, while the public key size is still significant (1,152 kilobytes) in addition to the signature computation. Indeed, computing the latter signature will require between 10 and 30 seconds for a CPU frequency of one gigahertz.
The article by M. Baldi et alia (Additional Resources) addresses and improves the remedies for the last two problems, which for the same security level requires a public key of around 120 kilobytes. As regarding their application to NMA, it is worth considering these methods’ security robustness in order to be competitive over a longer time period. A more significant drawback of this class is the bandwidth requirement due to the large public key, which becomes almost impossible to renew over the air.
Traditional broadcast authentication schemes based on symmetric cryptography are prone to compromise, as users must share the same secret key as the system. The secret key is used for both generation of an authentication code and its verification. Users of such schemes must be trusted to not forge messages, or stringent security requirements are imposed on the receiver such that key storage and cryptographic processing take place within a tamper-resistant hardware module.
Other broadcast authentication schemes employing symmetric cryptography attempt to mitigate the risk associated with key compromise through a delayed key-disclosure paradigm. Each key used to generate an authentication code is disclosed to users after some delay, such that users only accept messages verified with the key if they have been received in a previous time window.
One such scheme is Timed Efficient Stream Loss-Tolerant Authentication (TESLA), an authentication protocol on which several NMA schemes proposed in the literature have been based. A distinctive characteristic of TESLA is the use of a one-way key chain as a basis for delayed key disclosure. Due to significant bandwidth limitations of the GNSS dissemination channel, many of the proposals for the application of TESLA in the GNSS context advocate the use of truncation to reduce the size of keys to be broadcast over the satellite channel.
NMA Methods Based on One-Way Functions
In this article, we discuss an alternative use of one-way chains in which digital signatures are amortized over a longer time period employing a one-way chain of message digests. This approach potentially provides benefits both in terms of bandwidth efficiency and security.
TESLA. As proposed in the article by A. Perrig (2000) et alia, this broadcast authentication protocol uses a delayed key disclosure scheme to provide authentication and cryptographic integrity protection of messages on a uni-directional broadcast channel.
The legitimate sender of a message using TESLA can compute a message authentication code (MAC) at transmission time, as the sender is the only entity with prior knowledge of the secret key. Once users have received a given message with the corresponding MAC, the sender can disclose the key allowing users to verify the previously received message.
The disclosed key needs to be authenticated, in turn, to ensure that both the key and message originated from the legitimate sender. This is typically achieved by verifying the key against a previously authenticated key, using iterations of one-way functions. These are functions that have the following properties:
- easy to compute — For any given input there exists an efficient method to compute the output.
- hard to invert — It is hard to find any input that generates a certain output. This is commonly referred to as pre-image resistance, when searching for the exact value, and second-preimage resistance when searching for any value different from the exact one that produces the same output value.
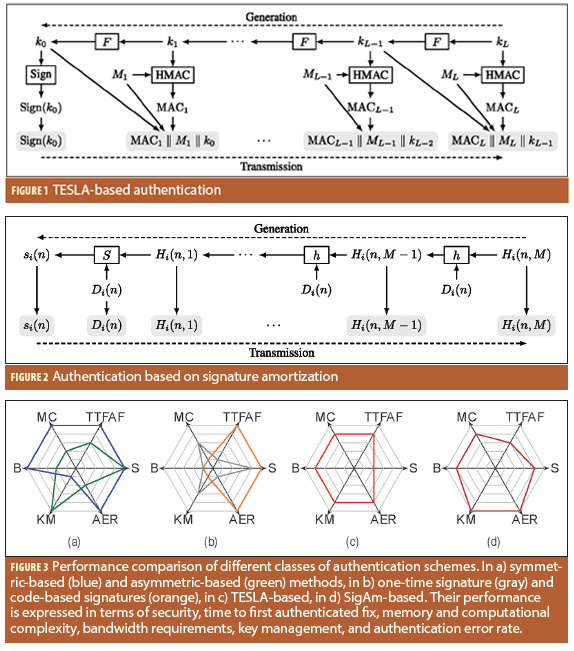
With TESLA, the sender generates a key-chain of length L by choosing a random secret (the first key), kL, and recursively applies a one-way function F(·), until the last key k0 (called the root key) is obtained. The generated key-chain is then used by the sender in the reverse order, as shown in Figure 1 (See inset photo, above right, for figures). Due to the one-way property of the chain, knowledge of key ki does not give any information on key ki+j ∀j > 0. The receiver is thus able to authenticate the key by applying the one-way function to the received key i times in order to recover the root key.
The root key must in turn be previously authenticated by other means, such as a digital signature. More generally, the verifier can stop applying the one-way function as it reaches a key that he has already authenticated, Fi-j(ki) = kj with j < i.
TESLA uses the keys from the key-chain for computing MACs. For instance, defining Mi the message that the transmitter wants to send at the time i, then by using the key ki, he computes MACi = S(Mi, ki) (where S is the authenticating algorithm), and sends a packet Pi =[Mi, MACi, ki-d], with d > 0.
The receiver is not able to verify the received packet Pi =[Mi, MACi, ki-d] instantaneously, because it does not know the value of ki used to compute MACi and, so, has to wait for its disclosure, after d steps. When the user receives the key k‘i he will first check if it is valid, and if the result is positive, he will compute the MAC for the received data with that key and check to determine if it is equal to the received one:
MACi = S(M‘i, k‘i) =? MAC‘i.
Various authors cited in Additional Resources have described different TESLA-based NMA schemes. The main differences of their relative work are:
- Key chain generation: In the paper by J. T. Curran et alia, the authors proposed to build the key chain and the authentication message as:
ki = trunc(hash(ki+1 ⊕ wpad ⎹⎸ GSTi), ℓkey) (1)
where wpad = 1010 … 10 is a 128-bit fixed sequence, ℓkey = 128 is the Galileo System Time, represents the length in bits of ki and trunc(x,y) denotes the truncation of x to its leftmost y bits.
In the paper by I. Fernández-Hernández et alia, the authors proposed to build the key chain as:
ki = trunc(hash(ki+1 ⎹⎸ α), ℓkey) (2)
where α is a binary sequence unique for every key chain that is disclosed at the beginning of the key chain, and ℓkey = 80 bits. Such construction was modified in the paper by P. Walker et alia with the inclusion of the GST in the computation:
ki = trunc(hash(ki+1 ⎹⎸ GSTi ⎹⎸ α), ℓkey) (3)
- Number of keys used: J. T. Curran et alia propose that all the space vehicles (SVs) use the same key and that a key is revealed every 30 seconds, allowing the verification of the corresponding MAC. I. Fernández-Hernández et alia and P. Walker et alia instead propose that every SV uses a different key, but all taken from the same key chain.
The latter concept assigns a new key to each SV so that for every authentication round each SV could broadcast a different key. This has the benefit of avoiding the possibility that an attacker could take advantage of the different propagation delays and replay the secret key from the SVs at the high elevation to the SVs at low elevation. To prevent this, in each round their scheme uses 40 keys from the same key chain.
On the other hand, these solutions exhibit some vulnerabilities, such as:
- Vulnerabilities to pre-computation attacks, in the case of I. Fernández-Hernández et alia where the padding is fixed for the whole chain length. This issue was fixed in the article by P. Walker et alia.
- Security of the key chain. The original TESLA scheme is considered secure, and various security proofs have been presented in the literature. A basic assumption in the security proofs is the time synchronization between transmitter and the receiver and the full entropy of each key, or at least that each key is the output of a pseudorandom function fed with a uniform input. However, in the repeated concatenation of many pseudorandom functions the key entropy will decrease, and the probability of collision will increase, in the end.
The article by G. Caparra (2016a) et alia shows that the probability of success of an attack that exploits collisions grows linearly with the length of the hash chain. Although in general this effect can be counteracted by the same probability decreasing exponentially with the key length, such a countermeasure may not be feasible when the key length is tightly constrained by the available system bandwidth. In this case the length of the chain should be appropriately limited.
Digital Signature Amortization. Digital signature amortization (SigAm) is a well-known concept originally designed for multicast applications over reliable channels. However, in its original form the technique cannot be readily applied to NMA for GNSS. Although some form of loss tolerance has been proposed e.g., Efficient Multi-chained Stream Signature (EMSS), it is not an intrinsic property of this scheme. Despite this, it is possible to exploit the structure of the slow-changing navigation message of GNSS to achieve loss tolerance.
The concept, as proposed by Y. Liu et alia (Additional Resources), is to authenticate a sequence of M messages using M
digests in a chained fashion so that each digest is authenticated by the previous one and only the first one is signed by some digital signature scheme. Although the use of a one-way chain is common to the TESLA scheme, the two solutions exploit it differently. TESLA uses a one-way chain to derive a set of keys where the current key is authenticated against previous ones, and uses keys from this chain to authenticate the navigation messages. In contrast, digital signature amortization SigAm makes use of the one-way chain in order to authenticate a longer message by a single digital signature, reducing the overhead required for authentication.
In order to achieve loss-tolerance, one can authenticate only those parts of the navigation message that do not change rapidly and use digest chains that last for the validity period, e.g., authenticate the ephemeris and clock correction data with a signature chain that last for the IOD duration. This will limit the AER because the navigation message, once correctly decoded, can be reused without requiring new demodulation. Furthermore, this implies that each navigation message is authenticated by means of a new DS, inheriting the security of the latter.
For a given time interval, the only authentication data that needs to be broadcast is the message digest. This is relatively short compared with a traditional digital signature for each message, or MACs and delayed keys in TESLA.
In order to allow a receiver that was unable to decode the signature of the root digest after the first transmission, either because the receiver was switched on after the beginning of the signature chain or due to decoding errors, the digital signature can be periodically broadcast, interleaved with the digests, in order to be able to authenticate the navigation message.
Figure 2 illustrates the SigAm concept. It’s easy to see the similarity with the TESLA one-way chain construction, with the difference that the navigation message is embedded in the computation of the chain itself.
As soon as the ephemerides that are to be broadcast are known, the SigAm authentication system can build the hash chain and the corresponding signature. First, it generates a random sequence of bits of the same length of the digest. Then, it starts the computation of the chain.
So, to implement the SigAm scheme, let i be the space vehicle (SV) index, n the chain index, and m the step index inside the chain. Let us define the hash function h as:
h(D, H) = trunc(SHA256(D ⎹⎸ H ⎹⎸ t), ℓH) (4)
where t, a time reference such as the Galileo System Time (GST) or the Z-count, is used as a counter to prevent pre-computation attacks and ℓH is the desired hash output length. The digest is recursively computed
as:
Hi(n, m) = h(Di(n) ⎹⎸ Hi(n, m + 1)), m = M – 1, … ,1
where Di(n) is the navigation data from SVi that we desire to protect, starting from the randomly generated Hi(n,M), with M being the length of the signature chain. When the last digest of the chain, Hi(n,1), is computed, the control center ends the procedure by computing the digital signature si(n).
The receiver first authenticates the navigation data Di(n) and first digest Hi(n,1) by verifying the received digital signature, si(n). If the latter is valid, Hi(n,1) is stored and will be compared with the one computed on the next received digest Hi(n,j), j = 1, … , M, which are received at subsequent rounds, up to the entire length of the chain.
To authenticate the subsequent message, a new chain of digests must be constructed and protected using another digital signature si(n + 1).
We can write the four operations as:
1. Signature:
Hi(n, M) ∼ U(ℋ), m=M
Hi(n, m) = h(Di(n), Hi(n, m + 1)), 1 ≤ m < M
si(n) = S(ki, [Di(n), ⎹⎸ Hi(n, 1)])
2. Transmission:
Hi(n) = [Hi(n, 1), Hi(n, 2), … , Hi(n, M)]
xi(n) = [Di(n), si(n), Hi(n)]
3. Reception:
x̂i(n) = [D̂i(n), ŝi(n), Ĥi(n)]
Ĥi(n) = [Ĥi(n, 1), Ĥi(n, 2), … , Ĥi(n, M)]
where the x̂i(·) notation accounts for possible forging attacks, illegitimate modifications or channel induced errors.
4. Verification: check if
u = V(Ki, [Di(n), ⎹⎸ Hi(n, 1) ⎹⎸ t], ŝi(n))
Ĥi(n, m – 1) = h(D̂i(n), Ĥi(n, m)), 2 ≤ m < M
Accept the signature if u otherwise reject.
Accept Ĥi(n, m) only if the applying the one-way function Ĥi(n, m – 1) is obtained.
As regards the signature algorithm, it could be any DS scheme, with elliptic curve variants to be preferred due to their shorter keys and signatures for the same level of security.
Taking the example of the Galileo E1B I/NAV message structure, we can conceive of the following dissemination strategy: In each I/NAV subframe the digital signature relative to the actual root digest is broadcast. The digital signature is divided into chunks (e.g., of 40 bits) and fitted over multiple pages.
The repetition at every subframe allows receivers in challenging environments to correctly accumulate all the chunks of digital signature independently. Moreover, in each subframe a new digest, computed using the TOW corresponding to the beginning of the first half page of the subframe, is transmitted. This will bring anti-replay protection capability at data level.
The digital signature uses around 240–320 bits and, assuming an 80-bit digest, this leads to a band requirement of around 400 bits for each subframe. If we can use more spare bits for the purpose of authentication, these bits can be used to improve the dissemination performance — introducing channel coding or disseminating information relatives to other SVs, or increasing the number of digest broadcast per subframe, if needed.
Moreover, the repetitions of predictable bits (after the first transmission) of the digital signature enable the receiver design to perform data wipeoff and use long coherent integration time, improving the tracking performance in the same way as can be done with the traditional navigation message. Thus, we should be able to find an optimal tradeoff between the repetitions of slow changing data (navigation message and digital signature) and fast changing data (digests).
Although the paper by G. Caparra (2016a) et alia (Additional Resources) shows that the use of padding-truncation in the construction of a one-way chain is not ideal, in this context we can use an 80-bit digest because the chain is short (assuming that it lasts only for the IOD duration) and the number of hash computed is small (i.e., two every minutes for less than two hours). This leads to a moderate reduction in the entropy of the chain (around seven bits) and to a reasonable increase of around two orders of magnitude of the collision probability (2 · 10−22 against 8 · 10−25), which is much smaller than the one faced by I. Fernández-Hernández et alia and P. Walker et alia.
Moreover, the design of SigAm limits the damage an attacker could cause to the users. Let’s consider the scenario in which an attacker manages to break the one-way chain. In TESLA the attacker will be able to generate a new navigation message with a correct MAC and have it accepted by the receiver. Thus, he will have the ability to change both the navigation message and the ranging. In comparison, with SigAm an attacker will only be able to change the ranging, by replaying the signal or even generating it in advance, but not to modify the navigation message, because a new navigation message requires a new digital signature.
Non-repudiation is the security service that prevents an entity from denying the generation of a message, and it is provided only by asymmetric cryptography. Indeed, in symmetric cryptography, the secret key is shared by both transmitter and receiver; thus, both can sign a message and claim that was originated by the other part. Instead, in the asymmetric paradigm, only the sender knows the private key able to compute the signature.
NMA can be the enabler for new location-based services, such as road tolling. In this context, it is likely that the attacker will not be a third party trying to guide the user in a wrong position, but the user him- or herself trying to pay less. The authentication provided by NMA can be used by the user to prove to the service provider that the reported PVT was computed using the navigation message broadcast by the system. Therefore, non-repudiation should be a feature of the authentication scheme.
In this case non-repudiation is not intended to prevent the system from repudiating a certain navigation message, but rather to prevent the computation of a valid signature by any other entity different from the system at any time. SigAm, just as with other digital signature–based NMA schemes, offers the non-repudiation service, while TESLA-based methods cannot, due to the use of symmetric cryptographic primitives to authenticate the navigation message.
Key Management
Cryptography can provide many features to a communication system, such as confidentiality, non-repudiation, integrity protection, and authentication. Every system making use of cryptography should support key management to regulate the use of cryptographic keys throughout their lifetime. In the design of an NMA scheme, the choice of parameters and the key management rules should aim at preserving confidentiality and authenticity of the secret keys, protecting them from unauthorized use.
A key generation algorithm should be carefully designed in order to ensure independence between the generated instances, that is, the leakage of a key shouldn’t compromise past or future keys. This is achieved by using fresh randomness for the generation of each new key, and it is vital for the system to keep such randomness secret.
One cryptographic best practice is to protect the keys by minimizing their cryptoperiod, the time during which a key is used before a new one is issued. A shorter cryptoperiod limits the amount of information that is protected by the same key, the time available for cryptanalytic attacks, and the exposure time of the system in case of key compromise.
Nevertheless, the frequency of key update affects communication overhead, since the system must broadcast key management messages. This tradeoff between bandwidth and security is a critical driver in the choice of a NMA scheme, as security needs to be maximized while taking into account the limitations of the application environment.
The key distribution mechanism should enable users to receive the keys with a reasonable delay with respect to the application and, at the same time, verify that the key has arrived unmodified from the intended source. A public key infrastructure can be used for this purpose. The system would use a private key to sign messages, which should be kept secret, whereas the corresponding public key can be published and used for verification.
Multiple asymmetric key pairs can be organized hierarchically: messages containing lower-layer keying material should be signed by the system with an upper-layer private key; in turn, when this key needs to be updated, a key from the external layer will be used. This key layering structure, creates a chain of trust: each layer inherits the trust from the layer above it; so, the external layer must be the strongest and most resistant to attacks.
This concept allows us to incorporate a key revocation mechanism. If a key is compromised, the system should have the possibility to prematurely end the lifetime of the current key. If the system detects such a situation, it should notify users of the corruption and revocation of the key. For this purpose, an alert message would be broadcast and a new key issued. Accordingly, the system should authenticate the new key with another previously established secret key from higher in the chain of trust.
The key management system might also offer additional services, such as a group management mechanism to take care of different user categories and a user revocation mechanism to allow the exclusion of subsets of users. The challenge is to provide a key management system that is able to integrate multiple services within its structure, accounting for diverse needs and service requirements.
As discussed earlier, revocation and renewal of asymmetric key pairs are fundamental functions in a key management system. NMA methods can reduce the risk of key compromise by introducing deterministic expiration times in order to limit the cryptoperiod. A separate problem is that of providing a method to revoke keys at random times, when there is evidence of key compromise. Straightforward solutions exist if we assume that users have access to the network, which becomes a challenge in the case of autonomous users, who rely on a uni-directional broadcast channel.
Comparison of Authentication Methods
Each of the schemes mentioned thus far provides a different tradeoff among the design drivers highlighted earlier. Figure 3 provides a pictorial representation of this tradeoff calculation.
In general, symmetric key–based schemes offer very good overall performance at the price of poor key-management scalability. This is a major issue that can be solved only by requiring tamper-resistant security modules (Figure 3a, in blue). If such devices are not an option, a different approach should be considered. Asymmetric key based schemes solve this issue providing an optimal solution in terms of key management and security, but reducing the performance in all the other requirements (Figure 3a, in green).
One time signatures can achieve good performance in terms of computational complexity, with no other outstanding point of merit, and they have major drawbacks in terms of memory and communication overhead (Figure 3b, in gray). Code-based signatures are believed to be secure against quantum computer attacks and can produce short digital signatures, but this approach requires very big public keys, which might render infeasible the over-the-air rekeying (OTAR) and require more storage space in the receiver (Figure 3b, in orange).
The performance of NMA schemes based on one-way chains lies in the middle ground of tradeoff benefits and drawbacks, achieving more balanced performance in all the requirements. The various adaptations of TESLA to GNSS achieve good overall performance, but they require us to trade security for communication overhead in a delicate design choice because optimal results cannot be achieved for both (Figure 3c). Rather than compromising on security to achieve desirable performance, SigAm could be a promising alternative, allowing gains in security and communication overhead at the cost of a longer TTFAF (Figure 3d).
Table 1 provides the rationale for the qualitative comparison.
Conclusion
This article introduced the design drivers for navigation message authentication for GNSS, highlighting the objectives that an NMA scheme must fulfill and discussing the different degrees of freedom that the system designers have in order to found the desired performance. The discussion moved to the analysis of candidate classes of cryptographic schemes that can be used to authenticate the navigation message, starting with the classical paradigms of symmetric and asymmetric authentication, continuing on to different solutions such as one-time signature, and ending with NMA schemes based on one-way chains.
These schemes are able to mix the advantages of both symmetric and asymmetric schemes. We presented two different ways to use one-way chains, TESLA and SigAm, which have different characteristics and potential tradeoffs. We can summarize the advantages of TESLA as the following:
- Fast first authenticated fix, because TESLA only needs a few bits (MAC+key) in addition to the current navigation data.
- Flexibility, as TESLA allows the authentication of any message, even if this changes rapidly and is not needed to be known in advance.
The benefits of SigAm are:
- Strong security, inherited from that of the signature scheme and not reduced significantly by the short hash chains.
- Small communication overhead, due to the lower number of bits needed to authenticate each message.
- No time synchronization is required for the security of the scheme.
- Immediate authentication, the receiver is able to verify the authenticity of the received message immediately after the reception.
Acknowledgments
The content of this article has been based on the analysis that has taken place under the activity funded by the European Space Agency, contract number 4000110548/14/NL/HK: “Advanced GNSS Open Service Signal Integrity Protection and Authentication at the Physical Layer” (A GOSSIP, A PLAY). The authors would like to acknowledge Dr. Massimo Crisci and Rigas T. Ioannides of TEC-ETN, ESA, ESTEC for their contributions and guidance throughout the activity.
Additional Resources
(1) Archer, M., “Proving Correctness of the Basic TESLA
Multicast Stream Authentication Protocol with TAME,” Workshop on Issues
in the Theory of Security(WITS ’02), Portland, Oregon, 2002
(2) Arze Pando, D. H., “Distance-Decreasing Attack in Global
Navigation Satellite System,” School of Computer and Communication
Sciences (I&C), Swiss Federal Institute of Technology (EPFL), 2009
(3) Baldi, M., and M. Bianchi, F. Chiaraluce, J. Rosenthal,
and D. Schipani, “Using LDGM Codes and Sparse Syndromes to Achieve
Digital Signatures,” in Post-Quantum Cryptography, PQ, pp. 1–15, Springer, Berlin-Heidelberg, Germany, May 2013
(4) Caparra, G., (2014), and N. Laurenti, R. T. Ioannides,
and M. Crisci, “Improved Secure Code Estimation and Replay Attack and
Detection on GNSS Signals,” in ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing, NAVITEC, 2014
(5) Caparra, G. (2016a), and S. Sturaro, N. Laurenti, and C.
Wullems, “Evaluating the Security of One-way Key Chains in TESLA-based
GNSS Navigation Message Authentication Schemes,” in ICL-GNSS 2016, Barcelona, Spain, 2016
(6) Caparra, G. (2016b), S. Sturaro, N. Laurenti, and C.
Wullems, “A Novel Navigation Message Authentication Scheme for GNSS Open
Service,” in ION GNSS+ 2016, (Portland, Oregon), 2016
(7) Courtois, N., and M. Finiasz and N. Sendrier, “How to Achieve a McEliece-Based Digital Signature Scheme,” in Advances in Cryptology – ASIACRYPT 2001 (C. Boyd, ed.), pp. 157–174, Springer, Berlin-Heidelberg, Germany, 2001
(8) Curran, J. T., and M. Paonni and J. Bishop, “Securing the
OpenService: A Candidate Navigation Message Authentication Scheme for
Galileo E1 OS,” in European Navigation Conference, (ENCGNSS), Rotterdam, Netherlands, 2014
(9) Fernández-Hernández, I., and V. Rijmen, G. Seco-Granados,
J. Simón, I. Rodríguez, and J. D. Calle, “Design Drivers, Solutions and
Robustness Assessment of Navigation Message Authentication for the
Galileo Open Service,” in Proceedings of the International Technical Meeting of The Satellite Division of the Institute of Navigation, ION GNSS, pp. 2810–2827, 2014
(10) Grover, K., and A. Lim, “A Survey of Broadcast Authentication Schemes for Wireless Networks,” Ad Hoc Networks, vol. 24, pp. 288–316, jan 2015
(11) Humphreys, T. E., “Detection Strategy for Cryptographic GNSS Anti-Spoofing,” IEEE Transactions on Aerospace and Electronic Systems, vol. 49, pp. 1073–1090, April 2013
(12) Ioannides, R., and T. Pany and G. Gibbons, “Known
Vulnerabilities of Global Navigation Satellite Systems, Status and
Potential Mitigation Techniques,” in Proceedings of the IEEE, Vol. 104, No. 6, June 2016
(13) Liu, Y., and J. Li and M. Guizani, “PKC Based Broadcast Authentication Using Signature Amortization for WSNs,” IEEE Transactions on Wireless Communications, vol. 11, pp. 2106–2115, June 2012
(14) Lomuscio, A., and B. Wozna, “A Complete and Decidable
Security-Specialised Logic and Its Application to the TESLA Protocol,”
in Proceedings of the Fifth International Joint Conference on Autonomous Agents and Multiagent Systems (AAMAS ’06), Hakodate, Hokkaido, Japan, ACM, 2006
(15) Ouranos, I., and K. Ogata and P. Stefaneas, “Formal Analysis of TESLA Protocol in the Timed OTS/CafeOBJ Method,” Lecture
Notes in Computer Science (including subseries Lecture Notes in
Artificial Intelligence and Lecture Notes in Bioinformatics), vol. 7610 LNCS, no. PART 2, pp. 126–142, 2012
(16) Perrig, A. (2000), and R. Canetti, J. Tygar, and D.
Song, “Efficient Authentication and Signing of Multicast Streams over
Lossy Channels,” in Proceeding 2000 IEEE Symposium on Security and Privacy, S&P 2000, pp. 56–73, IEEE Computer Society, 2000
(17) Perrig, A., (2001), “The BiBa One-Time Signature and Broadcast Authentication Protocol,” in Proceedings of the 8th ACM conference on Computer and Communications Security – CCS ’01, p. 28, ACM Press, November 2001
(18) Perrig, A., (2003) and J. D. Tygar, “Secure Broadcast Communication,” Wired and Wireless Networks, Springer, 2003
(19) Reyzin, L., and N. Reyzin, “Better than BiBa: Short One-Time Signatures with Fast Signing and Verifying,” in Information Security and Privacy, 7th Australasian Conference, ACISP 2002 (L. Batten and J. Seberry, eds.), pp. 144– 153, Springer-Verlag Heidelberg, Germany, 2002
(20) Smart, N. P., and V. Rijmen, B. Gierlichs, K. G.
Paterson, M. Stam, B. Warinschi, and G. Watson, “Algorithms, Key Size
and Protocols,” technical report, ENISA, 2014
(21) Walker, P., and V. Rijmen, I. Fernández-Hernández, G.
Seco-Granados, J. Simón, J. D. Calle, and O. Pozzobon, “Galileo Open
Service Authentication: A Complete Service Design and Provision
Analysis,” in ION GNSS+ 2015, Tampa, Florida, 2015
(22) Wullems, C., and O. Pozzobon and K. Kubik, “Signal
Authentication and Integrity Schemes for Next Generation Global
Navigation Satellite Systems,” in Proceedings of the European Navigation Conference, (ENC-GNSS), pp. 1–10, 2005
(23) Yavuz, A. A., “ETA: Efficient and Tiny and Authentication for hHterogeneous Wireless Systems,” in ACM conference on Wireless network security, WiSec, pp. 67–72, 2013
(24) Zhang, K. and P. Papadimitratos, “GNSS receiver tracking performance analysis under distance-decreasing attacks,” in IEEE International Conference on Location and GNSS, ICL-GNSS, pp. 1–6, IEEE, June 2015