In this article, we will take a look at the various GNSS signals from the perspective of their cost-benefit tradeoffs. First, we’ll look at the evolution of consumer GPS architecture to date — where acquisition speed and sensitivity have been the main drivers of receiver architecture. That architecture has evolved rapidly to take full advantage of the characteristics of the GPS C/A code.
In this article, we will take a look at the various GNSS signals from the perspective of their cost-benefit tradeoffs. First, we’ll look at the evolution of consumer GPS architecture to date — where acquisition speed and sensitivity have been the main drivers of receiver architecture. That architecture has evolved rapidly to take full advantage of the characteristics of the GPS C/A code.
Next, I want to explore the cost constraints of consumer GNSS. Then we’ll do a brief review of high-sensitivity issues before looking at the cost/benefits of new codes and higher data rates.
The theme that will emerge is that GPS L1 C/A code was designed almost perfectly for consumer GNSS. But, because engineers live to fix whatever they get their hands on, GNSS designers worldwide have been working tirelessly to “fix” GPS with more complex and longer codes and higher data rates. This is why the GPS C/A code will continue to be the most important signal for all consumer GNSS.
GNSS Market Segments
To provide focus for this article, we first need to identify GNSS applications by market segment.
There are military receivers and industrial receivers, which include survey (S), machine control (MC), timing (T), fleet management (F), aviation (A), and commercial marine (M). As shown in Figure 1, the total number of military and industrial receivers sold in 2012 was 4.5 million.
As for consumer products, we organize these into recreational, automotive, mobile computing, and mobile phone market segments.
Recreational receivers include cameras and fitness products, such as running watches, and approximately 25 million receivers were sold in 2012. Automotive receivers include embedded and after-market portable navigation devices (PNDs), with approximately half of the 45 million units being produced for each automotive receiver segment.
Finally, and not surprisingly, the largest segment includes mobile computing, tablets, and mobile phones. In 2012, there were 900 million mobile phones sold that incorporated GPS; to fit that to scale on the graph in Figure 2 would require it to be seven times wider.
This article focuses on L1-only receivers with assisted operation. These make up more than 90 percent of the total consumer market, including the entirety of the mobile computer, tablet, and cell phone segments and some of the automotive and recreational segments. Many automotive and recreational GNSS products are now similar to what we find in smartphones. For example, cameras and PNDs operate with Android OS and WiFi; consequently, these devices implement assisted-GNSS (A-GNSS).
Signal Processing Background
GNSS receiver architecture has evolved in the consumer market since the early days of GPS. Figure 3 depicts signal search that is needed to acquire each GPS signal. We need to search this space of code delay, 0-1023 chips on the x-axis and frequency offset on the y-axis.
The first important thing to note in the consumer market is that almost everything is assisted-GPS (A-GPS), and this helps us to considerably reduce the frequency search space, but not usually the delay space. This is because most cellular networks are not precisely time-synchronized. The CDMA network is synchronized with GPS, but other networks are typically time-accurate to only ±2 seconds.
Most LTE networks will also have this latter level of time accuracy; therefore, a consumer GPS receiver that needs to acquire a signal must search all the code-delay space for each frequency bin. It turns out that there is a great cost-benefit to searching this space as rapidly as possible, and receiver architecture has been driven by this fact.
Search Engine Evolution
A long, long time ago — way back in 1993 — receivers had just a few correlators. They searched one delay at a time, stored and accumulated the results, and if there was no energy, moved on. Acquisition of satellite signals was slow and only successful if the signals were strong (that is, users were outside and not under a tree).
Next came banks of correlators in modest numbers that provided benefits such as early-late tracking once the signal was found.
As A-GPS became the premier emerging technology for E-911, designers started using a large number of correlators, in earnest, with matched filter architecture that could search an entire code epoch in parallel. Note that the required memory size grows proportionally as we store all the possible hypotheses, because all are accumulated in parallel.
This approach was pioneered by Global Locate around 1999–2000, and now all consumer receivers have some form of massive parallel correlation, although these days most are implemented as shown in the final block diagram in Figure 4 — by using fast Fourier transform (FFT)/inverse FFT algorithms to implement the convolutions. This saves on total chip size, but memory remains the dominant factor in cost and size of mobile devices incorporating GNSS.
As we add correlators, we can obtain greater acquisition sensitivity for a given time-to-first-acquisition (TTFA), because as we increase the number of parallel searches, we can increase the integration time. This has a one-to-one effect on sensitivity, if we look at it as sensitivity in decibels vs. resources on a log scale, as shown in the figure. The horizontal axis shows the number of full code-epoch searches (this is the same as showing the number of correlators, but as we get to very large numbers of correlators it is more meaningful to discuss in terms of full code epochs).
Figure 5 includes four receivers spanning the last 20 years. With just a few correlators, which is where we were 20 years ago, we could search a few thousandths of a frequency bin. In the late 1990s, we could search a large fraction of a bin; and today, the receiver on one chip (Figure 6) can search more than 100 full bins in parallel.
Therefore, instead of spending time doing serial searches, a receiver can spend its entire time accumulating signals at every possible code-frequency hypothesis and achieve acquisition sensitivity of -156 dBm.
By the way, if we had done the same thing 20 years ago, when the industry was at the top-left data point on the curve in Figure 5, the chip would have had to increase by 10 iterations of Moore’s Law; that is, 210 or a thousand times bigger.
So, we see that there has been as rapid an evolution as possible to search the space defined by the 1023-chip GPS C/A code, because of this 1:1 cost-benefit curve.
A quick summary before we look at more modern signals:
- The cost benefit of adding search capability is good, and so today, most, if not all, consumer chips support massive parallel searches for all available GPS and GLONASS signals on L1.
- Memory now drives chip size (to store all those parallel hypotheses).
Now, when we read about modern GPS signals, we will often read that memory is very cheap today (thanks to Moore’s law), and this justifies longer codes. Well, let me give the consumer-market perspective on cost: the memory on a modern consumer GNSS chip is about 65 percent of the cost of a single- frequency L1 GNSS receiver chip, as shown in the pie chart in Figure 7.
Twenty years ago, if we had built that same chip, the memory would have been what? Still 65 percent of the cost of the chip. That is, memory isn’t any cheaper than anything else on the chip. The reason that almost a billion new GPS phones are sold each year is that the price of components is very competitive. We don’t necessarily get to say, “50 cents doesn’t sound like a large number to me; so, I’ll double up on memory size to accommodate a new long code.”
The cost itemization shown in Figure 8 is based on an analysis by iSuppli, a leading market research firm. It shows the estimated component costs of an iPhone 4. This was state-of-the-art two years ago; so, we might assume a 2x reduction on the same chips today.
Notice that most components in the phone cost around a dollar. Therefore, any manufacturer that changes its chip size and cost by, say, 50 cents, may suddenly find that its chips are 50 percent more expensive than those of competitors, and the benefit of that extra cost had better be pretty spectacular, or else they have just priced themselves out of the cell phone market.
Cost-Benefit Analysis
Let’s visit the GNSS system provider “zoo” for a cost-benefit analysis of the codes available to us on L1. Who is at the zoo in Figure 9? There’s the USA eagle’s GPS, Russian bear’s GLONASS, Chinese panda’s BeiDou, and European fox’s Galileo — each overseeing the signal components and associated performance of their respective GNSS systems.
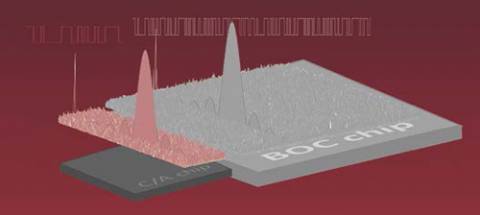
The longer the code, the more hypotheses we must store, if we want to do massive parallel searches. And so the search-RAM cost scales linearly with code length. Note that, because Galileo uses binary offset carrier (BOC) codes, a ¼-chip spacing is needed for search, which doubles the RAM required for storing search results. Consequently, instead of four times more memory than GPS (for the 4x longer code), it actually requires eight times more.
Some schemes have been proposed to use different chip spacing for BOC codes, reducing the RAM requirements back to about 4x GPS, but these may have an effect on performance. For the purpose of our analysis in this article, we’ll assume 1/4-chip spacing.
The main benefit of the longer codes is improved auto and cross-correlation properties. This is important to GNSS system designers who want to put all the different systems on the same frequency while affecting the noise floor as little as possible.
On the other hand, from the point of view of those billions of consumers, the best thing is to have shorter codes on different frequencies, which, for the moment, is available on GPS, GLONASS, and BeiDou. Because the cost of adding a different RF path is very small, designing the RF and front-end signal processing properly provides the benefit of jam immunity on any particular band.
Cross-correlation rejection is an issue with highly sensitive receivers. We can get spoofed by our own dynamic range when a satellite is blocked entirely and we “acquire” a cross correlation from a visible satellite with a strong signal. So, it is true that the longer codes will help prevent this, but actually the cross-correlation false-acquisition issue is much less of a problem in practice than we might think. We have other methods available to identify cross correlation, and the possible benefit of a longer code is actually quite small.
A related benefit associated with code rates also exists.
If the chip length is small, the correlation peak is sharper, which is analogous to GPS P-code, and provides more accuracy. With Galileo, although the chip length is the same as GPS, the PRN code is a BOC design. So, the latter signal’s correlation peak is not a simple triangle but rather a “W” with a sharper main peak than GPS. Thus, we expect similar accuracy for Galileo as we see for BeiDou.
This benefit of sharper peaks is actually quite dramatic, as we can see in Figure 10. The two plots in this figure show the GLONASS, GPS, and BeiDou (BDS) mean pseudorange residuals, which are post-fit residuals computed using known true positions. In other words, the plots show the mean error in the pseudorange measurements. The left plot shows measurements taken while driving in an urban environment, similar to San Francisco (but somewhere with more BeiDou satellites overhead). The right plot shows measurements taken while driving on rural freeways.
Notice how the errors are in the order that we would expect from the chip length. BeiDou has the shortest chip length, the sharpest correlation peaks, and the smallest errors. On the other hand, GLONASS has the longest chip length and the largest errors.
This is an interesting benefit of BeiDou and Galileo: we get better accuracy, especially with continuous tracking, but BeiDou and Galileo take a lot more memory to carry out their parallel searches.
In practice, what does this mean?
It means that we’ll still use all of these codes; it just doesn’t pay to build massive parallel search capability for all of them. Rather, it’s better to first search on GPS and GLONASS, acquire enough signals to set a local clock, and then do a fine-time narrow search for the longer codes of BeiDou and Galileo. In other words, we put the “A” back into C/A-code and use it for acquisition of longer codes, precisely as originally intended (only not for GPS P-code, but across different GNSS systems).
I hope you now start to see why I claim that GPS is the “Daddy” of GNSS. But you might be saying to yourself, “Hey, what about GLONASS — it requires even less search RAM — why isn’t GLONASS your Daddy?” After all, the GLONASS code length (511 chips) is half that of GPS (1023); so, receivers only have to store half as many search hypotheses when they are looking for the signal.
Well, it’s true that if all we wanted to do was minimize cost, regardless of accuracy and sensitivity, then GLONASS is actually the best choice, because it requires the least amount of RAM to conduct an acquisition search. However, in this article we are looking at the cost-benefit tradeoffs and, as we’ll see next, GLONASS takes us the wrong way on the cost-benefit curve. Furthermore, the operational performance of GPS makes it the most dependable of the GNSS systems so far — with few outages, reliable NANUs (Notice Advisories to Navstar Users) published in advance of any orbit or clock adjustments, and the best accuracy of the broadcast orbits. This performance, along with the signal-processing benefits, makes GPS a natural choice for a primary system.
Sensitive Matters
Let’s go a little deeper into high-sensitivity receiver operation by looking more closely at the effect of overlay codes and different data rates.
We should remember that the sensitivity that really matters to a consumer GNSS user is acquisition sensitivity, that is, how weak of a signal can we initially acquire?
The “show off” sensitivity numbers with which we might be familiar — for example, –160 and –170 dBm — are tracking- sensitivity specifications, and they have much less meaning in the real world, because tracking sensitivity only applies after a receiver has already acquired a signal — which is usually the more difficult phase. For many consumer applications, the GNSS feature turns on, gets a fix, and turns off; so, we don’t really care as much about tracking sensitivity. Also, tracking sensitivity doesn’t drive chip architecture, because once a receiver has acquired the signals, it needs very few correlators to continue to track them.
Acquisition sensitivity beyond -140 dBm is achieved with a combination of coherent and non-coherent integration. Also, for best sensitivity, the coherent integration time should be as long as possible, subject to the constraints imposed by the following:
- unknown changes in user motion
- unknown clock-frequency drift
- unknown bit transitions
Remember: before we have acquired signals, we usually don’t know the bit timing, even with A-GNSS, because typical time assistance is only good to about two seconds. Therefore, if we were to design a GNSS system optimally for consumer use, the best bit length would be somewhere in the range of 20 to 100 milliseconds. The longer the bit length, the more acquisition sensitivity we can get, but currently we’re practically limited towards the lower end, as explained next.
If we don’t know our velocity, then any coherent integration beyond 20 milliseconds doesn’t work (regardless of bit transitions), because any change in user velocity of one wavelength in 20 milliseconds will annihilate the coherent integration (as the phase changes). That is, with a moderate speed change of 20 mph (in the direction of the satellite) we could not do more than 20 milliseconds of coherent integration anyway.
With better integration of motion sensors, e.g., inertial measurement units, we can easily imagine that we might know velocity a priori. In that case, the receiver clock drift becomes the limiting factor, since our non-coherent integration will fail if the signal moves from one frequency bin to another during the noncoherent interval.
Frequency bins become proportionally narrower with increasing coherent interval: Doubling the coherent interval means halving the bin width. At 100-millisecond coherent interval the -3dB frequency bin roll-off is at ±3 ppb, which is narrow enough that a temperature controlled crystal oscillator (TCXO) could drift from one bin to another during the non-coherent interval — this is why 100 milliseconds is a natural upper limit.
In summary, if you were to build the perfect GNSS system for the consumer GNSS devices of today (which don’t have a priori velocity), we would want a data-bit length of exactly 20 milliseconds, which, of course, is exactly what we have with GPS.
Now we might say, “why do we need data bits at all if we have assisted-GPS?” We need them because our consumer GNSS receivers usually require precise time, because, as mentioned earlier, most cellular networks are not synchronized precisely. So A-GPS has an interesting relationship with data — we want it, but not too much of it.
Another Visit to the Zoo
With this discussion in mind, let’s go back to the GNSS zoo, where the various systems offer different bit rates and overlay codes (or “secondary codes”). From the point of view of coherent interval, an overlay code is similar to a data bit, as it limits our maximum coherent interval before we know the bit timing. Of course, the overlay codes are known; so, we could take advantage of that with much more memory.
For now, however, let’s consider any bit transition to be unknown, whether it’s a data bit or an overlay code transition. Then, if we limit ourselves to a two-decibel bit-alignment loss, we get the maximum coherent intervals shown in Figure 11. The way this works is that before we know the bit timing, we ignore bit transitions, integrate away, and “eat” the occasional loss from a bit transition, resulting in two decibels of energy loss with these coherent intervals.
Again GPS comes out ahead, unless we add more memory.
Now, here might be a good place to focus on the pilot signal of Galileo. Note that it has a 100-millisecond overlay code; so, it could (and probably will) give a significant benefit at some time in the future. But to take advantage of this code, we need significantly more search hypothesis memory (as already explained) and known a priori velocity, as discussed in the previous section.
Also, if we use only the Galileo pilot, we lose half the power. If we use both pilot and data, that increases the number of needed correlators and the related processing. This makes it harder for the theoretical advantage of the pilot code to become a practical reality in consumer products, and thus pushes the associated benefit further into the future.
Nonetheless, a really nice symmetry exists between the natural limits of 20 milliseconds and 100 milliseconds and the designs of the GNSS systems. It’s just that it will take several more iterations of Moore’s law to make this 100-millisecond code feasible as a search code for consumer products.
Putting all the above together, we can make a cost-benefit curve for some hypothetical GNSS chips. (See Figure 12.)
Imagine a single GNSS-system chip. The starting point is a GPS-only chip that would be approximately 2×2 millimeters to achieve -156 dBm acquisition sensitivity. The actual chip shown in Figure 6 is 2.0 x 2.4 millimeters, but it incorporates both GPS and GLONASS.
For this plot, assume that we make a GLONASS-only chip that takes advantage of the shorter GLONASS code. It would be smaller and cheaper than the GPS chip, but with loss of acquisition sensitivity because of the GLONASS overlay code of 10 milliseconds; so, it takes us backwards on the benefit curve.
BeiDou and Galileo each cost more to get the same sensitivity, because of their longer codes and higher data rates. Thus we see quite a different cost-benefit curve than the one we originally followed as GPS chips evolved from 20 years ago to now.
As previously mentioned, there is a point way out to the lower-right on the Sensitivity-Chip size curve, with a higher sensitivity that we can get to with a priori velocity and much greater memory, but that may be many years in the future.
Speaking of many years into the future — the L1C code will be on GPS III, with an operational constellation in about 10 years’ time. L1C will have an 18-second code. With enough search capability, we could find this signal and resolve the time ambiguity simultaneously (because assistance time is good to a couple of seconds). Therefore, benefits will certainly accrue to the new signals . . . eventually. But it may be a long time coming.
Summary
We’ve seen that acquisition sensitivity is the feature that drives consumer chip architecture and size; and this is primarily because of search memory. The GPS C/A code is a near-optimal signal for consumer products; any other single- constellation chip would either be less sensitive or more expensive. Future GNSS signals have attractive features (for example, Galileo and GPS III), but these are years away from providing a full benefit for acquisition sensitivity.
Thus, in the next several years I predict that we will see cell phones with: GPS+GLONASS chips (in fact, if you bought a smartphone in the last two years, you probably have this already).
We’ll also see:
- GPS + BeiDou
- GPS + GLONASS + BeiDou
- GPS + GLONASS + Galileo
- All of the above
But, what we will see very little of is a combination that excludes GPS.
Acknowledgment
This article is adapted from a keynote address by the author at the Stanford PNT (Position Navigation and Time) Symposium 2013, with invaluable contributions from John Betz, Charlie Abraham, Sergei Podshivalov, Andreas Warloe, and Javier de Salas.